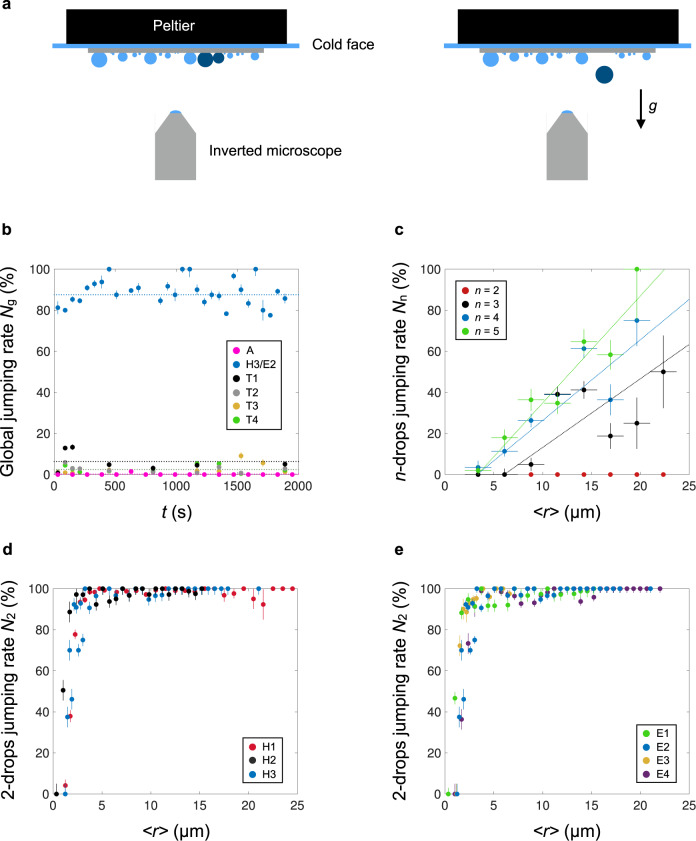
Fig. 4. Antifogging ability of nanocones.

a Schematic of the experiment: a sample is placed upside down on a Peltier cooler, which generates dew from atmospheric water. Droplets nucleate, grow and eventually coalesce, which we observe with an inverted optical microscope. We focus in particular on coalescing droplets (dark blue) and their possible takeoff from the material, from which we deduce the jumping rate of merging drops. b Global jumping rate N_g as a function of time t: we consider all observed coalescences and average the proportion N_g that results in droplet jumps after merging, over 1  min. For each series of data (obtained with pillar texture A, conical texture H3/E2 and truncated texture T1 to T4), we indicate with a dotted line the average value of N_g. The pink dots on the bottom show the jumping rate N_g = 0.2% for sample A. c Jumping rate N_n of droplets on truncated cones T1 as a function of the mean radius <r> of merging drops, after distinguishing the coalescences that imply n = 2, 3, 4, or 5 droplets. N_n increases with both n and <r>, explaining why a modest value of N_g can be accompanied by good antifogging abilities. Dotted lines are guides for the eyes. d, e. Jumping rate N₂ on sharp cones H/E for symmetric binary coalescences, for which merging radii do not differ by more than 20%. N₂ is plotted as a function of the average radius <r> for homothetic nanocones H1–H3 in d and for extruded cones E1–E4 in e. In both cases, the jumping rate plateaus at a constant value of 99 ± 1% above a critical radius r_c ≈ 1.5 ± 0.4 µm. Error bars represent the standard deviation of data.