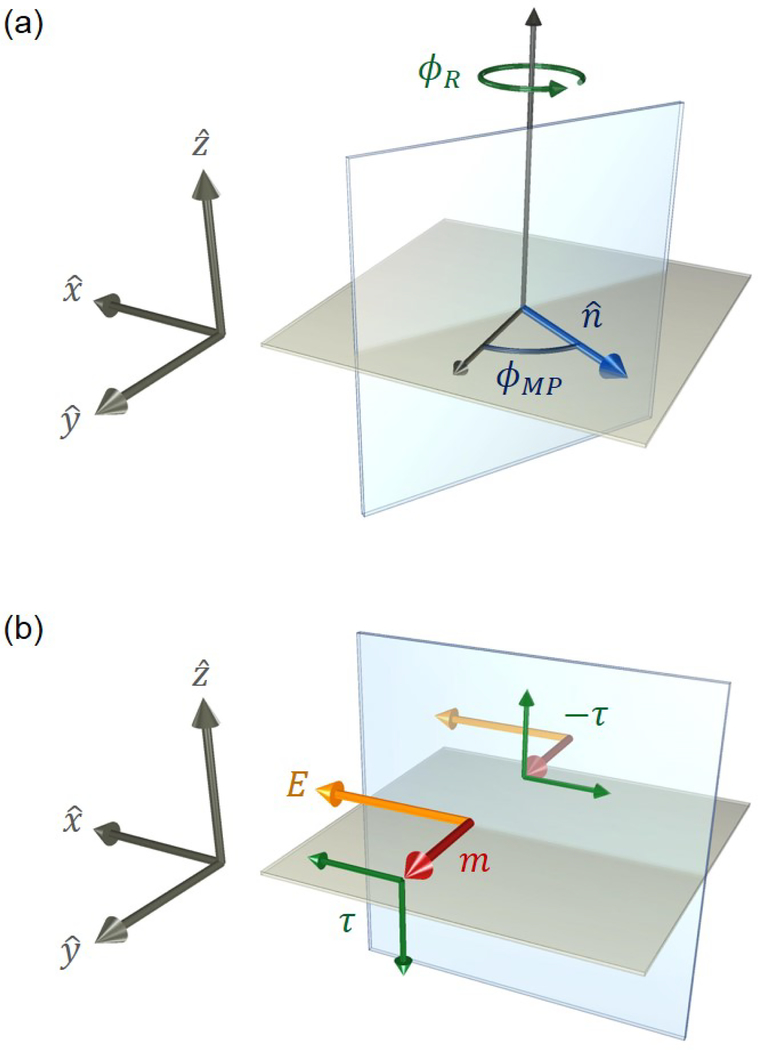
FIG. 8.
Depiction of symmetries and their consequences in a polycrystalline bilayer. (a) For nonmagnetic bilayers, any rotation φR about the out-of-plane direction (z-axis) leaves the system unchanged. Likewise, any mirror-plane transformation where the mirror-plane normal lies in-plane (parameterized by the angle 𝜙MP) also leaves the system invariant. (b) Under an applied, in-plane electric field E, all symmetries are broken except the mirror-plane that lies parallel to the electric field, since the electric field is a polar vector. If one layer is ferromagnetic, this symmetry is broken unless the magnetization points normal to the mirror-plane, since magnetization is a pseudovector. In this configuration, the torque τ must vanish, because a nonvanishing torque reflected through the mirror-plane will reverse, violating the system’s symmetry.