COVID-19 deaths in the USA: Benford’s law and under-reporting

Abstract

Background

I use Benford’s law to assess whether there is misreporting of coronavirus disease of 2019 (COVID-19) deaths in the USA.

Methods

I use three statistics to determine whether the reported deaths for US states are consistent with Benford’s law, where the probability of smaller digits is greater than the probability of larger digits.

Results

My findings indicate that there is under-reporting of COVID-19 deaths in the USA, although the evidence for and the extent of under-reporting does depend on the statistic one uses to assess conformity with Benford’s law.

Conclusions

Benford’s law is a useful diagnostic tool for verifying data and can be used before a more detailed audit or resource intensive investigation.

Introduction

The USA has suffered greatly during the coronavirus disease of 2019 (COVID-19) pandemic as it leads the world in total deaths from the virus.¹ The burden of death has also not been shared equally as the elderly and those with pre-existing medical conditions, particularly the residents of nursing homes, accounting for most of the deaths in the USA as well as elsewhere.²

Recently, the Attorney General of New York state released a report investigating the state’s nursing homes during the COVID-19 pandemic.³ The Attorney General’s investigation was prompted by allegations of neglect of nursing home residents during the pandemic and it found that the number of COVID-19 deaths that occurred in these homes was under-reported. The governor of New York later acknowledged under-reporting the number of deaths during the first wave of the pandemic for reasons that were motivated by political considerations.⁴

A statistical approach can also be used to verify the veracity of reported numbers. In particular, Benford’s law, which describes the distribution of digits, can be used to investigate whether the data are misreported by comparing the empirical distribution of digits with those predicted by Benford’s law. Benford’s law has been used to identify fraudulent or suspicious figures in many different settings: e.g. voting finance fraud; discrepancies in economic statistics; financial reports and other accounting information and, reports of COVID-19 cases.^5–12

I apply Benford’s law to the reported COVID-19 deaths in the USA by state to identify whether there is misreporting of deaths.

Data and methods

Benford’s law states that the distribution of (first) digits follows:

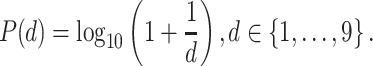(1)

Benford’s law means that the distribution of digits is not uniform with the probability of larger digits being lower than the probability of smaller digits. For example, the probability of a digit taking the value 1 is 0.301. In contrast, the probability of a digit taking the value 9 is 0.046. Deviations from the Benford distribution in Equation (1) can thus be used to identify fraudulent or altered figures.

I assess conformity with Benford’s law with three statistics. First, the goodness of fit (GF) test

(2)

where N is the number of observations, is the empirical frequency of digit d, 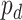is the frequency of digit d based on Benford’s law and 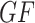has a Chi-squared distribution with 8 degrees of freedom. A limitation to the goodness of fit test is that it is dependent on the sample size, the mean absolute deviation (MAD) has been proposed as an alternative statistic to assess conformity to Benford’s law that is invariant to the sample size. ⁷ The MAD (for the first digit) is computed as

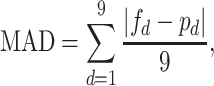(3)

and the notation is as defined earlier, where MAD values > 0.015 indicate nonconformity with Benford’s law, and MAD values < 0.015 show some sort of conformity. ⁷ Another useful statistic is the distortion factor (DF), which provides some indication of the over- or under-statement in the digits, by comparing the actual mean of the reported digits with the expected mean based on Benford’s law. ⁷ A negative DF suggests that an excess of lower first digits are used relative to what would be expected based on Benford’s law. The test statistic for the null hypothesis DF = 0 would have a standard normal distribution. ⁷

I use the data on COVID-19 deaths in the USA, which are available at the Centre for Disease Control (CDC) website.¹³ I use data for the 50 US states, New York City (NYC) and the District of Columbia (DC). I focus on the first wave of the pandemic identified in the New York Attorney General’s report as the period between 6 March 2020 and 5 August 2020 and assess whether the deaths reported in the US states, NYC and DC conform to Benford’s law based on the GF, MAD and DF statistics.

Results

I present the test statistics assessing conformity to Benford’s law in Table 1. The goodness of fit tests does not indicate a rejection of Benford’s law for NY and NYC. However, the MAD does indicate nonconformity with Benford’s Law for NY and NYC as they both have MADs that exceed 0.015. The distortion factors for NY and NYC suggest an excess of smaller digits, but I can only reject the null that the DF is nonzero for NY. This suggests that there is some conflict in these measures when determining if the data deviate from Benford’s law for NY and NYC. However, the MAD does clearly indicate that there were some deviations in the data from Benford’s law for both NY and NYC.

Table 1.

Assessing conformity with Benford’s law

State/district	GF {P- value}	MAD	Conformity	DF(× 100)	DF test
NY	7.039 {0.532}	0.021	NC	−14.06	−2.589
NYC	6.820 {0.556}	0.019	NC	−4.64	−0.822
AL	14.208 {0.076}	0.038	NC	−45.34	−7.878
AK	41.862{<0.001}	0.136	NC	—	—
AR	8.018 {0.432}	0.023	NC	−69.07	−11.806
AZ	4.764 {0.783}	0.014	MAC	−12.34	−2.213
CA	51.661{<0.001}	0.051	NC	30.86	5.801
CO	10.873 {0.209}	0.029	NC	−44.94	−7.935
CT	12.025 {0.150}	0.027	NC	10.94	1.917
DE	6.82 {0.556}	0.027	NC	−54.54	−8.416
DC	3.112 {0.927}	0.014	MAC	−64.58	−10.803
FL	46.262{<0.001}	0.040	NC	3.09	0.580
GA	20.680 {0.008}	0.040	NC	−8.62	−1.581
HI	29.61{<0.001}	0.115	NC	—	—
ID	16.983 {0.030}	0.046	NC	−64.21	−8.537
IL	8.922 {0.349}	0.024	NC	−2.36	−0.434
IN	4.250 {0.834}	0.016	NC	−28.96	−5.330
IA	7.589 {0.475}	0.023	NC	−65.28	−11.526
KS	3.249 {0.918}	0.017	NC	−65.06	−9.175
KY	23.421 {0.003}	0.040	NC	−68.93	−11.977
LA	6.510 {0.590}	0.019	NC	−17.23	−3.114
ME	31.626{<0.001}	0.070	NC	—	—
MD	12.737 {0.121}	0.028	NC	−12.42	−1.593
MA	14.962 {0.060}	0.033	NC	−16.24	−2.945
MI	10.630 {0.224}	0.020	NC	−10.66	−1.933
MN	9.874 {0.274}	0.022	NC	−35.42	−5.713
MS	12.180 {0.143}	0.031	NC	−44.61	−7.264
MO	39.883{<0.001}	0.057	NC	−58.04	−10.427
MT	27.617{<0.001}	0.084	NC	—	—
NE	22.132 {0.005}	0.048	NC	−67.80	−9.908
NV	13.748 {0.089}	0.034	NC	−54.03	−8.999
NH	2.083 {0.978}	0.011	AC	−69.33	−10.868
NJ	8.413 {0.394}	0.022	NC	−14.06	−2.606
NM	34.764{<0.001}	0.047	NC	−72.15	−12.688
NC	23.710 {0.003}	0.037	NC	−44.76	−8.089
ND	43.555{<0.001}	0.082	NC	—	—
OH	20.512 {0.009}	0.033	NC	−24.12	−4.408
OK	12.892 {0.116}	0.031	NC	−64.50	−10.355
OR	20.543 {0.009}	0.039	NC	−64.21	−10.647
PA	8.201 {0.414}	0.020	NC	−6.08	−1.073
RI	13.527 {0.095}	0.037	NC	−58.48	−9.478
SC	37.934{<0.001}	0.037	NC	−39.16	−7.207
SD	15.256 {0.054}	0.048	NC	—	—
TN	8.420 {0.394}	0.022	NC	−58.10	−10.259
TX	18.002 {0.021}	0.031	NC	−19.86	−3.655
UT	9.486 {0.303}	0.026	NC	−74.45	−11.896
VA	10.934 {0.205}	0.030	NC	−32.37	−5.647
VT	21.057 {0.007}	0.082	NC	—	—
WA	11.388 {0.181}	0.029	NC	−53.44	−10.278
WV	47.282{<0.001}	0.075	NC	—	—
WI	35.394{<0.001}	0.054	NC	−66.19	−11.455
WY	27.641{<0.001}	0.112	NC	—	—

Notes: P-value for GF test in braces; NC denotes nonconformity with Benford’s law, i.e. MAD >  0.015; AC denotes acceptable conformity with Benford’s law; MAC denotes marginal acceptable conformity with Benford’s law; — denotes DF is not computable. DF test has a standard normal distribution. Test statistics obtain using R package benford.analysis.

For the other US states and DC, the MAD indicates nonconformity in 47 states, with only 2 states and DC showing some sort of conformity. Compatibility with Benford’s law assessed with the goodness of fit test is much more variable. In particular, the GF test rejects conformity for 22 states at the 5% level of significance and 5 states at the 10% level.

The distortion factors for most US states and DC tend to indicate under-reporting of deaths (DF < 0), but there are three states with positive distortion factors. The distortion factor test rejects the null DF = 0 in 32 states and DC. In addition, with the exception of California, which has a positive DF statistic, these tests suggest that there are statistically significant under reports of COVID-19 deaths.

Discussion

Main findings of this study

The extent of compatible with Benford’s law does depend on the way it is tested, with the strongest and clearest evidence based on the MAD criteria. However, the results do indicate that there is evidence of under-reporting of COVID-19 deaths in the USA

What is already known on this topic?

Earlier papers have used Benford’s law to assess the validity of the reports of COVID-19 cases and deaths. ^8,9,11,12 Generally, conformity with Benford’s law tends to be in countries that are more developed and rank highly in democracy indexes. ¹¹

What this study adds

The result in this study point to the under-reporting of COVID-19 deaths in some US states as well as the usefulness of Benford’s law to assess the quality of epidemiological data. In addition, Benford’s law can be used as a preliminary diagnostic tool before a more detailed audit or verification study, which will require more resources.

Limitations

Applications of Benford’s law in finance and accounting tend to have much larger samples than are available in epidemiological data and this might explain some of the conflicting conclusions with different testing approaches.^7,8 Consequently, a lack of conformity with Benford’s law does not necessarily mean data are misreported or fraudulent.

Funding

This research did not receive any specific grant/financial support from funding agencies in the public, commercial or not-for-profit sectors.

Conflict of interest

None to report.

Data and code availability

Available at Harvard Dataverse https://doi.org/10.7910/DVN/NTJHMY.