FIG. 4.

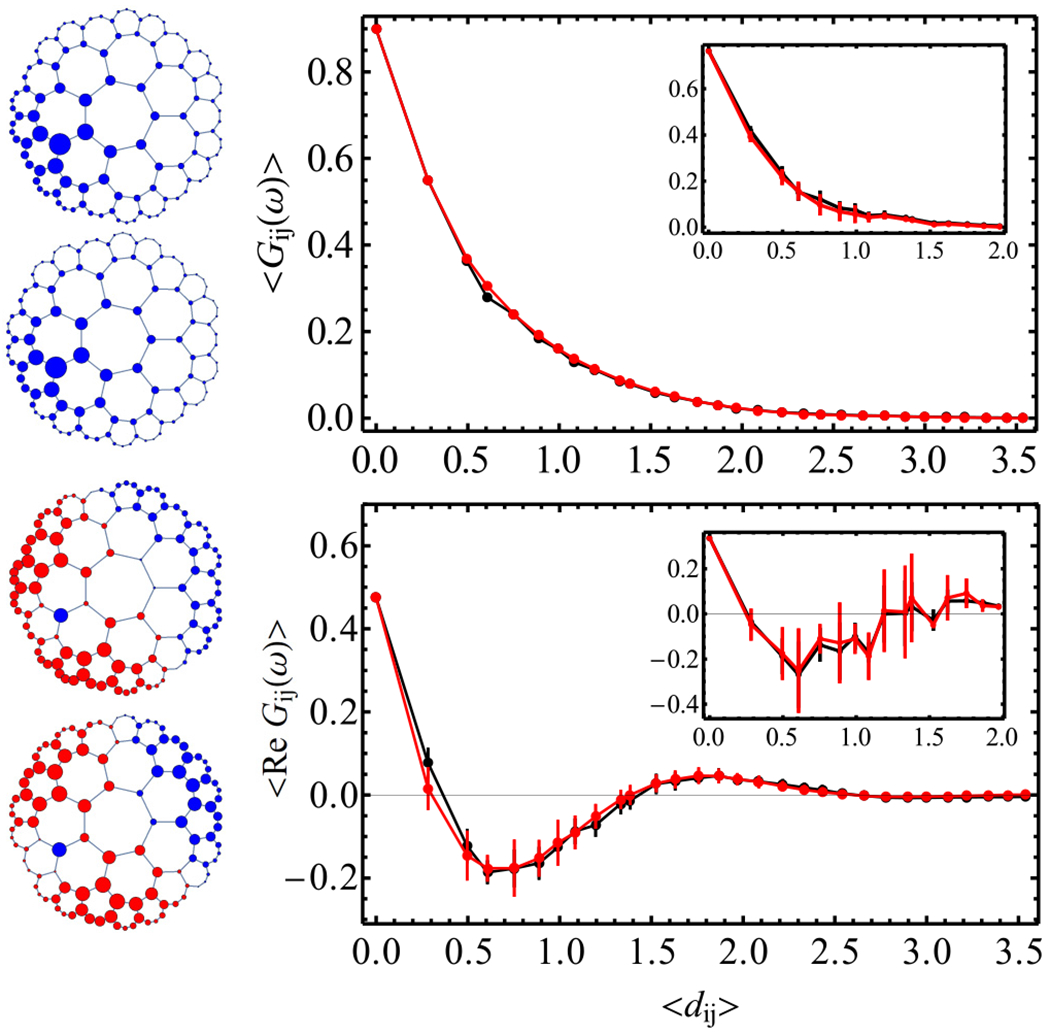
Quantitative match between graph Green function G_ij and continuum Green function G(z_i, z_j). We fix site z_i to be on the second ring, and plot the correlations as a function F_j of site z_j. Upper panel: Results for ω = −2.95 just below E₀. Left: The two plots are F_j = G_ij and F_j = G(z_i, z_j). The size of dots is proportional to |F_j|^1/2, and blue (red) corresponds to positive (negative) sign of F_j. Right: Mean correlation function vs hyperbolic distance d_ij = d(z_i, z_j), where the red (black) data are the graph (continuum) function. To obtain the curves, we make a list of pairs (F_j, d_ij) and compute the average F_j as a function of distance, with the error bar being the standard deviation. The quantitative agreement between graph and continuum is remarkable. Emergent conformal symmetry is reflected by the data points collapsing onto a single curve G_ij = f(d_ij) with some function f for large ℓ. The main plots are for ℓ = 6, the insets for ℓ = 3. Lower panel: The same setting for ω = −2.5 + 0.1i with Re(ω) > E₀. We plot the real part of the correlation function.