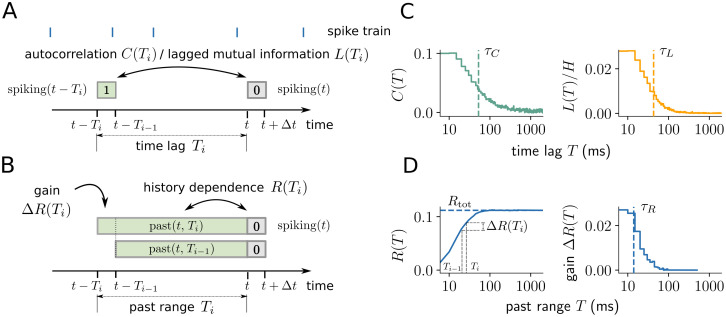
Fig 1. Illustration of history dependence and related measures in a neural spike train.

(A) For the analysis, spiking is represented by 0 or 1 in a small time bin Δt (grey box). Autocorrelation C(T_i) or the lagged mutual information L(T_i) quantify the statistical dependence of spiking on past spiking in a single past bin with time lag T_i (green box). (B) In contrast, history dependence R(T_i) quantifies the dependence of spiking on the entire spiking history in a past range T_i. The gain in history dependence ΔR(T_i) = R(T_i) − R(T_i−1) quantifies the increase in history dependence by increasing the past range from T_i−1 to T_i, and is defined in analogy to the lagged measures. (C) Autocorrelation C(T) and lagged mutual information L(T) for a typical example neuron (mouse, primary visual cortex). Both measures decay with increasing T, where L(T) decays slightly faster due to the non-linearity of the mutual information. Timescales τ_C and τ_L (vertical dashed lines) can be computed either by fitting an exponential decay (autocorrelation) or by using the generalized timescale (lagged mutual information). (D) In contrast, history dependence R(T) increases monotonically for systematically increasing past range T, until it saturates at the total history dependence R_tot. From R(T), the gain ΔR(T_i) can be computed between increasing past ranges T_i−1 and T_i (grey dashed lines). The gain ΔR(T) decays to zero like the time-lagged measures, with information timescale τ_R (dashed line).