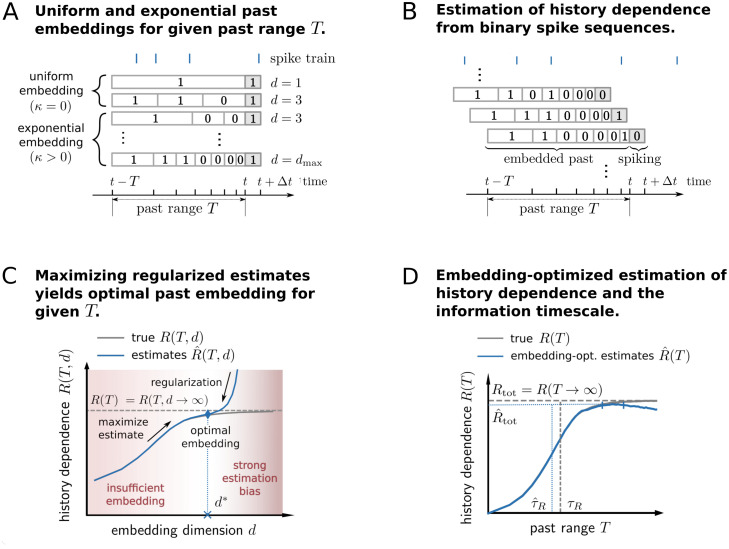
Fig 2. Illustration of embedding optimization to estimate history dependence and the information timescale.

(A) History dependence R is estimated from the observed joint statistics of current spiking in a small time bin [t + Δt) (dark grey) and the embedded past, i.e. a binary sequence representing past spiking in a past window [t − T, t). We systematically vary the number of bins d and bin sizes for fixed past range T. Bin sizes scale exponentially with bin index and a scaling exponent κ to reduce resolution for spikes farther into the past. (B) The joint statistics of current and past spiking are obtained by shifting the past range in steps of Δt and counting the resulting binary sequences. (C) Finding a good choice of embedding parameters (e.g. embedding dimension d) is challenging: When d is chosen too small, the true history dependence R(T) (dashed line) is not captured appropriately (insufficient embedding) and underestimated by estimates $\widehat{R}(T,d)$ (blue solid line). When d is chosen too high, estimates $\widehat{R}(T,d)$ are severely biased and R(T, d), as well as R(T), are overestimated (biased regime). Past-embedding optimization finds the optimal embedding parameter d* that maximizes the estimated history dependence $\widehat{R}(T,d)$ subject to regularization. This yields a best estimate $\widehat{R}\left(T\right)$ of R(T) (blue diamond). (D) Estimation of history dependence R(T) as a function of past range T. For each past range T, embedding parameters d and κ are optimized to yield an embedding-optimized estimate $\widehat{R}\left(T\right)$. From estimates $\widehat{R}\left(T\right)$, we obtain estimates ${\widehat{\tau }}_R$ and ${\widehat{R}}_{\text{tot}}$ of the information timescale τ_R and total history dependence R_tot (vertical and horizontal dashed lines). To compute ${\widehat{R}}_{\text{tot}}$ we average estimates $\widehat{R}\left(T\right)$ in an interval [T_D, T_max], for which estimates $\widehat{R}\left(T\right)$ reach a plateau (vertical blue bars, see Materials and methods). For high past ranges T, estimates $\widehat{R}\left(T\right)$ may decrease because a reliable estimation requires past embeddings with reduced temporal resolution.