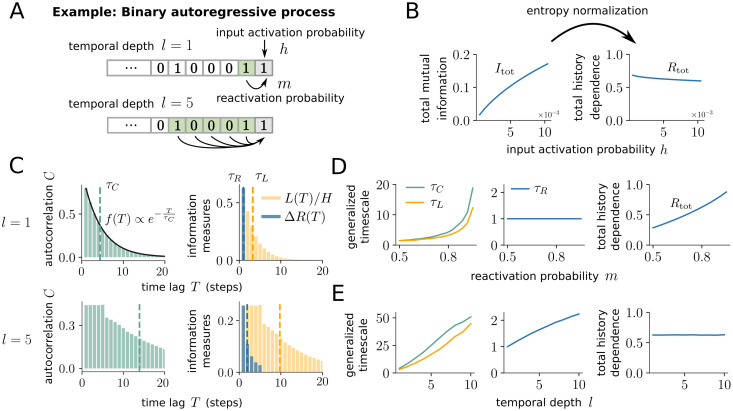
Fig 3. History dependence disentangles the effects of input activation, reactivation and temporal depth of a binary autoregressive process.

(A) In the binary autoregressive process, the state of the next time step (grey box) is active (one) either because of an input activation with probability h, or because of an internal reactivation. The internal activation is triggered by activity in the past l time steps (green), where each active state increases the activation probability by m. (B) Increasing the input activation probability h increases the total mutual information I_tot, although input activations are random and therefore not predictable. Normalizing the total mutual information by the entropy yields the total history dependence R_tot, which decreases mildly with h. (C) Autocorrelation C(T), lagged mutual information L(T) and gain in history dependence ΔR(T) decay differently with the time lag T. For l = 1 and m = 0.8 (top), autocorrelation C(T) decays exponentially with autocorrelation time τ_C, whereas L(T) decays faster due to the non-linearity of the mutual information. For l = 5 (bottom), C(T) and L(T) plateau over the temporal depth, and then decay much slower than for l = 1. In contrast, ΔR(T) is non-zero only for T shorter or equal to the temporal depth of the process, with much shorter timescale τ_R. Parameters m and h were adapted to match the firing rate and total history dependence between l = 1 and l = 5. (D) When increasing the reactivation probability m for l = 1, timescales of time-lagged measures τ_C and τ_L increase. For history dependence, the information timescale τ_R remains constant, but the total history dependence R_tot increases. (E) When varying the temporal depth l, all timescales increased. Parameters h and m were adapted to hold the firing rate and R_tot constant.