Abstract
The combination of multimodal imaging and genomics provides a more comprehensive way for the study of mental illnesses and brain functions. Deep network-based data fusion models have been developed to capture their complex associations, resulting in improved diagnosis of diseases. However, deep learning models are often difficult to interpret, bringing about challenges for uncovering biological mechanisms using these models. In this work, we develop an interpretable multimodal fusion model to perform automated diagnosis and result interpretation simultaneously. We name it Grad-CAM guided convolutional collaborative learning (gCAM-CCL), which is achieved by combining intermediate feature maps with gradient-based weights. The gCAM-CCL model can generate interpretable activation maps to quantify pixel-level contributions of the input features. Moreover, the estimated activation maps are class-specific, which can therefore facilitate the identification of biomarkers underlying different groups. We validate the gCAM-CCL model on a brain imaging-genetic study, and demonstrate its applications to both the classification of cognitive function groups and the discovery of underlying biological mechanisms. Specifically, our analysis results suggest that during task-fMRI scans, several object recognition related regions of interests (ROIs) are activated followed by several downstream encoding ROIs. In addition, the high cognitive group may have stronger neurotransmission signaling while the low cognitive group may have problems in brain/neuron development due to genetic variations.
Keywords: Interpretable, multimodal fusion, brain functional connectivity, CAM
I. Introduction
Recently, it is well recognized that multimodal imaging data fusion can exploit complementary information from multiple modalities, leading to more accurate diagnosis and discovery of underlying biological mechanisms [1]. Conventional multimodal fusion is often focused on matrix decomposition approaches. For example, canonical correlation analysis (CCA) [2] has been widely used to integrate multimodal data by detecting linear cross-modal correlations. To capture complex cross-modal associations, deep neural network (DNN) based models, e.g., deep CCA [3], were developed to extract high-level cross-modal associations. These methods can lead to improved performance in terms of prediction and diagnosis [3], [4].
Beyond diagnosis, it is also important to uncover biological mechanisms underlying mental disorders. This requires the data representation model to be interpretable. However, DNN is composed of a large number of layers and each layer consists of several nonlinear transforms/operations, e.g., nonlinear activation and convolution, causing difficulties in interpreting its representation. There have been many efforts to interpret DNN based models. Among these interpretation approaches, there typically exists a trade-off between “model performance”, “computational cost”, and “interpretability”. Simonyan et al. [5] proposed two methods: “class model visualization” to find the optimal image for the explanation of the trained model; and “class saliency visualization” to explain each image’s results. Perturbation-based methods [6] have also been proposed to evaluate each region/biomarker’s contribution by occluding it individually to see how much the classification accuracy is sacrificed as a result. Computational cost is however high because all voxels/biomarkers and their combinations are examined individually. Optimization-based methods obtain the occlusion by solving an optimization problem, i.e., minimizing the size of biomarkers and the loss of accuracy. For example, Fong et al. [7] proposed an optimization-based approach to only search for meaningful region candidates to reduce computational cost. In addition, Dabkowski et al. [8] developed a real-time interpretation framework but it introduced an additional network block; consequently, computationally intensive model-training is needed. There also have been some other optimization- or perturbation-based interpretation models [9], [10], but all of them introduce additional network training or additional optimization problems for each image input. Therefore, these approaches perform well for single image interpretation, but are impractical for large scale data analysis due to high computational costs.
To address this issue, we herein develop an interpretable DNN based multimodal fusion model, Grad-CAM guided convolutional collaborative learning (gCAM-CCL), which can perform automated diagnosis and result interpretation simultaneously. The gCAM-CCL model can generate interpretable activation maps indicating pixel-wise contributions of the inputs, enabling automated result interpretation. In particular, the activation maps are class-specific, which can reveal the underlying features or biomarkers specific to each class. In addition, gCAM-CCL can capture the cross-modal associations that are linked with phenotypical traits or disease conditions. This is achieved by feeding the network representations to a collaborative layer [11] which considers both cross-modal interactions and fitting to traits.
The contributions of our gCAM-CCL model are four-folds. First, it is a novel interpretable multimodal deep learning model, which can perform automated classification and interpretation simultaneously. Second, both cross-modal associations and the fitting to class-labels are considered using a batch-independent loss function, leading to better classification and association identification. Third, the interpretation is based on guided Grad-CAM, which allows for instant interpretation with high resolution class-specific activation maps. Fourth, we proposed an improved way of computing the weights for Grad-CAM, which focused on only the pixels with positive effects on class probabilities.
The rest of the paper is organized as follows. Section II introduces several related works and the limitations of existing multimodal fusion methods. Section III proposes our new model, gCAM-CCL, and describes how it overcomes the limitations. Section IV presents experimental results of applying gCAM-CCL to imaging genetic study. Section V concludes the work with a brief discussion.
II. Related works
A. Multimodal data fusion: analyzing cross-modal association
Classical multimodal data fusion methods are often focused on cross-modal matrix factorization. Among them, canonical correlation analysis (CCA) [2] has been widely used for multi-view/omics studies including our work [12]–[14]. CCA aims to find the most correlated variable pairs, i.e., canonical variables, and further association analysis can be performed accordingly.
Specifically, given two data matrices X1 ∈ ℝn×r, X2 ∈ ℝn×s (n represents sample/subject size, and r, s represents the feature/variable sizes in two data sets), CCA seeks two optimal loading vectors u1 ∈ ℝr×1 and u2 ∈ ℝs×1 which maximize the Pearson correlation corr(X1u1, X2u2), as in Eq. 1.
| (1) |
where 1, 2.
Solving the optimization in Eq. 1 yields the most correlated canonical variable pair, i.e., X1u1 and X2u2. More correlated canonical variable pairs (with lower correlations) can be obtained subsequently by solving the following extended optimization problem in Eq. 2.
| (2) |
where U1 ∈ ℝr×k, U2 ∈ ℝs×k, k = min(rank(X1), rank(X2)).
CCA captures only linear associations and therefore it requires that different data/views follow the same distribution. However, different modality data, e.g., fMRI imaging and genetic data, may follow different distributions and have different structures. As a result, CCA fails to detect the association between heterogeneous data sets. To address this problem, Deep CCA (DCCA) was proposed by Andrew et al. [3] to detect more complicated correlations. DCCA introduces a deep network representation before applying CCA framework. Unlike linear CCA, which finds the optimal canonical vectors u1, u2, DCCA seeks the optimal network representation f1(X1), f2(X2), as shown in Eq. 3.
| (3) |
where f1, f2 are two deep networks.
The introduction of deep network representation leads to a more flexible way to detect both linear and nonlinear correlations. According to the application to both speech and handwritten digits data analyses [3], DCCA was more effective in finding correlations compared to other methods, e.g., linear CCA, and kernel CCA. Despite DCCA’s superior performance, the detected associations may not be relevant to the phenotype of interest, e.g., disease. Instead, they may be caused by irrelevant signals, e.g., background and noise. As a result, they have limited value for identifying disease-related biomarkers.
B. Deep collaborative learning (DCL): phenotype-related cross-data association
To address the limitations of DCCA, we proposed a multimodal fusion model, deep collaborative learning (DCL) [11]. DCL can capture phenotype-related cross-modal associations by enforcing additional fitting to phenotype label, as formulated in Eq. 4.
| (4) |
where U1, U2 are subject to ; ; Z1 = f1(X1) ∈ ℝn×p, Z2 = f2(X2) ∈ ℝn×q; f1, f2 represent two deep networks, respectively; y ∈ ℝn×1 represents phenotype or label data; and a1, a2, a3 are the weight coefficients.
As shown in Eq. 4, DCL seeks the optimal network representation Z1 = f1(X1), Z2 = f2(X2) to maximize cross-modal correlations. Compared to DCCA, DCL’s representation retains label related information to guarantee that the identified associations are linked with label/phenotype. As a result, better classification of different cognitive groups can be achieved, according to the work described in [11]. Moreover, DCL relaxes the requirement that the projections u1 and u2 have to be in the same direction. This leads to an effective fitting to phenotypical information while incorporating cross-modal correlation.
With the ability to capture both cross-modal associations and trait-related features, DCL can combine complementary information from multimodal data, as demonstrated in our brain imaging study [11]. However, DCL uses deep networks to extract high-level features, which are difficult to interpret. As a result, DCL is limited by its ability for revealing disease mechanisms.
C. Deep Network Interpretation: CAM-based methods
Both DCCA and DCL use deep neural networks (DNN) for feature extraction. DNN employs a sequence of intermediate layers to extract high-level features. Each layer is composed of a number of complex operations, e.g., nonlinear activation, kernel convolution, batch normalization. DNN based models have found successful applications in both computer vision and medical imaging, due to their superior ability to extract high-level features. However, the large number of layers and the complex/nonlinear operations in each layer bring about a difficulty in network explanation and feature identification. Users may cast doubt on the reliability of the deep networks: whether deep networks make decisions based on the object of interest, or based on irrelevant/background information.
Optimization-based methods and perturbation-based methods have been proposed to partially interpret deep neural networks. However, both of them introduce additional optimization problems or network training for each image input, and consequently are computationally intensive and not appropriate for large scale applications.
1). Class Activation Mapping (CAM):
To make DNN explainable, Class Activation Mapping (CAM) method [15] was proposed. CAM generates an activation map for each sample/image indicating pixel-wise contributions to the decision, e.g., class label. Moreover, the activation maps are class-specific, providing more discriminative information for class-specific analysis. This dramatically helps build trust in deep networks: for correctly classified images/samples, CAM explains how the classification decision is made by highlighting the object of interest; for incorrectly classified images/samples, CAM illustrates the misleading regions.
The activation maps in CAM are obtained by computing an optimal combination of intermediate feature maps. A weight coefficient is needed for each feature map to evaluate its importance to the decision of interest. However, for most CNN-based models, this weight is not provided. To solve this problem, a re-training procedure is introduced, in which the feature maps are used directly by a newly introduced layer to re-conduct classification. The corresponding weights are then calculated using the parameters in the introduced layer. The detailed CAM method is described as follows.
For a pre-trained CNN-based model, assume that a target feature map layer consists of K channels/feature-maps Fk ∈ ℝh×w(k = 1, 2, · · ·, K), where h, w represent the height and width of each feature map, respectively. CAM discards all the subsequent layers and introduces a new layer (with softmax activation) to re-conduct classification using these feature maps Fk. Then a prediction score Sc is calculated by the newly introduced layer for each class c (c = 1, 2, · · ·, C), as formulated in Eq. 5.
| (5) |
where represents the weight coefficient of feature map Fk for class c.
After that, class-specific activation maps can be generated by first combining the feature maps with the trained weights followed by upsampling to project onto the input images, as in Eq. 6.
| (6) |
The re-training procedure, however, is time consuming, which limits CAM’s application. Moreover, classification accuracy sacrifices due to the modification of the model’s architecture.
2). Gradient-weighted CAM (Grad-CAM):
To address the limitation of the CAM method, Gradient-weighted CAM (Grad-CAM), was proposed [16] to compute activation maps without modifying the model’s architecture. Similar to CAM, Grad-CAM also needs a set of weight coefficients to combine feature maps. This can be achieved by first calculating the gradient of decision of interest w.r.t each feature map and then performing global average pooling on the gradients to get scalar weights. As a result, Grad-CAM avoids adding extra layers so both model-retraining and performance-decrease problems can be solved. The following is the description about how Grad-CAM calculates weights for the generation of activation map mapgradcam.
| (7) |
where yc represents the prediction score for class c, and
| (8) |
3). Guided Grad-CAM: high resolution class-specific activation maps:
Both CAM’s and Grad-CAM’s activation maps are coarse due to the upsampling procedure, as feature maps normally are of smaller size compared to input images. This brings about difficulties in identifying small but important features. Fine-grained visualization methods, e.g., guided back-propagation (BP) [17] and deconvolution [6], can generate high resolution activation maps. These methods use backward projections which operate on layer-to-layer gradients. Upsampling procedure is not involved in these back projection methods, and therefore high resolution activation maps can be obtained. Nevertheless, the activation maps are not class-specific, causing obstacles in interpreting the activation maps, especially for multiple classes. To obtain both high resolution and class-specific activation maps, guided Grad-CAM was proposed in the work [16] by incorporating guided BP into Grad-CAM. Guided Grad-CAM computes activation maps by performing a Hadamard product between the Grad-CAM map and the Guided BP map, as formulated in Eq. 9.
| (9) |
where mapguidedBP represents the map computed using guided BP algorithm [17], and ⊙ represents the Hadamard product operation. Given two arbitrary matrices A, B ∈ ℝm×n, their Hadamard product is defined as (A ⊙ B)ij := AijBij.
III. Grad-CAM guided convolutional collaborative learning (gCAM-CCL)
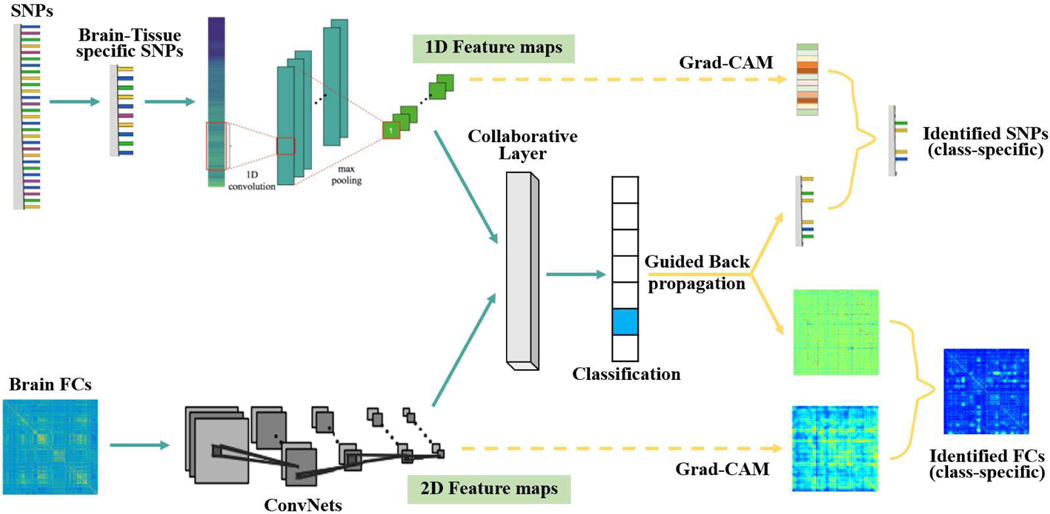
To this regard, we propose a new model, Grad-CAM guided convolutional collaborative learning (gCAM-CCL), which can perform automated multimodal fusion and result interpretation. As shown in Fig. 1, gCAM-CCL first integrates two modality data using the collaborative networks, and then computes class-specific activation maps using both Guided BP and Grad-CAM. As a result, gCAM-CCL can perform both classification and biomarker identification (i.e., result interpretation) simultaneously. Moreover, we propose an improved way to compute the weights for Grad-CAM, which can focus on only the pixels with positive effects on class probabilities.
Fig. 1:
The work-flow of grad-CAM guided convolutional collaborative learning (gCAM-CCL), an end-to-end model for automated classification and interpretation for multimodal data fusion. Genetic data is fed into a ConvNet and then flattened to a fully connected layer. Brain functional connectivity (FC) data is fed into a deep network. A collaborative learning layer fuses the two deep networks and passes two composite gradients mutually during the back-propagation process.
A. Proposed learning method
Compared to the DCL model [11], gCAM-CCL employs both a new architecture and a new loss function to incorporate Grad-CAM. Since computing activation maps needs a layer of feature-maps, gCAM-CCL replaces a multilayer perceptron (MLP) network with two ConvNets so that multi-channel feature maps can be obtained. This also benefits model-training because ConvNet dramatically reduces the number of parameters by enforcing shared kernel weights.
Moreover, as pointed out in Wang’s work [4], both DCCA [3] and DCL [11] include the parameter of sample size in their loss functions, giving rise to a problem of batch size tuning. In other words, the loss functions are dependent on batch size due to the correlation term at population-level. As a result, a large batch size is required [4] for network training. In this work, we propose a new loss function to relieve the issue of batch-size dependence, as formulated in Eq. 10. As shown in Eq. 10, the population-level correlation term is replaced with a summation of sample-level loss. Moreover, the correlation term is replaced with a regression loss, i.e., cross-entropy loss, since it has been shown that the optimization of correlation term is equivalent to the optimization of regression loss [4].
| (10) |
where , are the outputs of two ConvNets, as illustrated in Fig. 1.
This batch-independent loss function is easier to extend to multi-class and multi-view scenarios, where the extended loss function is given as follows.
| (11) |
where m represents the number of views, and C represents the number of classes.
B. Proposed interpretation method
The gCAM-CCL uses a 1D ConvNet to learn features from SNP data and uses a 2D ConvNet to learn features from brain imaging data, respectively. The output of two ConvNets are flattened and then fused in the collaborative layer with the loss function in Eq. 10, which considers both cross-modal associations and their fittings to phenotype/label y. After that, two intermediate layers are selected, from which the feature maps can be combined using the gradient-based weights (Eqs. 7–8) and class-specific Grad-CAM activation maps can be generated accordingly. Meanwhile, fine-grained activation maps are computed by projecting the gradients back from the collaborative layer to the input layer using Guided BP. The obtained activation maps indicate pixel-wise contributions to the decision of interest, e.g., prediction, and significant biomarkers, e.g., brain FCs and genes, can be identified accordingly.
Moreover, ideal class-specific activation maps should highlight only the features relevant to the corresponding class, e.g., ‘dog’ class. However, features related to other classes, e.g., fish-related features, may have negative contributions to predicting ‘dog’ class, resulting in noisy features in the activation maps. To remove the noisy or irrelevant features, we apply a ReLU function to the gradients, as shown in Eq. 12. The ReLU function ensures positive effects so that pixels with negative contributions can be filtered out.
| (12) |
where yc represents the prediction score for class c.
IV. Application to brain imaging genetic study
We apply the gCAM-CCL model to an imaging genetic study, in which brain FC data is integrated with single nucleotide polymorphism (SNPs) data to classify low/high cognitive groups. Multiple brain regions of interests (ROIs) function as a group when performing a specific task, e.g., reading. Brain FC depicts the functional associations between different brain ROIs [18]. On the other hand, genetic factors may also have influences on brain functions, as brain dysfunctionality is genetically inheritable. Imaging-genetic integration can probe brain function from a more comprehensive view, with the potential for revealing brain mechanisms. The proposed gCAM-CCL model will be used to extract and analyze complex interactions both within and between brain FC and genetics.
A. Brain imaging data
Several brain fMRI modalities from the Philadelphia Neurodevelopmental Cohort (PNC) [19] were used in the experiments. PNC cohort is a large-scale collaborative study between the Brain Behavior Laboratory at the University of Pennsylvania and the Children’s Hospital of Philadelphia. It has a collection of multiple neuroimaging data, e.g., fMRI, and genomic data, e.g., SNPs, collected from 854 adolescents aged from 8 to 21 years. Three types of fMRI data are available in PNC cohort: resting-state fMRI, emotion task fMRI, and nback task fMRI (nback-fMRI). As our work was focused on analyzing cognitive ability, only nback-fMRI, which was related to working memory and lexical processing, was used in the experiments. The duration of nback-fMRI scan was 11.6 minutes (231 TR), during which subjects were asked to conduct standard nback tasks.
SPM121 was used to conduct motion correction, spatial normalization, and spatial smoothing. Movement artifact (head motion effect) was removed via a regression procedure using a rigid body (6 parameters: 3 translation and 3 rotation parameters) [20], and the functional time series were band-pass filtered using a 0.01Hz to 0.1Hz frequency range as significant signals mainly focus on low frequency. For quality control, we excluded high motion subjects with translation > 2mm or with SFNR < 275 (Signal-to-fluctuation-noise ratio) following the work in [21]. 264 regions of interest (ROIs) (containing 21,384 voxels) were extracted based on the Power coordinates [22] with a sphere radius parameter of 5mm. For each subject, a 264 × 264 image was then obtained based on the 264 × 264 ROI-ROI connections, which was used next as image inputs for the gCAM-CCL model. The ROIs are arranged according to their spatial coordinates and their brain sub-networks information. The spatial information is based on the coordinates in the Montreal Neurological Institute space, and ROIs in the same brain sub-network are similar in terms of brain function. In this way, neighbor ROIs are both spatially and functionally close to each other.
B. SNP data
The genomic data were collected from 3 platforms, including the Illumina HumanHap 610 array, the Illumina HumanHap 500 array, and the Illumina Human Omni Express array. The three platforms generated 620k, 561k, 731k SNPs, respectively [19]. A common set of SNPs (313k) were extracted, and then PLINK [23] was used to perform standard quality controls, including the Hardy-Weinberg equilibrium test for genotyping errors with p-value < 1e−5, extraction of common SNPs (MAF > 5%), and linkage disequilibrium (LD) pruning with a threshold of 0.9. After that, SNPs with missing call rates > 10% and samples with missing SNPs > 5% were removed. The remaining missing values were imputed by Minimac 3 [24] using the reference genome from 1000 Genome Project. In addition, only the SNPs within gene bodies were kept for further analysis, resulting in 98,804 SNPs in 14,131 genes.
As the study aimed to investigate the brain, we further narrowed down to brain-expression-related SNPs. This was achieved using the expression quantitative trait loci (eQTL) data from Genotype-Tissue Expression (GTEx) 2 V7 database [25], a large scale consortium studying tissue-specific gene regulations and expressions. The GTEx data were collected from 53 different tissue sites from around 1000 subjects. Among the 53 tissue sites, 13 tissues were brain-related and they were listed in Table I. A set of 108 SNP loci were selected, which showed significant tissue regulation level (eQTL < 5×10e-8) in all 13 brain relevant tissues. In addition, SNPs in the top 100 brain-expressed genes were also selected based on the GTEx database. These procedures resulted in 750 SNP loci, which were used next as the genetic input to the gCAM-CCL model.
TABLE I:
13 Brain-related tissues from GTEx V7 database
| Tissue name | Sample size |
|---|---|
| Brain nucleus accumbens | 93 |
| Brain caudate | 100 |
| Brain cerebellar hemisphere | 89 |
| Brain cerebellum | 103 |
| Brain frontal cortex | 92 |
| Brain cortex | 96 |
| Brain amygdala | 76 |
| Brain spinal cord | 80 |
| Brain substantia nigra | 72 |
| Brain putamen | 82 |
| Brain anterior cingulate cortex | 72 |
| Brain hypothalamus | 81 |
| Brain hippocampus | 81 |
C. Integrating brain imaging and genetic data: classification
The gCAM-CCL was then applied to integrate brain imaging data with SNPs data to classify subjects with low/high cognitive functions. The wide range achievement test (WRAT) [26] score, a measure of comprehensive cognitive ability, including reading, comprehension, and math skills, was used to evaluate the cognitive level of each subject. The 854 subjects were divided into three classes: high cognitive/WRAT group (top 20% WRAT score), low cognitive/WRAT group (bottom 20% WRAT score), and middle group (the rest), following the procedures in the work [11].
The gCAM-CCL model adopted a 1D convolutional neural network (CNN) to learn the interactions between alleles at different SNP loci. ConvNet has been widely used for sequencing and gene expression data [27], [28] to learn local genetic structures. According to these studies, 1D kernels with relatively larger sizes are preferred. As a result, a 31×1 kernel and a 15 × 1 kernel were used. The detailed architecture of gCAM-CCL is listed in Table IV. The data is partitioned into training set (70%), validation set (15%), and test set (15%). The proposed gCAM-CCL model was trained on training set; hyper-parameters were selected based on the validation set; and the classification performance was reported based on the test set.
TABLE IV:
The Architecture of gCAM-CCL
| fMRI ConvNet | SNP ConvNet | ||||||
|---|---|---|---|---|---|---|---|
| Layer Name | Input Shape | Operations | Connects to | Layer Name | Input Shape | Operations | Connects to |
| f_conv1 | (b, 1, 264, 264) | K, P, MP = 7, 3, 2 | f_conv2 | s_conv1 | (b, 1, 750) | K, MP = 31, 6 | s_conv2 |
| f_conv2 | (b, 16, 132, 132) | K, P, MP = 5, 2, 4 | f_conv3 | s_conv2 | (b, 16, 120) | K, MP = 31, 6 | s_conv3 |
| f_conv3 | (b, 32, 33, 33) | K, P, MP = 3, 1, 3 | f_conv4 | s_conv3 | (b, 32, 15) | K = 15 | s_flatten |
| f_conv4 | (b, 32, 11, 11) | K = 11 | f_flatten | s_flatten | (b, 64, 1) | - | collab_layer |
| f_flatten | (b, 64, 1) | - | collab_layer | - | - | - | - |
| collab_layer | (b, 4) | ||||||
Notations: b (batch size), K (kernel size), P (padding), MP (maxpooling).
Hyper-parameters, including momentum, activation function, learning rate, decay rate, batch size, maximum epochs, were selected using the validation set and their values are listed in Table II. Mini-batch SGD was used to solve the optimization problem. Over-fitting problem occurred due to small sample size. To solve overfitting issue, a dropout was used and the dropout probability of the middle layers was set to be 0.2. Moreover, early stopping was used during network training to further overcome overfitting problem. In addition, batch normalization was implemented after each layer to relieve the gradient vanishing/exploding problem resulting from ReLU activation. Computational experiments were conducted on a Desktop with an Intel(R) Core(TM) i7–8700K CPU (@ 3.70GHz), a 16G RAM, and a NVIDIA GeForce GTX 1080 Ti GPU (11G).
TABLE II:
Hyper-parameter setting
| Methods | Epochs | batch size | Activation | Learning rate | Decay rate | dropout | Momentum |
|---|---|---|---|---|---|---|---|
| gCAM-CCL | 500 | 4 | ReLU, Sigmoid | 0.00001 | Half per 200 epochs | 0.2 (middle layers) | 0.9 |
To evaluate and compare the performance, several classical classifiers, e.g., SVM, random forest (RF), decision tree, were implemented for classifying low/high WRAT groups. In addition, several deep network based classifiers were implemented, including CCL with external classifiers (SVM/RF), and multilayer perceptron (MLP). Three multimodal-data-integration-based classifiers, i.e., gCAM-CCL, CCL+SVM, CCL+RF, take two omics data separately as the input, as shown in Fig. 1. In contrast, the other models take the concatenated data as the input. Specifically, to generate “concatenated data”, brain FCs were first flattened into vectors and then principal component analysis (PCA) was used for dimension reduction. After that, the brain FC vectors and SNPs vectors were concatenated as the “concatenated data”. We used radial basis function (RBF) kernel for SVM; and the RF classifier consists of 50 trees. The result of classifying high/low cognitive groups is shown in Table III. From Table III, the three data-integration-based classifiers outperform the concatenating classifiers. This is consistent with the result in our previous work [11], which also shows that the collaborative network with multimodal data can improve classification performance. Moreover, gCAM-CCL with intrinsic softmax classifiers achieves better classification compared with ‘CCL+SVM’ and ‘CCL+RF’. This may be due to the incorporation of cross-entropy loss in the model, i.e., Eq. 10, which facilitates the learning of loss-gradient during back-propagation process at each iteration.
TABLE III:
The comparison of classification performances (Low/High WRAT classification).
| Classifier | ACC | SEN | SPF | F1 |
|---|---|---|---|---|
| gCAM-CCL | 0.7501 | 0.7762 | 0.7157 | 0.7610 |
| CCL+SVM | 0.7387 | 0.7637 | 0.7083 | 0.7504 |
| CCL+RF | 0.7419 | 0.7666 | 0.7014 | 0.7523 |
| DCL+SVM | 0.7315 | 0.7578 | 0.6981 | 0.7354 |
| MLP | 0.7231 | 0.7555 | 0.6915 | 0.7215 |
| SVM | 0.7082 | 0.7562 | 0.6785 | 0.7093 |
| DT | 0.6626 | 0.6778 | 0.6430 | 0.6605 |
| RF | 0.7119 | 0.7559 | 0.6714 | 0.7138 |
| Logist | 0.6745 | 0.7386 | 0.6285 | 0.6900 |
D. Integrating brain imaging and genetic data: result interpretation
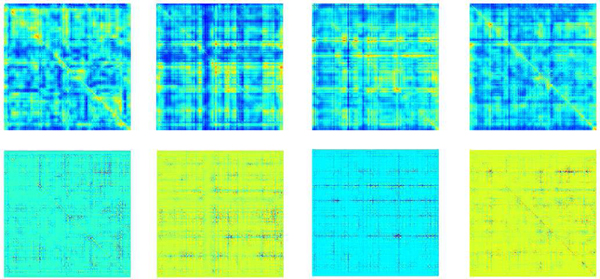
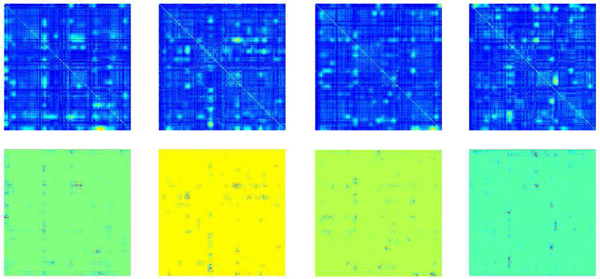
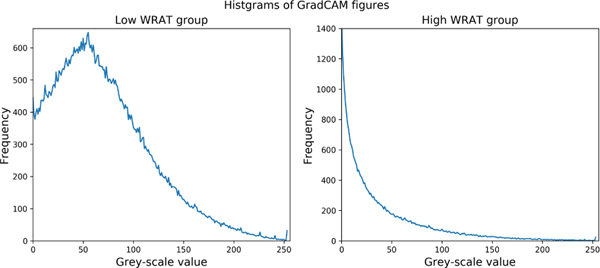
The class-specific activation maps for low WRAT group and high WRAT group were plotted in Figs. 2–3, respectively. From Fig. 2, the low WRAT group shows a relatively larger number of activated FCs, which contributed to the ‘low WRAT group’ class. In comparison, the high WRAT group (Fig. 3) has a relatively smaller number of significant FCs, which determined the ‘high WRAT group’ class. This is further validated in the average histogram of the activation maps, i.e., Fig. 4. For the low WRAT group (Fig. 4-left), a large portion of FCs were activated (high grey-scale value), while for the high WRAT group (Fig. 4-right), only a small portion of them were activated.
Fig. 2:
The brain FC activation maps for the Low WRAT group: Grad-CAM (top 4 subfigures) and Gradient-Guided Grad-CAM (bottom 4 subfigures).
Fig. 3:
The brain FC activation maps for the high WRAT group: Grad-CAM (top 4 subfigures) and Gradient-Guided Grad-CAM (bottom 4 subfigures).
Fig. 4:
The histogram of the Grad-CAM activation maps of brain FCs (see Figs. 2–3).
To identify significant brain FCs and SNPs, pixels with gray-value > 0.05×maximum gray-value were selected, following the instructions in the work [16]. After that, FCs and SNPs with > 0.7 occurring frequency across all subjects were further selected as significant FCs (see Figs. 5–6) and SNPs (listed in Tables V-VI).
Fig. 5:
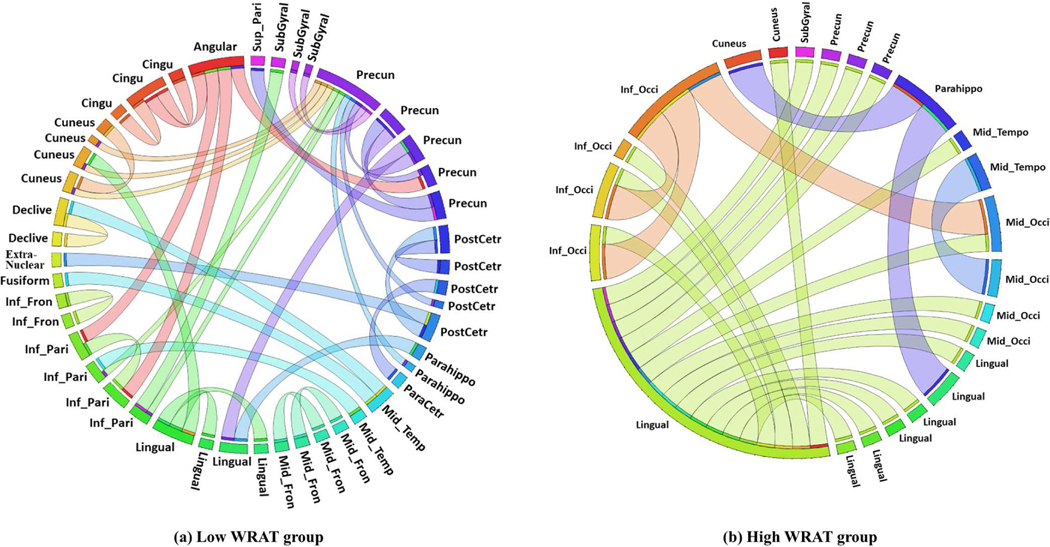
The identified class-discriminative brain FCs by gCAM-CCL. The full names of ROIs can be found in Table IX. Each circle arc represents an ROI (based on Power parcellation [22]). The length of a circle arc indicates the number of ROI-ROI connections for this ROI.
Fig. 6:
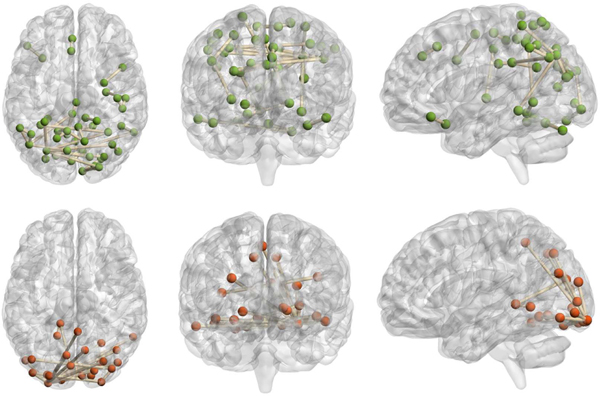
The identified brain functional connectivity. The top 3 subfigures: Low WRAT group (axial view, coronal view, sagittal view, respectively); the bottom 3 subfigures: High WRAT group (axial view, coronal view, sagittal view, respectively).
TABLE V:
Identified SNP loci (Low WRAT group)
| SNP rs # | Gene | SNP rs # | Gene |
|---|---|---|---|
| rs1642763 | ATP1B2 | rs997349 | MTURN |
| rs9508 | ATPIF1 | rs17547430 | MTURN |
| rs2242415 | BASP1 | rs7780166 | MTURN |
| rs11133892 | BASP1 | rs10488088 | MTURN |
| rs10113 | CALM3 | rs3750089 | MTURN |
| rs11136000 | CLU | rs2275007 | OSGEP |
| rs4963126 | DEAF1 | rs4849179 | PAX8 |
| rs11755449 | EEF1A1 | rs11539202 | PDHX |
| rs2073465 | EEF1A1 | rs1045288 | PSMD13 |
| rs1809148 | EEF1D | rs7563960 | RNASEH1 |
| rs4984683 | FBXL16 | rs145290 | RP1 |
| rs7026635 | FBXW2 | rs446227 | RP1 |
| rs734138 | FLYWCH1 | rs414352 | RP1 |
| rs2289681 | GFAP | rs6507920 | RPL17 |
| rs7258864 | GNG7 | rs12484030 | RPL3 |
| rs4807291 | GNG7 | rs10902222 | RPLP2 |
| rs887030 | GNG7 | rs8079544 | TP53 |
| rs7254861 | GNG7 | rs6726169 | TTL |
| rs12985186 | GNG7 | rs415430 | WNT3 |
| rs2070937 | HP | rs8078073 | YWHAE |
| rs622082 | IGHMBP2 | rs12452627 | YWHAE |
| rs12460 | LINS | rs324126 | ZNF880 |
| rs10044354 | LNPEP |
TABLE VI:
Identified SNP loci (High WRAT group)
| SNP rs # | Gene | SNP rs # | Gene |
|---|---|---|---|
| rs3787620 | APP | rs1056680 | MB |
| rs373521 | APP | rs9257936 | MOG |
| rs2829973 | APP | rs7660424 | MRFAP1 |
| rs1783016 | APP | rs3802577 | PHYH |
| rs440666 | APP | rs1414396 | PHYH |
| rs2753267 | ATP1A2 | rs1414395 | PHYH |
| rs10494336 | ATP1A2 | rs1037680 | PKM |
| rs1642763 | ATP1B2 | rs2329884 | PPM1F |
| rs10113 | CALM3 | rs1045288 | PSMD13 |
| rs2053053 | CAMK2A | rs2271882 | RAB3A |
| rs4958456 | CAMK2A | rs12294045 | SLC1A2 |
| rs4958445 | CAMK2A | rs3794089 | SLC1A2 |
| rs3756577 | CAMK2A | rs7102331 | SLC1A2 |
| rs874083 | CAMK2A | rs3798174 | SLC22A1 |
| rs3011928 | CAMTA1 | rs9457843 | SLC22A1 |
| rs890736 | CPLX2 | rs1443844 | SLC22A1 |
| rs17065524 | CPLX2 | rs6077693 | SNAP25 |
| rs12325282 | FAHD1 | rs363043 | SNAP25 |
| rs104664 | FAM118A | rs362569 | SNAP25 |
| rs6874 | FAM69B | rs10514299 | TMEM161B-AS1 |
| rs7026635 | FBXW2 | rs4717678 | TYW1B |
| rs12735664 | GLUL | rs8078073 | YWHAE |
| rs7155973 | HSP90AA1 | rs10521111 | YWHAE |
| rs2251110 | LOC101928134 | rs4790082 | YWHAE |
| rs2900856 | LOC441242 | rs10401135 | ZNF559 |
| rs8136867 | MAPK1 |
The identified brain FCs (ROI-ROI connections) and their corresponding ROIs were visualized in Fig. 5 and Fig. 6, respectively. For the high WRAT group (Fig. 5.b), three hub-ROIs (lingual gyrus, middle occipital gyrus, and inferior occipital gyrus) exhibited dominant ROI-ROI connections over the others. All of the three hub-ROIs are occipital-related. Lingual gyrus, also known as medial occipitotemporal gyrus, plays an important role in visual processing [29], [30], object recognition, and word processing [29]. The other two hubs, i.e., middle and inferior occipital gyrus, also play a role in object recognition [31]. As shown in Fig. 5.b, the hub-ROIs also connect to several other ROIs, e.g., cuneus, and parahippocampal gyrus. Among them, the cuneus receives visual signals and is involved in basic visual processing. The parahippocampal gyrus is related to encoding and recognition [32]. These suggest that the three occipital gyri are first activated when processing visual and word signals during the WRAT test, and then several downstream processing ROIs, e.g., para hippocampal gyrus, are activated for further complex encoding. As a result, strong FCs exist in these ROI-ROI connections, which may lead the gCAM-CCL to select the high WRAT group.
For the low WRAT group (Fig. 5.a), there were no significant hub ROIs identified. Instead, several previously reported task-negative regions, e.g., temporal-parietal and cingulate gyrus [33], were identified. This indicates that the low WRAT group may be weaker in activating cognition-processing ROIs and therefore task-negative are relatively more active, which may lead the gCAM-CCL to make the ‘low WRAT group’ decision.
As seen in Fig. 5a-b, a relatively larger number of FCs contributed to the low WRAT group, compared to that of the high WRAT group. Despite this, as shown in Table III, the sensitivity is lower than the specificity, which means that the accuracy of classifying low WRAT group is lower. This suggests that the identified FCs for the high WRAT group are relatively more discriminative and the low WRAT group may contain more noisy FCs.
Gene enrichment analysis is conducted on the identified SNPs (Tables V-VI) using ConsensusPathDB-human (CPDB) database3, and the enriched pathways are listed in Tables VII-VIII. Several neurotransmission related pathways, e.g., regulation of neurotransmitter levels and synaptic signaling, are enriched from the identified high WRAT group genes. This suggests that the high WRAT group may have stronger neuron signaling ability. The stronger neuron-signalling may benefit the daily training and development of ROI-ROI connections, which may therefore contribute to stronger cognitive ability. For the low WRAT group, several brain development and neuron growth related pathways, e.g., midbrain development and growth cone, are enriched, suggesting that the low WRAT group may have problems in brain/neuron development. This may further affect the ROI-ROI connections, leading to weaker cognitive ability. Therefore, the genetic differences may lead to differences in ROI-ROI connection, and especially the visual processing and information encoding ROIs; and may further contribute to the differences in the brain FC patterns between the two cognition groups. As a result, subjects with both neuro-transmission-related genetic biomarkers and the image-processing-related brain FCs may lead classifiers to more likely make the ‘high cognition’ decision. In contrast, subjects with both neuron-underdevelopment-related biomarkers and weaker image-processing-related FC patterns may lead to a higher score on the “low cognition” class.
TABLE VII:
Gene enrichment analysis of the identified genes (Low WRAT group). Q-values represent multiple testing corrected p-value.
| Pathway Name | Pathway Source | Set size | Contained | p-value | q-value |
|---|---|---|---|---|---|
| Eukaryotic Translation Elongation | Reactome | 106 | 5 | 1.18E-06 | 1.65E-05 |
| Peptide chain elongation | Reactome | 101 | 4 | 3.12E-05 | 2.18E-04 |
| Calcium Regulation in the Cardiac Cell | Wikipathways | 149 | 4 | 1.48E-04 | 6.89E-04 |
| Translation | Reactome | 310 | 5 | 2.09E-04 | 7.33E-04 |
| Metabolism of proteins | Reactome | 2008 | 11 | 3.96E-04 | 1.11E-03 |
| Midbrain development | Gene Ontology | 94 | 4 | 1.22E-05 | 1.53E-03 |
| Site of polarized growth | Gene Ontology | 167 | 4 | 1.25E-04 | 2.19E-03 |
| Growth cone | Gene Ontology | 165 | 4 | 1.20E-04 | 4.07E-03 |
| Cellular catabolic process | Gene Ontology | 2260 | 12 | 7.22E-05 | 4.55E-03 |
| Pathways in cancer - Homo sapiens (human) | KEGG | 526 | 5 | 2.39E-03 | 5.58E-03 |
| Metabolism of amino acids and derivatives | Reactome | 342 | 4 | 3.20E-03 | 6.40E-03 |
TABLE VIII:
Gene enrichment analysis of the identified genes (High WRAT group). Q-values represent multiple testing corrected p-values.
| Pathway Name | Pathway Source | Set size | Contained | p-value | q-value |
|---|---|---|---|---|---|
| Regulation of neurotransmitter levels | Gene Ontology | 335 | 9 | 6.77E-10 | 1.04E-07 |
| Transmission across Chemical Synapses | Reactome | 224 | 7 | 7.75E-08 | 2.40E-06 |
| Synaptic signaling | Gene Ontology | 711 | 10 | 3.17E-08 | 2.43E-06 |
| Insulin secretion - Homo sapiens (human) | KEGG | 85 | 5 | 3.26E-07 | 5.06E-06 |
| Organelle localization by membrane tethering | Gene Ontology | 170 | 6 | 1.34E-07 | 6.84E-06 |
| Regulation of synaptic plasticity | Gene Ontology | 179 | 6 | 1.89E-07 | 7.21E-06 |
| Exocytosis | Gene Ontology | 909 | 10 | 3.06E-07 | 9.36E-06 |
| Membrane docking | Gene Ontology | 179 | 6 | 1.82E-07 | 1.28E-05 |
| Vesicle docking involved in exocytosis | Gene Ontology | 45 | 4 | 5.11E-07 | 1.30E-05 |
| Plasma membrane bounded cell projection part | Gene Ontology | 1452 | 12 | 3.05E-07 | 1.34E-05 |
| Cell projection part | Gene Ontology | 1452 | 12 | 3.05E-07 | 1.37E-05 |
| Neurotransmitter release cycle | Reactome | 51 | 4 | 1.76E-06 | 1.37E-05 |
| Synaptic Vesicle Pathway | Wikipathways | 51 | 4 | 1.76E-06 | 1.37E-05 |
| Neuronal System | Reactome | 368 | 7 | 2.25E-06 | 1.39E-05 |
| Secretion by cell | Gene Ontology | 1493 | 12 | 4.13E-07 | 1.45E-05 |
| Adrenergic signaling in cardiomyocytes - Homo sapiens (human) | KEGG | 144 | 5 | 4.47E-06 | 2.31E-05 |
| Gastric acid secretion - Homo sapiens (human) | KEGG | 75 | 4 | 8.34E-06 | 3.70E-05 |
| Neuron part | Gene Ontology | 1713 | 12 | 1.83E-06 | 4.09E-05 |
| Plasma membrane bounded cell projection | Gene Ontology | 2098 | 13 | 2.22E-06 | 4.87E-05 |
V. Conclusion
In this work, we proposed an interpretable multimodal deep learning based fusion model, namely gCAM-CCL, which can perform both classification and result interpretation. The gCAM-CCL model generates activation maps to display pixel-wise contribution of input images and genetic vectors. Specifically, it calculates each feature map’s gradients and then merges the gradients with global average pooling to combine the feature maps. Moreover, the activation maps are class-specific, which further promotes class-difference analysis with potential discovery of biological mechanisms.
The proposed model was applied to an imaging-genetic study to classify low/high WRAT groups. Experimental results demonstrate gCAM-CCL’s superior performance in both classification and biological mechanism analysis. Based on the generated activation maps, a number of significant brain FCs and SNPs were identified. Among the significant FCs (ROI-ROI connections), three visual processing ROIs exhibited dominant ROI-ROI connections over the others. In addition, several signal encoding ROIs, e.g., the parahippocampa gyrus, showed connections to the three hub-ROIs. These suggest that during task-fMRI scans, object recognition related ROIs are first activated and then downstream ROIs get involved with signal encoding. Results also suggest that high cognitive group may have higher neuron-transmitter signalling levels while low cognitive group may have problems in brain/neuron development, due to genetic-level differences. In summary, gCAM-CCL has demonstrated superior classification accuracy than several competitive models, in addition to being able to identify significant biomarkers. Besides the proposed imaging-genetic study, the model is generic, which can find widespread applications in multimodal data integration.
TABLE IX:
Abbreviations of the ROIs
| Inferior Parietal Lobule (Inf_Pari) | Angular Gyrus (Angular) |
| Inferior Occipital Gyrus (Inf_Occi) | Fusiform Gyrus (fusiform) |
| Inferior Frontal Gyrus (Inf_Fron) | Cingulate Gyrus (Cingu) |
| Middle Occipital Gyrus (Mid_Occi) | Sub-Gyral (SubGyral) |
| Middle Frontal Gyrus (Mid_Fron) | Paracentral Lobule (ParaCetr) |
| Parahippocampa Gyrus (Parahippo) | Postcentral Gyrus (PostCetr) |
| Middle Temporal Gyrus (Mid_Temp) | Precuneus (Precun) |
| Superior Parietal Lobule (Sup_Pari) | Lingual gyrus (Lingual) |
Acknowledgments
This work was partially supported by the NIH (R01 GM109068, R01 MH104680, R01 MH107354, P20 GM103472, R01 EB020407, R01 EB006841, R01 MH121101, R01 DA047828) and NSF (#1539067).
Footnotes
Contributor Information
Wenxing Hu, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118..
Xianghe Meng, Center of System Biology, Data Information and Re-productive Health, School of Basic Medical Science, Central South University, Changsha, Hunan, 410008, China..
Yuntong Bai, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118..
Aiying Zhang, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118..
Gang Qu, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118..
Biao Cai, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118..
Gemeng Zhang, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118..
Tony W. Wilson, Institute for Human Neuroscience, Boys Town National Research Hospital, Boys Town, NE 68101.
Julia M. Stephen, Mind Research Network, Albuquerque, NM 87106.
Vince D. Calhoun, Tri-institutional Center for Translational Research in Neuroimaging and Data Science (TReNDS), Georgia State University, Georgia Institute of Technology, Emory University, Atlanta, GA 30030..
Yu-Ping Wang, Biomedical Engineering Department, Tulane University, New Orleans, LA 70118..
References
- [1].Sui J. et al. , “Neuroimaging-based individualized prediction of cognition and behavior for mental disorders and health: Methods and promises,” Biological Psychiatry, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Hotelling H, “Relations between two sets of variates,” Biometrika, vol. 28, pp. 321–377, 1936. [Google Scholar]
- [3].Andrew G. et al. , “Deep canonical correlation analysis,” in International Conference on Machine Learning, 2013, pp. 1247–1255. [Google Scholar]
- [4].Wang W. et al. , “On deep multi-view representation learning,” in International Conference on Machine Learning, 2015, pp. 1083–1092. [Google Scholar]
- [5].Simonyan K. et al. , “Deep inside convolutional networks: Visualising image classification models and saliency maps,” 2014. [Google Scholar]
- [6].Zeiler MD and Fergus R, “Visualizing and understanding convolutional networks,” in European conference on computer vision. Springer, 2014, pp. 818–833. [Google Scholar]
- [7].Fong RC and Vedaldi A, “Interpretable explanations of black boxes by meaningful perturbation,” in Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 3429–3437. [Google Scholar]
- [8].Dabkowski P. and Gal Y, “Real time image saliency for black box classifiers,” in Advances in Neural Information Processing Systems, 2017, pp. 6967–6976. [Google Scholar]
- [9].Yuan H. et al. , “Interpreting deep models for text analysis via optimization and regularization methods,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, 2019, pp. 5717–5724. [Google Scholar]
- [10].Fong R. et al. , “Understanding deep networks via extremal perturbations and smooth masks,” in Proceedings of the IEEE International Conference on Computer Vision, 2019, pp. 2950–2958. [Google Scholar]
- [11].Hu W. et al. , “Deep collaborative learning with application to multimodal brain development study,” IEEE Transactions on Biomedical Engineering, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Hu W, “Adaptive sparse multiple canonical correlation analysis with application to imaging (epi) genomics study of schizophrenia,” IEEE Transactions on Biomedical Engineering, vol. 65, no. 2, pp. 390–399, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Lin D. et al. , “Correspondence between fmri and snp data by group sparse canonical correlation analysis,” Medical image analysis, vol. 18, no. 6, pp. 891–902, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hu W. et al. , “Integration of snps-fmri-methylation data with sparse multi-cca for schizophrenia study,” in 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE, 2016, pp. 3310–3313. [DOI] [PubMed] [Google Scholar]
- [15].Zhou B. et al. , “Learning deep features for discriminative localization,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 2921–2929. [Google Scholar]
- [16].Selvaraju RR et al. , “Grad-cam: Visual explanations from deep networks via gradient-based localization,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 618–626. [Google Scholar]
- [17].Springenberg JT et al. , “Striving for simplicity: The all convolutional net,” arXiv preprint arXiv:1412.6806, 2014. [Google Scholar]
- [18].Calhoun VD and Adali T, “Time-varying brain connectivity in fmri data: whole-brain data-driven approaches for capturing and characterizing dynamic states,” IEEE Signal Processing Magazine, vol. 33, no. 3, pp. 52–66, 2016. [Google Scholar]
- [19].Satterthwaite TD et al. , “Neuroimaging of the philadelphia neurodevelopmental cohort,” Neuroimage, vol. 86, pp. 544–553, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Friston KJ et al. , “Characterizing dynamic brain responses with fmri: a multivariate approach,” Neuroimage, vol. 2, no. 2, pp. 166–172, 1995. [DOI] [PubMed] [Google Scholar]
- [21].Rashid B. et al. , “Dynamic connectivity states estimated from resting fmri identify differences among schizophrenia, bipolar disorder, and healthy control subjects,” Frontiers in human neuroscience, vol. 8, p. 897, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Power JD et al. , “Functional network organization of the human brain,” Neuron, vol. 72, no. 4, pp. 665–678, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Purcell S. et al. , “Plink: a tool set for whole-genome association and population-based linkage analyses,” The American journal of human genetics, vol. 81, no. 3, pp. 559–575, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Das S. et al. , “Next-generation genotype imputation service and methods,” Nature genetics, vol. 48, no. 10, p. 1284, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Lonsdale J. et al. , “The genotype-tissue expression (gtex) project,” Nature genetics, vol. 45, no. 6, p. 580, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Wilkinson GS and Robertson GJ, Wide range achievement test. Psychological Assessment Resources, 2006. [Google Scholar]
- [27].Singh R. et al. , “Deepchrome: deep-learning for predicting gene expression from histone modifications,” Bioinformatics, vol. 32, no. 17, pp. i639–i648, 2016. [DOI] [PubMed] [Google Scholar]
- [28].Zhou J. et al. , “Deep learning sequence-based ab initio prediction of variant effects on expression and disease risk,” Nature genetics, vol. 50, no. 8, p. 1171, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Mechelli A. et al. , “Differential effects of word length and visual contrast in the fusiform and lingual gyri during,” Proceedings of the Royal Society of London. Series B: Biological Sciences, vol. 267, no. 1455, pp. 1909–1913, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Mangun GR et al. , “Erp and fmri measures of visual spatial selective attention,” Human brain mapping, vol. 6, no. 5–6, pp. 383–389, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Grill-Spector K. et al. , “The lateral occipital complex and its role in object recognition,” Vision research, vol. 41, no. 10–11, pp. 1409–1422, 2001. [DOI] [PubMed] [Google Scholar]
- [32].Mégevand P. et al. , “Seeing scenes: topographic visual hallucinations evoked by direct electrical stimulation of the parahippocampal place area,” Journal of Neuroscience, vol. 34, no. 16, pp. 5399–5405, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Hamilton JP et al. , “Default-mode and task-positive network activity in major depressive disorder: implications for adaptive and maladaptive rumination,” Biological psychiatry, vol. 70, no. 4, pp. 327–333, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]