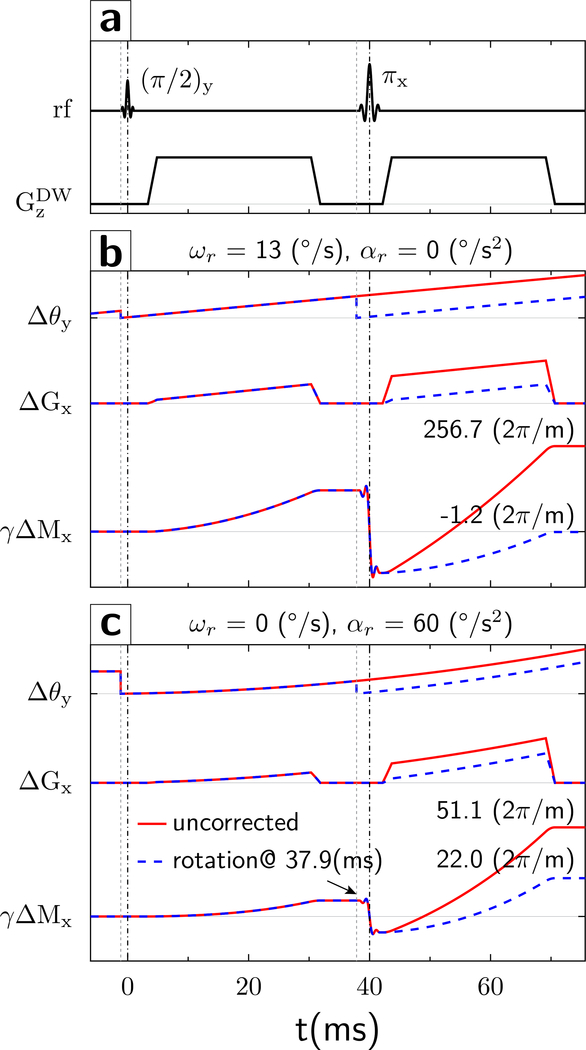
Figure 2:

Evolution of gradient waveforms (a) and gradient moments. (b) For a y-rotational motion with constant angular velocity of ω_r = 13°/s (no acceleration) relative to the stationary diffusion gradient in z-direction (Δθ), the spins experience an effective x-gradient (ΔG_x) that continues to increase throughout the experiment. Thus, a non-zero gradient moment starts to build up quadratically in the first TE/2 period (γΔM_x, solid red line). The refocusing pulse reverses the gradient moment at TE/2. Without an additional motion update, the gradient moment continues to accumulate rapidly (γΔM_x solid red line) and reaches a non-zero value at TE. However, if the rotation matrix is updated prior to the refocusing pulse, then the axis of the object is re-aligned with the gradient axis (Δθ, dashed blue line). This results in a final residual gradient moment γΔM_x that is markedly smaller (γΔM_x, dashed blue line) compared to that obtained without the additional motion update (γΔM_x, solid red line). (c) Rotational motion with constant rotational acceleration of ${\propto }_{\mathrm{r}}=60°/{\mathrm{s}}^2$ (0 constant velocity). The overall evolution of the gradient moment is similar to that described in (b) but follows a third-order term in time. Again, without an intra-sequence motion update, the gradient moment continues to accumulate rapidly in the second TE/2 period (γΔM_x, solid red line) and reaches a non-zero value at TE. If the rotation matrix is updated prior to the refocusing pulse, the final residual gradient moment is smaller (γΔM_x, dashed blue line) compared to that obtained without the additional motion update (γΔM_x, solid red line) but still deviates from zero due to the third-order evolution of the gradient moment.