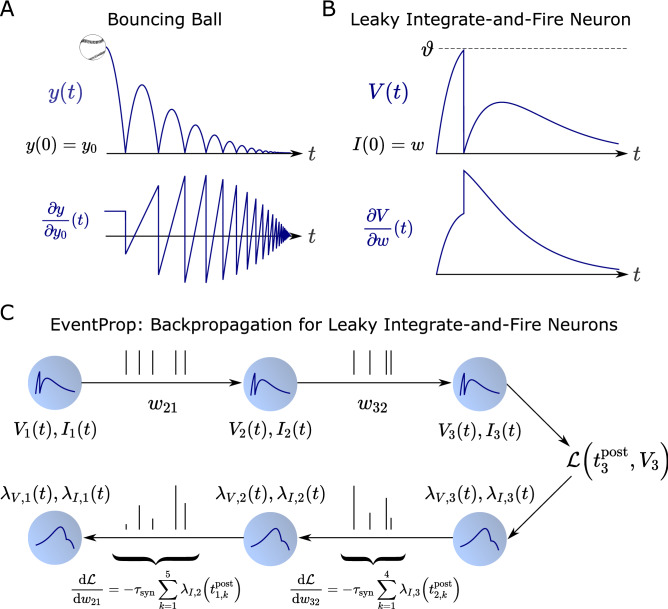
Figure 1.

We derive the precise analogue to backpropagation for spiking neural networks by applying the adjoint method together with the jump conditions for partial derivatives at state discontinuities, yielding exact gradients with respect to loss functions based on membrane potentials or spike times. (A, B) Dynamical systems with parameter-dependent discontinuous state transitions typically have discontinuous partial derivatives of state variables with respect to system parameters⁴, as is the case for the two examples shown here. Both examples model dynamics occurring on short timescales, namely inelastic reflection and the neuronal spike mechanism, using an instantaneous state transition. We denote quantities evaluated before and after a given transition by − and $+$. In A, a bouncing ball starts at height $y_0>0$ and is described by $\ddot{y}=-g$ with gravitational acceleration g. It is inelastically reflected as ${\dot{y}}^{+}=-0.8{\dot{y}}^{-}$ as soon as $y^{-}=0$ holds, causing the partial derivative with respect to $y_0$ to jump as $\frac{\partial y^{+}}{\partial y_0}=-0.8\frac{\partial y^{-}}{\partial y_0}$ (see first methods subsection). In B, a leaky integrate-and-fire neuron described by the system given in Table 1 with initial conditions $I(0)=w$, $V(0)=0$ resets its membrane potential as $V^{+}=0$ when $V^{-}=\vartheta$ holds, causing the partial derivative to jump as $\frac{\partial V^{+}}{\partial w}=\left(\frac{\vartheta }{{\tau }_{\text{mem}}{\dot{V}}^{-}},+,1\right)\frac{\partial V^{-}}{\partial w}$ (see methods for the full derivation). (C) Applying the adjoint method with partial derivative jumps to a network of leaky integrate-and-fire neurons (Table 1) yields the adjoint system (Table 2) that backpropagates errors in time. EventProp is an algorithm (Algorithm 1) returning the gradient of a loss function with respect to synaptic weights by computing this adjoint system. The forward pass computes the state variables V(t), I(t) and stores spike times $t_{}^{\text{post}}$ and each firing neuron’s synaptic current. EventProp then performs the backward pass by computing the adjoint system backwards in time using event-based error backpropagation and gradient accumulation: each time a spike was transferred across a given synaptic weight in the forward pass, EventProp backpropagates the error signal represented by the adjoint variables ${\lambda }_V(t_{}^{\text{post}})$, ${\lambda }_I(t_{}^{\text{post}})$ of the post-synaptic (target) neuron and updates the corresponding component of the gradient by accumulating ${\lambda }_I(t_{}^{\text{post}})$, finally yielding sums as given in the figure