Figure 2.
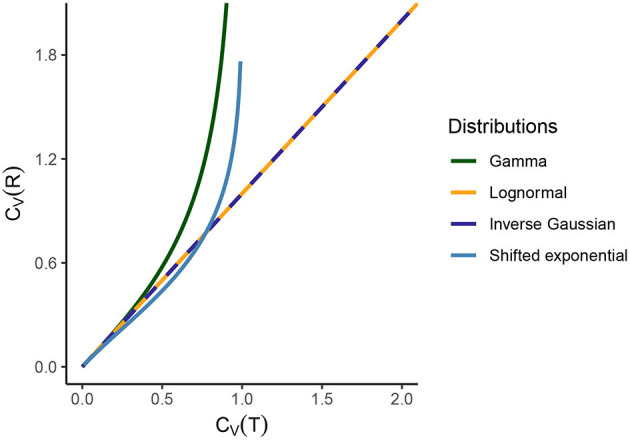
Comparison of CV(T) and CV(R) for several standard statistical ISI models. For the gamma distribution, CV(R) → ∞ as CV(T) → 1, since gamma distribution becomes exponential for CV(T) = 1. For lognormal and inverse Gaussian distribution, the relationship between the dispersion coefficients is an identity. For shifted exponential distribution, CV(T) and CV(R) depend on the mean firing rate λ and the refractory period τ. Hence, we vary the value of CV(T) and CV(R) (consequently of λ and τ) and we see that CV(R) > CV(T) until CV(T) = 0.7715 but then instantaneous rate distribution maintains a higher variability than ISIs. As CV(T) → 1, the shifted exponential becomes exactly exponential and therefore CV(R) → ∞.
