Abstract
Reactive oxygen species (ROS) play a crucial role in many physiological processes. However, ROS overproduction leads to oxidative stress, which plays a critical role in cell injury/death and the pathogenesis of many diseases. Members of NADPH oxidase (NOX) family, most of which are comprised of membrane and cytosolic components, are known to be the major nonmitochondrial sources of ROS in many cells. NOX2 is a widely-expressed and well-studied NOX family member, which is activated upon assembly of its membrane subunits gp91phox and p22phox with its cytosolic subunits p40phox, p47phox, p67phox, and Rac, facilitating ROS production. NOX2 activation is also enhanced by GTP and inhibited by GDP. However, there remains a lack of a mechanistic, quantitative, and integrated understanding of the kinetics and regulation of the assembly of these subunits and their relative contributions toward NOX2 activation and ROS production. Toward this end, we have developed a mechanistic computational model, which incorporates a generalized random rapid equilibrium binding mechanism for NOX2 assembly and activation as well as regulations by GTP (activation), GDP (inhibition), and individual subunits enhancing the binding of other subunits (mutual binding enhancement). The resulting model replicates diverse published kinetic data, including subunit concentration-dependent NOX2 activation and ROS production, under different assay conditions, with appropriate estimates of the unknown model parameters. The model provides a mechanistic, quantitative, and integrated framework for investigating the critical roles of NOX2 subunits in NOX2 assembly and activation facilitating ROS production in a variety of physiological and pathophysiological conditions. However, there is also a need for better quantitative kinetic data based on current understanding of NOX2 assembly and activation in order to test and further develop this model.
Keywords: Phagocyte oxidase, cell membrane oxidase, NOX2 assembly and activation, reactive oxygen species production, enzyme kinetics
Introduction
Reactive oxygen species (ROS), such as superoxide () and hydrogen peroxide (H2O2), are produced in cells from partial reduction of O2 through several processes; for example, mitochondrial respiration [1–3], enzymatic reactions of xanthine oxidase (XO) [4–6] and NADPH oxidase (NOX) [7–12], or interactions with xenobiotic compounds [13]. ROS plays an important role in various physiological functions, including innate immunity, regulation of redox-dependent cell signaling cascades, cell proliferation and differentiation, and production of hormones [13–19]. Oxidative stress refers to imbalance between pro- and anti-oxidant processes due to either excess ROS production or deficiency in antioxidants capacity, which leads to macromolecular (e.g. DNA, proteins, lipids) damage and cell injury/death, ultimately leading to various diseases [1–3,13,19].
Members of NOX family, most of which are comprised of membrane and cytosolic proteins, are known to be the major nonmitochondrial sources of ROS in various tissues/cells [7–12]. Different NOX complexes are formed and activated on the cell membrane in response to different stimulatory signals (e.g. growth factors, cytokines, Ca2+). ROS production, which is the primary result of the catalytic function of an assembled and activated NOX complex, varies between cell types. This property of NOX family is very different from other ROS generating systems for which ROS are byproducts of their usual physiological function (e.g. mitochondria). The physiological function of NOXs (via ROS production) includes regulation of cell signaling, gene expression, cell growth and division, and host cell defense among others [10,12,14–18,20]. NOX deficiencies/defects have been linked to immunosuppression, hypothyroidism, and chronic granulomatous disease [15,21,22]. There is also ample evidence that excess ROS generated by NOXs play a critical role in the pathogenesis of many chronic diseases, such as atherosclerosis, heart disease, lung disease, kidney disease, hypertension, diabetes, aging, neurodegeneration, and cancer [10,12,13,23–28].
Seven NOX family members (NOX1–5 and DUOX1–2) have been identified. The membrane components of each consist of at least six transmembrane α-helixes, two iron-heme groups, an FAD molecule, and an NADPH-binding domain [7–12,26]. The NOX family members differ in their membrane and cytosolic components, modes of activation, and reaction products. For example, activated NOX1–3 and NOX5 mainly produce , while activated NOX4 and DUOX1–2 mainly produce H2O2 [10–12,29]. NOXs have been found in fungi, plants, invertebrates, and in multiple tissues/organs in mammals [10–12,30]. Among these, NOX1 is highly expressed in the colon [26], NOX3 is highly expressed in the inner ear [31], and NOX4 and NOX5 are highly expressed in the kidney and blood vessels and have been implicated in the regulation of blood pressure [27,32–35].
NOX2, originally discovered in neutrophils and other phagocytes, is a widely-expressed, highly orchestrated, and well-studied NOX family member [7–12]. NOX2 plays a key role in autoimmunity and malignancy [36], as demonstrated by the reduction of lung metastases in NOX2-deficient mice [37]. Deficiency in some key components of NOX2 is also known to lead to a rare genetic disorder, namely the chronic granulomatous disease [22,38,39]. Several early studies on NOX2-activated production were carried out by Pick and colleagues in cell-free systems, stimulated through unsaturated fatty acids and sodium dodecyl sulfate (SDS) [40,41]. In addition, exogenous FAD-dependent NOX2 activation and production was shown to occur through relipidated cytochrome b558 (Cytb558) in the absence of NOX2 cytosolic components, demonstrating that membrane flavocytochrome b558 (Flavocytb558) alone is sufficient to produce as it comprises the electron transport apparatus of NOX2 [42,43]. Subsequently, the kinetic features of NOX2 assembly and activation in vitro using purified relipidated and reflavinated Cytb558 and recombinant cytosolic components activated by lithium dodecyl sulfate (LDS) were also demonstrated [44]. Though several aspects of NOX2 assembly and activation differ between cell-based and cell-free systems (e.g. distinct roles of cytosolic subunits p47phox and p67phox [44–49]; distinct mechanisms of activation (see below)), due to its enormous simplicity and ease of manipulation, the cell-free systems have been extensively used to study different aspects of NOX2 assembly and activation.
The components of NOX2 complex include two transmembrane proteins gp91phox (also known as Nox2 protein) and p22phox and four cytosolic proteins p40phox, p47phox, p67phox, and small GTPase Rac1/2 (Figure 1(A,B); phox refers to phagocyte oxidase). Activation of NOX2 requires the binding of phosphorylated/activated cytosolic subunits p47phox and p67phox or the p47phox.p67phox complex as well as Rac-GTP (active) to the membrane subunits complex gp91phox.p22phox, which constitutes Flavocytb558 (Figure 1(B)) [38,44,45,48–55]. In addition, p40phox is shown to be required for NOX2 activation in phagosomes [55–57]. The activated NOX2 complex mediates the transfer of electrons from the substrate NADPH to molecular O2 resulting in production through its catalytic action. The activated NOX2 complex is also shown to be highly specific to NADPH, responding poorly to NADH [58]. Each of the cytosolic subunits contributes towards NOX2 activation to varying extents, depending on the concentrations of these subunits and the concentrations of guanine nucleotides (GTP and GDP) [46,47,59–64]. NOX2 activation in cell-free assays was found to be enhanced by GTP and inhibited by GDP [59,60]. The regulation of NOX2 activation by GTP and GDP in cell-based assays has been attributed to the dissociation of Rac-GDP from the RhoGDI-RacGDP complex and the exchange of GTP for GDP on Rac (resulting in Rac activation) involving the complex Rho/Rac GTPase regulation cycle [14,65–70].
Figure 1.

NOX2 enzyme at resting and activated states. (A) Schematics shows NOX2 enzyme at resting state (unassembled and inactivated), where the membrane and cytosolic subunits are separated on the cell membrane and in the cytosol, respectively. Rac exists in an inactive GDP-bound form, and the p40phox, p47phox and p67phox subunits are also in inactive forms. (B) Schematics shows NOX2 enzyme complex upon assembly and activation, which facilitates electron transfer from the substrate NADPH to O2 resulting in production. The activation of NOX2 requires the binding of activated p47phox, p67phox and Rac (GTP-bound form), and optionally activated p40phox that further enhances NOX2 activity, to the complex p22phox.p67phox on the cell membrane.
During NOX2 activation, p22phox forms a mutually stabilising complex with gp91phox on the cell membrane, with its carbonyl terminus enabling the binding of phosphorylated/activated cytosolic subunit p47phox [38,52–55]. Concomitantly, the phosphorylated/activated cytosolic subunit p67phox and Rac in GTP-bound form (active) attach directly to gp91phox of Flavocytb558 [48, 49, 53, 54, 70]. The binding of p67phox in combination with Rac and other cytosolic subunits (p47phox and/or p40phox) to Flavocytb558 makes the complex to transfer electrons at a significant rate. It has also been shown that the subunit p47phox is required for the electron transfer to proceed beyond the flavin center to heme site in Flavocytb558 and then to molecular O2 for production [46,47,63]. Furthermore, p40phox has been shown to enhance the binding of p47phox to p22phox, thereby enhancing NOX2 activation and production [64]. It has also been shown that the binding of p47phox to p22phox influences the binding of p67phox to gp91phox and vice versa, based on which the so-called “mutual binding enhancement hypothesis” was proposed [61]. Some of these cell-free studies have provided us the key kinetic data required for the development of the present computational model. The data utilized in this model also include the evidence that NOX2 activity is enhanced by micromolar [GTP] and reduced by millimolar [GDP] [59,60], and the data showing that Rac in GTP-bound form (active) can translocate and bind to Flavocytb558 independent of other NOX2 cytosolic subunits [50,51], thereby enhancing the binding of p67phox [62].
Despite a considerable number of biochemical studies regarding NOX2 assembly and activation, there is a lack of a mechanistic and quantitative understanding of the kinetics and regulation of the assembly of NOX2 subunits and their relative contributions toward the oxidase activation and generation. Moreover, although experimental studies have considered the contributions of various cytosolic subunits and the effects of various regulators (e.g. GTP and GDP), NOX2 kinetics have not been considered from an integrated prospective, which enables the development of quantitative hypotheses. We therefore recently developed a thermodynamically constrained computational model [71] that provides the kinetics and regulation of the NOX2 complex-mediated electron transfer and production upon its assembly and activation. The model was developed using multiple published datasets describing NOX2 kinetics in different assay systems [58,72–77]. However, the kinetics and regulation of the different cytosolic subunit concentration-dependent NOX2 assembly and activation facilitating production were not considered in that study [71].
The objective of the present study was therefore to develop a mechanistic computational model of NOX2 assembly and activation facilitating production. The model is based on a generalized random rapid equilibrium binding mechanism for the binding of cytosolic p40phox, p47phox, p67phox, and Rac to the membrane gp91phox. p22phox complex (Flavocytb558) toward NOX2 assembly and activation. It also includes the regulation of NOX2 assembly and activation by guanine nucleotides (GTP and GDP) and individual subunits enhancing the binding of other subunits (i.e. mutual binding enhancement hypothesis). This model provides the first quantitative and integrated understanding of the kinetics and regulation of NOX2 assembly and activation facilitating production in diverse experimental preparations from different groups. In addition, it provides a mechanistic and quantitative framework for investigating the critical role of NOX2 in production, which plays a key role in the regulation of diverse cellular mechanisms in health and disease.
Materials and methods
Proposed kinetic mechanism for NOX2 assembly and activation facilitating superoxide production
Upon assembly and activation (Figure 1(B)), the NOX2 complex catalyzes the production of two molecules of by transferring two electrons from NADPH to two molecules of O2 through different redox centers of gp91phox.p22phox or Flavocytb558 (i.e. FAD and heme/Cytb558) [71]:
| (1) |
In contrast, the resting NOX2 (unassembled and inactivated; Figure 1(A)) does not enable electrons transfer from NADPH to the flavin center or beyond at a significant rate, as shown by the absence of a significant reduction of flavin or heme site of Flavocytb558 [46,47,63]. Under this scenario, the gp91phox and p22phox subunits co-stabilize one another on the cell membrane, while the cytosolic subunits p40phox, p47phox and p67phox exist in inactive (unphosphorylated) forms and Rac exists in GDP-bound (inactive) form. Upon stimulation, there is an exchange of GDP for GTP leading to Rac activation (Rac becomes GTP-bound) and its translocation to the cell membrane and its interaction with the gp91phox.p22phox complex [14,50,51,65–70]. Concomitant phosphorylation of the subunits p47phox and p67phox by protein kinases leads to their activation, allowing their translocation and interactions with the p22phox.gp91phox complex on the cell membrane [38,48,49,52–55]. This phosphorylation-translocation is one of the major events of the oxidase activation.
We assume that the binding of phosphorylated/activated cytosolic subunits p40phox, p47phox, p67phox and Rac to the membrane gp91phox.p22phox complex (Flavocytb558) occurs in a random order and rapid equilibrium manner with p40phox not contributing significantly to the assembly and activation of NOX2 in the absence of p47phox. These events are illustrated in Figure 2 with the membrane gp91phox.p22phox complex denoted as E. The K′i s (i = p47phox, p67phox, Rac) denote the apparent dissociation/binding constants for the cytosolic subunits rapid equilibrium binding reactions with the membrane subunits, as determined by the phosphorylation status of the cytosolic subunits and the levels of GTP and GDP. K′i s are the measures of the affinities of the cytosolic subunits for the membrane subunits, which depend on the particular experimental system (cell-free or cell-based) employed in a given study as well as the levels of GTP, GDP, p40phox, p47phox, p67phox, and Rac.
Figure 2.

Proposed kinetic mechanism for NOX2 assembly and activation facilitating superoxide production. Schematics shows our postulated generalized random rapid equilibrium binding mechanism for NOX2 assembly and activation, where E represents the membrane subunits complex p22phox.gp91-phox, which constitute flavocytochrome b558 (Flavocytb558) to which the cytosolic subunits p47phox, p67phox and Rac bind upon their activation. As per the proposed mechanism, E can first bind to any of the NOX2 cytosolic subunits (p47phox, p67phox, Rac) in a rapid equilibrium manner and then the rest of the subunits can bind to the complex in a similar manner to form the highly activated multi-subunit enzyme complex E.p47phox.p67phox.Rac, with K′i (i = p47phox, p67phox, Rac) representing the apparent dissociation constants for the respective subunits rapid equilibrium binding reactions with the membrane subunits. In the schematics, p47 = p47phox, p67 = p67phox, and Rac = Rac1 or Rac2.
Key experimental data characterizing the cytosolic subunit concentration-dependent NOX2 reaction flux
In order to identify the unknown model parameters characterizing the proposed kinetic mechanism, six sets of experimental data collected by four different groups are utilized. Two sets of these data are from Uhlinger et al. [60,61], who studied the effects of guanine nucleotides (GTP and GDP) and the binding of cytosolic subunits (p47phox and p67phox) to the membrane subunits complex gp91phox.p22phox (Flavocytb558) on NOX2 activation and production. Uhlinger et al. [60] used a semi-recombinant cell-free NOX2 activation system (i.e. that included isolated plasma membrane with recombinant cytosolic components) to investigate the activating role of GTP and inhibiting role of GDP on p47phox and p67phox (no p40phox and Rac) dependent NOX2 assembly, activation, and production. In another study, the same group used a similar enzyme activation system to investigate the effects of p47phox and p67phox on one another’s binding to Flavocytb558 to activate NOX2 and produce (no p40phox; 2 μM Rac; 10 μM GTP) [61]. Another set of data utilized for parameter identification is from Peveri et al. [59], who studied the enhancing effect of GTP on NOX2 activity in a similar cell-free system (no p40phox and Rac) to determine production as a function of GTP concentration. The fourth set of data utilized for parameter identification is from Nisimoto et al. [62], who used a cell-free system similar to that used by Peveri et al. [59] to investigate the effects of p67phox and Rac on one another’s binding with Flavocytb558 to activate NOX2 and produce (no p40phox and p47phox; 10 μM GTP).
Additional two sets of data utilized for parameter identification were collected by Cross et al. [63,64]. They studied the effects of the binding of cytosolic subunits p40phox, p47phox, p67phox, and Rac to the membrane subunits gp91phox and p22phox on NOX2 activity, production, and regulation of p47phox binding affinity by p40phox. Cross et al. used fully recombinant cell-free systems to determine Flavocytb558 and cytosolic subunit concentration-dependent NOX2 activation and production, and their regulations through p40phox–p47phox interactions in the presence of saturating concentrations of GTP, NADPH and O2. In one study, p47phox, p67phox and Rac concentration-dependent NOX2 activity and production were assessed by varying one subunit concentration while maintaining the other two subunits concentrations at their saturating levels and doubling the concentration of Flavocytb558 [63]. In another study, the role of p40phox in NOX2 activation was evaluated in the presence and absence of p47phox, which showed that p40phox contributes very little towards NOX2 activation in the absence of p47phox. However, p40phox did enhance the binding of p47phox to p22phox, thereby increasing NOX2 activity and production [64].
Computational model describing NOX2 reaction flux
Based on our postulated generalized random rapid equilibrium binding mechanism for NOX2 assembly and activation in Figure 2, and the detailed derivation described in Appendix A, NOX2 reaction flux at saturating concentrations of NADPH and O2 is described by Equation 2:
| (2) |
where CEtot = CFlavocytb558 denotes the total Flavocytb558 concentration; kNOX2 denotes NOX2 catalytic constant; Cp47, Cp67 and CRac denote the concentrations of p47phox, p67phox and Rac, respectively; K′p47, K′p67 and K′Rac denote the apparent binding constants for p47phox, p67phox and Rac, respectively. The superscript “phox” is eliminated from the equation for simplicity. It should be noted here that at limiting concentrations of the substrates NADPH and O2, the NOX2 catalytic constant kNOX2 is a function of [NADPH] and [O2], as shown in our recent publication [71]. More details on the derivation of NOX2 reaction flux can be found in Appendix A. We note here that, in our model formulation (Figure 2), p40phox is not essential for NOX2 assembly and activation, and hence it does not appear in Equation (2), which is valid for the plasma membrane.
As noted in the description of the experimental data from Uhlinger et al. [61], the binding of p47phox to Flavocytb558 influences the binding of p67phox to Flavocytb558 and vice-versa, indicating a regulatory role of p47phox on p67phox binding and vice versa (mutual binding enhancement). In addition, based on the data from Nisimoto et al. [62], the binding of p67phox to Flavocytb558 influences the binding of Rac to Flavocytb558 and vice-versa, suggesting a regulatory role of p67phox on Rac binding and vice versa (mutual binding enhancement). Based on our generalized model formulation, the same mutual binding enhancement also exists between p47phox and Rac, indicating a regulatory role of p47phox on Rac binding and vice versa. Based on the data of Cross et al. [64], p40phox enhances the binding of p47phox increasing NOX2 activity and production, whose effect is accounted for in our model via K′p47 in Equation 3(a) below. Moreover, NOX2 activity is enhanced by micromolar of GTP and attenuated by millimolar of GDP [59,60]. For the sake of generality in our model formulation, we also postulate that Rac binding to Flavocytb558 enhances the binding of p47phox and p67phox to Flavocytb558. The apparent binding constants K′p47, K′p67 and K′Rac can then be phenomenologically expressed based on the standard Michaelis–Menten kinetic formulation for activations and inhibitions as follows:
| (3a) |
| (3b) |
| (3c) |
where CGTP and CGDP denote the concentrations of GTP and GDP, respectively; KGTP and KGDP denote the regulatory constants for GTP and GDP to enhance and inhibit NOX2 activity, respectively; nT and nD are the corresponding Hill coefficients; K″p47p67 and K″p47Rac are the regulatory constants for p47phox to enhance the binding of p67phox and Rac, respectively; K″p67p47 and K″p67Rac are the regulatory constants for p67phox to enhance the binding of p47phox and Rac, respectively; K″Racp47 and K″Racp67 are the regulatory constants for Rac to enhance the binding of p47phox and p67phox, respectively; and K″p40 is the regulatory constant for p40phox to enhance the binding of p47phox. The regulatory effect of p40phox can be simply eliminated by substituting Cp40 = 0 or by significantly increasing the value of K″p40 in Equation 3(a).
A Hill coefficient (nH) characterizes the cooperative binding of a ligand to a macromolecule. Although cooperativity often enhances the binding (positive cooperativity; nH > 1), it can also decrease the binding (negative cooperativity; nH < 1) or show no effect (nH = 1). The Hill coefficients nT and nD are incorporated into our model for simulating the guanine nucleotides-dependent regulations (i.e. enhancement by GTP and inhibition by GDP) of NOX2 activity observed in the studies of Uhlinger et al. [60] and Peveri et al. [59] (no Rac; no GTP-GDP exchange on Rac).
Model simplification
The model can be further simplified in terms of the number of unknown parameters by assuming the same extent regulatory effects of the individual cytosolic subunits with the other cytosolic subunits by applying the following constraints:
| (4a) |
| (4b) |
| (4c) |
Here, we have assumed that p47phox binding to the membrane subunits enhances p67phox binding to the same extent as Rac binding (Equation (4a)); p67phox binding to the membrane subunits enhances p47phox binding to the same extent as Rac binding (Equation (4b)); and Rac binding to the membrane subunits enhances p47phox binding to the same extent as p67phox binding (Equation (4c)). These constraints reduce the number of unknown parameters by three, but a key question is whether such parameter reduction affords a good fit of the model solution to the available data. To test this, we have characterised three nested models (Models 1, 2 and 3; see Appendix B), based on the number of unknown parameters. Model 3 corresponds to Equations (2) and (3) without any parameter constraint; Model 2 corresponds to Equations (2) and (3)) with the parameter constraint of Equation (4); and Model 3 corresponds to Equations (2) and (3) with the parameter constraint of Equation (4) and with K″p47 = 0, K″p67 = 0, and K″Rac = 0.
Numerical estimation of NOX2 model parameters
Each of the kinetic models developed for NOX2 assembly and activation facilitating production contains several unknown parameters. The number of unknown parameters depends on the complexity of a particular model. As described above, Model 3 has 12 unknown parameters, Model 2 has 9 unknown parameters, and Model 1 has 6 unknown parameters. The parameter estimation for these three models entailed a combined use of all the available experimental data related to NOX2 subunits assembly, activation, and production [59–64] and minimizing the sum of squared differences error function (Equation (5)) for fitting the model solutions to these experimental data:
| (5) |
where Nexp is the number of experiments; Ndata,k is the number of data points in the kth experiment; are the experimental data; and are the corresponding model solutions that depend on the values of the model parameters ϕ. The accuracy in the estimated model parameters values and the robustness of the model fits to the experimental data are assessed based on the value of the sum of squared differences error function E(ϕ) and statistical modelling criteria. Our approach for parameter estimation and testing the robostness of the model fits are detailed in Appendix B.
Results
The parameterization results of the three competing models of NOX2 assembly and activation showed that Model 3 with 12 unknown parameters resulted in the least sum of squared differences of 3.01 and the best fit to the available data. Therefore, Model 3 was considered as the best model of NOX2 assembly and activation, and the estimated parameter values and simulation results for Model 3 are presented in this section. In parametrizing the model, a hybrid Monte-Carlo and Fmincon approach in MATLAB was used as detailed in Appendix B. This resulted in parameter values shown in Table 1 for which Model 3 solution best fits the kinetic data of Cross et al. [63,64] as shown in Figure 3, and parameter values in Table 2 for which Model 3 solution best fits the kinetic data of Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62] as shown in Figures 4 and 5. Model 3 was also used to predict other kinetic data shown in Figures 6 and 7 that were not used for model parameterization in addition to Figure 8 to corroborate the model and estimated parameter values. In what follows, all the simulation results were generated using Model 3 using the parameters values in Tables 1 and 2.
Table 1.
Estimated parameter values for the model (Model 3 = Model 2 = Model 1) of NOX2 assembly and activation, fitted jointly to the experimental data of Cross et al. [63,64].
| Parameter | Definition/Comments | Value | Units |
|---|---|---|---|
| CEtot | Total NOX2 enzyme concentration (known from the experimental conditions) | Vary depending on the experiment/assay | μM |
| kNOX2 | NOX2 catalytic constant (Cross [64]) | 826.7 | 1/sec |
| kNOX2 | NOX2 catalytic constant (Cross et al. [63]) | 204.5 | 1/sec |
| K′p47 = Kp47 | p47phox binding constant for the membrane subunits | 0.029 | μM |
| K′p67 = Kp67 | p67phox binding constant for the membrane subunits | 0.00038 | μM |
| K′Rac = KRac | Rac binding constant for the membrane subunits | 0.00063 | μM |
| p40phox regulatory constant for the p47 binding enhancement | 0.005 | μM |
Figure 3.
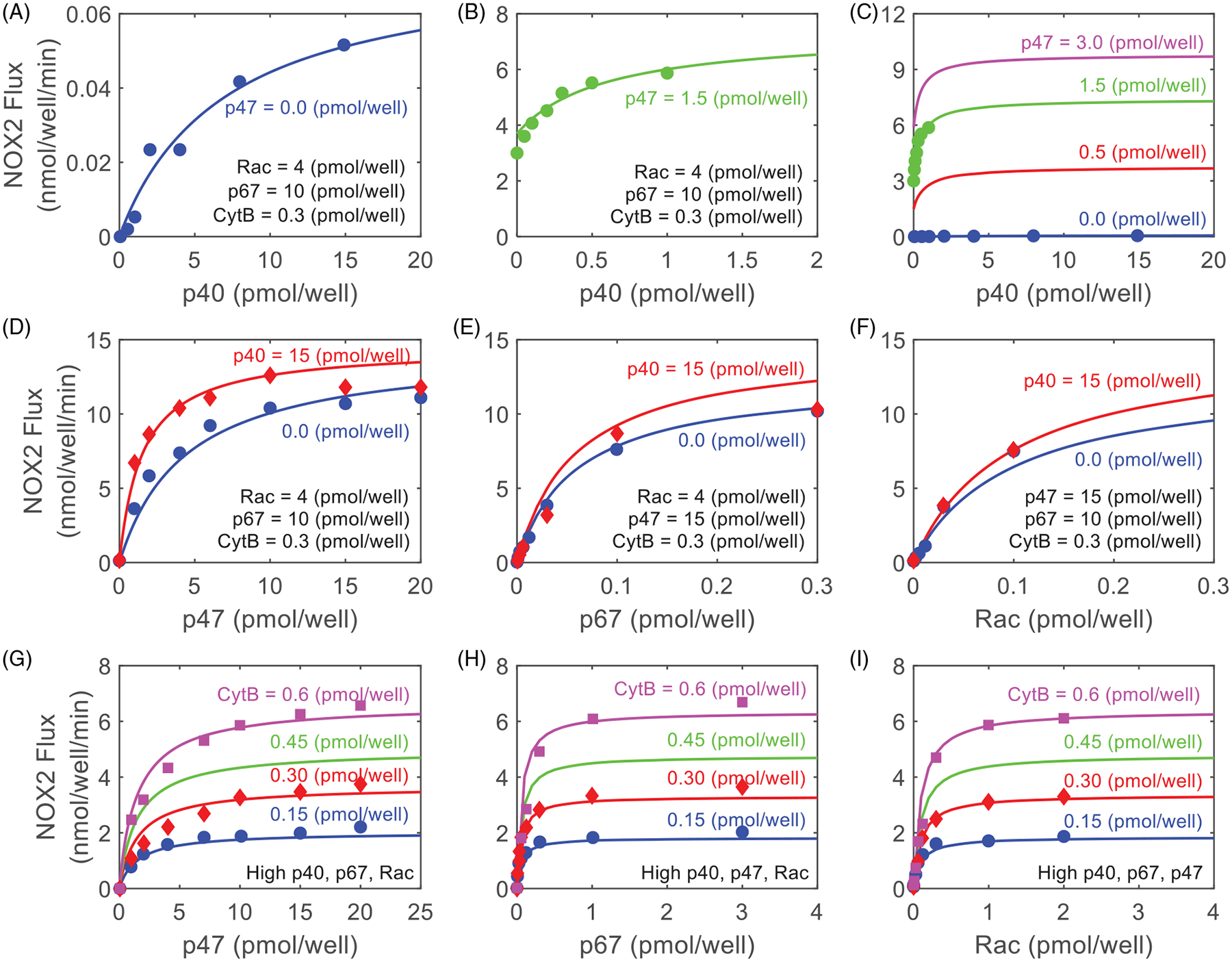
Model fittings to the experimental data of Cross et al. [63,64] on the cytosolic subunit concentration-dependent NOX2 assembly, activation, superoxide production, and regulation by p40phox and p47phox interactions in cell-free systems. (A–C) Model simulations (lines) are compared to the experimental data (points) of Cross [64] on the effects of p47phox on the saturation kinetics and regulation of NOX2 reaction flux (rate of production) with respect to varying concentrations of p40phox at different concentrations of p47phox with fixed Rac concentration of 4 pmol/well, p67phox concentration of 10 pmol/well, and Flavocytb558 concentration of 0.3 pmol/well. Panels A and B are zoomed-in forms of Panel C for the concentration of p47phox at 0.0 pmol/well and 1.5 pmol/well, respectively. Where p47phox is zero, it is substituted with p40phox in Equation (2). (D–F) Model simulations (lines) are compared to the experimental data (points) of Cross [64] on the effects of p40phox on the saturation kinetics and regulation of NOX2 reaction flux (rate of production) with respect to varying concentrations of the subunits p47phox, p67phox and Rac, respectively, at two different concentrations of p40phox (0 and 15 pmol/well) with fixed Flavocytb558 concentration of 0.3 pmol/well. In Panel D, concentrations of Rac and p67phox are fixed at 4 pmol/well and 10 pmol/well, respectively. In Panel E, concentrations of Rac and p47phox are fixed at 4 pmol/well and 15 pmol/well, respectively. In Panel F, concentrations of p47phox and p67phox are fixed at 15 pmol/well and 10 pmol/well, respectively. (G-I) Model simulations (lines) are compared to the experimental data (points) of Cross et al. [63] on the effects of Flavocytb558 on the saturation kinetics and regulation of NOX2 reaction flux (rate of production) with respect to varying concentrations of the subunits p47phox, p67phox and Rac, respectively, at different concentrations of Flavocytb558. In Panel G, p67phox, p40phox and Rac are present at high concentrations. In Panel H, p47phox, p40phox and Rac are present at high concentrations. In Panel I, p67phox, p47phox and p40phox are present at high concentrations. Model-simulated lines for NOX2 flux for Flavocytb558 concentration of 0.6 pmol/well and 0.15 pmol/well are within ±10% of the reported values. Cross et al. [63,64] studied the kinetics and regulation of NOX2 assembly, activation, and production in a cell-free system, that is, in an in vitro 150 μL well containing different concentrations of Flavocytb558 and cytosolic subunits, as indicated in the plots. Model simulations were carried out using the estimated parameter values in Table 1.
Table 2.
Estimated and fixed parameter values for Model 2 and Model 3 for NOX2 assembly and activation, fitted jointly to the experimental data of Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62].
| Parameter | Definition/Comments | Model 2 Values | Model 3 Values | Units |
|---|---|---|---|---|
| CEtot | Total NOX2 enzyme concentration (known from the experimental conditions) | Vary depending on the experiment/assay | Vary depending on the experiment/assay | μM |
| kNOX2 | NOX2 catalytic constant | 155 | 160 | 1/sec |
| Kp47 | p47phox binding constant for the membrane subunits | 0.21 | 0.24 | μM |
| Kp67 | p67phox binding constant for the membrane subunits | 0.05 (fixed) | 0.06 | μM |
| KRac | Rac binding constant for the membrane subunits | 0.20 | 0.22 | μM |
| K″p67p47 | p67phox regulatory constant for enhancing the p47phox binding affinity | 0.28 (K″ p67) | 0.30 | μM |
| K″Racp47 | Rac regulatory constant for enhancing the p47phox binding affinity | 0.11 (K″ Rac) | 0.05 | μM |
| K″p47p67 | p47phox regulatory constant for enhancing the p67phox binding affinity | 0.03 (K″ p47) | 0.11 | μM |
| K″Racp67 | Rac regulatory constant for enhancing the p67phox binding affinity | 0.11 (K″ Rac) | 0.33 | μM |
| K″p47Rac | p47phox regulatory constant for enhancing the Rac binding affinity | 0.03 (K″ p47) | 0.009 | μM |
| K″p67Rac | p67phox regulatory constant for enhancing the Rac binding affinity | 0.28 (K″ p67) | 0.003 | μM |
| KGTP | GTP regulatory constant for enhancing the p47phox, p67phox and Rac binding affinities | 0.41 | 0.36 | μM |
| KGDP | GDP regulatory constant for inhibiting the p47phox, p67phox and Rac binding affinities | 4387 | 5561 | μM |
| Racb | Basal concentration of Rac (Uhlinger et al. [60]) | 0.02 (fixed) | 0.02 (fixed) | μM |
| GTPb | Basal concentration of GTP (Uhlinger et al. [60]) | 0.5 (fixed) | 0.5 (fixed) | μM |
| p47b | Basal concentration of p47phox (Nisimoto et al. [62]) | 0.01 (fixed) | 0.01 (fixed) | μM |
| nT | Hill coefficient for the p47phox, p67phox and Rac regulation by GTP | 2.0 (fixed) | 2.0 (fixed) | Unitless |
| nD | Hill coefficient for the p47phox, p67phox and Rac regulation by GDP | 0.5 (fixed) | 0.5 (fixed) | Unitless |
| SSD | Sum of squared differences (least squared error) | 5.85 | 3.01 | Unitless |
| AIC | Akaike’s information criterion | −581 | −692 | Unitless |
The table also includes the computed values of SSD and AIC based on the estimated and fixed parameter values.
Figure 4.

Model fittings to the experimental data of Uhlinger et al. [60] and Peveri et al. [59] on the cytosolic subunit concentration-dependent NOX2 assembly, activation, ROS production, and their regulations by guanine nucleotides in cell-free systems. (A, B) Model simulations (lines) are compared to the experimental data (points) of Uhlinger et al. [60] on the regulatory effects of GTP and GDP on the saturation kinetics of NOX2 reaction flux (rate of production) with respect to varying concentration of the subunit p47phox with fixed p67phox concentration of 1.3 μM (A) and varying concentration of the subunit p67phox with fixed p47phox concentration of 1.3 μM (B), under the presence of a nominal Rac concentration of 0.02 μM. Varying concentrations of GTP and GDP or no nucleotide present were included, as indicated in the plots. Model-simulated lines for NOX2 flux are within ±10% of the reported values. (C, D) Model simulations demonstrating the roles of GDP as an inhibitory factor and GTP as a stimulatory factor for NOX2 assembly, activation, and production are compared to available experimental data [59,60], with the subunits p47phox, p67phox and Rac concentrations are as indicated in the plots. In all experiments of Uhlinger et al. [60], 50 μl of reaction mixtures (pH = 7.4) contained 10 μg of plasma membrane (PM), or equivalently 8.6 pmol of Flavocytb558, providing an appropriate concentration of total NOX2 complex for model simulations. For the experimental data of Peveri et al. [59], NOX2 flux was multiplied by a factor of 5.7 to be in the same range of NOX2 flux as in the experimental data of Uhlinger et al. [60] for a comparative data analysis. In addition, the substrates NADPH and O2 concentrations were very high (250 μM, saturated) in all experiments. Model simulations were carried out using the estimated parameter values in Table 2.
Figure 5.

Model fittings to the experimental data of Uhlinger et al. [61] and Nisimoto et al. [62] on the mutual enhancements of cytosolic subunits binding to the membrane subunits in cell-free systems. (A, B) Model simulations are compared to the experimental data of Uhlinger et al. [61] on the regulatory effects of the subunits p47phox and p67phox on each other’s binding enhancement to the membrane subunits which in turn increases NOX2 activity (mutual binding enhancement). Specifically, the plots show the rates of production via the assembled and activated NOX2 complex as functions of varying concentrations of the cytosolic subunits p47phox and p67phox, with Rac concentration fixed at 2.02 μM in the presence of 10.5 μM GTP (absence of GDPβS). (C, D) Model simulations are compared to the experimental data of Nisimoto et al. [62] on the regulatory effects of the subunits Rac and p67phox on each other’s binding enhancement to the membrane subunits which in turn increases NOX2 activity (mutual binding enhancement). Specifically, the plots show the rates of production via the assembled and activated NOX2 complex as functions of varying concentrations of the cytosolic subunits p67phox and Rac, with p47phox concentration fixed at 0.01 μM in the presence of 10.5 μM GTPγS (absence of GDPβS). Model-simulated lines for NOX2 flux as a function of Rac and p67phox are within ±10% of the reported values. In all experiments of Uhlinger et al. [61], 50 μl of reaction mixtures (pH = 7.4) contained 10 μg of plasma membrane (PM), or equivalently 8.6 pmol of Flavocytb558, providing an appropriate concentration of total NOX2 complex for model simulations. All experiments of Nisimoto et al. [62] were performed at pH of 7.4 and 10 nM Cytb558. In addition, the substrates NADPH and O2 concentrations were very high (250 μM, saturated) in both Uhlinger at al. and Nisimoto et al. experiments. Model simulations are carried out using the estimated parameter values in Table 2.
Figure 6.

Model predictions on the effects of varying concentrations of p47phox on the kinetic parameters of NOX2 model for different concentrations of GTP, GDP, and Rac. Plots show model predictions on the effects of varying concentrations of the subunits p47phox on the apparent Km and Vmax of p67phox for (A, B) different concentrations of GTP with fixed GDP and Rac at 0 mM and 2 μM, respectively, (C, D) different concentrations of GDP with fixed GTP and Rac at 10 μM and 2 μM, respectively, and (E, F) different concentrations of Rac with fixed GTP and GDP at 10 μM and 0 mM, respectively. Plots also show the experimental data that were available from the Uhlinger et al. study [61] for GTP = 10 μM, GDP = 0 mM, and Rac = 2 μM. Experimental conditions used for model simulations are exactly the same as that described in Figures 5. Model predictions were carried out using the estimated parameter values in Table 2.
Figure 7.

Model predictions on the effects of varying concentrations of p67phox on the kinetic parameters of NOX2 model for different concentrations of GTP, GDP, and Rac. Plots show model predictions on the effects of varying concentrations of the subunits p67phox on the apparent Km and Vmax of p47phox for (A, B) different concentrations of GTP with fixed GDP and Rac at 0 mM and 2 μM, respectively, (C, D) different concentrations of GDP with fixed GTP and Rac at 10 μM and 2 μM, respectively, (E, F) different concentrations of Rac with fixed GTP and GDP at 10 μM and 0 mM, respectively. Plots also show the experimental data that were available from the Uhlinger et al. study [61] for GTP = 10 μM, GDP = 0 mM, and Rac 2 μM. Experimental conditions used for model simulations are exactly the same as that described in Figure 5. Model predictions were carried out using the estimated parameter values in Table 2.
Figure 8.

Model predictions on the effects of varying concentrations of p67phox on the kinetic parameters of NOX2 model for different concentrations of GTP, GDP, and p47phox. Plots show model predictions on the effects of varying concentrations of the subunits p67phox on the apparent Km and Vmax of Rac for (A, B) different concentrations of GTP with fixed GDP and p47phox fixed at 0 mM and 16 μM, respectively, (C, D) different concentrations of GDP with fixed GTP and p47phox at 10 μM and 16 μM, respectively, and (E, F) different concentrations of p47phox with fixed GTP and GDP at 10 μM and 0 mM, respectively. Experimental conditions used for model simulations are exactly the same as that described in Figure 5. Model predictions were carried out using the estimated parameter values in Table 2.
Cytosolic subunit concentration-dependent effects on NOX2 activity and the regulatory effect of p40phox on p47phox binding based on the kinetic data of Cross et al. [63,64]
As shown in Figure 3, using the estimated model parameter values in Table 1 (Model 3 = Model 2 = Model 1), we were able to simulate very well the concentration-dependent effects of Flavocytb558, p40phox, p47phox, p67phox and Rac on NOX2 activity and the regulatory effects of p40phox on p47phox binding to Flavocytb558 in activating NOX2 enzyme in cell-free systems.
Simulations of the effect of p40phox on NOX2 activity for varying concentrations of p47phox and high (saturating) concentrations of p67phox and Rac are shown in Figure 3(A–C). The effect of p47phox at high concentrations of p67phox and Rac, the effect of p67phox at high concentrations of p47phox and Rac, and the effect of Rac at high concentrations of p47phox and p67phox in the absence and presence of high concentrations of p40phox are simulated in Figure 3(D–F). In these simulations, Flavocytb558 concentration was fixed at 0.3 pmol/well, as per the experimental protocol. Cross et al. [64] used a cell-free system to demonstrate the role of p40phox on NOX2 activity and found NOX2 activity to be very weak in the absence of p47phox. Addition of p47phox increases NOX2 activity by several hundred-fold and this enhancement could not be explained by just the additive effects of p40phox and p47phox. From this analysis, it was concluded that p40phox functions by mainly increasing the binding affinity of p47phox for Flavocytb558, thereby enhancing NOX2 activity.
Our model simulated very well the concentration-dependent effect of p40phox on NOX2 activity with very low enzyme activity in the presence of only p40phox (Figure 3(A)) and high enzyme activity in the presence of both p40phox and p47phox (Figure 3(B,C)). Model simulations also showed that p40phox does not act additively with p47phox, p67phox and Rac to enhance NOX2 activity, as depicted in Figure 3(D–F), and that the enhanced effect is achieved primarily by increasing the binding affinity of p47phox for Flavocytb558 by p40phox (Equation 3(a)). In addition, the effect of varying the concentration of Flavocytb558 on NOX2 activity [63] was simulated very well as shown in Figure 3(G–I). Flavocytb558 increased NOX2 activity in a linear concentration-dependent fashion, as observed experimentally, when the assay medium contained various concentrations of the subunits p47phox, p67phox and Rac at any level of p40phox. The model also fits quite well the Cross et al. [63] experimental data (Figure 3(G–I)), for which the concentrations of p47phox, p67phox and Rac were varied one at a time over a range of Flavocytb558 concentrations, while keeping the concentrations of other subunits fixed at maximal levels.
Regulatory effects of guanine nucleotides on NOX2 assembly, activation, and superoxide generation based on the kinetic data of Uhlinger et al. [60] and Peveri et al. [59]
As demonstrated in Figure 4, using the estimated model parameter values in Table 2 (Model 3), we were able to simulate very well the regulatory effects of GTP and GDP on NOX2 assembly, activation, and production based on the experimental data of Uhlinger et al. [60] and Peveri et al. [59].
Uhlinger et al. [60] studied the regulatory roles of guanine nucleotides (GTP and GDP) on the cytosolic subunits (p47phox and p67phox) concentration-dependent NOX2 assembly, activation, and generation with a negligible Rac level (estimated to be ~0.02 μM) and saturated NADPH and O2 levels in reconstituted cell-free systems (isolated membrane preparation). They demonstrated that 10 μM GTP maximally activated generation, while 10 mM GDP significantly inhibited generation, with appreciable baseline activity without any added GTP and GDP (due to partial activation of NOX2 enzyme by endogenously present GTP; basal activity). These kinetic data were used to model the cytosolic subunit concentration-dependent NOX2 assembly, activation, generation, and regulation by guanine nucleotides. As illustrated in Figures 4(A,B), the model nicely simulated the guanine nucleotide regulation of NOX2 activity with varying levels of p47phox and p67phox, as observed experimentally [60]. The effects of varying the levels of GTP and GDP with fixed levels of p47phox and p67phox (1.3 μM each) were then simulated at high NADPH and O2 levels and a baseline Rac level of ~0.02 μM to determine the opposing effects of guanine nucleotides on NOX2 activity. The stimulatory effect of GTP and the reciprocal inhibitory effect of GDP are illustrated in Figures 4(C,D), and are compared to the available experimental data on the inhibitory effect of GDP in the presence of 10 μM GTP [60] and the stimulatory effect of GTP in the absence of GDP [59] (dark blue lines in Figure 4(C,D)). The model predicted the GTP and GDP-induced alterations in the binding constants for the subunits p47phox and p67phox. Importantly, these model analyses suggest that the oxidase-associated GTP and GDP levels are likely to participate in NOX2 complex formation.
Regulatory effects of mutual binding enhancements between cytosolic subunits on NOX2 assembly, activation, and superoxide generation based on the kinetic data of Uhlinger et al. [61] and Nisimoto et al. [62]
As demonstrated in Figure 5, using the estimated model parameter values from Table 2 (Model 3), we were able to simulate very well the regulatory controls of NOX2 assembly, activation, and production via mutual binding enhancements between the cytosolic subunits p47phox, p67phox and Rac based on the experimental data of Uhlinger et al. [61] and Nisimoto et al. [62]. Figure 5(A,B) is based on the study by Uhlinger et al. [61] in which a reconstituted cell-free system was used to determine the influence of NOX2 subunits p47phox and p67phox upon each other’s binding to Flavocytb558 for the oxidase activity, carried out in the presence of exogenously added 2 μM Rac and 10 μM GTP. Similarly, Figure 5(C,D) is based on the study by Nisimoto et al. [62] in which a similar cell-free system was utilized to determine the influence of NOX2 subunits p67phox and Rac upon each other’s binding to Flavocytb558 for the oxidase activity, carried out in the presence of negligible p47phox (estimated to be ~0.01 μM) and 10 μM added GTP. Mutually enhanced binding of cytosolic subunits to Flavocytb558 required modification of our model by addition of regulatory mechanisms describing the kinetics of p47phox binding enhanced by p67phox and Rac via Equation 3(a), the kinetics of p67phox binding enhanced by p47phox and Rac via Equation 3(b), and the kinetics of Rac binding enhanced by p47phox and p67phox via Equation 3(c). This modified model suggests interdependent changes in the values of the apparent Km and Vmax values of NOX2 with respect to the cytosolic subunits.
As seen in Figure 5(A,B), the apparent Km and Vmax values for the subunit p47phox are modified at variable concentrations of the subunit p67phox and vice versa. In this case, the subunit Rac and GTP levels were held constant at 2.02 μM and 10.5 μM, in the presence of estimated basal concentration of 0.02 μM and 0.5 μM, respectively. Also, as seen in Figure 5(C,D), the apparent Km and Vmax values for the subunit Rac are modified at variable concentrations of the subunit p67phox and vice-versa. In this case, the subunit p47phox and GTP levels were held constant at 0.01 μM and 10.5 μM, with an estimated basal concentration of 0.01 μM and 0.5 μM, respectively. Experimentally [61,62], the rate of generation was measured at saturated NADPH and O2 levels to ascertain its dependency on the varying concentrations of the subunit p47phox at various fixed concentrations of the subunit p67phox and vice-versa for Figure 5(A,B), and on the varying concentrations of the subunit Rac at various fixed concentrations of the subunit p67phox and vice versa for Figure 5(C,D). The model simulations found that as the concentration of either of the subunits decreases, the binding of the other subunits to Flavocytb558 becomes weaker such that at lower concentrations of these subunits, NOX2 reaction flux ( production) decreases significantly.
Importantly, the model simulations of Figure 5 informed us about the mutual binding enhancements of cytosolic subunits on each other’s bindings to Flavocytb558, as evidenced by the studies of Uhlinger et al. [61] and Nisimoto et al. [62]. Based on Uhlinger et al. [60] data compared to Uhlinger et al. [61] data, the presence of the subunit Rac in the reaction mixture (2 μM added) resulted in significantly higher Vmax values (20-fold increase) showing a key regulatory role of Rac in enhancing the binding of cytosolic subunits p47phox and p67phox to Flavocytb558 as well as in significantly higher active NOX2 complex formation. In addition, based on Equation (2), our model indicates that a basal concentration of the cytosolic subunits p47phox, p67phox and Rac are required for NOX2 assembly and activation. Thus, the proposed model provides a unified theory/hypothesis that quantitatively explains these diverse experimental datasets. We have also introduced Hill coefficients to model the cooperative regulation of NOX2 cytosolic subunits binding to Flavocytb558 by guanine nucleotides, i.e. GTP and GDP (see Equations (3a–c)).
Model corroboration showing the regulations of apparent NOX2 kinetic parameters by guanine nucleotides and cytosolic subunits
The regulatory effects of guanine nucleotides (GTP and GDP) and cytosolic subunits (p47phox, p67phox, and Rac) on the binding of p47phox, p67phox, and Rac to Flavocytb558 characterizing NOX2 assembly and activation were further analyzed by our model. We computed the apparent Km and Vmax values for p67phox as a function of p47phox for different concentrations of GTP, GDP, and Rac; the apparent Km and Vmax values for p47phox as a function of p67phox for different concentrations of GTP, GDP and Rac; and the apparent Km and Vmax values for Rac as a function of p67phox for different concentrations of GTP, GDP and p47phox. These calculations were made to study the regulatory effects of varying concentrations of GTP, GDP, and cytosolic subunits at saturated concentrations of NADPH and O2 (experimental conditions exactly the same as that for Figures 4 and 5) on the apparent kinetic parameters governing the binding of cytosolic subunits to Flavocytb558. These model simulation results are shown in Figures 6–8.
The apparent NOX2 kinetic parameters are calculated numerically by equating Equation (2) for JNOX2 with K′i s defined by Equations (3a–c) with an equation of the form JNOX2 = Vmax,SCS/(Km,S+CS), where S stands for the subunits p47phox, p67phox or Rac, and CS denotes the concentration of S. This way, the apparent Km,S and Vmax,S are functions of the other variables. For example, if S = p47phox, the Km,S and Vmax,S are functions of p67phox, GTP, GDP, and Rac at saturated levels of NADPH and O2. In this case, the Vmax,S can be easily computed numerically by evaluating Equation (2) at very high CS, and the Km,S can be easily computed numerically by solving the value of CS at which the value of JNOX2 is equal to Vmax,S/2 in Equation (2). We emphasize here that, for these computations, NOX2 model structure includes all the modular components, namely the subunits assembly, guanine nucleotides regulation of the assembly, mutual binding enhancement, and production.
The results of these model predictions reveal that the apparent Km of p67phox (or p47phox or Rac) was decreased, while the apparent Vmax with respect to p67phox (or p47phox or Rac) was increased with increasing concentrations of the other subunit p47phox (or p67phox or Rac). The same was the case with increasing concentrations of GTP and decreasing concentrations of GDP. However, it is worth mentioning here that the apparent Km of p47phox did not decrease appreciably with increasing concentrations of Rac and apparent Km of Rac did not decrease appreciably with increasing concentrations of p47phox and p67phox (Figures 7(E) and 8(E)). Decreased Km,S and increased Vmax,S indicate increased binding affinity of the cytosolic subunits p47phox, p67phox, and Rac for the membrane Flavocytb558 and increased overall NOX2 activity, respectively. Therefore, p47phox appears to increase the binding affinity of p67phox for Flavocytb558 and vice versa, albeit differentially, which is consistent with the mutual binding enhancement hypothesis, originally proposed by Uhlinger et al. [61]. Our model also predicts that there is no mutual binding enhancement between p47phox and Rac, and only negligible enhancement in the binding of Rac by p67phox (see Table 2).
An important observation from the simulations in Figures 6–8 is that Km,p67 is an order of magnitude higher than Km,p47 and Km,Rac, while Vmax,p67, Vmax,p47, and Vmax,Rac are of the same order of magnitude. This indicates that p47phox enhances the binding affinity of p67phox (reduces Km,p67) 10 times more than p67phox enhances the binding affinity of p47phox and Rac (reduces Km,p47 and Km,Rac) for Flavocytb558. Furthermore, our model predictions show that GTP increases the binding affinities of p47phox, p67phox, and Rac for Flavocytb558, while GDP decreases the binding affinities of these subunits for Flavocytb558. Interestingly, our model predictions also show that there is no enhancement in the binding affinity of Rac for Flavocytb558 by p47phox and p67phox (K″p67Rac = 0.009 and K″p47Rac = 0.003; Table 2), and there is negligible enhancement in the binding affinity of p47phox for Flavocytb558 by Rac (K″Racp47 = 0.05; Table 2). The assembly and activation of NOX2 is seen to be maximal at 10 μM GTP, 0 mM GDP, and 2 μM Rac at which the apparent Km,S is minimal and the apparent Vmax,S is maximal. The model predictions in Figures 6 and 7 match well with the measured data from the experiments by Uhlinger et al. [61]. It is important to recognize that since these experimental data were not used for model parameterization, the ability of the model to predict these data provides additional support for its accuracy and utility. Also, the model predictions in Figure 8 provide a good insight into the behavior of the apparent Km and Vmax of Rac with respect to varying concentrations of p67phox for various concentrations of GTP, GDP, and p47phox.
Discussion
The goal of the present study was to develop a simple, yet adequately detailed, computational model of NOX2 assembly and activation on the cell membrane that can provide a mechanistic and quantitative understanding of the kinetics and regulation of the assembly of NOX2 subunits and their relative contributions to NOX2 activation and production. In view of the enormous complexity of the biological process of NOX2 assembly and activation, several assumptions were required to simplify the process in developing this model. The major assumption was that the assembly and activation of NOX2 occurs through random rapid equilibrium binding of its cytosolic subunits (p40phox, p47phox, p67phox, and Rac) with its membrane subunits (gp91phox and p22phox). This is further activated by GTP and inhibited by GDP and further regulated by the mutual binding enhancement mechanism, consistent with the existing literature [59–62]. The complexity of the model and the hypotheses was systematically incorporated through a modular model building and hypothesis testing approach. The model was rigorously parameterized and challenged using diverse experimental data obtained under different assay conditions [59–64], which then provided reliable and predictive representations of NOX2 assembly and activation. The ability of the model to simulate quite well a diverse spectrum of experimental data from various laboratories suggest that the underlying assumptions are reasonable. It should be emphasized that a model cannot describe experimental data from diverse sources under different assay conditions with suitable model parameter values unless appropriate kinetic mechanisms are incorporated no matter how many unknown parameters it contains, as rigorously tested in Appendix B. The model as developed represents a first step toward a quantitative and integrated understanding of several aspects of NOX2 assembly and activation, specifically how different cytosolic components (p40phox, p47phox, p67phox, and Rac) and guanine nucleotides (GTP and GDP) regulate the overall process. Consistent with the process of model building, more details of the protein–protein interactions, phosphorylation and dephosphorylation, alternative NOX2 assembly and activation mechanisms, and the regulation of the assembly and activation process by the Rho/Rac GTPase regulation cycle can be integrated into future iterations of this model as appropriate quantitative data becomes available.
The kinetic data used to develop and parameterize the model was obtained from studies by different groups in which the experiments were carried out under different assay conditions [59–64]. For example, Uhlinger et al. [60] did not initially include Rac in their studies, but rather they studied the activating effects of GTP and inhibitory effects of GDP on the overall NOX2 activity production), while varying the levels of the cytosolic subunits p47phox and p67phox. However, in a subsequent study [61], they added Rac (2 μM) to the reaction mixture with saturating level of GTP (10 μM), and thereby, they observed the mutual binding enhancements of p47phox and p67phox for Flavocytb558. Importantly, there was a 20-fold increase in the overall NOX2 activity with the addition of 2 μM Rac as a consequence of enhanced NOX2 complex formation on the cell membrane. These data were nicely recapitulated with our computational model as well as the GTP- and GDP-dependent kinetic data from Uhlinger et al. [60] and the GTP-dependent kinetic data from Peveri et al. [59]. Importantly, the model was also able to reproduce the kinetic data from an independent study by Nisimoto et al. [62], thereby further validating the predictive value of the model and also testing the mutual binding enhancements hypothesis (i.e. p67phox and Rac enhancing the binding of each other to Flavocytb558). Moreover, the same model was also able to reproduce all the kinetic data from Cross et al. [63,64] obtained using very different experimental conditions. Thus, we have extensively challenged our model with diverse experimental data [59–64] to obtain a reliable and predictive model of NOX2 assembly and activation.
Integrated computational modelling of ROS production and scavenging from different sources provides a plausible mechanistic and quantitative framework for understanding the kinetic/molecular mechanisms regulating ROS homeostasis within cells/tissues under different assay conditions. We have recently developed and parameterized several computational models in this manner characterizing the kinetic/molecular mechanisms for the production and scavenging of ROS in the mitochondria [78–81]. The current model complements our recent NOX2 model [71], which characterized the thermodynamics of electron transfer from NADPH to O2 through different redox centers of NOX2 complex (i.e. FAD and Cytb558 of Flavocytb558) upon its assembly and activation. This model captured the dependence of NOX2 activity upon pH and temperature variations, and the distinct inhibitory effects of different drugs (DPI and GSK) on NOX2 activity. As with the current model, it was based on diverse published data on NOX2 kinetics obtained from a diversity of experimental conditions [58,72–77]. That model, however, did not consider the kinetics and regulation of different cytosolic subunit concentration-dependent assembly and activation of NOX2 facilitating production, the focus of the current study.
The present NOX2 assembly and activation model is significant in several aspects. First, the model integrates the interactions of all the cytosolic subunits with the membrane subunits based on a unified/generalized random rapid equilibrium binding mechanism. In contrast, the existing experimental studies have evaluated the kinetics of NOX2 assembly and activation using only a few cytosolic subunits in a given experimental system. No unified hypothesis regarding NOX2 assembly and activation mechanism has yet been proposed. For example, Cross et al. [47] proposed a special binding mechanism for NOX2 assembly and activation. Their kinetic scheme considered first essential binding of the subunit p47phox to Flavocytb558, and then random ordered binding of the subunits p67phox and Rac to the complex. However, this scheme was unable to simulate the experimentally-measured changes in NOX2 activity ( production) when the cytosolic subunits concentrations were varied [59–64]. It was for this reason that we considered an alternative kinetic mechanism, namely the generalized random rapid equilibrium binding mechanism, for the cytosolic subunits to bind to the membrane subunits toward NOX2 assembly and activation (Figure 2). This enabled development of an integrated model of NOX2 assembly and activation which was able to simulate changes in the experimentally-measured NOX2 activity and production with respect to varying cytosolic subunits concentrations in diverse experimental systems [59–64].
Other examples demonstrate the validity of the generalized random rapid equilibrium binding mechanism of the current model. Specifically, the subunit p40phox was shown to be essential for NOX2 assembly and activation on the phagosomal membrane, but significantly less on the plasma membrane [55–57]. It was also found in cell-free systems that p40phox enhances NOX2 activity by primarily enhancing the binding affinity of p47phox for Flavocytb558 [64]. Remarkably, we were able to mathematically describe how p40phox enhances the binding affinity of p47phox for Flavocytb558 (Equation (3a)), which in turn enhances NOX2 activity. Although we did not consider p40phox was essential for NOX2 assembly and activation, the model can be easily extended as required to account for the p40phox requirements for NOX2 assembly and activation on the phagosomal membranes [55–57]. Importantly, the present model appears to explain how and why NOX2 assembly and activation differs in different assay systems as a consequence of differences in the magnitudes of the kinetic parameters (e.g. apparent binding constants; Tables 1 and 2). The differences in the estimated apparent binding constants may be attributed to different affinities of the enzyme (Flavocytb558) for the substrates (cytosolic subunits) as a consequence of varying molecular interactive forces between the enzyme and the substrates in these different assay systems.
A second important feature of the model is the regulatory control of NOX2 assembly and activation that accounts for the stimulatory and inhibitory interactions of guanine nucleotides (GTP and GDP) on the oxidase activation and subsequent production. Based on the kinetic data of Uhlinger et al. [60] and Peveri et al. [59], the model sheds light on the opposing effects of GTP and GDP on NOX2 activity and production. The model predictions suggest that 10 μM GTP is indeed required to maximally activate NOX2, while several orders of magnitude more GDP (>10 mM) is required to maximally inhibit NOX2. Moreover, there was an appreciable baseline NOX2 activity without any added GTP and GDP, due to the presence of ~0.5 μM baseline GTP (Figure 4). Furthermore, according to our model formulation, GTP not only enhances the binding of Rac to Flavocytb558, but also enhances the bindings of p47phox and p67phox to Flavocytb558, effectively enhancing the assembly and activation of NOX2 (Equation (3a–3c)). It is evident from the analysis that these events significantly affect the apparent kinetic parameters for these different cytosolic subunits binding to membrane Flavocytb558 (Figures 6–8).
Finally, the model accounted for a generalized mutual binding enhancement mechanism based on the studies of Uhlinger et al. [61] and Nisimoto et al. [62]. That is, the model simulated the influence of the subunits p47phox, p67phox and Rac upon each other’s binding to the membrane subunits gp91phox and p22phox (Flavocytb558) toward the oxidase activity (Figure 5 and Figures 6–8). Interestingly, the model predicted that the contribution of p47phox toward p67phox binding enhancement for Flavocytb558 is approximately 10-fold higher than the contribution of p67phox towards p47phox binding enhancement for Flavocytb558. The model also predicted that there is no mutual binding enhancement between p47phox and Rac, and only a negligible enhancement in the binding of Rac by p67phox, but a significant enhancement in the binding of p67phox by Rac (see Table 2). Overall, the model predicted that different cytosolic subunits differentially enhance the binding of the other cytosolic subunits to the membrane subunits in NOX2 assembly and activation characterized by different regulatory constants (see Table 2 and Appendix B).
Two sets of parameters are reported in Tables 1 and 2 corresponding to the two different types of datasets fitted to the model under different experimental conditions and protocols (i.e. Cross et al. [63,64] studies in fully recombinant cell-free systems vs. Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62] studies in semi-recombinant cell-free systems that included isolated plasma membrane). Cross et al. datasets were not suitable to characterize the regulatory mechanisms by guanine nucleotides (GTP and GDP) and mutual binding enhancements between the cytosolic subunits. This is because they varied only one subunit concentration while keeping all the other subunits and GTP at saturated concentrations in the absence of GDP. Thus, Equation (2) was only used to fit the datasets of Cross et al. In contrast, Equation (2) along with regulatory mechanisms incorporated into Equation (3a–3c) were used to jointly fit the datasets of Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62]. Based on our hybrid approach of Monte-Carlo–Fmincon simulations, we were able to obtain unique estimates of the model parameters characterizing each of these two distinct cell-free systems for NOX2 assembly and activation. For robust estimation of the model parameters, some parameters were assumed to be fixed, which are mentioned in the tables, determined from the experimental conditions/protocols (i.e. Flavocytb558 concentrations, baseline cytosolic subunits concentrations, baseline GTP and GDP concentrations, and Hill’s coefficients for regulation by GTP and GDP), and the rest of the parameters were left adjustable.
The logic behind fixing the baseline concentrations of Rac (for the experimental data of Uhlinger et al. [60]) and p47phox (for the experimental data of Nisimoto et al. [62]) at negligible levels is that, based on our model (Equation (2)), Rac and p47phox are essential for the assembly and activation of NOX2, yet these subunits were not added to the experimental protocols and assumed only to be present at negligible concentrations. Similarly, for some experiments of Uhlinger et al. [60], no GTP was added to the experimental protocol, yet significant baseline NOX2 activity was reported due to the presence of appreciable concentration of endogenous GTP, giving rise to about 50% of maximal NOX2 activity in the presence of high/saturable concentrations of GTP (10 μM). Thus, the baseline GTP concentration was fixed near the estimated KGTP value for NOX2 assembly and activation. The logic behind fixing the Hill’s coefficients for the enhancement of NOX2 assembly and activation by GTP at 2.0 and for the inhibition by GDP at 0.5 is that these values predict the accurate activation and inhibition profiles of NOX2 by GTP and GDP, respectively, as reported in Figure 4(C,D) without unnecessarily adding these parameters as unknown parameters for the estimation process. This enabled us to reduce the number of unknown parameters for estimation by two and also to break the correlation of these parameters with the regulatory constants for GTP and GDP (KGTP and KGDP) for NOX2 activation and inhibition, respectively. Thus, the estimates of the Hill’s coefficients are deduced from the experimental data on GTP and GDP-dependent regulation of NOX2 activity (Figure 4(C,D)). Adding these parameters to the estimation process also gives the similar estimates as fixed.
Limitations
We recognize that the actual molecular mechanism involving the assembly and activation of NOX2 complex (E.p47.p67.Rac) may be more sophisticated than what is represented in our model that utilized a generalized random rapid equilibrium binding mechanism involving 12 individual reactions and 3 apparent binding constants K′p47, K′p67 and K′Rac (Figure 2). We have mathematically lumped several important aspects of the regulation of NOX2 assembly and activation. Specifically, we have lumped the uncertainties of the quantitative details of the 12 reactions into the three apparent binding constants (K′p47, K′p67 and K′Rac) for the cytosolic subunits for the membrane subunits and the apparent catalytic constant for NOX2 (kNOX2). These three binding constants were further related to the concentrations of the cytosolic subunits and the concentrations of GTP and GDP (Equation (3a–3c)), which enabled predictive simulations of an array of kinetic data from six different publications from four independent groups [59–64]. Consistent with the process of model building, the future iterations of this model can incorporate more details of the protein–protein interaction reactions, phosphorylation and dephosphorylation, alternative NOX2 assembly and activation mechanisms, and the regulation of the assembly and activation process by the Rho/Rac GTPase regulation cycle, as appropriate quantitative kinetic data becomes available.
An alternative assumption with the same random rapid equilibrium binding mechanism might be that the 12 individual reactions are characterized by 12 apparent binding constants K′p47.n, K′p67.n and K′Rac.n, n = 1 … 4, satisfying 6 kinetic constraints involving the 6 rectangular surfaces of Figure 2 (6 microscopic balance constraints). So, without further simplification, this assumption leads to an increase in the number of unknown parameters in the model. In addition, one of the possible outcomes of this alternative assumption is that all the four apparent binding constants for each subunit may be equal. To illustrate this, consider the formation of the intermediate complex E.p47.p67 through the two different reaction sequences described above with the apparent binding constants K′p47.1, K′p47.2, K′p67.1, and K′p67.2. To satisfy the microscopic balance constraint, we must have K′p47.1 × K′p67.2 = K′p67.1 × K′p47.2 (since both reaction sequences result in the same intermediate complex E.p47.p67). But this kinetic constraint indicates that both p47phox and p67phox would enhance the binding of each other to the same extent, which is not the case as illustrated through the results presented in Figures 6–7. Another possible outcome is that K′p47.1 = K′p47.2 and K′p67.1 = K′p67.2. The same analogy can be applied to the other intermediate complexes and the final NOX2 enzyme complex E.p47.p67.Rac to arrive at the same conclusion that all of the four apparent binding constants for each subunit may be equal. This assumption satisfies the microscopic and the overall balance constraints. The apparent binding constants are further functions of GTP, GDP, p47, p67, and Rac concentrations for the model to be able to describe all of the diverse experimental data simultaneously (Equation (3a–3c)). Therefore, we believe the ability of the developed model with hypothesized kinetic/regulation mechanisms to describe six different datasets [59–64] produced by four different groups is sufficient to ascertains the accuracy and the reliability of the model and kinetic/regulation mechanisms in describing the biological process of production on the cell membrane through the assembled and activated NOX2 complex.
Another limitation in our model is that the binding of the cytosolic subunits to the membrane subunits in forming the stable NOX2 complex in catalysing production may not all be rapidly equilibrating or even randomly ordered. The NOX2 assembly reactions in vivo may all be rate limiting. However, we analyzed kinetic data from several publications [59–64], and we were able to reproduce all the data with our model applying the generalized random rapid equilibrium binding assumption for NOX2 assembly and activation. This suggests that these data may not have sufficient information to evaluate the validity of such an assumption for computational modelling. We think that in vivo the slow or rate limiting nature of the assembly reactions in cells may lead to reduced concentrations of the stable NOX2 complex in catalyzing production, which can be effectively accounted for by suitably reducing the catalytic constant (kNOX2) for the production reaction or by suitably reducing the availability of the membrane subunit (E0), without affecting the apparent binding constants (K′s) for NOX2 assembly reactions. Another possibility would be to consider all the reactions involving NOX2 assembly (Figure 2) as rate limiting. But then this would lead to myriad of unknown parameters (twice the number of rate constants than binding constants) that would need to be estimated from the available data resulting in a model that would not be minimal or parsimonious and would have little predictive value. The publications [59–64] used in this modeling work as sources for the kinetic data, although in themselves are robust and rigorous, were conducted at a time when the components and assembly of NOX2 were less well understood, and consequently some of the components and their variations used in those studies may not completely fit with modern experimental approaches. On the other hand, the dearth of recent experimental studies providing amenable kinetic data means these are the best sources of data for further development of the model. This will enable more practical model based on current understanding of NOX2 assembly and activation.
Summary
A detailed mechanistic computational model was developed that incorporates diverse kinetic and regulatory mechanisms required for the assembly and activation of NOX2 facilitating production. The model accounts for the mutual interdependencies of NOX2 cytosolic subunits on NOX2 assembly and activation as well as regulations by guanine nucleotides. The model is capable of explaining kinetic data from diverse experimental systems with model simulations indicating that: (i) cytosolic subunits follow a random rapid equilibrium binding mechanism with their membrane counterparts towards NOX2 assembly and activation; (ii) guanine nucleotides are important regulators of NOX2 assembly and activation; (iii) cytosolic subunits p47phox, p67phox and Rac differentially enhance the binding of one another’s, with p47phox enhancing the binding affinity of p67phox an order of magnitude higher than p47phox enhancing the binding affinity of p67phox to the membrane subunits; (iv) Rac differentially enhances the binding affinity of p47phox and p67phox to the membrane subunits; (v) there is no mutual binding enhancement between p47phox and Rac; and (vi) p40phox enhances the binding affinity of p47phox to the membrane subunits, further enhancing NOX2 assembly and activation. The model therefore provides a mechanistic and quantitative framework to investigate the differential roles of different NOX2 subunits on its assembly and activation on the cell membrane facilitating production regulating diverse cellular mechanisms in a variety of conditions. The model also serves as a quantitative structure to expand upon in ways that would incorporate such concepts as membrane NOX and mitochondrial ROS-ROS crosstalk and interactions as encountered in conditions of health and disease. Ultimately, there is also a need for better quantitative kinetic data based on current understanding of NOX2 assembly and activation in order to test and further advance this mode
Funding
This work was supported by the National Institute of Health (NIH) grants P01-GM066730, P01-HL116264, and U01-HL122199.
Appendix A
This Appendix provides the mathematical derivation for the cytosolic subunits (p47phox, p67phox, and Rac)-dependent NOX2 complex formation and reaction flux expression under the condition of high (saturating) concentrations of the substrates NADPH and O2 governed by the biochemical reaction: . Electron transfer from the substrate NADPH to O2 occurs upon NOX2 assembly and activation, as depicted in Figure 2, in which p40phox is not considered essential for NOX2 assembly and activation.
In addition, the proposed mechanism for NOX2 assembly and activation is based on random rapid equilibrium binding of the cytosolic subunits p47phox, p67phox, and Rac to the membrane components gp91phox and p22phox (complexed as E = gp91phox.p22phox), as described by the following elementary reactions:
| (A1a) |
| (A1b) |
| (A1c) |
| (A1d) |
| (A1e) |
| (A1f) |
| (A1g) |
| (A1h) |
| (A1i) |
| (A1j) |
| (A1k) |
| (A1l) |
where K′ s are the apparent dissociation/binding constants. Based on rapid equilibrium binding assumption, we have the following equilibrium relationships:
| (A2a) |
| (A2b) |
| (A2c) |
| (A2d) |
| (A2e) |
| (A2f) |
| (A2g) |
The total NOX2 enzyme concentration is given by:
| (A3) |
By substituting the expressions for the concentrations of different enzyme complexes from Equation (A2(a–g)) into Equation (A3), we have:
| (A4) |
This gives the expression for the free NOX2 enzyme concentration in terms of the total NOX2 enzyme concentration and the concentrations of different cytosolic NOX2 subunits:
| (A5) |
Now, by substituting [E] from Equation (5A) into Equation (A2g), we can express the concentration of the total assembled and activated NOX2 complex as:
| (A6) |
Now, by multiplying the numerator and denominator of Equation (A6) by K′p47 K′p67K′Rac and factoring out , and in separate steps, Equation (A6) can be simplified to:
| (A7) |
At high (saturating) concentrations of the substrates NADPH and O2, the overall NOX2 reaction flux is proportional to [E.p47.p67.Rac], and hence can be expressed as:
| (A8) |
where kNOX2 is NOX2 catalytic constant at high NADPH and O2 concentrations. At limiting or sub-saturating concentrations of the substrates NADPH and O2, NOX2 catalytic constant kNOX2 would be a function of [NADPH] and [O2], as developed in our recent publication [71].
Appendix B
This Appendix provides information on how the regulatory effects of guanine nucleotides (GTP, GDP) and cytosolic subunits (p40phox, p47phox, p67phox, and Rac) on NOX2 reaction flux were implemented in Equation (A8) to develop the final model presented in Equations (2), (3a), (3b), and (3c). This required the following steps: first, only the regulatory effects of guanine nucleotides were included resulting in Model 1; second, the regulatory effects of the same extent mutual binding enhancements between cytosolic subunits were implemented in Model 1 resulting in Model 2; third, the regulatory effects of the different extent mutual binding enhancements between cytosolic subunits were implemented in Model 1 resulting in Model 3. Each subsequent model, which is a nested version of the previous model, has more unknown parameters compared to the previous model, resulting in a better fit of the model to the experimental datasets. We also performed statistical tests, such as the F-test and the Akaike’s information criterion (AIC) to compare the performance of Model 3 with its nested version (Model 2) and prove its superior fittings to the pertinent datasets. A hybrid approach of Monte-Carlo simulations and “fmincon” optimizer in MATLAB for parameter estimation is used in addition to computing the correlation coefficient matrix (CCM) to obtain the degree of interdependence between the model parameters.
Model 1: Regulations of cytosolic subunits binding by guanine nucleotides, without any mutual binding enhancements.
In this model, the regulatory effects of guanine nucleotides (GTP, GDP) are accounted for. As mentioned in the main text, based on the experimental data of Uhlinger et al. [60], GTP enhances the binding of cytosolic subunits (p47phox, p67phox, and Rac) to the membrane subunits (p22phox and gp91phox), while GDP inhibits the binding of these cytosolic subunits. These regulatory effects are implemented by phenomenologically expressing the apparent binding constants , , and based on the standard Michaelis-Menten kinetic formulation for activation by GTP and inhibition by GDP as following:
| (B1) |
| (B2) |
| (B3) |
where CGTP and CGDP denote the concentrations of GTP and GDP, respectively; KGTP and KGDP denote the regulatory constants for GTP and GDP to enhance and inhibit NOX2 activity, respectively; nT and nD are the corresponding Hill coefficients. This model (Model 1), without any mutual binding enhancements, was used to fit jointly to the experimental datasets of Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62] to estimate the unknown parameters of the model. However, it was not able to describe well these datasets without any mutual binding enhancements by cytosolic subunits, resulting in a large sum of squared differences error of 7.54, obtained by the “fmincon” optimization algorithm in MATLAB 2018b.
Model 2: Same extent mutual binding enhancements between cytosolic subunits (each subunit enhancing the binding of other subunits to the same extent).
In order to improve the model fits and reduce the sum of squared differences error from the model fittings to the available experimental data described above, we accounted for the regulatory effects of cytosolic subunits (p47phox, p67phox, and Rac) on one another’s binding to the membrane subunits (p22phox and gp91phox). As described in the main texts, based on Uhlinger et al. [61] studies, binding of p47phox enhances the binding of p67phox to the membrane subunits and vice versa (mutual binding enhancement), which we hypothesized to exist between all three cytosolic subunits (p47phox, p67phox, and Rac) for the sake of generality. To account for this mutual binding enhancement mechanism in the model, we assumed that p47phox binding enhances p67phox binding to the membrane subunits to the same extent as p47phox binding enhances Rac binding to the membrane subunits, referred here as the same extent mutual binding enhancement hypothesis, which is accounted for in the binding constants , , and as following:
| (B4) |
| (B5) |
| (B6) |
where K″p47, K″p67 and K″Rac are the regulatory constants for p47phox, p67phox and Rac, respectively, characterizing the regulations of each other’s binding to Flavocytb558; Cp47 and Cp67 and CRac are the concentrations of p47phox, p67phox and Rac, respectively. This model (Model 2) was used to fit jointly to the experimental datasets by Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62] to estimate the unknown parameters of the model. It was able to describe the datasets by Uhlinger et al. and Peveri et al. on the GTP and GDP regulatory effects and cytosolic subunits mutual binding enhancements, but not the datasets by Nisimoto et al. on the cytosolic subunits mutual binding enhancements with the sum of squared differences error of 5.85, obtained by the “fmincon” optimization algorithm in MATLAB 2018 b.
Table B1.
Statistical comparison between Model 2 and Model 3 through F-test, fitted jointly to the experimental data of Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62].
| Model | SSD | Number of parameters | Number of data points | DF | F ratio | p Value |
|---|---|---|---|---|---|---|
| 2 | 5.85 | 9 | 176 | 167 | 51.58 | <0.0001 |
| 3 | 3.01 | 12 | 176 | 164 |
Figure B1.

Distribution of Model 2 estimated parameter values based on a hybrid Monte-Carlo-Fmincon simulations method. Plots show the distribution of the 9 estimated unknown parameter values for Model 2 fitted to experimental data of Uhlinger et al. [60, 61], Peveri et al. [59], and Nisimoto et al. [62] using a hybrid approach of Monte-Carlo simulations and “fmincon” optimization algorithm in MATLAB. The model is provided with 10,000 sets of 9 random initial values between 0 and 1 and the unknown parameters are estimated by “fmincon” optimizer for every set resulting in the values with the most probability of occurrence. For every parameter, the value with more than 55% probability of occurrence is indicated via the highest histogram bars that are also reported as the final estimated parameter values in Table 2. In this model, Kp67 is fixed at 0.05 μM and the rest of parameters are estimated.
Figure B2.
Distribution of Model 3 estimated parameter values based on a hybrid Monte-Carlo–Fmincon simulations method. Plots show the distribution of the 12 estimated unknown parameter values for Model 3 fitted to the experimental data of Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62] using a hybrid approach of Monte-Carlo simulations and “fmincon” optimization algorithm in MATLAB. The model is provided with 10,000 sets of 12 random initial values between 0 and 1 and the unknown parameters are estimated by “fmincon” optimizer for every set resulting in the values with the most probability of occurrence. For every parameter, the value with more than 55% probability of occurrence is indicated via the highest histogram bars that are also reported as the final estimated parameter values in Table 2.
Model 3: Different extent mutual binding enhancements between cytosolic subunits.
Based on the fits using Model 2, it was clear that the extent to which p47phox enhances the binding of p67phox is not the same as p67phox enhancing the binding of p47phox to the membrane subunits, which is true for all three cytosolic subunits. This difference provides the basis to further improve Model 2 by allowing for differential mutual binding enhancements between cytosolic subunits as following:
| (B7) |
| (B8) |
| (B9) |
where K″p67p47 and K″Racp47 are the regulatory constants for the p47phox binding enhancements by p67phox and Rac, respectively; K″p47p67 and K″Racp67 are the regulatory constants for the p67phox binding enhancements by p47phox and Rac, respectively; and K″p47Rac and K″p67Rac are the regulatory constants for the Rac binding enhancements by p47phox and p67phox, respectively. The resulting model (Model 3) was used to fit jointly to the experimental datasets by Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62] to estimate the unknown parameters of the model. Model 3 was able to describe all the datasets on GTP and GDP regulatory effects as well as cytosolic subunits mutual binding enhancements with a very small sum of squared differences error of 3.01, obtained by the “fmincon” optimization algorithm in MATLAB 2018 b.
Figure B3.

Matrix of correlation coefficients between Model 2 parameters: The correlation coefficients between Model 2 parameters from Table 2 that best fit the model to the data is obtained using the “lsqcurvefit” algorithm. The correlation coefficients are in the range of −1 to +1 indicated with red color showing positive correlation in the range of 0 to +1; the blue color showing negative correlation in the range of 0 to −1; and the darker colors show higher correlation close to either ±1. The diagonal of the matrix shows the correlation of each parameter with itself which is 1. Also, since the matrix is symmetric, the upper triangle is put values equal to 0 for simplicity. Small correlation coefficients show small interdependence between the model parameters. In this model, Kp67 is fixed and its correlation with other parameters cannot be calculated, and hence is removed.
Regulatory effect of p40phox on p47phox binding.
Based on the experimental datasets published by Cross et al. [64], p40phox participates in activating NOX2 primarily by enhancing the binding affinity of p47phox to the membrane subunits. This regulatory effect is accounted for via p47phox binding affinity, as described in Equation (3a), to fit the model to the datasets by Cross et al. in which p40phox is present. In order to fit the same model to Uhlinger et al. [60,61], Peveri et al. [59], and Nisimoto et al. [62] datasets in which p40phox was not present, the last term in Equation (3a) is set to 1 (i.e. Cp40 = 0). Hence, the same model is able to describe and fit different datasets under different experimental conditions such as cell-free and reconstituted cell-based systems.
Comparison of the model fits for the three models.
Model 3 provided a better fit to the datasets (Figures 3, 4 and 5) than Model 2, resulting in a smaller sum of squared differences error. This is not surprising since Model 2 is a nested version of Model 3, and hence Model 3 has more unknown parameters. To determine whether the improvement in the fit using Model 3 as compared to the fit using Model 2 is large enough to justify the larger number of unknown parameters, we performed an F-test (Equation (B10)):
| (B10) |
where SSD2 and SSD3 are the sum of squared differences between data and Model 2 fit and Model 3 fit, respectively; DF2 and DF3 are the degrees of freedom for Model 2 and Model 3, respectively [82]. P value is the probability of null hypothesis to be correct with significance level (p = 0.05; 95% confidence). Thus, the F-test takes into account the sum of squared differences, number of model parameters, and number of data points to compare two models and determine whether Model 3 is statistically a better model for the data in Figures 3, 4 and 5 than Model 2 [82]. Based on F-test for Model 2 and Model 3 in Table B1, the P value is less than 0.05 showing that the alternative hypotheses on Model 3 providing a significantly better fit than Model 2 is correct.
Figure B4.

Matrix of correlation coefficients between Model 3 parameters. The correlation coefficients between Model 3 parameters from Table 2 that best fit the model to the data is obtained using the “lsqcurvefit” algorithm. The correlation coefficients are in the range of −1 to +1 indicated with red color showing positive correlation in the range of 0 to +1; the blue color showing negative correlation in the range of 0 to −1; and the darker colors show higher correlation close to either ±1. The diagonal of the matrix shows the correlation of each parameter with itself which is 1. Also, since the matrix is symmetric, the upper triangle is put values equal to 0 for simplicity. Small correlation coefficients show small interdependence between the model parameters.
In the case of having two nested models, F-test is the proper test to compare the two models. However, AIC method is used for two or more number of nested and/or unrelated models. We also performed AIC test to compare the two models statistically based on Equation (B11):
| (B11) |
where N is the number of data points, K is the number of parameters, and SSD is the sum of squared differences for each model. The model with lower AIC is more likely to be correct. Based on the AIC values in Table 2, Model 3 is superior to Model 2. Therefore, based on both F-test and AIC results, Model 3 provides a significantly better fit to the pertinent data than Model 2. The fit of Model 1 to the data was visually bad enough that we did not attempt to compare it to that using Model 3.
Parameter estimation via hybrid Monte-Carlo–Fmincon simulations.
In order to estimate the unknown parameters of the three models, we used a hybrid approach of Monte-Carlo simulations and “fmincon” optimization algorithm. In doing this, we provided the model with 10,000 sets of random initial values uniformly distributed between 0 and 1 with the mean of 0.5 and standard deviation of 0.28. Using one set of random initial values, provided by the built-in “rand” function in MATLAB, the unknown parameters are estimated via the “fmincon” optimizer by minimizing the sum of squared differences between model simulations and data points resulting in one set of estimated parameters. This procedure was repeated for 10,000 iterations and the global estimates of the unknown parameters were those with the highest probability of occurrence. Figure B1 shows the distribution of Model 2 estimated parameters using this approach in which K′p67 was fixed at 0.05 and the rest of the 8 parameters were estimated. Figure B2 shows the distribution of Model 3 estimated parameters using the aforementioned approach in which all 12 parameters were estimated. The final parameters with the global least of the sum of squared differences are indicated in the histogram bars with highest frequency showing the highest probability of occurrence.
Correlation coefficient matrix.
The correlation coefficients (CCij) between the model parameters that best fit the model to the data were obtained using Equation (B12):
| (B12) |
where N is the number of model parameters and HH is the inverse of the product of Jacobian matrix and its transpose. Figures B3 and B4 show the correlation coefficient matrices for Model 2 and Model 3, respectively, obtained from the estimated parameter values in Table 2. Based on Model 2 correlation coefficient matrix, kNOX2 has high correlation with KRac and , and KRac has high correlation with and . Also, based on Model 3 correlation coefficient matrix, kNox2 has high correlation with KRac, and ; KRac has high correlation with and ; and Kp67 has high correlation with , all of which were expected based on the interdependency of these parameters in Equations (B7–B9). However, for both the models, the correlation coefficients between several parameters are relatively small, indicating their independency of each other and their identifiability and estimability.
Footnotes
Disclosure statement
No potential conflict of interest was reported by the author(s).
References
- [1].Murphy MP. How mitochondria produce reactive oxygen species. Biochem J. 2009;417(1):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Stowe DF, Camara AK. Mitochondrial reactive oxygen species production in excitable cells: modulators of mitochondrial and cell function [invited comprehensive review]. Antioxid Redox Signal. 2009; 11(6):1373–1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Figueira TR, Barros MH, Camargo AA, et al. Mitochondria as a source of reactive oxygen and nitrogen species: from molecular mechanisms to human health. Antioxid Redox Signal. 2013;18(16): 2029–2074. [DOI] [PubMed] [Google Scholar]
- [4].Lacy F, Gough DA, Schmid-Schönbein GW. Role of xanthine oxidase in hydrogen peroxide production. Free Radic Biol Med. 1998;25(6):720–727. [DOI] [PubMed] [Google Scholar]
- [5].Berry CE, Hare JM. Xanthine oxidoreductase and cardiovascular disease: molecular mechanisms and pathophysiological implications. J Physiol. 2004;555(Pt 3):589–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kelley EE, Khoo NK, Hundley NJ, et al. Hydrogen peroxide is the major oxidant product of xanthine oxidase. Free Radic Biol Med. 2010;48(4):493–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Bokoch GM, Knaus UG. NADPH oxidases: not just for leukocytes anymore!. Trends Biochem Sci. 2003;28(9): 502–508. [DOI] [PubMed] [Google Scholar]
- [8].Lambeth JD. NOX enzymes and the biology of reactive oxygen. Nat Rev Immunol. 2004;4(3):181–189. [DOI] [PubMed] [Google Scholar]
- [9].Brandes RP, Kreuzer J. Vascular NADPH oxidases: molecular mechanisms of activation. Cardiovasc Res. 2005;65(1):16–27. [DOI] [PubMed] [Google Scholar]
- [10].Bedard K, Krause KH. The NOX family of ROS-generating NADPH oxidases: physiology and pathophysiology. Physiol Rev. 2007;87(1):245–313. [DOI] [PubMed] [Google Scholar]
- [11].Brandes RP, Weissmann N, Schroder K. Nox family NADPH oxidases: molecular mechanisms of activation. Free Radic Biol Med. 2014;76:208–226. [DOI] [PubMed] [Google Scholar]
- [12].Lambeth JD, Neish AS. Nox enzymes and new thinking on reactive oxygen: a double-edged sword revisited. Annu Rev Pathol. 2014;9:119–145. [DOI] [PubMed] [Google Scholar]
- [13].Bhattacharyya A, Chattopadhyay R, Mitra S, et al. Oxidative stress: an essential factor in the pathogenesis of gastrointestinal mucosal diseases. Physiol Rev. 2014;94(2):329–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Bokoch GM. Regulation of innate immunity by Rho GTPases. Trends Cell Biol. 2005;15(3):163–171. [DOI] [PubMed] [Google Scholar]
- [15].Kohchi C, Inagawa H, Nishizawa T, et al. ROS and innate immunity. Anticancer Res. 2009;29(3):817–821. [PubMed] [Google Scholar]
- [16].Bae YS, Oh H, Rhee SG, et al. Regulation of reactive oxygen species generation in cell signaling. Mol Cells. 2011;32(6):491–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Ray PD, Huang BW, Tsuji Y. Reactive oxygen species (ROS) homeostasis and redox regulation in cellular signaling. Cell Signal. 2012;24(5):981–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Brown DI, Griendling KK. Regulation of signal transduction by reactive oxygen species in the cardiovascular system. Circ Res. 2015;116(3):531–549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Yarosz EL, Chang CH. The role of reactive oxygen species in regulating T cell-mediated immunity and disease. Immune Netw. 2018;18(1):e14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Brown DI, Griendling KK. Nox proteins in signal transduction. Free Radic Biol Med. 2009;47(9):1239–1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Carvalho DP, Dupuy C. Role of the NADPH oxidases DUOX and NOX4 in thyroid oxidative stress. Eur Thyroid J. 2013;2(3):160–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Singel KL, Segal BH. NOX2-dependent regulation of inflammation. Clin Sci (Lond)). 2016;130(7):479–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Lassegue B, Griendling KK. NADPH oxidases: functions and pathologies in the vasculature. Arterioscler Thromb Vasc Biol. 2010;30(4):653–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Al Ghouleh I, Khoo NK, Knaus UG, et al. Oxidases and peroxidases in cardiovascular and lung disease: new concepts in reactive oxygen species signaling. Free Radic Biol Med. 2011;51(7):1271–1288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Sedeek M, Nasrallah R, Touyz RM, et al. NADPH oxidases, reactive oxygen species, and the kidney: friend and foe. J Am Soc Nephrol. 2013;24(10):1512–1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Meitzler JL, Antony S, Wu Y, et al. NADPH oxidases: a perspective on reactive oxygen species production in tumor biology. Antioxid Redox Signal. 2014;20(17): 2873–2889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Thallas-Bonke V, Jandeleit-Dahm KA, Cooper ME. Nox4 and progressive kidney disease. Curr Opin Nephrol Hypertens. 2015;24(1):74–80. [DOI] [PubMed] [Google Scholar]
- [28].Audi SH, Friedly N, Dash RK, et al. Detection of hydrogen peroxide production in the isolated rat lung using Amplex red. Free Radic Res. 2018;52(9):1052–1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Takac I, Schroder K, Zhang L, et al. The E-loop is involved in hydrogen peroxide formation by the NADPH oxidase Nox4. J Biol Chem. 2011;286(15): 13304–13313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Segal AW. The function of the NADPH oxidase of phagocytes and its relationship to other NOXs in plants, invertebrates, and mammals. Int J Biochem Cell Biol. 2008;40(4):604–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Paffenholz R, Bergstrom RA, Pasutto F, et al. Vestibular defects in head-tilt mice result from mutations in Nox3, encoding an NADPH oxidase. Genes Dev. 2004; 18(5):486–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Holterman CE, Thibodeau JF, Kennedy CR. NADPH oxidase 5 and renal disease. Curr Opin Nephrol Hypertens. 2015;24(1):81–87. [DOI] [PubMed] [Google Scholar]
- [33].Zheleznova NN, Yang C, Cowley AW. Jr., Role of Nox4 and p67phox subunit of Nox2 in ROS production in response to increased tubular flow in the mTAL of Dahl salt-sensitive rats. Am J Physiol Renal Physiol. 2016;311(2):F450–F458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Cowley AW Jr.,Yang C, Zheleznova NN, et al. Evidence of the importance of Nox4 in production of hypertension in Dahl salt-sensitive rats. Hypertension. 2016; 67(2):440–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Touyz RM, Anagnostopoulou A, Camargo LL, et al. Vascular biology of superoxide-generating NADPH oxidase 5-implications in hypertension and cardiovascular disease. Antioxid Redox Signal. 2019;30(7): 1027–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Martner A, Aydin E, Hellstrand K. NOX2 in autoimmunity, tumor growth and metastasis. J Pathol. 2019; 247(2):151–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].van der Weyden L, Speak AO, Swiatkowska A, et al. Pulmonary metastatic colonisation and granulomas in NOX2-deficient mice. J Pathol. 2018;246(3):300–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].El-Benna J, Dang PM-C, Gougerot-Pocidalo M-A, et al. Francoise Braut-Boucher, p47phox, the phagocyte NADPH oxidase/NOX2 organizer: structure, phosphorylation and implication in diseases. Exp Mol Med. 2009;41(4):217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Juan D Matute AAA, Wright NAM, Wrobel I, et al. A new genetic subgroup of chronic granulomatous disease with autosomal recessive mutations in p40 phox and selective defects in neutrophil NADPH oxidase activity. Blood. 2009;114(15):3309–3315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Bromberg Y, Pick E. Unsaturated fatty acids stimulate NADPH-dependent superoxide production by cell-free system derived from macrophages. Cell Immunol. 1984;88(1):213–221. [DOI] [PubMed] [Google Scholar]
- [41].Bromberg Y, Pick E. Activation of NADPH-dependent superoxide production in a cell-free system by sodium dodecyl sulfate. J Biol Chem. 1985;260(25): 13539–13545. [PubMed] [Google Scholar]
- [42].Koshkin V, Pick E. Generation of superoxide by purified and relipidated cytochrome b559 in the absence of cytosolic activators. FEBS Lett. 1993;327(1):57–62. [DOI] [PubMed] [Google Scholar]
- [43].Koshkin V, Pick E. Superoxide production by cytochrome b559. Mechanism of cytosol-independent activation. FEBS Lett. 1994;338(3):285–289. [DOI] [PubMed] [Google Scholar]
- [44].Koshkin V, Lotan O, Pick E. Electron transfer in the superoxide-generating NADPH oxidase complex reconstituted in vitro. Biochim Biophys Acta. 1997; 1319(2–3):139–146. [DOI] [PubMed] [Google Scholar]
- [45].Freeman JL, Lambeth JD. NADPH oxidase activity is independent of p47phox in vitro. J Biol Chem. 1996; 271(37):22578–22582. [DOI] [PubMed] [Google Scholar]
- [46].Cross AR, Curnutte JT. The cytosolic activating factors p47phox and p67phox have distinct roles in the regulation of electron flow in NADPH oxidase. J Biol Chem. 1995;270(12):6543–6548. [DOI] [PubMed] [Google Scholar]
- [47].Cross AR, Erickson RW, Curnutte JT. Simultaneous presence of p47(phox) and Flavocytochrome b-245 are required for the activation of NADPH oxidase by anionic amphiphiles. Evidence for an intermediate state of oxidase activation. J Biol Chem. 1999;274(22): 15519–15525. [DOI] [PubMed] [Google Scholar]
- [48].Dang PM, Cross AR, Quinn MT, et al. Assembly of the neutrophil respiratory burst oxidase: a direct interaction between p67PHOX and cytochrome b558 II. Proc Natl Acad Sci USA. 2002;99(7):4262–4265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Lapouge K, Smith SJM, Groemping Y, et al. Architecture of the p40-p47-p67phox complex in the resting state of the NADPH oxidase. A central role for p67phox, The. J Biol Chem. 2002;277(12):10121–10128. [DOI] [PubMed] [Google Scholar]
- [50].Quinn MT, Evans T, Loetterle LR, et al. Translocation of Rac correlates with NADPH oxidase activation. Evidence for equimolar translocation of oxidase components. J Biol Chem. 1993;268(28):20983–20987. [PubMed] [Google Scholar]
- [51].Heyworth PG, Bohl BP, Bokoch GM, et al. Rac translocates independently of the neutrophil NADPH oxidase components p47phox and p67phox. Evidence for its interaction with Flavocytochrome b558. J Biol Chem. 1994;269(49):30749–30752. [PubMed] [Google Scholar]
- [52].Ago T, Kuribayashi F, Hiroaki H, et al. Phosphorylation of p47phox directs phox homology domain from SH3 domain toward phosphoinositides, leading to phagocyte NADPH oxidase activation. Proc Natl Acad Sci USA. 2003;100(8):4474–4479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Groemping Y, Lapouge K, Smerdon SJ, et al. Molecular basis of phosphorylation-induced activation of the NADPH oxidase. Cell. 2003;113(3):343–355. [DOI] [PubMed] [Google Scholar]
- [54].Nauseef WM. Assembly of the phagocyte NADPH oxidase. Histochem Cell Biol. 2004;122(4):277–291. [DOI] [PubMed] [Google Scholar]
- [55].Belambri SA, Rolas L, Raad H, et al. NADPH oxidase activation in neutrophils: Role of the phosphorylation of its subunits. Eur J Clin Invest. 2018;48 Suppl 2: e12951. [DOI] [PubMed] [Google Scholar]
- [56].Tamura M, Shiozaki I, Ono S, et al. p40phox as an alternative organizer to p47phox in Nox2 activation: a new mechanism involving an interaction with p22phox. FEBS Lett. 2007;581(23):4533–4538. [DOI] [PubMed] [Google Scholar]
- [57].Li XJ, Marchal CC, Stull ND, et al. p47phox Phox homology domain regulates plasma membrane but not phagosome neutrophil NADPH oxidase activation. J Biol Chem. 2010;285(45):35169–35179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Suzuki Y, Lehrer RI. NAD(P)H oxidase activity in human neutrophils stimulated by phorbol myristate acetate. J Clin Invest. 1980;66(6):1409–1418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Peveri P, Heyworth PG, Curnutte JT. Absolute requirement for GTP in activation of human neutrophil NADPH oxidase in a cell-free system: role of ATP in regenerating GTP. Proc Natl Acad Sci USA. 1992;89(6): 2494–2498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Uhlinger DJ, Tyagi SR, Inge KL, et al. The respiratory burst oxidase of human neutrophils. Guanine nucleotides and arachidonate regulate the assembly of a multicomponent complex in a semirecombinant cell-free system. J Biol Chem. 1993;268(12):8624–8631. [PubMed] [Google Scholar]
- [61].Uhlinger DJ, Taylor KL, Lambeth JD. p67-phox enhances the binding of p47-phox to the human neutrophil respiratory burst oxidase complex. J Biol Chem. 1994; 269(35):22095–22098. [PubMed] [Google Scholar]
- [62].Nisimoto Y, Freeman JL, Motalebi SA, et al. Rac binding to p67(phox). Structural basis for interactions of the Rac1 effector region and insert region with components of the respiratory burst oxidase. J Biol Chem. 1997;272(30):18834–18841. [DOI] [PubMed] [Google Scholar]
- [63].Cross AR, Erickson RW, Curnutte JT. The mechanism of activation of NADPH oxidase in the cell-free system: the activation process is primarily catalytic and not through the formation of a stoichiometric complex, Biochem J. 1999;341(2):251–255. [PMC free article] [PubMed] [Google Scholar]
- [64].Cross AR. p40(phox) Participates in the activation of NADPH oxidase by increasing the affinity of p47(phox) for Flavocytochrome b(558). Biochem J. 2000;349(Pt 1): 113–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Bokoch GM, Bohl BP, Chuang TH. Guanine nucleotide exchange regulates membrane translocation of Rac/Rho GTP-binding proteins. J Biol Chem. 1994;269(50): 31674–31679. [PubMed] [Google Scholar]
- [66].Bokoch GM. Regulation of the human neutrophil NADPH oxidase by the Rac GTP-binding proteins. Curr Opin Cell Biol. 1994;6(2):212–218. [DOI] [PubMed] [Google Scholar]
- [67].Bokoch GM, Knaus UG. The role of small GTP-binding proteins in leukocyte function. Curr Opin Immunol. 1994;6(1):98–105. [DOI] [PubMed] [Google Scholar]
- [68].Gorzalczany Y, Sigal N, Itan M, et al. Targeting of Rac1 to the Phagocyte Membrane Is Sufficient for the Induction of NADPH Oxidase Assembly. J Biol Chem. 2000;275(51):40073–40081. [DOI] [PubMed] [Google Scholar]
- [69].Ugolev Y, Berdichevsky Y, Weinbaum C, et al. Dissociation of Rac1(GDP).RhoGDI complexes by the cooperative action of anionic liposomes containing phosphatidylinositol 3,4,5-trisphosphate, Rac guanine nucleotide exchange factor, and GTP. J Biol Chem. 2008;283(32):22257–22271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Pick E Role of the Rho GTPase Rac in the activation of the phagocyte NADPH oxidase: outsourcing a key task. Small GTPases. 2014;5:e27952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Tomar N, Sadri S, Cowley AW Jr, et al. A thermodynamically-constrained mathematical model for the kinetics and regulation of NADPH oxidase 2 complex-mediated electron transfer and superoxide production. Free Radic Biol Med. 2019;134:581–597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Babior BM, Curnutte JT, McMurrich BJ. The particulate superoxide-forming system from human neutrophils. Properties of the system and further evidence supporting its participation in the respiratory burst. J Clin Invest. 1976;58(4):989–996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Bauldry SA, Nasrallah VN, Bass DA. Activation of NADPH oxidase in human neutrophils permeabilized with Staphylococcus aureus alpha-toxin. A lower Km when the enzyme is activated in situ. J Biol Chem. 1992;267(1):323–330. [PubMed] [Google Scholar]
- [74].Morgan D, Cherny VV, Murphy R, et al. Temperature dependence of NADPH oxidase in human eosinophils. J Physiol. 2003;550(Pt 2):447–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Morgan D, Cherny VV, Murphy R, et al. The pH dependence of NADPH oxidase in human eosinophils. J Physiol. 2005;569(Pt 2):419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Nisimoto Y, Diebold BA, Cosentino-Gomes D, et al. Nox4: a hydrogen peroxide-generating oxygen sensor. Biochemistry. 2014;53(31):5111–5120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Hirano K, Chen WS, Chueng AL, et al. Discovery of GSK2795039, a Novel Small Molecule NADPH Oxidase 2 Inhibitor. Antioxid Redox Signal. 2015;23(5):358–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Bazil JN, Pannala VR, Dash RK, et al. Determining the origins of superoxide and hydrogen peroxide in the mammalian NADH:ubiquinone oxidoreductase. Free Radic Biol Med. 2014;77:121–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Pannala VR, Bazil JN, Camara AK, et al. A biophysically based mathematical model for the catalytic mechanism of glutathione reductase. Free Radic Biol Med. 2013;65:1385–1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Pannala VR, Bazil JN, Camara AK, et al. A mechanistic mathematical model for the catalytic action of glutathione peroxidase. Free Radic Res. 2014;48(4):487–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Pannala VR, Dash RK. Mechanistic characterization of the thioredoxin system in the removal of hydrogen peroxide. Free Radic Biol Med. 2015;78:42–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Harvey Motulsky AC. Fitting models to biological data using linear and nonlinear regression. New York (NY): Oxford University Press; 2004. [Google Scholar]


