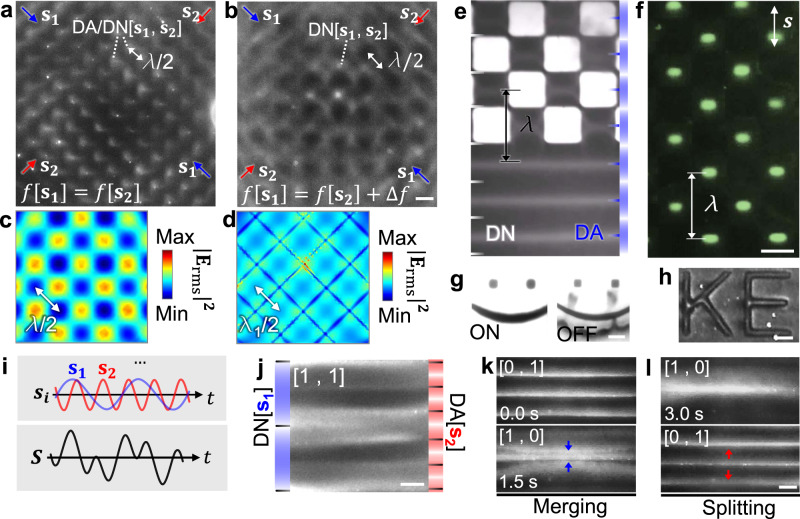
Fig. 4. Dynamic electric field control via wave superposition.

a Creating a 2D dot array of 100 nm polystyrene beads using orthogonal standing waves with identical frequencies (f[s₁] = f[s₂]). b The dot array pattern transforms to network with a mesh-like electric field distribution when f[s₁] ≠ f[s₂]. Numerically simulated magnitude of time-averaged electric field strength (${∣{\mathbf{E}}_{\mathrm{rms}}∣}^{\mathit{2}}$) for c f[s₁] = f[s₂] and d f[s₁] ≠ f[s₂]. e–h Forming complex 2D nanopatterns with 1D waves. Checkered patterns of e carbon nanotubes and f 100 nm polystyrene beads with selectively shielded checkered areas. Forming arbitrary 2D patterns of (g) carbon nanotubes and (h) 100 nm polystyrene beads using phase-sweeping acoustoelectronic waves and selective shielding. The carbon nanotubes can be released once the excitation is off. i Harmonic standing waves (s_i) with different tonal parameters are super-positioned to construct a complex electric field (S). When superimposing two harmonic waves (s₁ and s₂), the amplitudes are denoted as a vector Am(s₁, s₂) = a[m, n]. j Composite patterns of 100 nm polystyrene beads on both displacement nodes (DN) and antinodes (DA) when [m, n] is equal to [1, 1] (f (s₁) = 15.37 MHz, f (s₂) = 38.44 MHz). k Merging and l splitting of linear patterns of 100 nm beads using spatiotemporal control of harmonic acoustic waves. The labels “s” with arrow indicate the propagation directions of the standing waves. Scale bars: 60 μm. a and b, c and d, k and l share the same scale bars, respectively.