Abstract
目的
基于集成学习算法建立患者再入重症监护病房(intensive care unit, ICU)的风险预测模型，并比较各个模型的预测性能。
方法
使用美国重症医学数据库(medical information mart for intensive care，MIMIC)-Ⅲ，根据纳入、排除标准筛选患者，提取人口学特征、生命体征、实验室检查、合并症等可能对结局有预测作用的变量，基于集成学习方法随机森林、自适应提升算法(adaptive boosting, AdaBoost)和梯度提升决策树(gradient boosting decision tree, GBDT)建立再入ICU预测模型，并比较集成学习与Logistic回归的预测性能。使用五折交叉验证后的平均灵敏度、阳性预测值、阴性预测值、假阳性率、假阴性率、受试者工作特征曲线下面积(area under the receiver operating characteristic curve，AUROC)和Brier评分评价模型效果，基于最佳性能模型给出重要性排序前10位的预测变量。
结果
所有模型中，GBDT (AUROC=0.858)优于随机森林(AUROC=0.827)，略好于AdaBoost (AUROC=0.851)。与Logistic回归(AUROC=0.810)相比，集成学习算法在区分度上均有较大的提升。GBDT算法给出的变量重要性排序中，平均动脉压、收缩压、舒张压、心率、尿量、血肌酐等变量排序靠前，相对而言，再入ICU患者的心血管功能和肾功能更差。
结论
基于集成学习算法的患者再入ICU预测模型表现出较好的性能，优于Logistic回归。使用集成学习算法建立的再入ICU风险预测模型可用于识别再入ICU风险高的患者，医务人员可针对高风险患者采取干预措施，改善患者的整体临床结局。
Keywords: 重症监护病房, 病人再入院, 机器学习, 试验预期值
Abstract
Objective
To develop machine learning models for predicting intensive care unit (ICU) readmission using ensemble learning algorithms.
Methods
A publicly accessible American ICU database, medical information mart for intensive care (MIMIC)-Ⅲ as the data source was used, and the patients were selected by the inclusion and exclusion criteria. A set of variables that had the predictive ability of outcome including demographics, vital signs, laboratory tests, and comorbidities of patients were extracted from the dataset. We built the ICU readmission prediction models based on ensemble learning methods including random forest, adaptive boosting (AdaBoost), and gradient boosting decision tree (GBDT), and compared the prediction performance of the machine learning models with a conventional Logistic regression model. Five-fold cross validation was used to train and validate the prediction models. Average sensitivity, positive prediction value, negative prediction value, false positive rate, false negative rate, area under the receiver operating characteristic curve (AUROC) and Brier score were used as performance measures. After constructing the prediction models, top 10 predictive variables based on importance ranking were identified by the model with the best discrimination.
Results
Among these ICU readmission prediction models, GBDT (AUROC=0.858) had better performance than random forest (AUROC=0.827), and was slightly superior to AdaBoost (AUROC=0.851) in terms of AUROC. Compared with Logistic regression (AUROC=0.810), the discrimination of the three ensemble learning models was much better. The feature importance provided by GBDT showed that the top ranking variables included vital signs and laboratory tests. The patients with ICU readmission had higher mean arterial pressure, systolic blood pressure, diastolic blood pressure, and heart rate than the patients without ICU readmission. Meanwhile, the patients readmitted to ICU experienced lower urine output and higher serum creatinine. Overall, the patients having repeated admissions during their hospitalization showed worse heart function and renal function compared with the patients without ICU readmission.
Conclusion
The ensemble learning based ICU readmission prediction models had better performance than Logistic regression model. Such ensemble learning models have the potential to aid ICU physicians in identifying those patients with high risk of ICU readmission and thus help improve overall clinical outcomes.
Keywords: Intensive care units, Patient readmission, Machine learning, Predictive value of tests
重症监护病房(intensive care unit, ICU)的住院费用是国家医疗卫生预算中最高昂的花费之一，美国的一项研究显示，ICU中的住院花费占据了总体住院费用的13.4%[1]。住院期间，患者再入ICU的比例为4%~10%[2-3]，无计划的反复进入ICU的患者往往意味着更高的死亡风险、更长的住院时间和更高昂的花费。再入ICU的患者中，接近40%的患者由于原发基础疾病没有妥善解决导致病情反复而多次进入ICU[4-5]。因此，了解重症患者再入ICU的影响因素，建立重症患者再入ICU的风险预测模型可以了解患者是否有再入ICU的可能性，避免患者过早离开ICU而导致病情反复。
目前已建立的再入ICU预测模型大多基于Logistic回归[6]或使用ICU病情严重度评分[7]，预测性能有限。随着机器学习和人工智能技术的发展，在临床研究中使用更全面的方法建立预测模型，与ICU病情严重度评分相比可以得到更好的预测效果。Fialho等[8]使用模糊模型预测患者是否再入ICU，得到受试者工作特征曲线下面积(area under the receiver operating characteristic curve, AUROC)为0.720，高于ICU常用的急性生理和慢性健康评分(acute physiology and chronic health evaluation, APACHE)的预测效果。Desautels等[9]基于英国Addenbrooke医院的ICU患者数据，使用基于自适应提升算法(adaptive boosting, AdaBoost)的迁移学习预测患者再入ICU风险，模型的AUROC为0.710，高于病情严重度评分，即转运的稳定与负担指数评分(stability and workload index for transfer score，SWIFT)。以往文献中预测重症患者再入ICU模型的区分度较为一般，性能有待提高。
临床风险预测模型的建立往往基于结构化数据，集成学习是对结构化数据拟合效果最好的算法之一，随机森林、AdaBoost和梯度提升决策树(gra-dient boosting decision tree, GBDT)被广泛运用在Kaggle等数据科学竞赛中[10]，其中，GBDT具有参数设置简单、针对数据异常值性能亦较为稳健的特性，在临床建模中表现较为突出[11]，相对于其他机器学习方法，如神经网络、支持向量机、集成学习算法等，在结构化数据上表现较好，而且可以给出特征的重要性排序，计算花费也低于神经网络和支持向量机。本研究基于随机森林、AdaBoost、GBDT三种集成学习算法，建立重症患者再入ICU的风险预测模型，并将集成学习模型的预测效果与Logistic回归模型进行对比。
1. 资料与方法
1.1. 资料来源
数据来源于美国重症医学数据库(medical information mart for intensive care，MIMIC)-Ⅲ[12]，该数据库包含了2001—2012年Beth Israel Deaconess医疗中心ICU患者的个人数据和临床数据，数据中变量丰富，包含人口学特征、生命体征、实验室检查、手术情况、影像学检查和死亡情况等。
将住院期间进入ICU治疗的患者分成单次进入和重复进入两组，患者排除标准包括：(1)死亡患者，(2)新生儿ICU患者，(3)入住ICU时长小于24 h的患者，(4)年龄小于18或大于90岁的患者。
一次住院中患者有可能多次再入ICU，只选择第一次的再入ICU记录，确保每次住院只有一条记录纳入数据集。本研究筛选出的再入ICU记录为2 053条，未发生再入ICU的记录为33 656条。尽可能纳入较多的预测变量以获得更好的预测效果，所选择的进行预测建模的变量在原始数据集中的缺失率不高于20%。此外，对于单个患者缺失变量较多的情况，排除变量缺失率在30%以上的患者，最终用于建模的再入ICU记录为1 983条，未发生再入ICU的记录为32 179条。选择患者出ICU前最后24 h的记录作为模型的预测变量赋值。
1.2. 指标类型
1.2.1. 个体特征
包括年龄、性别、ICU入住时长、住院类型。
1.2.2. 生命体征
包括呼吸、心率、收缩压、舒张压、平均动脉压、血氧饱和度、体温、血糖。
1.2.3. 实验室检查
包括阴离子间隙、碳酸氢盐、肌酐、氯离子、血红蛋白、血细胞比容、血小板、钾离子、钠离子、血尿素氮、白细胞。
1.2.4. 格拉斯哥昏迷评分(Glasgow coma scale，GCS)
包括GCS总评分、GCS运动、GCS语言、GCS睁眼。
1.2.5. 合并症
包括Elixhauser合并症评分[13]中的所有合并症：心力衰竭、心律失常、瓣膜疾病、肺循环疾病、周围血管病、高血压、瘫痪、其他神经疾病、慢性肺病、没有合并症的糖尿病、有合并症的糖尿病、甲状腺功能减低、肾衰竭、肝病、溃疡、艾滋病、淋巴瘤、转移癌、未转移肿瘤、类风湿性关节炎、凝血病、肥胖、体质量下降、电解质紊乱、失血性贫血、缺铁性贫血、酒精滥用、药物滥用、精神病、抑郁。所有的合并症均通过MIMIC-Ⅲ数据库中的国际疾病分类(international classification of diseases, ICD)-9诊断编码来提取。
1.2.6. 其他指标
包括尿量、是否有气管插管等。
本研究纳入的变量同时重叠了APACHE评分[7]和SWIFT评分[14]中大部分指标，因患者的生命体征在24 h内经多次测量，为反映患者生命体征在24 h内的变化情况，生命体征的最大值、最小值也作为预测模型的输入变量入选，本研究总计纳入67个变量。
1.3. 数据预处理
MIMIC-Ⅲ作为真实世界的数据库，同样存在数据缺失情况，有相关研究比较了均值填补法和线性插值法处理缺失值的效果，发现线性插值法对数据缺失值的拟合效果更好[15]，因此，本研究也根据线性插值法填补缺失值。在ICU住院患者中，发生再入ICU的只占总数据的5.7%，发生再入ICU和未发生再入ICU的数据比例极为不平衡。在未发生再入ICU的样本占绝大多数的情况下，分类器将所有样本预测为多数类样本，也可以得到很高的准确率，但这样的预测就失去了意义。大多数标准的机器学习算法是针对平衡数据设计的算法，过度不平衡的数据会严重影响算法的预测能力。目前解决数据不平衡的方法主要有采样、数据合成和加权等方法，本文采用两种采样方法处理不平衡数据，即随机下采样和NearMiss方法[16]。随机采样是在多数类样本中随机选择一部分样本，使多数类和少数类样本数量平衡。NearMiss方法主要是基于K近邻(K-nearest neighbor)的思想来达到下采样的目的。NearMiss是寻找每个多数类样本最近的3个少数类样本，计算其平均距离，选择平均距离最小的多数类样本组成新的样本子集。本研究将原始数据集分成80%的训练集和20%的测试集，用于评估经过随机下采样方法和NearMiss方法处理后的数据对模型性能的影响。使用预处理后的数据训练预测模型，根据模型在测试集上的准确率来评估不平衡数据处理方法的优劣。从随机下采样和NearMiss方法的准确率可以看出，NearMiss方法可以较大程度地提升分类器的性能(表 1)。因此，本研究使用NearMiss方法来处理不平衡数据，再进行建模预测。
表 1.
随机下采样和NearMiss方法处理不平衡数据的性能
Performance comparison between random under-sampling and NearMiss methods
| Classifier | Accuracy | |
| Random under-sampling | NearMiss | |
| AdaBoost, adaptive boosting; GBDT, gradient boosting decision tree. | ||
| Logistic regression | 0.615 | 0.838 |
| Random forest | 0.542 | 0.844 |
| AdaBoost | 0.620 | 0.873 |
| GBDT | 0.626 | 0.874 |
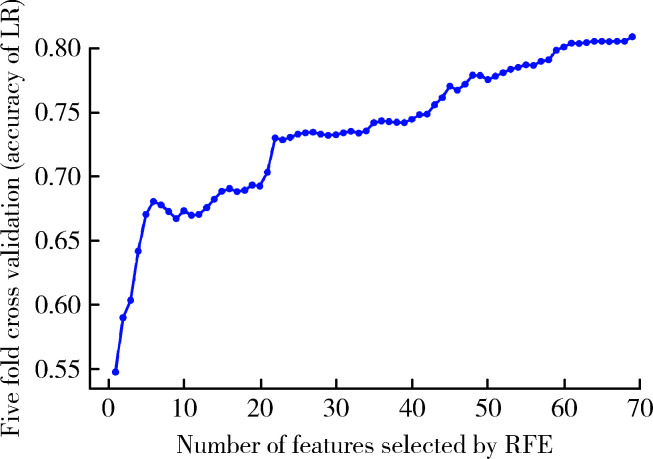
在建模之前，本研究进行了特征选择，使用基于Logistic回归的递归特征消除法寻找最佳的预测变量的组合。递归特征消除结果显示，在特征不断增加的同时，模型的预测性能也在不断上升(图 1)。因此，基于Logistic回归的递归特征消除法提示本研究纳入的所有特征均对模型的预测效果有贡献，如果只选取部分特征，可能导致模型预测性能的下降，故本研究纳入所有特征，不对特征进行选择，以确保最佳的预测性能。
图 1.
基于Logistic回归的递归特征消除法
Recursive feature elimination based on Logistic regression
RFE, recursive feature elimination; LR, Logistic regression.
1.4. 预测模型
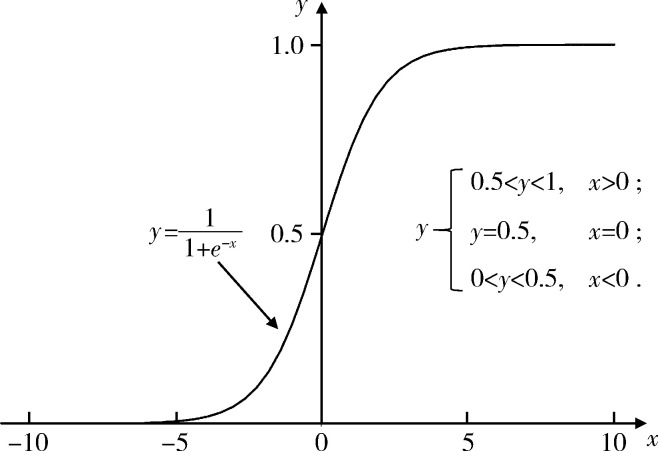
Logistic回归中因变量是二分类变量，无需事先假设数据分布，将样本落入某一类的后验概率建模为Logit函数(图 2)。使用Logit函数可以将自变量的线性组合转化为0~1之间的预测值，得到发生某一类别事件的概率，并根据概率大小来判定结局的类别，因可解释性强而使用广泛。
图 2.
Logit函数示意图
Logit function
随机森林[17]主要使用装袋法(bagging)的并行式方法进行集成学习，以决策树为基础分类器，Logistic回归模型中的自变量x对应于决策树模型中的节点特征变量，因变量y值对应于决策树中的叶节点变量值(图 3)。在随机森林的训练过程中，首先通过bootstrap方法，从N个训练样本数据集中随机有放回抽样N次，其中部分样本会重复，在N次抽样中样本始终不被抽到的比例为
，N取极限时，总体样本中约有36.8%的样本不会出现在采样集中。总共抽取T个采样集，每个采样集的样本组成各不相同，此外，随机森林的随机性还体现在随机特征选择。使用采样集训练基础分类器的过程中，从总体特征随机选择包含k个特征的子集，再从子集中选择基尼不纯度(Gini impurity)最小的特征并确定当前的决策树节点。每个采样集训练出一个基础分类器就组成最终的随机森林模型，利用该模型进行分类决策时，T个基础分类器投票决定分类结果。
图 3.
决策树示意图
Decision tree
a, b, c, d, represent the threshold of feature value in node splitting.
AdaBoost[18]是集成学习提升法(boosting)的代表算法，使用基础分类器单层决策树进行串行训练而获得更强的分类器。每一轮训练，根据当前基础分类器的误差率em(m为迭代次数，m=1，2，…，M)来确定本轮基础分类器权重am，同时更新样本权重，并根据新的样本权重训练下一个基础分类器Gm+1(x)，最终AdaBoost的输出是所有基础分类器的加权组合。
首先计算基础分类器在训练集上的分类误差率：
 |
1 |
其中，N为样本总数，wmi是第m轮迭代中第i个样本的权重，I代表结果为0或1的指示函数，在训练第一个基础分类器G1时，为N个训练样本分配相等的权重。分类器的误差率越大，其在最终模型中所占的比重就越小，根据分类器的误差率确定每个分类器的权重am：
 |
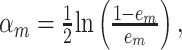2 |
同时，更新训练样本的权重，为分类错误的样本分配更高的权重：
 |
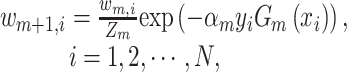3 |
其中，Zm为规范化因子，计算公式为：
 |
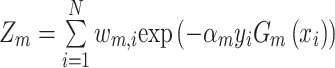4 |
接下来进行下一个基础分类器Gm+1(x)(m+1≤M)的训练，每次迭代中生成新的基础分类器可以最佳地拟合当前加权样本。AdaBoost的输出是各基础分类器结果的加权组合，公式为：
 |
5 |
对f(x)输出的概率进行判别，得到最终的分类结果。
GBDT[19]是改进的提升法(boosting)算法，以分类和回归树(classification and regression tree, CART)作为基础分类器，将一系列CART串联起来得到集成学习模型。开始训练时，所有的样本x有相同的初始化F0(x)，在m(m=2，3，…，M)次迭代的过程中，计算模型预测值Fm-1(x)与真实值的残差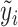
，再建立CART拟合模型的残差，最后组合Fm-1(x)与CART的输出得到新一轮的预测模型Fm(x)，其中，模型预测值与真实值的残差
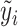是通过损失函数相对于Fm-1(x)的负梯度近似得到。GBDT每一次迭代，拟合的误差都会减小。本研究的主要预测结局为二分类变量，GBDT用于二分类问题的损失函数定义为：
 |
6 |
其中，F(x)为：
 |
7 |
GBDT模型的最终目标是找到使损失函数(7)最小的F(x)，进而计算样本的预测概率，得到样本分类的结果。建立二分类的GBDT模型，首先根据公式(8)初始化GBDT模型：
 |
8 |
在接下来的GBDT模型迭代过程中，为了让每次迭代的损失函数最小，每次迭代时要往损失函数的负梯度方向移动，第m(m=2，…，M)次迭代的负梯度
即为前一次迭代中模型的预测值Fm-1(x)与真实值yi残差的近似：
 |
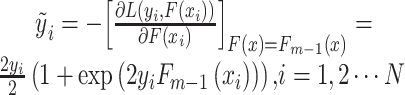9 |
随后用样本数据{xi}和公式(10)计算得到的负梯度值
形成新的训练数据集{xi, 
}1N(N为样本数量)，训练出具有J个终止节点(叶子节点)的CART模型{Rjm}1J，进一步计算CART叶子节点的值：
 |
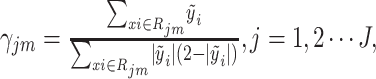10 |
获得新的基础分类器的输出后，将CART的输出结果与上一轮模型Fm-1(x)串联后就可以得到GBDT的当前模型Fm(x)：
 |
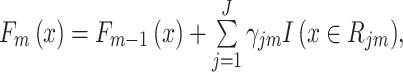11 |
最终模型预测概率值为：
 |
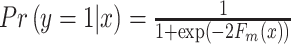12 |
1.5. 建立模型
使用PostgreSQL在MIMIC-Ⅲ数据库中进行数据筛选，描述研究人群的基本特征，根据数据分布选择卡方检验或秩和检验比较组间差异。基于Logistic回归、随机森林、AdaBoost和GBDT四种方法预测建模，使用五折交叉验证来训练和验证模型的判别能力。基于灵敏度、阳性预测值、阴性预测值、假阳性率、假阴性率、AUROC、Brier评分来评价模型的预测能力，其中，前5项是临床建模较为常用的指标，Brier评分衡量了模型总体概率预测的准确性，AUROC衡量了模型总体判别患者是否再入ICU的区分度。在建立预测模型的同时，利用预测效果最好的模型给出重要性排序前10位的预测变量，变量的全局重要性通过五折交叉验证的重要性均值得到。使用R 3.5.1和Python 3.6软件进行分析。
2. 结果
2.1. 数据基本情况
本研究纳入ICU住院记录34 162条，其中发生再入ICU的住院记录1 983条，患者在住院期间再入ICU率为5.7%，仅使用无缺失值的数据进行描述性统计分析。与未发生再入ICU的患者相比，发生再入ICU的患者平均年龄更大，ICU住院时间更长，GCS的总分和各项GCS评分更低，因非择期手术而入院的患者比例更高(表 2)。
表 2.
有无再入ICU的重症患者基本情况比较
The characteristics of critically ill patients with and without ICU readmission
| Characteristics | Total | Patients with ICU readmission | Patients without ICU readmission | P value |
| a, χ2 test; b, Wilcoxon Rank-Sum test. ICU, intensive care unit; GCS, Glasgow coma scale. | ||||
| Ageb/years, x±s | 62.67±16.22 | 64.08±15.16 | 62.58±16.29 | < 0.001 |
| Gender (female)a, n (%) | 11 319 (42.38) | 671 (41.69) | 10 648 (42.49) | 0.16 |
| ICU stayb/d, x±s | 4.56±5.60 | 5.46±6.12 | 4.50±5.56 | < 0.001 |
| GCS total scoreb, x±s | 14.33±1.42 | 14.17±1.58 | 14.34±1.41 | < 0.001 |
| GCS motorb, x±s | 5.89±0.50 | 5.88±0.50 | 5.89±0.50 | 0.08 |
| GCS verbalb, x±s | 4.41±1.28 | 4.40±1.18 | 4.41±1.29 | < 0.001 |
| GCS eyesb, x±s | 3.75±0.54 | 3.73±0.56 | 3.75±0.54 | 0.10 |
| Admission typea, n (%) | ||||
| Medical | 18 208 (68.17) | 1 054 (63.92) | 17 154 (68.45) | |
| Scheduled surgery | 3 620 (13.55) | 179 (10.86) | 3 441 (13.73) | < 0.001 |
| Unscheduled surgery | 4 881 (18.27) | 416 (25.23) | 4 465 (17.82) | |
2.2. 预测模型性能
基于Logistic回归、随机森林、AdaBoost和GBDT算法建立预测模型，4个模型的五折交叉验证后的结果见表 3，其中，GBDT的区分度最好，平均AUROC达到0.858，AdaBoost (AUROC=0.851)的区分度略差于GBDT，随机森林(AUROC=0.827)的预测效果第三，Logistic回归(AUROC=0.810)的预测效果最差。
表 3.
Logistic回归、随机森林、AdaBoost和GBDT模型预测再入ICU的性能
The prediction performance of Logistic regression, random forest, AdaBoost, and GBDT
| Performance | Logistic regression | Random forest | AdaBoost | GBDT |
| AdaBoost, adaptive boosting; GBDT, gradient boosting decision tree; ICU, intensive care unit; PPV, positive predictive value; NPV, negative predictive value; FPR, false positive rate; FNR, false negative rate; AUROC, area under the receiver operating characteristic curve. Data are presented as x±s. | ||||
| Sensitivity | 0.763±0.029 | 0.787±0.010 | 0.821±0.029 | 0.817±0.028 |
| PPV | 0.843±0.022 | 0.858±0.056 | 0.876±0.040 | 0.892±0.038 |
| NPV | 0.784±0.018 | 0.802±0.012 | 0.832±0.020 | 0.832±0.017 |
| FPR | 0.143±0.026 | 0.134±0.057 | 0.120±0.044 | 0.101±0.040 |
| FNR | 0.237±0.029 | 0.213±0.010 | 0.179±0.029 | 0.183±0.028 |
| AUROC | 0.810±0.013 | 0.827±0.029 | 0.851±0.017 | 0.858±0.013 |
| Brier score | 0.190±0.013 | 0.173±0.029 | 0.149±0.017 | 0.142±0.013 |
从预测模型的灵敏度、阳性预测值、阴性预测值、假阳性率、假阴性率和Brier评分的结果可以看出，GBDT的灵敏度略差于AdaBoost，阴性预测值与AdaBoost相当，阳性预测值、假阳性率、假阴性率和Brier评分的表现都是4个模型中最好的。在集成学习模型的总体预测效果中，GBDT的预测效果优于随机森林，略好于AdaBoost。对比集成学习和Logistic回归的预测效果，集成学习算法与Logistic回归相比均有较大的提升，能够提供更为精确的再入ICU风险预测。
再入ICU的预测模型中，预测性能最佳的GBDT算法给出的预测变量的重要性排序见表 4，排序靠前的变量为血小板、血糖、尿量、血压、心率和血肌酐等，以实验室检查和生命体征变量为主。由表 4可见，心血管功能方面，发生再入ICU患者的平均动脉压、收缩压、舒张压和心率比未发生再入ICU的患者更高；肾功能方面，再入ICU的患者尿量更少、血肌酐更高。总体来说，再入ICU的患者心血管功能和肾功能比未发生再入ICU的患者更差。
表 4.
基于GBDT模型重要性排序前10位的变量及分布
Top 10 variables identified by feature importance based on GBDT model and their distributions
| Rank | Variables | Importance | With ICU readmission, x±s | Without ICU readmission, x±s |
| Abbreviations as in Table 3. | ||||
| 1 | Platelet/(×103/μL) | 0.109 | 240.05±154.37 | 230.05±131.88 |
| 2 | Glucose (maximum)/(mg/dL) | 0.093 | 208.36±109.04 | 199.68±104.80 |
| 3 | Urine output/mL | 0.089 | 1 908.70±1 111.36 | 2 089.51±1 129.90 |
| 4 | Mean arterial pressure (maximum)/mmHg | 0.067 | 122.04±43.03 | 116.87±38.68 |
| 5 | Glucose (minimum)/(mg/dL) | 0.058 | 96.06±33.03 | 99.83±35.78 |
| 6 | Heart rate (maximum)/(beat/min) | 0.058 | 114.38±25.07 | 109.35±23.49 |
| 7 | Creatinine/(mg/dL) | 0.053 | 1.33±1.24 | 1.19±1.23 |
| 8 | Systolic blood pressure (maximum)/mmHg | 0.042 | 160.42±29.69 | 158.04±28.14 |
| 9 | Diastolic blood pressure (minimum)/mmHg | 0.035 | 40.47±12.59 | 41.99±12.85 |
| 10 | Heart rate (minimum)/(beat/min) | 0.031 | 68.79±15.12 | 68.30±14.46 |
3. 讨论
本研究使用美国MIMIC-Ⅲ数据库，基于集成学习算法建立重症患者再入ICU的风险预测模型，其中，GBDT算法预测效果最好，平均AUROC达到0.858，高于随机森林(AUROC=0.827)、AdaBoost (AUROC=0.851)和Logistic回归(AUROC=0.810)。
集成学习算法是目前对结构化数据拟合效果最好的算法之一，本研究主要基于集成学习算法建立患者再入ICU的风险预测模型，对比了多种模型的预测效果，与生物医学领域运用广泛的Logistic回归相比，集成学习模型具有更好的预测性能。与已报道的再入ICU风险预测模型相比，本研究中预测模型的区分度更高，能够更好地预测患者再入ICU风险。早期识别高风险的患者，有助于临床医生进行更好的医疗决策。
本研究采用了两种数据平衡算法进行数据预处理，与随机下采样相比，NearMiss方法较好地提升了模型的性能。随机下采样在处理样本的过程中，丢失了大量多数类样本的信息，存在样本代表性不足的问题。NearMiss方法通过K近邻算法，选择了离少数类样本距离最近的多数类样本，较好地保留了原始样本的决策边界[20]，因此比随机下采样的样本代表性更好，对模型的提升更为显著。
医学领域预测患者再入ICU的研究中，一般采用ICU中常用的疾病严重程度评分(如APACHE评分和SWIFT评分)来评估患者再入ICU的风险[7, 14]。APACHE的评分项目中包含了生命体征和实验室检查等生理指标，年龄、入院类型等个体特征，GCS评分，肝脏、心血管、肺部疾病等合并症；SWIFT评分包括患者入院类型，ICU住院时长，还有部分生理指标(PaCO2和FiO2)。本研究纳入的变量同时重叠了APACHE评分和SWIFT评分中的大部分指标，尽可能全面地反映患者疾病的严重程度。GBDT的再入ICU风险预测模型中，重要性排序靠前的变量包括了血小板、血糖、尿量、血压、心率和血肌酐，实验室检查和生命体征的相关变量排序靠前。Fialho等[8]基于MIMIC-Ⅱ数据中的生理学指标预测患者再入ICU风险，选出了最具有预测作用的6个变量，分别为心率、体温、血小板、血压、氧分压和乳酸。患者在ICU出院前24 h的血小板、血压和心率在不同研究中都具有较强的预测作用，表明在临床工作中可以对ICU患者的这些指标进行常规监测，及时发现并干预指标表现较差的患者。Fialho等[8]的预测模型包含的变量只有实验室检查和生命体征指标，本研究纳入了更为丰富的预测变量，涵盖了人口统计学指标、合并症、GCS评分、实验室检查和生命体征等多个维度的信息，更能全面反映患者疾病的状况，且MIMIC-Ⅲ数据库记录有横跨10年的患者样本，相对而言提升了本文模型的代表性。
本研究也存在一定的不足之处，集成学习模型虽然预测效果更好，但对变量特征的解释性不强，Logistic回归尽管有较好的可解释性，然而模型性能表现不佳。未来研究应注重于开发预测能力高、可解释性好的模型，在提供临床决策支持方面更易于医生理解和接受。
总体而言，基于集成学习算法的再入ICU风险预测模型能够较好地辅助医生识别再入ICU风险高的患者，对这部分患者采取干预措施，可以预防可能发生的再入ICU，提高ICU救治的医疗质量，改善患者的预后，同时也节省了大量的医保费用。
Funding Statement
国家自然科学基金(81771938、91846101)、北京市自然科学基金(7212201)、北京大学医学部-密歇根大学医学院转化医学与临床研究联合研究所项目(BMU2020JI011)
Supported by the National Natural Science Foundation of China (81771938, 91846101), the Beijing Municipal Natural Science Foundation (7212201), the Project of the University of Michigan Health System-Peking University Health Science Center Joint Institute for Translational and Clinical Research (BMU2020JI011)
References
- 1.Halpern NA, Pastores SM. Critical care medicine in the United States 2000-2005: an analysis of bed numbers, occupancy rates, payer mix, and costs. Crit Care Med. 2010;38(1):65–71. doi: 10.1097/CCM.0b013e3181b090d0. [DOI] [PubMed] [Google Scholar]
- 2.Woldhek AL, Rijkenberg S, Bosman RJ, et al. Readmission of ICU patients: A quality indicator? J Crit Care. 2017;38:328–334. doi: 10.1016/j.jcrc.2016.12.001. [DOI] [PubMed] [Google Scholar]
- 3.Kramer AA, Higgins TL, Zimmerman JE. The association between ICU readmission rate and patient outcomes. Crit Care Med. 2013;41(1):24–33. doi: 10.1097/CCM.0b013e3182657b8a. [DOI] [PubMed] [Google Scholar]
- 4.Rosenberg AL, Hofer TP, Hayward RA, et al. Who bounces back? Physiologic and other predictors of intensive care unit readmission. Crit Care Med. 2001;29(3):511–518. doi: 10.1097/00003246-200103000-00008. [DOI] [PubMed] [Google Scholar]
- 5.Baker DR, Pronovost PJ, Morlock LL, et al. Patient flow variabi-lity and unplanned readmissions to an intensive care unit. Crit Care Med. 2009;37(11):2882–2887. doi: 10.1097/CCM.0b013e3181b01caf. [DOI] [PubMed] [Google Scholar]
- 6.Martin LA, Kilpatrick JA, Al-Dulaimi R, et al. Predicting ICU readmission among surgical ICU patients: Development and validation of a clinical nomogram. Surgery. 2019;165(2):373–380. doi: 10.1016/j.surg.2018.06.053. [DOI] [PubMed] [Google Scholar]
- 7.Lee H, Lim CW, Hong HP, et al. Efficacy of the APACHE Ⅱ score at ICU discharge in predicting post-ICU mortality and ICU readmission in critically ill surgical patients. Anaesth Intensive Care. 2015;43(2):175–186. doi: 10.1177/0310057X1504300206. [DOI] [PubMed] [Google Scholar]
- 8.Fialho AS, Cismondi F, Vieira SM, et al. Data mining using clinical physiology at discharge to predict ICU readmissions. Expert Syst Appl. 2012;39(18):13158–13165. doi: 10.1016/j.eswa.2012.05.086. [DOI] [Google Scholar]
- 9.Desautels T, Das R, Calvert J, et al. Prediction of early unplanned intensive care unit readmission in a UK tertiary care hospital: a cross-sectional machine learning approach. BMJ Open. 2017;7(9):e017199. doi: 10.1136/bmjopen-2017-017199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hosni M, Abnane I, Idri A, et al. Reviewing ensemble classification methods in breast cancer. Comput Methods Programs Biomed. 2019;177:89–112. doi: 10.1016/j.cmpb.2019.05.019. [DOI] [PubMed] [Google Scholar]
- 11.Liu Y, Gu Y, Nguyen JC, et al. Symptom severity classification with gradient tree boosting. J Biomed Inform. 2017;75:S105–S111. doi: 10.1016/j.jbi.2017.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Johnson AE, Pollard TJ, Shen L, et al. MIMIC-Ⅲ, a freely accessible critical care database. Sci Data. 2016;3:160035. doi: 10.1038/sdata.2016.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Austin SR, Wong YN, Uzzo RG, et al. Why summary comorbidity measures such as the Charlson comorbidity index and Elixhauser score work. Med Care. 2015;53(9):E65–E72. doi: 10.1097/MLR.0b013e318297429c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Oakes DF, Borges IN, Forgiarini Junior LA, et al. Assessment of ICU readmission risk with the stability and workload index for transfer score. J Bras Pneumol. 2014;40(1):73–76. doi: 10.1590/S1806-37132014000100011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xue Y, Klabjan D, Luo Y. Predicting ICU readmission using grouped physiological and medication trends. Artif Intell Med. 2019;95:27–37. doi: 10.1016/j.artmed.2018.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.He HB, Garcia EA. Learning from imbalanced data. IEEE T Knowl Data En. 2009;21(9):1263–1284. doi: 10.1109/TKDE.2008.239. [DOI] [Google Scholar]
- 17.Rahman R, Matlock K, Ghosh S, et al. Heterogeneity aware random forest for drug sensitivity prediction. Sci Rep. 2017;7(1):11347. doi: 10.1038/s41598-017-11665-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hu J. Automated detection of driver fatigue based on AdaBoost classifier with EEG signals. Front Comput Neurosci. 2017;11:72. doi: 10.3389/fncom.2017.00072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Friedman JH. Greedy function approximation: A gradient boosting machine. Ann Stat. 2001;29(5):1189–1232. doi: 10.1214/aos/1013203450. [DOI] [Google Scholar]
- 20.Mani I, Zhang I. kNN approach to unbalanced data distributions: a case study involving information extraction[C]// ICML 2003 Workshop on Learning from Imbalanced Datasets, August 21-24, 2003. Washington, D.C. : ICML, 2003.