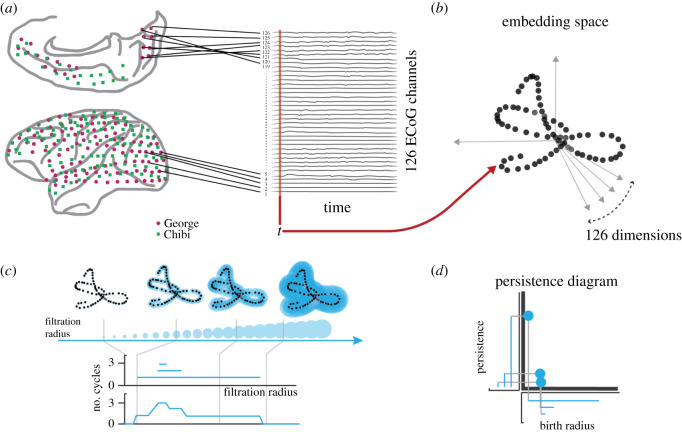
Figure 2.

Construction of the embedded point cloud from a multidimensional time series. Every time-step in the recording corresponds to a single column vector in a C × T array (a), and this vector can be imagined as a point in a C-dimensional space, creating a point-cloud that traces out the trajectory of the system through this space as it evolves (b). We then computed the persistent homology of the complex defined by these points using cosine distance recording the evolution of connected components and cycles throughout the filtration. The process can be thought of as spheres centred on each embedded point with growing radius. As the radius of the spheres grow and begin to overlap, a discretized approximation of the underlying manifold emerges. To classify the evolving manifold, we use two summaries: the Betti curve, that counts the number of cycles present in the discretized manifold for each filtration radius (c); and the persistence diagram, that encodes each cycle as a point and records the radius of its first appearance (birth radius) in the x-axis and until which radius it persists in the y-axis (d).