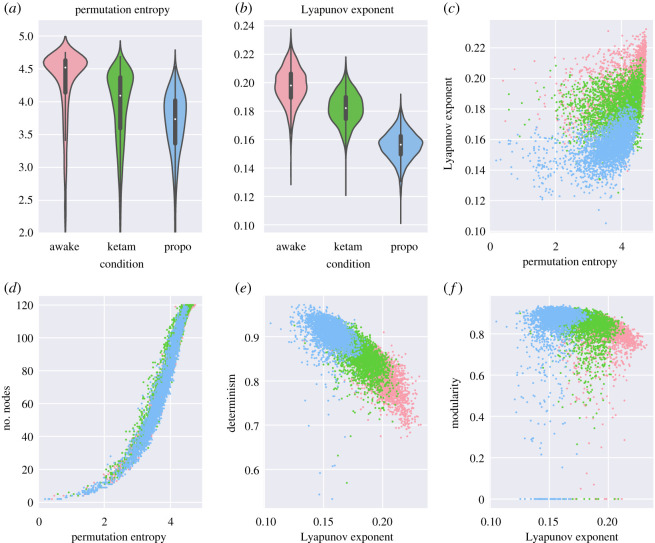
Figure 6.

(a,b) Violin plots of the permutation entropy and the Lyapunov exponent. As with the OPN measures, we chose violin plots to capture the distribution of a large number of channels. (c) A scatter plot of the permutation entropy against the Lyapunov exponent: note the positive, but nonlinear relationship between both measures, consistent with previous work showing an association between permutation entropy and chaos [48]. (d–f) Scatter plots showing how the two time-series measures relate to the OPN measures. The scatter-plots show that these novel measures derived from the OPN are consistent with established measures. As expected, the number of nodes is positively associated with the permutation entropy (d). The Lyapunov exponent is negatively correlated with the determinism (which is consistent with the results reported in [70] and consistent with the intuition behind chaotic systems) (e). Finally, there is a slight negative relationship between the Lyapunov exponent and the modularity, suggesting that metastable higher-order dynamics may be harder to maintain in chaotic systems (f).