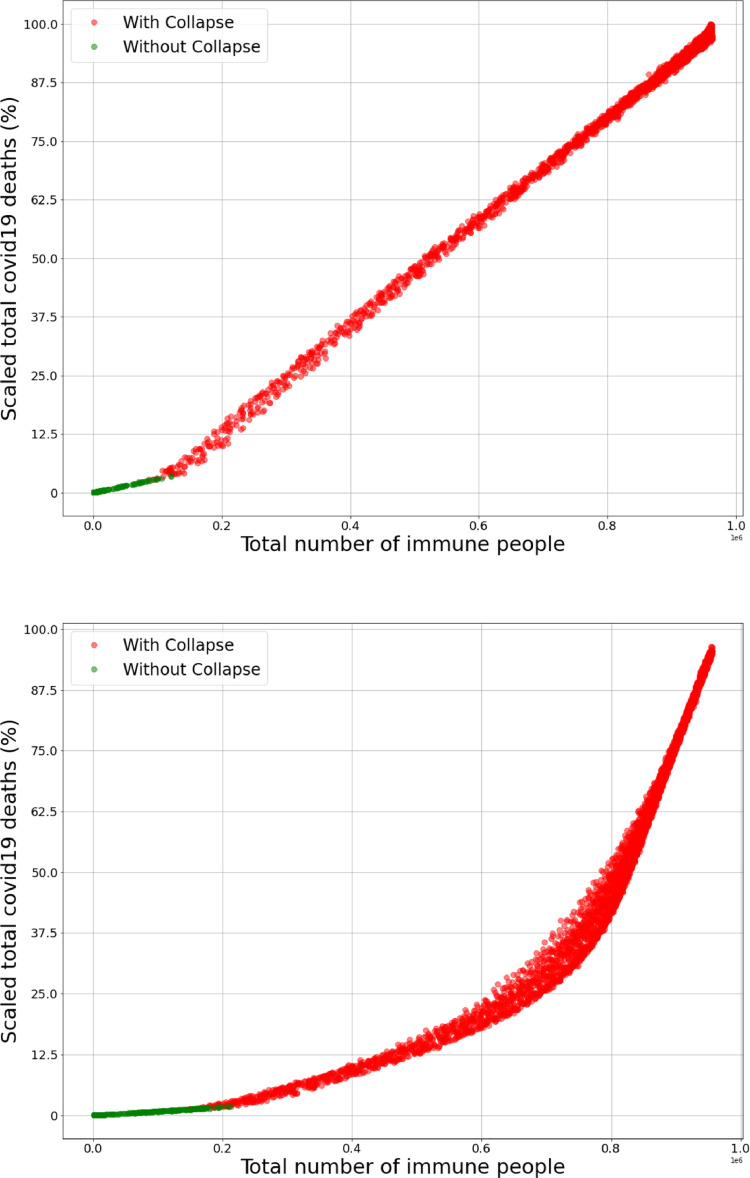
Fig. 11.

Total number of immune people vs. total COVID-19 deaths (scaled in percentage with the maximum number of deaths obtained in the simulations). Both graphs present an increasing functional dependence between the two variables; (a) presents data from basic behavioural scenarios; the data from scenarios with functioning healthcare system (without collapse) and scenarios in collapse lie on two different linear functions with a discontinuity of the first kind in the first derivative which is an emblematic representation of the healthcare system collapse (individuals which could be saved start to die). (b) presents data from special groups behavioural scenarios; the data from scenarios with functioning healthcare system (without collapse) lie on an even less deadly linear function compared to the one in (a) (the slope of the line is smaller). Notice that $f\left(x\right)<g\left(x\right)$ for every $x$, where $f$ represents the function in (a) and $g$ in (b) reconfirming that the special groups behavioural scenario is expected to be significantly less deadly in every possible scenario. It is interesting to notice that $g$ is not linear and a smoothing effect is present, also around $x=70\%$ the slope of the mortality increases rapidly (due to the fact that a large portion of risky clusters becomes infected).