Figure 5.

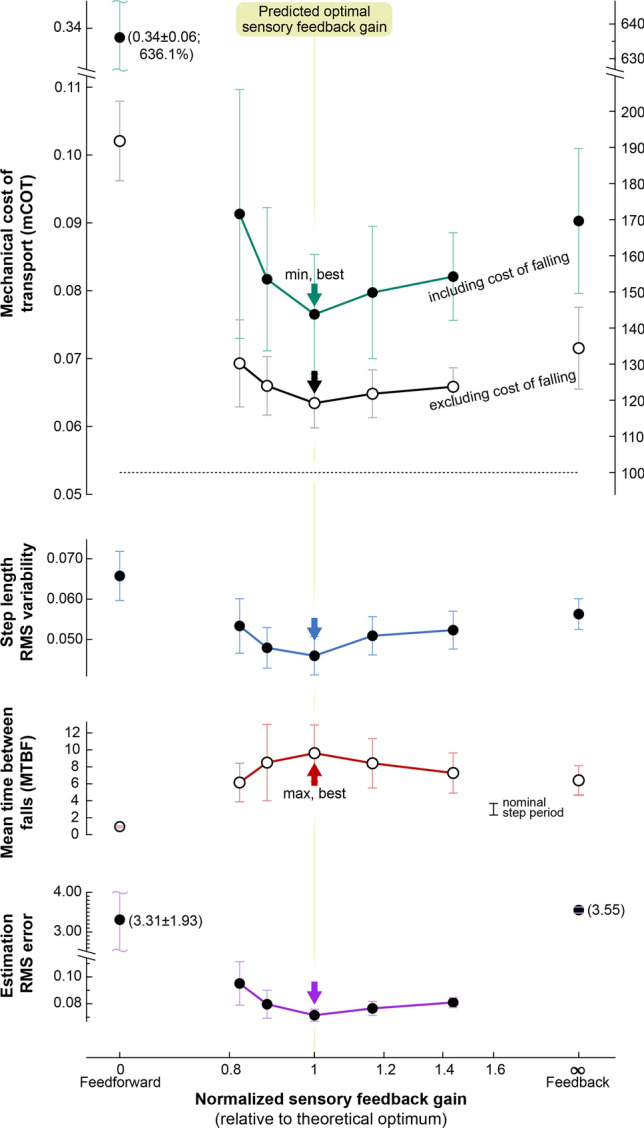
State estimation accuracy and walking performance under noisy conditions, as a function of sensory feedback gain. The theoretically optimal sensory feedback gain (normalized gain of 1) yielded best performance, in terms of mechanical cost of transport (mCOT), step length variability, mean time between falls (MBTF), and state estimator error. Normalized sensory feedback gain varies between extremes of pure feedforward (to the left) and pure feedback (to the right), with 1 corresponding to theoretically predicted optimum $L_{\text{lqe}}^{\ast }$. Formally, normalized gain is defined as $\left|L\right|/\left|L_{\text{lqe}}^{\ast }\right|,$ where $\left|·\right|$ denotes matrix norm. Vertical arrow indicates best performance (minimum for all measures except maximum for MTBF). For all gains, model was simulated with a fixed combination of process and sensor noise as input to multiple trials, yielding ensemble average measures. Each data point is an average of 20 trials of 100 steps each, and errorbar indicates standard deviation of the trials. Mechanical cost of transport (mCOT) was defined as positive work divided by body weight and distance travelled, and step variability as root-mean-square (RMS) variability of step length. Falling takes time and dissipates mechanical energy, and so mCOT was computed both including and excluding losses from falls (work, time, distance).