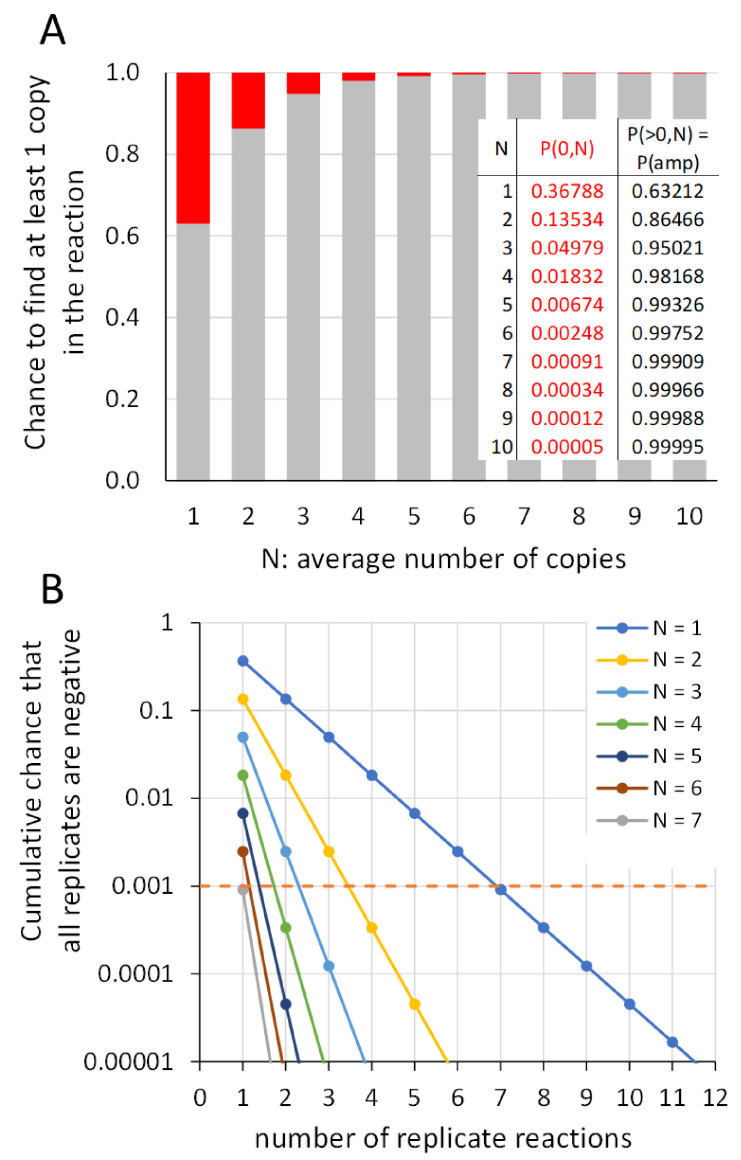
Figure 9.

Number of technical replicates needed to declare that a sample is negative. (A) Bar graph of the chance, governed by the Poisson distribution, that a PCR reaction contains a target copy and thus shows amplification (grey; P(amp)) or not (red; P(0,N)) for the average number of targets per reaction volume ranging from one to ten. When no amplification is observed, the reaction is a false negative (P(FN)). (B) Cumulative P(FN) for a number of technical replicates for different inputs in the reaction (colored lines). The graph shows that in the worst-case situation, i.e., an average input of only one target copy per reaction (blue line), seven negative replicate reactions are needed for the researcher to be 99.9% sure (dashed pink line) that the sample is indeed negative. Note that only one positive replicate is needed to decide that the sample is positive. For samples with on average seven, or more, copies per reaction volume, the chance that a single reaction is positive is already 99.9% or higher.