Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis

Jalal Poorolajal; Shahla Noornejad

doi:10.1371/journal.pone.0253341

. 2021 Jun 28;16(6):e0253341. doi: 10.1371/journal.pone.0253341

Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis

Jalal Poorolajal ^1,^2,^*, Shahla Noornejad ³

Editor: Mohammad Asghari Jafarabadi⁴

PMCID: PMC8238175 PMID: 34181682

Abstract

Background

The proposed sequential and combinatorial algorithm, suggested as a standard tool for assessing, exploring, and reporting heterogeneity in the meta-analysis, is useful but time-consuming particularly when the number of included studies is large. Metaplot is a novel graphical approach that facilitates performing sensitivity analysis to distinguish the source of substantial heterogeneity across studies with ease and speed.

Method

Metaplot is a Stata module based on Stata’s commands, known informally as "ado". Metaplot presents a two-way (x, y) plot in which the x-axis represents the study codes and the y-axis represents the values of I² statistics excluding one study at a time (n-1 studies). Metaplot also produces a table in the ’Results window’ of the Stata software including details such as I² and χ² statistics and their P-values omitting one study in each turn.

Results

Metaplot allows rapid identification of studies that have a disproportionate impact on heterogeneity across studies, and communicates to what extent omission of that study may reduce the overall heterogeneity based on the I² and χ² statistics. Metaplot has no limitations regarding the number of studies or types of outcome data (binomial or continuous data).

Conclusions

Metaplot is a simple graphical approach that gives a quick and easy identification of the studies having substantial influences on overall heterogeneity at a glance.

Introduction

The studies that are brought together in a meta-analysis inevitably differ in many aspects. This variability across studies is called heterogeneity [1]. The between-studies heterogeneity can be assessed by the chi-square test also written as χ² or Chi² and can be quantified by I² statistics [2, 3]. When there is heterogeneity in a meta-analysis, the source of heterogeneity across studies should be carefully investigated on a case-by-case basis [4].

A common approach, which was proposed by Patsopoulos et al, is to perform a sensitivity analysis based on a sequential and combinatorial algorithm [5]. According to this algorithm, one study is excluded from the meta-analysis at a time and the impact of the excluded study on the between-study heterogeneity is evaluated based on I² statistic and χ² test. This ‘one-out’ sensitivity analysis tells us to what extent the overall heterogeneity changes by excluding a particular study at a time. Then, the study that is responsible for the largest decrease in I² value should be dropped out. This process is repeated for a new set of n-1 studies. This sequential and combinatorial algorithm is repeated several times until the I² statistic drops below the desired threshold value of 50%. In the last step, there is a possibility that more than one omitted study can result in I² dropping below the intended threshold. In such cases, the algorithm that results in the maximum decrease in the I² statistic below the desired threshold is selected. There is a chance that two or more studies cause the same reduction in I² by their exclusion. In this case, the study with the largest reduction in χ² statistic (the least χ² statistic) is dropped out.

Based on the aforementioned algorithm, this ‘one-out’ sensitivity analysis must be repeated n-1 times to specify and exclude the outlying study from the meta-analysis. If the desired threshold value of 50% is not achieved in the first step, the algorithm must be repeated n-2, n-3, etc. Therefore, this algorithm may be boring and time-consuming when the number of included studies is large and the between-studies heterogeneity is substantial.

In this study, we aimed to introduce a novel Stata graph that performs the ‘one-out’ sensitivity analysis for n-1 studies and identifies immediately the studies responsible for substantial heterogeneity across studies by executing "metaplot.ado" Stata command.

Methods

Metaplot is a Stata module based on Stata’s commands, known as "ado". Metaplot produces a two-dimensional (x, y) Stata graph. The x-axis represents the included studies. The studies are shown on this axis by an ID code. The y-axis represents the values of I² statistics based on ‘one-out’ (n-1 studies) sensitivity analysis indicating to what extent the overall heterogeneity changes by excluding a particular study at a time.

Furthermore, the "metaplot" command generates a table in the “Results window” of the Stata including more details about ‘one-out’ sensitivity analysis in terms of the I² and χ² statistics and their P-values. In addition to study codes, the studies’ identifications can be presented in the table.

The "metaplot" command is flexible and works with any measurement option including binary data (effect size + standard error or effect size + confidence intervals) and continuous data (sample + mean + standard deviation). The full form of the "metaplot" command is as follows

metaplot varlist [if] [in] [, id(study) tr(#)]

where

“varlist” can be “a b c d” or “lnes se” or “es lles ules” or “n1 mean1 sd1 n0 mean0 sd0”
“id(study)” option displays studies identifications (the first authors and the year of publication) specified by the variable “study” in the dataset.
“tr(#)” option specifies the desired threshold values for example: 0.4, 0.5, 0.6, 0.65, 0.8, etc.

The abbreviations in the above command represent the following terms.

“a b c d” represents “events” and “non-events” in the intervention (exposure) and control groups, respectively.
“lnes” represents the “Naperian logarithm” of the effect size that may be risk ratio (lnrr) or odds ratio (lnor).
“se” represents the standard error of the effect size.
“es” represents the effect size that may be risk ratio (rr) or odds ratio (or).
“lles” represents the lower limit of the confidence interval for the effect size.
“ules” represents the upper limit of the confidence interval for the effect size.
“n1” and “n0” represent the sample size for the intervention (exposure) and control groups, respectively.
“mean1” and “mean0” represent the mean for the intervention (exposure) and control groups, respectively.
“sd1” and “sd0” represent the standard deviation for the intervention (exposure) and control groups, respectively.

The relevant files including “metaplot.ado” and “metaplot.hlp” are attached to this paper as (S1 and S2 Files).

Results

To show the capability and flexibility of the ’metaplot" command we used various datasets (S1–S3 Datasets) related to our previous published meta-analyses [6–8].

The first dataset (S1 Dataset), which was used to introduce the "metaplot" module, related to a published meta-analysis addressed the risk factors for stomach cancer [6]. This is a dataset with a “binomial” outcome (stomach cancer). In this meta-analysis, 15 studies addressed the association between stomach cancer and drinking black tea. The heterogeneity across studies was high (I² = 64.23%). To perform sensitivity analysis using the “metaplot” command for this dataset, we executed the following command in the Stata software.

metaplot es lles ules, id(study)

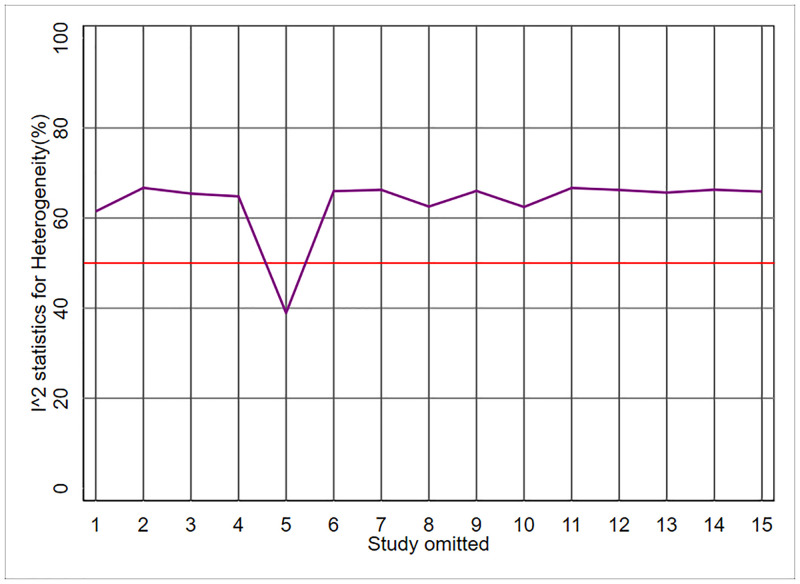
The result of the above command is given in Fig 1. This figure shows the results of the ‘one-out’ sensitivity analysis using the "metaplot" command. According to this figure, all values of I² statistics excluding one study at a time (n-1 studies) were above the desired threshold value of 50% except for study #5. By omitting study #5 from the meta-analysis, the heterogeneity fell below the desired threshold value of 50%. That means this study was an outlier and the main reason for heterogeneity across studies. Table 1 shows the results of ‘one-out’ sensitivity analysis in detail including I² and χ² statistics and their P-values omitting one study at a time. Based on this table, the overall heterogeneity across studies was high (I² = 64.23%). However, the heterogeneity decreased to 38.93% after omitting study #5.

Table 1. Meta-analyses of risk factors for stomach cancer; results of "metaplot" command.

Study omitted	I2	[95% Conf. Interval]		Chi2	P>\|t\|
1 Baroudi 2014	61.48	31.09	78.46	33.75	0.001
2 Takezaki 2001	66.71	41.62	81.02	39.05	0.000
3 Goldbohm 1996	65.43	39.06	80.39	37.60	0.000
4 Gallus 2009	64.81	37.83	80.09	36.95	0.000
5 Chew 1999	38.93	0.00	67.60	21.29	0.067
6 Watabe 1998	65.98	40.16	80.66	38.21	0.000
7 Inoue 1994	66.26	40.72	80.80	38.53	0.000
8 Hoshiyama 1992	62.55	33.27	78.98	34.71	0.001
9 Al-qadasl 2016	66.03	40.25	80.68	38.26	0.000
10 Hansson 1993	62.46	33.08	78.94	34.63	0.001
11 Galanis 1998	66.68	41.57	81.01	39.02	0.000
12 Chen 2009	66.23	40.67	80.78	38.50	0.000
13 Inoue 1998	65.65	39.50	80.50	37.85	0.000
14 Bao 2004	66.29	40.78	80.81	38.57	0.000
15 La Vecchia 1992	65.88	39.96	80.61	38.10	0.000
Combined	64.23	37.88	79.40	39.14	0.000

Open in a new tab

The second dataset (S2 Dataset), which was used to introduce the "metaplot" module, related to a published meta-analysis addressed the effect of oral potassium supplementation on the management of essential hypertension [7]. This is a dataset with a “continuous” outcome (blood pressure). In this meta-analysis, 22 studies addressed the effect of oral potassium supplementation on diastolic blood pressure. The heterogeneity across studies was high (I² = 81.88%). To perform sensitivity analysis using the “metaplot” command for this dataset, we executed the following command in the Stata software.

metaplot n1 mean1 sd1 n0 mean0 sd0, id(study)

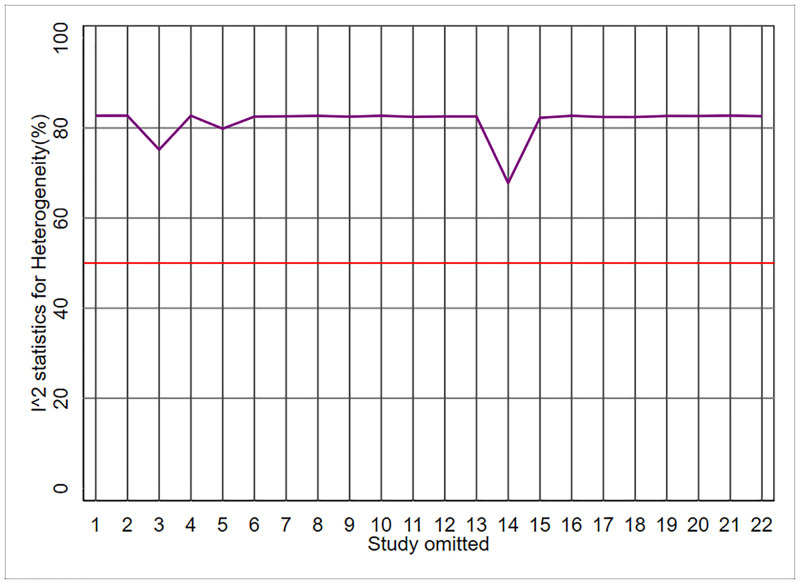
The result of the above command is given in Fig 2. This figure shows the results of the "metaplot" command based on a ‘one-out’ sensitivity analysis. According to this figure, all values of I² statistics excluding one study at a time (n-1 studies) were above the desired threshold value of 50%. However, the effect of omitting one study at a time was not similar across studies. For example, studies #14, #3, and #5 were responsible for the largest decrease in I² values, respectively. Although heterogeneity decreased significantly, particularly by omitting study #14, it did not reach below the threshold value of 50%. Therefore, this process should be repeated for a new set of n-1 studies after omitting study #14. According to the results of Table 2, the overall heterogeneity across studies was high (I² = 81.88%). However, the heterogeneity decreased to 67.76%, 75.19%, and 79.85% after omitting studies #14, #3, and #5, respectively.

Table 2. Meta-analyses of oral potassium supplementation for the management of essential hypertension; results of "metaplot" command.

Study omitted	I2	[95% Conf. Interval]		Chi2	P>\|t\|
1 Forrester 1988	82.72	74.64	88.23	115.74	0.000
2 Fotherby 1992	82.73	74.66	88.23	115.83	0.000
3 Franzoni 2005	75.19	62.10	83.75	80.60	0.000
4 Gijsbers 2015	82.73	74.65	88.23	115.79	0.000
5 Grimm 1988	79.85	69.93	86.49	99.24	0.000
6 Grobbee 1987	82.53	74.33	88.11	114.47	0.000
7 He 2010	82.60	74.44	88.15	114.92	0.000
8 Heseltine 1990	82.70	74.61	88.21	115.61	0.000
9 Kaplan 1985	82.51	74.30	88.10	114.37	0.000
10 Kawano 1998	82.72	74.64	88.23	115.75	0.000
11 Lawton 1990	82.47	74.23	88.07	114.09	0.000
12 MacGregor 1982	82.56	74.38	88.13	114.67	0.000
13 MacGregor 1984	82.56	74.38	88.13	114.67	0.000
14 Patki 199076	67.76	49.27	79.51	62.04	0.000
15 Rahimi 2007	82.25	73.88	87.94	112.71	0.000
16 Richards 1984	82.71	74.63	88.22	115.70	0.000
17 Siani 1987	82.43	74.17	88.05	113.82	0.000
18 Siani 1991	82.43	74.16	88.05	113.80	0.000
19 Smith 1985	82.67	74.56	88.19	115.40	0.000
20 Svetkey 1987	82.66	74.54	88.19	115.32	0.000
21 Valdes 1991	82.74	74.67	88.24	115.87	0.000
22 Wu 200682	82.62	74.47	88.16	115.05	0.000
Combined	81.88	73.51	87.6	115.88	0.000

Open in a new tab

The third dataset (S3 Dataset), which was used to introduce the "metaplot" module, related to a published meta-analysis addressed the preventable factors for primary prevention of childhood obesity [8]. This is a dataset with a “binomial” outcome (stomach cancer) and multiple studies. In this meta-analysis, 84 studies addressed the association between physical activity and childhood obesity. The heterogeneity across studies was high (I² = 96%). We used the sequential and combinatorial algorithm and performed a ‘one-out’ sensitivity analysis and repeated the process several times. For this purpose, we executed the following command in the Stata software for n-1 studies several times.

metaplot lnor se, id(study)

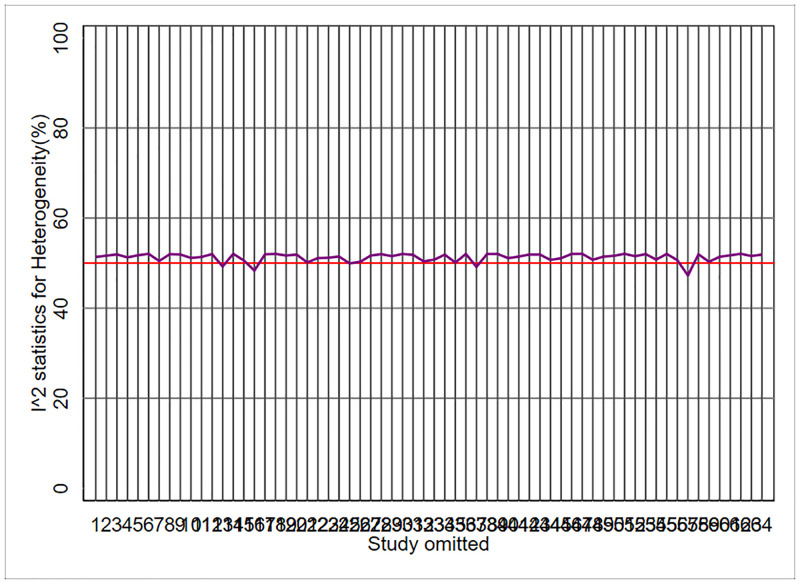
The result of the above command is given in Fig 3. This figure shows the last step when the I² statistic dropped below the desired threshold value of 50% by omitting just one more study. By looking at Fig 3 one can realize that there are at least 5 options to reduce the I² statistic below the value of 50%. By omitting any of the studies #13, #16, #25, #37, and #57 the I² statistic drops below the value of 50% and reaches 49.25%, 48.35%, 49.95%, 49.16%, and 47.25%, respectively (Table 3). When there is a possibility that more than one omitted study can result in I² dropping below the intended threshold, the study that results in the maximum decrease in the I² statistic below the desired threshold is selected. Accordingly omitting study #57 is the best choice. There might have been a chance that two or more studies caused the same reduction in I² by their exclusion. In that case, the study with the largest reduction in χ² statistic (the least χ² statistic) would have been dropped out.

Table 3. Meta-analyses of primary prevention of childhood overweight and obesity by preventable behavioral factors; results of "metaplot" command.

Study omitted	I2	[95% Conf. Interval]		Chi2	P>t
1 Adachi-Mejia 2007	51.36	35.01	63.59	127.46	0.000
2 Al-Domi 2019	51.65	35.43	63.79	128.22	0.000
3 Al-Hazzaa 2012	51.93	35.83	63.99	128.98	0.000
4 Al-Muhaimeed 2015	51.27	34.88	63.53	127.23	0.000
5 Arango 2011	51.74	35.56	63.86	128.47	0.000
6 Badr 2017	52.06	36.01	64.08	129.32	0.000
7 Basterfield 2014	50.47	33.74	62.98	125.17	0.000
8 Bhuiyan 2013	51.97	35.89	64.02	129.09	0.000
9 Bibiloni 2010	51.91	35.80	63.97	128.92	0.000
10 Boričić 2014	51.15	34.71	63.45	126.92	0.000
11 De Lucinéia 2014	51.36	35.02	63.60	127.48	0.000
12 Dudas 2008	52.00	35.93	64.03	129.15	0.000
13 Duncan 2011	49.25	31.99	62.13	122.16	0.000
14 Dupuy 2011	52.06	36.02	64.08	129.33	0.000
15 Eker 2018	50.59	33.91	63.06	125.48	0.000
16 Fu 2004	48.35	30.70	61.51	120.04	0.000
17 Gharib 2008	51.94	35.85	64.00	129.01	0.000
18 Ghosh 2015	52.04	35.99	64.07	129.28	0.000
19 Godakanda 2018	51.69	35.49	63.82	128.34	0.000
20 Ha 2005	51.88	35.77	63.96	128.86	0.000
21 Hajian-Tilaki 2012	50.15	33.28	62.76	124.38	0.000
22 Haug 2009	51.10	34.65	63.41	126.80	0.000
23 Honório 2014	51.19	34.77	63.47	127.01	0.000
24 Januszek-Trzciakowska 2014	51.46	35.16	63.67	127.74	0.000
25 Keane 2017	49.95	32.99	62.61	123.87	0.000
26 Kuhle 2010	50.28	33.47	62.84	124.70	0.000
27 Leatherdale 2013	51.68	35.47	63.81	128.31	0.000
28 Liu 2012	51.98	35.90	64.02	129.11	0.000
29 Lowry 2012	51.54	35.27	63.72	127.93	0.000
30 Lätt 2015	52.02	35.96	64.05	129.23	0.000
31 Macwana 2017	51.84	35.70	63.92	128.73	0.000
32 Mahfouz 2011	50.38	33.61	62.91	124.95	0.000
33 Mansoori 2018	50.75	34.15	63.17	125.90	0.000
34 Melkevik 2015	51.87	35.75	63.95	128.83	0.000
35 Muntaner-Mas 2017	50.12	33.23	62.73	124.29	0.000
36 Mushtaq 2011	52.04	35.98	64.06	129.26	0.000
37 Nasreddine 2014	49.16	31.86	62.07	121.95	0.000
38 Neutzling 2003	52.02	35.96	64.05	129.22	0.000
39 Oellingrath 2017	52.02	35.97	64.06	129.23	0.000
40 Oliveira 2017	51.10	34.64	63.41	126.79	0.000
41 Orgiles 2014	51.45	35.14	63.65	127.70	0.000
42 Ortega 2007	51.91	35.80	63.97	128.91	0.000
43 Panagiotakos 2008	51.90	35.79	63.97	128.90	0.000
44 Pati 2014	50.69	34.06	63.13	125.75	0.000
45 Peart 2011	51.08	34.61	63.40	126.73	0.000
46 Peltzer 2011	52.03	35.98	64.06	129.26	0.000
47 Pengpid 2018	52.06	36.02	64.08	129.34	0.000
48 Rani 2013	50.73	34.12	63.16	125.85	0.000
49 Rosi 2017	51.44	35.14	63.65	127.69	0.000
50 Saikia 2016	51.61	35.37	63.77	128.13	0.000
51 Savva 2002	52.06	36.02	64.08	129.33	0.000
52 Scanferla de Siqueira 2007	51.52	35.25	63.71	127.90	0.000
53 Shankaran 2011	52.00	35.93	64.04	129.16	0.000
54 Silva 2016	50.79	34.19	63.20	125.98	0.000
55 Silveira 2006	52.04	35.99	64.06	129.27	0.000
56 Teo 2014	50.64	33.99	63.10	125.62	0.000
57 Thibault 2010	47.25	29.11	60.75	117.54	0.000
58 Urrutia-Rojas 2008	51.94	35.85	64.00	129.02	0.000
59 Veugelers 2005	50.30	33.49	62.86	124.74	0.000
60 Watharkar 2015	51.41	35.08	63.63	127.59	0.000
61 Wethington 2013	51.72	35.53	63.84	128.42	0.000
62 Wilkie 2016	52.06	36.02	64.08	129.33	0.000
63 Winkvist 2016	51.58	35.33	63.74	128.04	0.000
64 Wittmeier 2008	51.89	35.77	63.96	128.86	0.000
Combined	51.29	35.06	63.46	129.34	0.000

Open in a new tab

Discussion

The idea of Metaplot, which was first introduced in 2010 [9], is a simple graphical approach to identify outliers and their effects on overall heterogeneity across studies. Patsopoulos et al. [5] suggested the sequential and combinatorial algorithm for performing sensitivity analyses. This algorithm is a useful method for assessing, exploring, and reporting the between-study heterogeneity in the meta-analysis but is time-consuming when the number of included studies is large and heterogeneity is substantial. For example, as noted in the results section, 84 studies addressed the association between physical activity and childhood obesity [8]. In this case, the sequential and combinatorial algorithm needs to be repeated hundreds of times particularly when the heterogeneity across studies is substantial. While by executing the "metaplot" command we can perform ‘one-out’ sensitivity analysis across several studies, no matter how many they are, and identify immediately to what extent the overall heterogeneity changes by excluding a particular study at a time. Another capability of the "metaplot" command is its flexibility. It is possible to execute this command for meta-analysis of different types of outcome data (e.g. binary, continuous, or time to event) and different types of summary measures (e.g. odds ratio, risk ratio, rate ratio, or hazard ratio).

The I² threshold value of 50% usually depends on the type of research we are performing. The threshold value of 50% is not rigid in the "metaplot" command. A rigid threshold value for the interpretation of I² can be misleading since the importance of inconsistency depends on several factors [1]. The "metaplot" command has the option "tr(#)" that establishes different threshold values.

Care must be taken in the interpretation of the chi-squared test since it has low power in the situation of a meta-analysis when studies have a small sample size or are few in number. This means that while a statistically significant result may indicate a problem with heterogeneity, a non-significant result must not be taken as evidence of no heterogeneity [1]. This is also why a P-value of 0.10 is sometimes used, rather than the conventional level of 0.05. Another problem with the test is that when there are many studies in a meta-analysis, the test has a high power to detect a small amount of heterogeneity that may be clinically unimportant.

Huedo-Medina et al. [10] examined and compared the performances of the Q test and the I² index for assessing homogeneity across individual studies in meta-analysis. They confirmed that the Q test only reports the presence or absence of homogeneity across studies but does not specify the extent of such heterogeneity. On the other hand, the I² index can quantify the degree of heterogeneity. Although the I² index has the same problems of low statistical power with a small number of studies, they suggested the I² index as a complement to the Q test.

The raw idea of “metaplot” was first introduced in 2010 [9]. This preliminary idea was never implemented actually at that time because the package had not been generated yet. The new design of the “metaplot” presented in this paper is very different from the original one introduced in 2010. The original design was a complicated three-dimensional graph with x, y, and z axes including unnecessary information. It was rather hard to understand. The new design of “metaplot” is a two-dimensional graph with x and y axes. Furthermore, we added a table including details of information (I² and χ² statistics and their P-values omitting one study in each turn) to simplify the interpretation of the ‘metaplot’ graph. In the current paper, we explained the capability of the “Metaplot” module and how to use the Stata command and its options. We examined this module on different real datasets and reported the results.

There are several graphical methods for the exploration of heterogeneity in the meta-analysis. One of these methods is the traditional Galbraith plot [11, 12]. This plot provides a graphical display to get a visual impression of the amount of heterogeneity from a meta-analysis. For each study, the observed effect sizes on the vertical axis are plotted against the reciprocal standard errors on the horizontal axis. The regression line projects through the origin, with its 95% confidence interval positioned 2 units over and below the regression line, has a slope equal to the overall log rate ratio. In the absence of heterogeneity, we could expect all the points to lie within the confidence bounds. The L’Abbé plot is another useful method for assessing heterogeneity in the meta-analysis [13, 14]. It is a scatter plot with the risk in the control group on the x-axis and the risk in the experimental group on the y-axis. The visual inspection gives a quick and easy indication of the studies having different results from other studies. These studies are considered outliers and hence potential sources of heterogeneity. Although these graphical procedures are useful and their interpretations are straightforward, they have a major limitation. When only one study causes extreme heterogeneity, these methods point to the same study as Metaplot suggests. However, in situations where the heterogeneity is resulted from several studies, the above graphical procedures are impractical to indicate to what extent a particular study influences the overall heterogeneity. Our proposed graphical method has overcome this problem. According to Metaplot method, one study is excluded from the meta-analysis at a time and the impact of the excluded study is evaluated on the overall heterogeneity. This ‘one-out’ approach tells us to what extent the overall heterogeneity changes by excluding a particular study at a time.

The Metaplot has a limitation. When the number of studies is very large (more than 35) as shown in Fig 3, the study codes in the x-axis come together and even may collapse due to space constraints. In such cases, the identification of the study codes may be difficult. Fortunately, the properties of the “metaplot” module solved this problem. In addition to the "Metaplot", this module generates a table in the “Results window” of the Stata and gives more details of ‘one-out’ sensitivity analysis including the I² and the χ² statistics and their P-values as well as the studies codes and the studies identifications. Therefore, by turning back to the “Results window” we can realize which study has the greatest impact on the overall heterogeneity based on the I² and χ² statistics.

Conclusion

Metaplot is a visual complementary approach for testing between-study heterogeneity. This plot is a simple graphical approach that gives a quick and easy identification of the studies having substantial influences on overall heterogeneity as fast as possible. This method is based on ‘one-out’ sensitivity analysis and provides information both graphically and quantitatively about the extent of the overall heterogeneity changes by excluding a particular study at a time in terms of I² and χ² statistics. It is possible to implement this graph for the meta-analysis of different types of outcome data.

Supporting information

S1 File

(ADO)

Click here for additional data file.^{(7.1KB, ado)}

S2 File

(HLP)

Click here for additional data file.^{(3KB, hlp)}

S1 Dataset

(DTA)

Click here for additional data file.^{(3.6KB, dta)}

S2 Dataset

(DTA)

Click here for additional data file.^{(5.6KB, dta)}

S3 Dataset

(DTA)

Click here for additional data file.^{(4.5KB, dta)}

Data Availability

All relevant data are within the manuscript and its Supporting information files.

Funding Statement

The Vice-Chancellor of Research and Technology, Hamadan University of Medical Sciences funded this study (No. 9603161751). However, the funder had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1.Higgins JPT, Green S. Cochrane handbook for systematic reviews of interventions. Chichester: John Wiley & Sons, Ltd; 2019. [Google Scholar]
2.Michael Borenstein V. Hedges L, Higgins JPT, Rothstein Hannah R. Introduction to Meta-Analysis. Chichester: John Wiley & Sons Ltd; 2009. [Google Scholar]
3.Higgins JPT, Thompson SG, Deeks JJ, Altman D. Measuring inconsistency in meta-analyses. BMJ. 2003;327:557–60. doi: 10.1136/bmj.327.7414.557 [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Glasziou PP, Sanders SL. Investigating causes of heterogeneity in systematic reviews. Stat Med. 2002;21:1503–11. doi: 10.1002/sim.1183 [DOI] [PubMed] [Google Scholar]
5.Patsopoulos NA, Evangelou E, Ioannidis JPA. Sensitivity of between-study heterogeneity in meta-analysis: proposed metrics and empirical evaluation. Int J Epidemiol. 2008;37:1148–57. doi: 10.1093/ije/dyn065 [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Poorolajal J, Moradi L, Mohammadi Y, Cheraghi Z, Gohari-Ensaf F. Risk factors for stomach cancer: a systematic review and meta-analysis. Epidemiol Health. 2020;42:e2020004. doi: 10.4178/epih.e2020004 [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Poorolajal J, Zeraati F, Soltanian AR, Sheikh V, Maleki A. Oral potassium supplementation for management of essential hypertension: A meta-analysis of randomized controlled trials. PloS One. 2017;12(4):e0174967. doi: 10.1371/journal.pone.0174967 [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Poorolajal J, Sahraei F, Mohamdadi Y, Doosti-Irani A, Moradi L. Behavioral factors influencing childhood obesity: a systematic review and meta-analysis. Obes Res Clin Pract. 2020;14:109–18. doi: 10.1016/j.orcp.2020.03.002 [DOI] [PubMed] [Google Scholar]
9.Poorolajal J, Fotouhi A, Majdzadeh R, Mahmoodi M. MetaPlot: a novel Stata graph for assessing heterogeneity at a glance. Iran J Public Health. 2010;39(2):102–4. [PMC free article] [PubMed] [Google Scholar]
10.Huedo-Medina TB, Sánchez-Meca J, Marín-Martínez F, Botella J. Assessing heterogeneity in meta-analysis: Q statistic or I2 index? Psychological methods. 2006;11(2):193–206. 16784338. doi: 10.1037/1082-989X.11.2.193 [DOI] [PubMed] [Google Scholar]
11.Galbraith RF. Graphical display of estimates having differing standard errors. Technometrics. 1988a;30(3):271–81. [Google Scholar]
12.Galbraith RF. A note on graphical presentation of estimated odds ratios from several clinical trials. Stat Med. 1988b;7:889–94. [DOI] [PubMed] [Google Scholar]
13.Deeks JJ. Issues in the selection of a summary statistic for meta-analysis of clinical trials with binary outcomes. Stat Med. 2002;21:1575–600. doi: 10.1002/sim.1188 [DOI] [PubMed] [Google Scholar]
14.L’Abbé KA, Detsky AS, O’Rourke K. Meta-analysis in clinical research. Ann Intern Med. 1987;107:224–33. doi: 10.7326/0003-4819-107-2-224 [DOI] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0253341.r001

Decision Letter 0

Mohammad Asghari Jafarabadi

14 Apr 2021

PONE-D-21-06251

Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis

PLOS ONE

Dear Dr. Poorolajal,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Please submit your revised manuscript by May 29 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.

We look forward to receiving your revised manuscript.

Kind regards,

Mohammad Asghari Jafarabadi

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Please review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript. If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

3. Please include captions for your Supporting Information files at the end of your manuscript, and update any in-text citations to match accordingly. Please see our Supporting Information guidelines for more information: http://journals.plos.org/plosone/s/supporting-information

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: Author may add the reference to the work done by Huedo-Medina, T. B., Sánchez-Meca, J., Marín-Martínez, F., & Botella, J. (2006). Assessing heterogeneity in meta-analysis: Q statistic or I² index?. Psychological methods, 11(2), 193.”

The author has used illogically his 3 papers in the reference.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2021 Jun 28;16(6):e0253341. doi: 10.1371/journal.pone.0253341.r002

Author response to Decision Letter 0

15 Apr 2021

Editor’s comments

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.

Answer: Done

A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.

Answer: Done

An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

Answer: Done

Reviewers' comments:

Reviewer #1

Author may add the reference to the work done by Huedo-Medina, T. B., Sánchez-Meca, J., Marín-Martínez, F., & Botella, J. (2006). Assessing heterogeneity in meta-analysis: Q statistic or I² index?. Psychological methods, 11(2), 193.”

Answer: We added a paragraph in the discussion section and explain the results of this paper.

The author has used illogically his 3 papers in the reference.

Answer: You are right. The topics of these papers are not relevant to the topic of the current manuscript. However, we used real data from our previously published studies. We gave reference to these studies to indicate the reality of the data and their originality. However, if the honorable reviewers insist, we will remove these papers from the reference list.

Thank you.

PLoS One. doi: 10.1371/journal.pone.0253341.r003

Decision Letter 1

Mohammad Asghari Jafarabadi

18 May 2021

PONE-D-21-06251R1

Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis

PLOS ONE

Dear Dr. Poorolajal,

Please submit your revised manuscript by Jul 02 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Mohammad Asghari Jafarabadi

Academic Editor

PLOS ONE

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: N/A

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: (No Response)

Reviewer #2: The authors present a STATA module for assessing heterogeneity in a meta analysis using a "one out" sensitivity analysis. An advantage of this package is that it makes trivial what can be an extremely tedious process. This module likely has utility for some researchers conducting meta analyses and I believe that providing peer reviewed documentation for modules like these is good practice.

However, what the authors present is not a new module but appears to be a modification of an existing module (on which they published a paper in The Iranian Journal of Public Health in 2010). If I understand the manuscript correctly, the primary changes made to the old model were to modify plot generation so that it created a more interpretable figure and to include a table that summarized the relevant statistics of each iteration. The original module is not mentioned in the manuscript until halfway through the discussion section. If there are other key differences, they are not discussed in the manuscript.

I do not believe that this manuscript introduces sufficient new information (or introduces old information in a sufficiently more comprehensive or accessible manner) to warrant a full research article. The relevant new information introduced might be better suited as patch notes for the original module. If the authors wrote a different paper, one which focused on the changes made to the package and how those changes impact interpretation/conclusions, I could see that paper being more valuable.

Additional comments in attachment.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Attachment

Submitted filename: Poorolajal et al - reviewer comments.pdf

Click here for additional data file.^{(140.1KB, pdf)}

PLoS One. 2021 Jun 28;16(6):e0253341. doi: 10.1371/journal.pone.0253341.r004

Author response to Decision Letter 1

18 May 2021

Reviewer comments: "Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis"

Sections quoted from the manuscript are in red.

2021-05-07

• Title

Is this actually a new Stata module or an update of the older Metaplot module? If it is the latter, language should be changed accordingly.

Answer: This Stata module is generated for the first time. The paper that we published in 2010 ONLY introduced the IDEA of Metaplot. But we did not generate the Stata module at that time. It took a long time until we could generate the module actually in the present form and ready for practice.

• Abstract

Results: first sentence presupposes that there is one study causing heterogeneity when that may or may not be the case. Consider instead: Metaplot allows rapid identification of studies that have a disproportionate impact on heterogeneity across studies, and communicates to what extent omission of that study may reduce the overall heterogeneity based on the I2 and χ2 statistics.

Answer: We replaced the first sentence with the suggested sentence. Thank you.

Results: I'm not sure these are so much results as an assertion as to what the authors believe Metaplot can do. It might be better to overview the performance of Metaplot in the practical examples here.

Answer: This module was tested on real datasets with both “binomial” and “continuous” outcomes. Table 1 is an example of the real dataset with a “binomial” outcome (stomach cancer). Table 2 is another example of a real dataset with a “continuous” outcome (blood pressure). Table 2 is the third example of a real dataset with a binomial outcome (childhood obesity) with multiple studies. Therefore, this module can work in any situation (either limited or multiple studies) and with any outcome (either binomial or continuous). To clarify this ambiguity, we specified the type of outcomes in the results section.

• Introduction

Your opening sentence is made a bit awkward by the inclusion of a non-defining clause where a defining clause should be used. Easily fixed by changing it to: The studies that are brought together in a meta-analysis inevitably differ in many aspects.

Answer: We replaced the opening sentence with the suggested sentence. Thank you.

• Methods

Potential typo at the bottom of page 3. Language is referred to as "Meta" but functions are called "Mata" functions. I'm not a Stata user so please ignore this comment if my understanding is incorrect.

Answer: The correct form of the word is “Mata”. Thank you.

Is the first paragraph introducing mata functions even necessary given that you don't use or discuss this information later in the paper?

Answer: You are right. It is not necessary. Therefore, we deleted the first paragraph from the methods section.

• Discussion

Performing sensitivity analyses based on the sequential and combinatorial algorithm proposed by Patsopoulos et al [5]. This is a sentence fragment and should be corrected.

Answer: We corrected the sentence as follows: “Patsopoulos et al [5] suggested the sequential and combinatorial algorithm for performing sensitivity analyses.”

"boring," subjective judgement. "Time consuming" is sufficient. Consider exclusion.

Answer: The word “boring’ was removed.

Although “metaplot” was first introduced in 2010[10], however, it was a preliminary idea that changed a lot over time. "However" can be removed here.

Answer: The word “however’ was removed.

Although “metaplot” was first introduced in 2010[10], however, it was a preliminary idea that changed a lot over time. The new design of the “metaplot” presented in this paper is very different from the original one introduced in 2010. The original design was a complicated three-dimensional graph with x, y, and z axes including unnecessary information. It was rather hard to understand. The new design of “metaplot” is a two-dimensional graph with x and y axes. Furthermore, we added a table including details of information (I2 and χ2 statistics and their P-values omitting one study in each turn) to simplify the interpretation of the ‘metaplot’ graph.

So what this paper is actually introducing is a modification to an existing package? If I'm understanding this paragraph correctly, the updated package is using fundamentally the same methodology but provides a changed graphical output and additional tables that improve ease of interpretation. While I support providing peer reviewed documentation for statistical packages that can be cited in papers that use the package, I don't think that this manuscript introduces sufficient new information (or introduces old information in a sufficiently more comprehensive or accessible manner) to warrant a full research article. This feels like something that could be attached to the patch notes for the package.

Answer: In the paper that we published in 2010, we only introduced the raw idea of “Metaplot”. We never generated a package for practice. After the publication of the paper, several researchers from around the world contacted me and requested to submit the Stata module for them, but I apologized to them because there was no Stata module at that time. This idea was in my mind until now (after ten years) that I could find an expert software engineer (my coauthor Shahla) who helped me to generate the Stata module. During this process, we changed the preliminary idea and improved its potential capability in the present form. In 2010, we prepared the figure manually by Excel software to present our subjective idea. The appearance of the figure introduced in 2010 is completely different from what we produced now by the Stata module. In the current paper, we explained the capability of the “Metaplot” module and how to use the Stata command and its options. We examined this module, which we generated recently, on different real datasets and reported the results in Tables 1-3 and Figures 1-3. We added an explanation to the discussion section to clarify this ambiguity.

*******************

Reviewer #2:

The authors present a STATA module for assessing heterogeneity in a meta analysis using a "one out" sensitivity analysis. An advantage of this package is that it makes trivial what can be an extremely tedious process. This module likely has utility for some researchers conducting meta analyses and I believe that providing peer reviewed documentation for modules like these is good practice.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(21.5KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0253341.r005

Decision Letter 2

Mohammad Asghari Jafarabadi

3 Jun 2021

Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis

PONE-D-21-06251R2

Dear Dr. Poorolajal,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Mohammad Asghari Jafarabadi

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

The references should be set according to the journal style using a reference manager.

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

Reviewer #3: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #3: Partly

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #3: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #3: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #3: Yes

**********

6. Review Comments to the Author

Reviewer #3: Everything is okayو The method of writing the research is good and the way to describe the results is good, but it needs to arrange the sources in one of the source ranking programs such as Mendeley

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #3: No

PLoS One. doi: 10.1371/journal.pone.0253341.r006

Acceptance letter

Mohammad Asghari Jafarabadi

17 Jun 2021

PONE-D-21-06251R2

Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis

Dear Dr. Poorolajal:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Professor Mohammad Asghari Jafarabadi

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 File

(ADO)

Click here for additional data file.^{(7.1KB, ado)}

S2 File

(HLP)

Click here for additional data file.^{(3KB, hlp)}

S1 Dataset

(DTA)

Click here for additional data file.^{(3.6KB, dta)}

S2 Dataset

(DTA)

Click here for additional data file.^{(5.6KB, dta)}

S3 Dataset

(DTA)

Click here for additional data file.^{(4.5KB, dta)}

Attachment

Submitted filename: Poorolajal et al - reviewer comments.pdf

Click here for additional data file.^{(140.1KB, pdf)}

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(21.5KB, docx)}

Data Availability Statement

All relevant data are within the manuscript and its Supporting information files.

[pone.0253341.ref001] 1.Higgins JPT, Green S. Cochrane handbook for systematic reviews of interventions. Chichester: John Wiley & Sons, Ltd; 2019. [Google Scholar]

[pone.0253341.ref002] 2.Michael Borenstein V. Hedges L, Higgins JPT, Rothstein Hannah R. Introduction to Meta-Analysis. Chichester: John Wiley & Sons Ltd; 2009. [Google Scholar]

[pone.0253341.ref003] 3.Higgins JPT, Thompson SG, Deeks JJ, Altman D. Measuring inconsistency in meta-analyses. BMJ. 2003;327:557–60. doi: 10.1136/bmj.327.7414.557 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0253341.ref004] 4.Glasziou PP, Sanders SL. Investigating causes of heterogeneity in systematic reviews. Stat Med. 2002;21:1503–11. doi: 10.1002/sim.1183 [DOI] [PubMed] [Google Scholar]

[pone.0253341.ref005] 5.Patsopoulos NA, Evangelou E, Ioannidis JPA. Sensitivity of between-study heterogeneity in meta-analysis: proposed metrics and empirical evaluation. Int J Epidemiol. 2008;37:1148–57. doi: 10.1093/ije/dyn065 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0253341.ref006] 6.Poorolajal J, Moradi L, Mohammadi Y, Cheraghi Z, Gohari-Ensaf F. Risk factors for stomach cancer: a systematic review and meta-analysis. Epidemiol Health. 2020;42:e2020004. doi: 10.4178/epih.e2020004 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0253341.ref007] 7.Poorolajal J, Zeraati F, Soltanian AR, Sheikh V, Maleki A. Oral potassium supplementation for management of essential hypertension: A meta-analysis of randomized controlled trials. PloS One. 2017;12(4):e0174967. doi: 10.1371/journal.pone.0174967 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0253341.ref008] 8.Poorolajal J, Sahraei F, Mohamdadi Y, Doosti-Irani A, Moradi L. Behavioral factors influencing childhood obesity: a systematic review and meta-analysis. Obes Res Clin Pract. 2020;14:109–18. doi: 10.1016/j.orcp.2020.03.002 [DOI] [PubMed] [Google Scholar]

[pone.0253341.ref009] 9.Poorolajal J, Fotouhi A, Majdzadeh R, Mahmoodi M. MetaPlot: a novel Stata graph for assessing heterogeneity at a glance. Iran J Public Health. 2010;39(2):102–4. [PMC free article] [PubMed] [Google Scholar]

[pone.0253341.ref010] 10.Huedo-Medina TB, Sánchez-Meca J, Marín-Martínez F, Botella J. Assessing heterogeneity in meta-analysis: Q statistic or I2 index? Psychological methods. 2006;11(2):193–206. 16784338. doi: 10.1037/1082-989X.11.2.193 [DOI] [PubMed] [Google Scholar]

[pone.0253341.ref011] 11.Galbraith RF. Graphical display of estimates having differing standard errors. Technometrics. 1988a;30(3):271–81. [Google Scholar]

[pone.0253341.ref012] 12.Galbraith RF. A note on graphical presentation of estimated odds ratios from several clinical trials. Stat Med. 1988b;7:889–94. [DOI] [PubMed] [Google Scholar]

[pone.0253341.ref013] 13.Deeks JJ. Issues in the selection of a summary statistic for meta-analysis of clinical trials with binary outcomes. Stat Med. 2002;21:1575–600. doi: 10.1002/sim.1188 [DOI] [PubMed] [Google Scholar]

[pone.0253341.ref014] 14.L’Abbé KA, Detsky AS, O’Rourke K. Meta-analysis in clinical research. Ann Intern Med. 1987;107:224–33. doi: 10.7326/0003-4819-107-2-224 [DOI] [PubMed] [Google Scholar]

PERMALINK

Metaplot: A new Stata module for assessing heterogeneity in a meta-analysis

Jalal Poorolajal

Shahla Noornejad

Roles

Abstract

Background

Method

Results

Conclusions

Introduction

Methods

Results

Fig 1. Meta-analyses of risk factors for stomach cancer; metaplot delineates I2 statistics and χ2 statistics and their P-values based on ‘one-out’ sensitivity analysis [Stata command: Metaplot es lles rules, id(study)].

Table 1. Meta-analyses of risk factors for stomach cancer; results of "metaplot" command.

Fig 2. Meta-analyses of oral potassium supplementation for the management of essential hypertension; metaplot delineates I2 statistics and χ2 statistics and their P-values based on ‘one-out’ sensitivity analysis [Stata command: Metaplot n1 mean1 sd1 n0 mean0 sd0, id(study)].

Table 2. Meta-analyses of oral potassium supplementation for the management of essential hypertension; results of "metaplot" command.

Fig 3. Meta-analyses of primary prevention of childhood overweight and obesity by preventable behavioral factors; metaplot delineates I2 statistics and χ2 statistics and their P-values based on ‘one-out’ sensitivity analysis [Stata command: Metaplot lnor se, id(study)].

Table 3. Meta-analyses of primary prevention of childhood overweight and obesity by preventable behavioral factors; results of "metaplot" command.

Discussion

Conclusion

Supporting information

Data Availability

Funding Statement

References

Decision Letter 0

Mohammad Asghari Jafarabadi

Roles

Author response to Decision Letter 0

Decision Letter 1

Mohammad Asghari Jafarabadi

Roles

Author response to Decision Letter 1

Decision Letter 2

Mohammad Asghari Jafarabadi

Roles

Acceptance letter

Mohammad Asghari Jafarabadi

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Fig 1. Meta-analyses of risk factors for stomach cancer; metaplot delineates I² statistics and χ² statistics and their P-values based on ‘one-out’ sensitivity analysis [Stata command: Metaplot es lles rules, id(study)].

Fig 2. Meta-analyses of oral potassium supplementation for the management of essential hypertension; metaplot delineates I² statistics and χ² statistics and their P-values based on ‘one-out’ sensitivity analysis [Stata command: Metaplot n1 mean1 sd1 n0 mean0 sd0, id(study)].

Fig 3. Meta-analyses of primary prevention of childhood overweight and obesity by preventable behavioral factors; metaplot delineates I² statistics and χ² statistics and their P-values based on ‘one-out’ sensitivity analysis [Stata command: Metaplot lnor se, id(study)].