Learning the Protein Language: Evolution, Structure and Function

Abstract

Language models have recently emerged as a powerful machine learning approach for distilling information from massive protein sequence databases. From readily available sequence data alone, these models discover evolutionary, structural, and functional organization across protein space. Using language models, we can encode amino acid sequences into distributed vector representations that capture their structural and functional properties as well as evaluate the evolutionary fitness of sequence variants. We discuss recent advances in protein language modeling and their applications to downstream protein property prediction problems. We then consider how these models can be enriched with prior biological knowledge and introduce an approach for encoding protein structural knowledge into the learned representations. The knowledge distilled by these models allows us to improve downstream function prediction through transfer learning. Deep protein language models are revolutionizing protein biology. They suggest new ways to approach protein and therapeutic design. However, further developments are needed to encode strong biological priors into protein language models and to increase their accessibility to the broader community.

Introduction

Proteins are molecular machines that carry out the majority of the molecular function of cells. They are composed of linear sequences of amino acids which fold into complex ensembles of 3-dimensional structures, which can range from ordered to disordered and undergo conformational changes; biochemical and cellular functions emerge from protein sequence and structure. Understanding the sequence-structure-function relationship is the central problem of protein biology and is pivotal for understanding disease mechanisms and designing proteins and drugs for therapeutic and bioengineering applications.

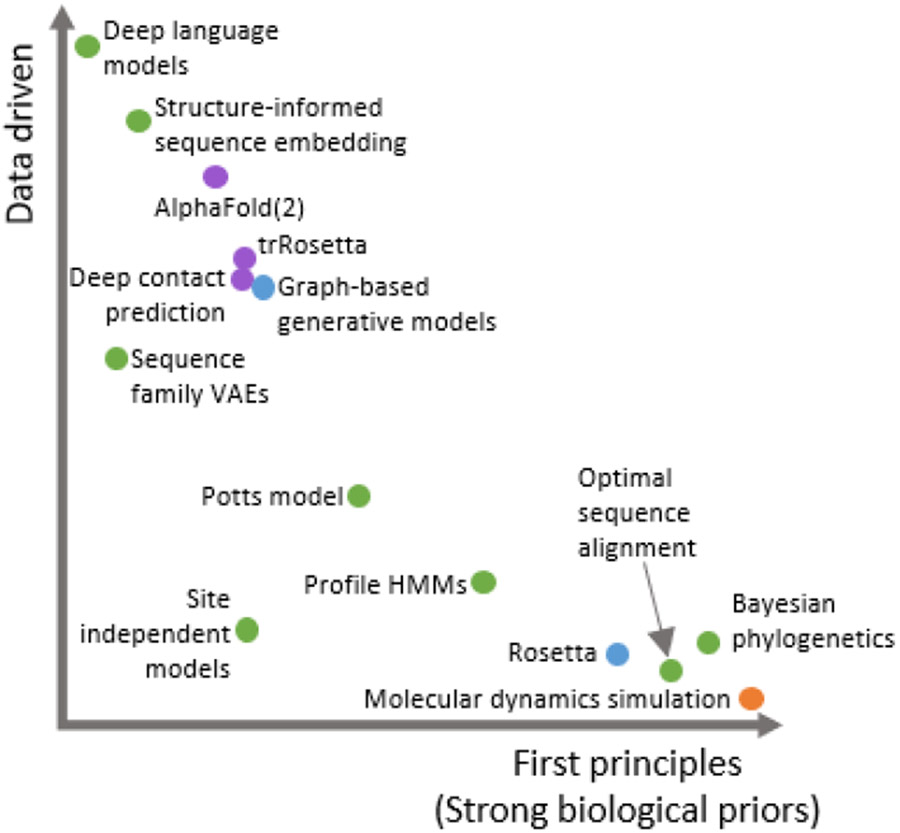
The complexity of the sequence-structure-function relationship continues to challenge our computational modeling ability, in part because existing tools do not fully realize the potential of the increasing quantity of sequence, structure, and functional information stored in large databases. Until recently, computational methods for analyzing proteins have used either first principles-based structural simulations or statistical sequence modeling approaches that seek to identify sequence patterns that reflect evolutionary, and therefore functional, pressures ^1-5 (Figure 1). Within these methods, structural analysis has been largely first principles driven while sequence analysis methods are primarily based on statistical sequence models, which make strong assumptions about evolutionary processes, but have become increasingly data driven with the growing amount of available natural sequence information.

Figure 1 ∣.

Two-dimensional schematic of some recent and classical methods in protein sequence and structure analysis, characterized by the extent to which the approach is motivated by first principles (strong biological priors) vs. driven by big data. We color methods by types of input-output pairs. Green: sequence-sequence, purple: sequence-structure, blue: structure-sequence, orange: structure-structure. Classical methods tend to be more strongly first principles driven while newer methods are increasingly data driven. Existing methods tend to be either data driven or first principles-based with few methods existing in between. *Note that, at this time, details of AlphaFold2 have not been made public, so placement in Figure 1 is a rough estimate. Some methods, especially Rosetta, can perform multiple functions.

Physics-based approaches use all atom energy functions ^6-8 or heuristics designed for proteins ⁹ to estimate the energy of a given conformation and simulate natural motions. These methods are appealing, because they draw on our fundamental understanding of the physics of these systems and generate interpretable hypotheses. The Rosetta tool, which stitches together folded fragments associated with small constant-size contiguous subsequences, has been remarkably successful in its use of free energy estimation for protein folding and design ¹⁰, and molecular dynamics software such as GROMACS are widely used for modeling dynamics and fine-grained structure prediction ⁶. Statistical sampling approaches have also been developed that seek to sample from accessible conformations based on coarse grained energy functions ^11-13. Rosetta has been especially successful for solving the design problem by using a mix of structural templates and free energy minimization to find sequences that match a target structure. However, despite Rosetta’s successes, it and similar approaches assume simplified energy models, are extremely computationally expensive, require expert knowledge to set up correctly, and have limited accuracy.

At the other end of the spectrum, statistical sequence models have proven extremely useful for modeling the amino acid sequences of related sets of proteins. These methods allow us to discover constraints on amino acids imposed by evolutionary pressures and are widely used for homology search ^9,14-17 and for predicting residue-residue contacts in the 3D protein structure using covariation between amino acids at pairs of positions in the sequence (coevolution)^1,2,18-24. Advances in protein structure prediction have been driven by building increasingly large deep learning systems to predict residue-residue distances from sequence families ^3,25 and fold proteins based on the predicted distance constraints which culminated recently in the success of AlphaFold2 at the Critical Assessment of protein Structure Prediction (CASP) 14 competition ²⁶. These methods rely on large datasets of protein sequences that are similar enough to be aligned with high confidence but contain enough divergence to confidently infer statistical couplings between positions. Accordingly, they are unable to learn patterns across large-scale databases of possibly unrelated proteins and have limited ability to draw on the increasing structure and function information available.

Language models have recently emerged as a powerful paradigm for generative modeling of sequences and as a means to learn “content-aware” data representations from large-scale sequence datasets. Statistical language models are probability distributions over sequences of tokens (e.g. words or characters in natural language processing, amino acids for proteins). Given a sequence of tokens, a language model assigns a probability to the whole sequence. In natural language processing (NLP), language models are widely used for machine translation, question-answering, and information retrieval amongst other applications. In biology, profile Hidden Markov Models (HMMs) are simple language models that are already widely used for homology modeling and search. Language models capture complex dependencies between amino acids and can be trained on all protein sequences rather than being focused on individual families; in doing so, they have the potential to push the limits of statistical sequence modeling. In bringing these models to biology, we now not only have the ability to learn from naturally observed sequences, including across all of known sequence space ^27,28, but are also able to incorporate existing structural and functional knowledge through multi-task learning. Language models learn the probability of a sequence occurring and this can be directly applied to predict the fitness of sequence mutations ^29-31 . They also learn summary representations, powerful features that can be used to better capture sequence relationships and link sequence to function via transfer learning ^27,28,32-35. Finally, language models also offer the potential for controlled sequence generation by conditioning the language model on structural³⁶ or functional ³⁷ specifications.

Deep language models are an exciting breakthrough in protein sequence modeling, allowing us to discover aspects of structure and function from only the evolutionary relationships present in a corpus of sequences. However, the full potential of these models has not been realized as they continue to benefit from more parameters, more compute power, and more data. At the same time, these models can be enriched with strong biological priors through multi-task learning.

Here, we propose that methods incorporating both large datasets and strong domain knowledge will be key to unlocking the full potential of protein sequence modeling. Specifically, physical structure-based priors can be learned through structure supervision while also learning evolutionary relationships from hundreds of millions of natural protein sequences. Furthermore, the evolutionary and structural relationships encoded allow us to learn functional properties of proteins through transfer learning. In this synergy, we will discuss these developments and present new results towards enriching large-scale language models with structure-based priors through multi-task learning. First, we will discuss new developments in deep learning and language modeling and their application to protein sequence modeling with large datasets. Second, we will discuss how we can enrich these models with structure supervision. Third, we will discuss transfer learning and demonstrate that the evolutionary and structural information encoded in our deep language models can be used to improve protein function prediction. Finally, we will discuss future directions in protein machine learning and large-scale language modeling.

Protein language models distill information from massive protein sequence databases

Language models for protein sequence representation learning (Figure 2) have seen a surge of interest following the success of large-scale models in the field of natural language processing (NLP). These models draw on the idea that distributed vector representations of proteins can be extracted from generative models of protein sequences, learned from a large and diverse database of sequences across natural protein space, and thus can capture the semantics, or function, of a given sequence. Here, function refers to any and all properties related to what a protein does. These properties are often subject to evolutionary pressures, because these functions must be maintained or enhanced in order for an organism to survive and reproduce. These pressures manifest in the distribution over amino acids present in natural protein sequences and, hence, are discoverable from large and diverse enough sets of naturally occurring sequences.

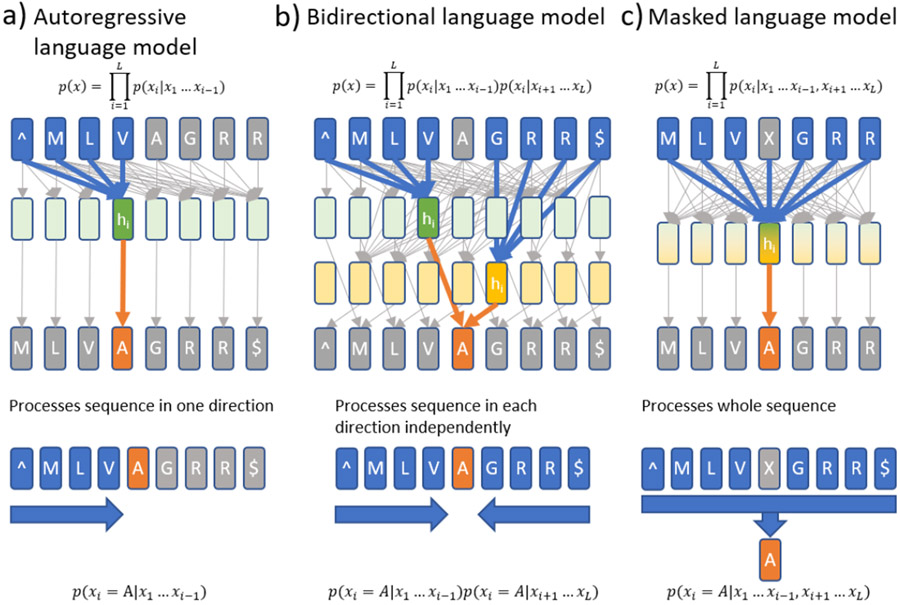
Figure 2 ∣.

Diagram of model architectures and language modeling approaches. a) Language models model the probability of sequences. Typically, this distribution is factorized over the sequence such that the probability of a token (e.g., amino acid) at position i (x_i) is conditioned on the previous tokens. In neural language models, this is achieved by first computing a hidden layer (h_i) given by the sequence up to position i-1 and then calculating the probability distribution over token x_i given h_i. In this example sequence, “^” and “$” represent start and stop tokens respectively and the sequence has length L. b) Bidirectional language models instead model the probability of a token conditioned on the previous and following tokens independently. For each token x_i, we compute a hidden layer using separate forward and reverse direction models. These hidden layers are then used to calculate the probability distribution over tokens at position i conditioned on all other tokens in the sequence. This allows us to extract representations that capture complete sequence context. c) Masked language models model the probability of tokens at each position conditioned on all other tokens in the sequence by replacing the token at each position with an extra “mask” token (“X”). In these models, the hidden layer at each position is calculated from all tokens in the sequence which allows the model to capture conditional non-independence between tokens on either side of the masked token. This formulation lends itself well to transfer learning, because the representations can depend on the full context of each token.

The ability to learn semantics emerges from the distributional hypothesis: tokens (e.g. words, amino acids) that occur in similar contexts tend to carry similar meanings. Language models only require sequences to be observed and are trained to model the probability distribution over amino acids using an autoregressive formulation (Figure 2a, 2b) or masked position prediction formulation (also called a cloze task in NLP, Figure 2c). In autoregressive language models, the probability of a sequence is factorized such that the probability of each token is conditioned only on the preceding tokens. This factorization is exact and is useful when sampling from the distribution or evaluating the probabilities themselves is of primary interest. The drawback to this formulation is that the representations learned for each position depend only on preceding positions, potentially making them less useful as contextual representations. The masked position prediction formulation (also known as masked language modeling) addresses this problem by considering the probability distribution over each token at each position conditioned on all other tokens in the sequence. The masked language modeling approach does not allow calculating correctly normalized probabilities of whole sequences but is more appropriate when the learned representations are the outcomes of primary interest. The unprecedented recent success of language models in natural language processing, e.g.Google’s BERT and OpenAI’s GTP-3, is largely driven by their ability to learn from billions of text entries in enormous online corpora. Analogously, we have natural protein sequence databases with 100s of millions of unique sequences that continue to grow rapidly.

Recent advances in NLP have been driven by innovations in neural network architectures, new training approaches, increasing compute power, and increasing accessibility of huge text corpuses. Several NLP methods have been proposed that draw on unsupervised, now often called self-supervised, learning ^38,39 to fit large-scale bidirectional long-short term recurrent neural networks (bidirectional LSTMs or biLSTMs) ^40,41 or Transformers ⁴² and its recent variants. LSTMs are recurrent neural networks. These models process sequences one token at a time in order and therefore learn representations that capture information from a position and all previous positions. In order to include information from tokens before and after any given position, bidirectional LSTMs combine two separate LSTMs operating in the forward and backward directions in each layer (e.g. as in Figure 2b). Although these models are able to learn representations including whole sequence context, their ability to learn distant dependencies is limited in practice. To address this limitation, transformers learn representations by explicitly calculating an attention vector over each position in the sequence. In the self-attention mechanism, the representation for each position is learned by “attending to” each position of the same sequence, well suited for masked language modeling (Figure 2c). In a self-attention module, the output representation of each element of a sequence is calculated as a weighted sum over transformations of the input representations at each position where the weighting itself is based on a learned transformation of the inputs. The attention mechanism is typically believed to allow transformers to learn dependencies between positions distant in the linear sequence more easily. Transformers are also useful as autoregressive language models.

In natural language processing, Peters et al. recognized that the hidden layers (intermediate representations of stack neural networks) of biLSTMs encoded semantic meaning of words in context. This observation has been newly leveraged for biological sequence analysis ^27,28 to learn more semantically meaningful sequence representations. The success of deep transformers for machine translation inspired their application to contextual text embedding, that is learning contextual vector embeddings of words and sentences, giving rise to the now widely used Bidirectional Encoder Representations from Transformers (BERT) model in NLP ³⁹. BERT is a deep transformer trained as a masked language model on a large text corpus. As a result, it learns contextual representations of text that capture contextual meaning and improve the accuracy of downstream NLP systems. Transformers have also demonstrated impressive performance as autoregressive language models, for example with the Generative Pre-trained Transformer (GPT) family of models ^43-45, which have made impressive strides in natural language generation. These works have inspired subsequent applications to protein sequences ^32,33,46,47.

Although transformers are powerful models, they require enormous numbers of parameters and train more slowly than typical recurrent neural networks. With massive scale datasets and compute and time budgets, transformers can achieve impressive results, but, generally, recurrent neural networks (e.g., biLSTMs) need less training data and less compute, so might be more suitable for problems where fewer sequences are available, such as training on individual protein families, or compute budgets are tight. Constructing language models that achieve high accuracy with better compute efficiency is an algorithmic challenge for the field. An advantage of general purpose pre-trained protein models is that we only need to do the expensive training step once; the models can then be used to make predictions or can be applied to new problems via transfer learning ⁴⁸, as discussed below.

Using these and other tools, protein language models are able to synthesize the enormous quantity of known protein sequences by training on 100s of millions of sequences stored in protein databases (e.g. UniProt, Pfam, NCBI ^15,49,50). The distribution over sequences learned by language models captures the evolutionary fitness landscape of known proteins. When trained on tens of thousands of evolutionarily related proteins, the learned probability mass function describing the empirical distribution over naturally occurring sequences has shown promise for predicting the fitness of sequence variants ^29-31. Because these models learn from evolutionary data directly, they are able to make accurate predictions about protein function when function is reflected in the fitness of natural sequences. Riesselman et al. first demonstrated that language models fit on individual protein families are surprisingly accurate predictors of variant fitness measured in deep mutational scanning datasets ²⁹. New work has since shown that the representations learned by language models are also powerful features for learning of variant fitness as a subsequent supervised learning task ^32,34, building on earlier observations that language models can improve protein property prediction through transfer learning ²⁷. Recently, Hie et al. used language models to learn evolutionary fitness of viral envelope proteins and were able to predict mutations that could allow the SARS-CoV-2 spike protein to escape neutralizing antibodies ^30,31. As of publication, several variants predicted to have high escape potential have appeared in SARS-CoV-2 sequencing efforts around the world, but viral escape has not yet been experimentally verified ⁵¹.

A few recent works have focused on increasing the scale of these models by adding more parameters and more learnable layers to improve sequence modeling. Interestingly, because so many sequences are available, these models continue to benefit from increased size ³². This parallels the general trend in natural language processing, where the number of parameters, rather than specific architectural choices, is the best indicator of model performance ⁵². However, ultimately, model size is limited by the computational resources available to train and apply these models. In NLP, models such as BERT and GPT-3 have become so large that only the best funded organizations with massive Graphics Processing Unit (GPU) compute clusters are realistically able to train and deploy them. This is demonstrated in some recent work on protein models where single transformer-based models were trained for days to weeks on hundreds of GPUs ^32,46,47, costing potentially 100s of thousands of dollars for training. Increasing the scale of these models promises to continue to improve our ability to model proteins, but more resource efficient algorithms are needed to make these models more accessible to the broader scientific community.

So far, the language models we have discussed use natural protein sequence information. However, they do not learn from the protein structure and function knowledge that has been accumulated over the past decades of protein research. Incorporating such knowledge requires supervised approaches.

Supervision encodes biological meaning

Proteins are more than sequences of characters: they are physical chains of amino acids that fold into three-dimensional structures and carry out functions based on those structures. The sequence-structure-function relationship is the central pillar of protein biology and significant time and effort has been spent to elucidate this relationship for select proteins of interest. In particular, the increasing throughput and ease-of-use of protein structure determination methods, (e.g. x-ray crystallography and cryo-EM ^53,54), has driven a rapid increase in the number of known protein structures available in databases such as the Protein Data Bank (PDB) ⁵⁵. There are nearly 175,000 entries in PDB as of publication and this number is growing rapidly. 14,000 new structures were deposited in 2020 and the rate of new structure deposition is increasing. We pursue the intuition that incorporating such knowledge into our models via supervised learning can aid in predicting function from sequence, bypassing the need for solved structures.

Supervised learning is the problem of finding a mathematical function to predict a target variable given some observed variables. In the case of proteins, supervised learning is commonly used to predict protein structure from sequence, protein function from sequence, or for other sequence annotation problems (e.g., signal peptide or transmembrane region annotation). Beyond making predictions, supervised learning can be used to encode specific semantics into learned representations. This is common in computer vision where, for example, pre-training image recognition models on the large ImageNet dataset is used to prime the model with information from natural image categories ⁵⁶.

When we use supervised approaches, we encode semantic priors into our models. These priors are important for learning relationships that are not obvious from the raw data. For example, unrelated protein sequences can form the same structural fold and, therefore, are semantically similar. However, we cannot deduce this relationship from sequences alone. Supervision is required to learn that these sequences belong to the same semantic category. Although structure is more informative of function than sequence ^57,58 and structure is encoded by sequence, predicting structure remains hard, particularly due to the relative paucity of structural relative to sequence data. Significant strides have been made recently with massive computing resources ²⁶; yet there is still a long way to go before a complete sequence to structure mapping is possible. The degree to which such a map could or should be possible, even in principle, is unclear.

Evolutionary relationships between sequences are informative of structural and functional relationships, but only when the degree of sequence homology is sufficiently high. Above 30% sequence identity, structure and function are usually conserved between natural proteins ⁵⁹. Often called the “twilight zone” of protein sequence homology, proteins with similar structures and functions still exist below this level, but they can no longer be detected from sequence similarity alone and it is unclear whether their functions are conserved. Although it is generally believed that proteins with similar sequences form similar structures, there are also interesting examples of highly similar protein sequences having radically different structures and functions ^60,61 and of sequences that can form multiple folds ⁶². Evolutionary innovation requires that protein function can change with only a few mutations. Furthermore, it is important to note that although structure and function are related, they should not be directly conflated.

These phenomena suggest that there are aspects of protein biology that may not be discoverable by statistical sequence models alone. Supervision that represents known protein structure, function, and other prior knowledge may be necessary to encode distant sequence relationships into learned embeddings. By analogy, cars and boats are both means of transportation, but we would not expect a generative image model to infer this relationship from still images alone. However, we can teach these relationships through supervision.

On this premise, we hypothesize that incorporating structural supervision when training protein language models will improve the ability to predict function in downstream tasks through transfer learning. Eventually, such language models may become powerful enough that we can predict function directly without the need for solved structures. In the remainder of this Synthesis, we will explore this idea.

Multi-task language models capture the semantic organization of proteins

Here, we will demonstrate that training protein language models with self-supervision on a large amount of natural sequence data and with structure supervision on a smaller set of sequence, structure pairs enriches the learned representations and translates into improvements in downstream prediction problems (Figure 3). First, we generate a dataset that contains 76 million protein sequences from Uniref ⁶³ and an additional 28,000 protein sequences with structures from the Structural Classification of Proteins (SCOP) database, which classifies protein sequences into a hierarchy of structural motifs based on their sequence and structural similarities (e.g. family, super-family, class) ^64,65. Next, we train a bidirectional LSTM with three learning tasks simultaneously: 1) the masked language modeling task (Figure 3a, 2c), 2) residue-residue contact prediction (Figure 3b), and 3) structural similarity prediction (Figure 3c).

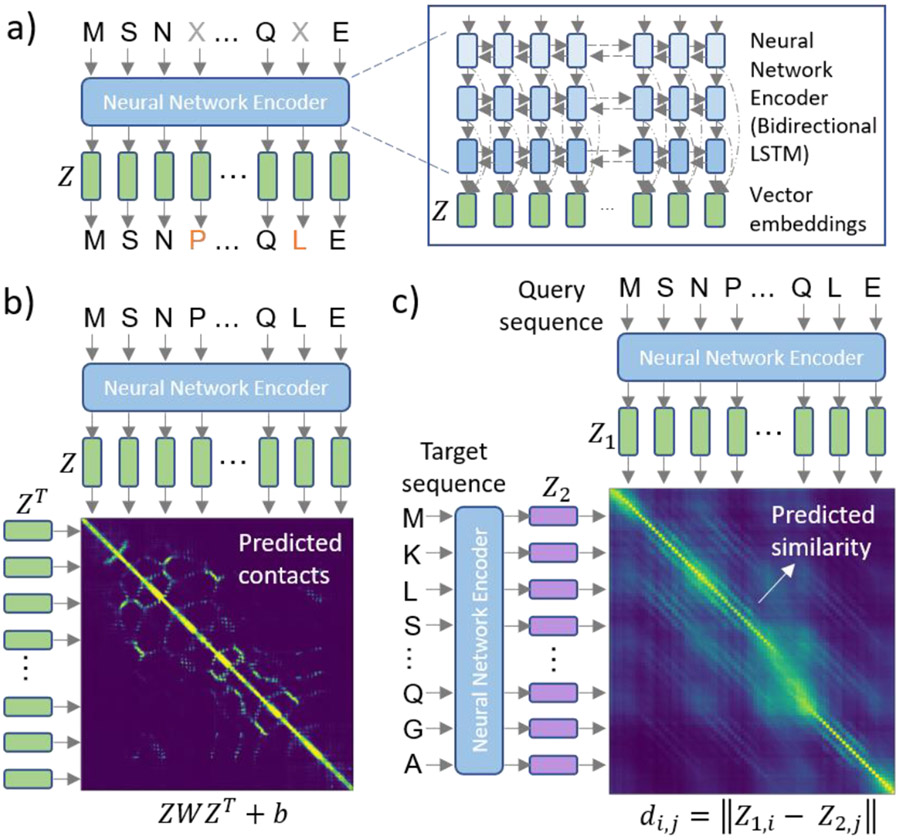
Figure 3 ∣.

Our multi-task contextual embedding model learning framework. We train a neural network (NN) sequence encoder to solve three tasks simultaneously. The first task is masked language modeling on millions of natural protein sequences. We include two sources of structural supervision in a multi-task framework (MT-LSTM for Multi-Task LSTM) in order to encode structural semantics directly into the representations learned by our language model. We combine this with the masked language model objective to benefit from evolutionary and less available structure information (only 10s of thousands of proteins). a) The masked language model objective allows us to learn contextual embeddings from hundreds of millions of sequences. Our training framework is agnostic to the NN architecture, but we specifically use a three-layer bidirectional LSTM with skip connections (inset box) in this work in order to capture long range dependencies but train quickly. We can train language models using only this objective (DLM-LSTM) but can also enrich the model with structural supervision. b) The first structure task is predicting contacts between residues in protein structures using a bilinear projection of the learned embeddings. In this task, the hidden layer representations of the language model are then used to predict residue-residue contacts using a bilinear projection. That is, we model the log likelihood ratio of a contact between the i-th and j-th residues in the protein sequence, by z_iWz_j + bwhere matrix W and scalar b are learned parameters. c) The second source of structural supervision is structural similarity, defined by the Structural Classification of Proteins (SCOP) hierarchy ¹²⁰. We predict the ordinal levels of similarity between pairs of proteins by aligning the sequences in embedding space. Here, we embed the query and target sequences using the language model (Z₁ and Z₂) and then predict the structural homology by calculating the pairwise distances between the query and target embeddings (d_i,j) and aligning the sequences based on these distances.

The fundamental idea behind this novel training scheme is to combine self-supervised and supervised learning approaches to overcome the shortcomings of each. Specifically, the masked language modeling objective (self-supervision) allows us to learn from millions of natural protein sequences from the Uniprot database. However, this does not include any prior semantic knowledge from protein structure and, therefore, has difficulty learning semantic similarity between divergent sequences. To address this, we consider two structural supervision tasks, residue-residue contact prediction and structural similarity prediction, trained with tens of thousands of protein structures classified by SCOP. In the residue-residue contact prediction task, we use the hidden layers of the language model to predict contacts between residues within the 3D structure using a learned bilinear projection layer (Figure 3b). In the structural similarity prediction task, we use the hidden layers of the language model to predict the number of shared structural levels in the SCOP hierarchy by aligning the proteins in vector embedding space and using this alignment score to predict structural similarity from the sequence embeddings. This task is critical for encoding structural relationships between unrelated sequences into the model. The parameters of the language model are shared across the self-supervised and two supervised tasks and the entire model is trained end-to-end. The set of proteins with known structure is much smaller than the full set of known proteins in Uniprot and, therefore, by combining these tasks in a multi-task learning approach we can learn language models and sequence representations that are enriched with strong biological priors from known protein structures. We refer to this model as the MT-(multi-task-)LSTM.

Next, we demonstrate how the trained language model can be used for protein sequence analysis and compare this with conventional approaches. Given the trained MT-LSTM, we apply it to new protein sequences to embed them into the learned semantic representation space (Figure 4a). Sequences are fed through the model and the hidden layer vectors are combined to form vector embeddings of each position of the sequences. Given a sequence of length L, this yields L D-dimensional vectors, where D is the dimension of the vector embeddings. This allows us to map the semantic space of each residue within a sequence, but we can also map the semantic space of whole sequences by summarizing them into fixed size vector embeddings via a reduction operation. Practically, this is useful for coarse sequence comparisons including clustering and manifold embedding for visualization of large protein datasets, revealing evolutionary, structural, and functional relationships between sequences in the dataset (Figure 4b). In this figure, we visualize proteins in the SCOP dataset, colored by structural class, after embedding with our MT-LSTM. For comparison, we also show results of embedding using a bidirectional LSTM trained only with the masked language modeling objective (DLM-LSTM), which is not enriched with the structure-based priors. We observe that even though the DLM-LSTM model was trained using only sequence information, protein sequences still organize roughly by structure in embedding space. However, this organization is improved when we include structure supervision in the language model training (Figure 4b).

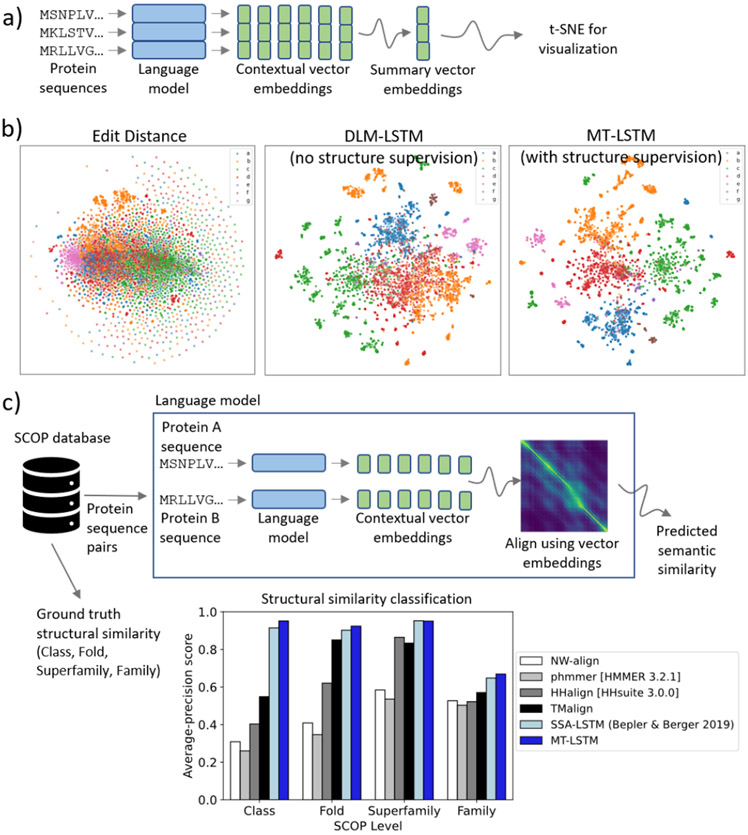
Figure 4 ∣.

Language models capture the semantic organization of proteins. a) Given a trained language model, we embed sequences by processing them with the neural network and taking the hidden layer representations for each position of the sequence. This gives an LxD matrix containing a D-dimensional vector embedding for each position of a length L sequence. We can reduce this to a D-dimensional vector “summarizing” the entire sequence by a pooling operation. Specifically, we use averaging here. These representations allow us to directly visualize large protein datasets with manifold embedding techniques. b) Manifold embedding of SCOP protein sequences reveals that our language models learn protein sequence representations that capture structural semantics of proteins. We embed thousands of protein sequences from the SCOP database and show t-SNE plots of the embedded proteins colored by SCOP structural class. The masked language (unsupervised) model (DLM-LSTM) learns embeddings that separate protein sequences by structural class, whereas the multi-task language model (MT-LSTM) with structural supervision learns an even better organized embedding space. In contrast, manifold embedding of sequences directly (edit distance) produces an unintelligible mash and does not resolve structural groupings of proteins. c) In order to quantitatively evaluate the quality of the learned semantic embeddings, we calculate the correspondence between semantic similarity predicted by our language model representations and ground truth structural similarities between proteins in the SCOP database. Given two proteins, we calculate the semantic similarity between them by embedding these proteins using our MT-LSTM, align the proteins using the embeddings, and calculate an alignment score. We compute the average-precision score for retrieving pairs of proteins similar at different structural levels in the SCOP hierarchy based on this predicted semantic similarity and find that our semantic similarity score dramatically outperforms other direct sequence comparison methods for predicting protein similarity. Furthermore, our entirely sequence-based method even outperforms structural comparison with TMalign when predicting structural similarity in the SCOP database. Furthermore, we contrast our end-to-end MT-LSTM model with an earlier two-step language model (SSA-LSTM) and find that training end-to-end in a unified multi-task framework improves structural similarity classification.

The semantic organization of our learned embedding space enables a direct application: we can search protein sequence databases for semantically related proteins by comparing proteins based on their vector embeddings ²⁷. Because we embed sequences into a semantic representation space, we can find structurally related proteins even though their sequences are not closely related (Figure 4c, Supplemental Table 1). To demonstrate this, we take pairs of proteins in the SCOP database, not seen by our multi-task model during training, and calculate the similarity between these pairs of sequences using direct sequence homology-based methods (Needleman-Wunsch alignment, HMM-sequence alignment, and HMM-HMM alignment^66-68), a popular structure-based method (TMalign ⁶⁹), and an alignment between the sequences in our learned embedding space. We then evaluate these methods based on their ability to correctly find pairs of proteins that are similar at the class, fold, superfamily, and family level, based on their SCOP classification. We find that our learned semantic embeddings dramatically outperform the sequence comparison methods and even outperform structure comparison with TMalign when predicting structural similarity. Interestingly, we observe that the structural supervision component is critical for learning well organized embeddings at a fine-grained level, because the DLM-LSTM representations alone do not perform well at this task (Supplemental Table 1). Furthermore, the multi-task learning approach outperforms a two-step learning approach presented previously (SSA-LSTM)²⁷.

With the success of our self-supervised and supervised language models, we sought to investigate whether protein language models could improve function prediction through transfer learning.

Transfer learning improves downstream applications

A key challenge in biology is that many problems are small data problems. Quantitative protein characterization assays are rarely high throughput and methods are needed that can generalize given only 10s to 100s of experimental measurements. Furthermore, we are often interested in extrapolating from data collected over a small region of protein sequence space to other sequences, often with little to no homology. Learned protein representations improve predictive ability for downstream prediction problems through transfer learning (Figure 5a). Transfer learning is the problem of applying knowledge learned from solving some prior tasks to a different task of interest. In other words, learning to solve task A can help learn to solve task B; analogously, learning how to wax cars helps to learn karate moves (Karate Kid, 1984). This is especially useful for tasks with little available training data, such as protein function prediction, because models can be pre-trained on other tasks with plentiful training data to improve performance through transfer learning.

Figure 5 ∣.

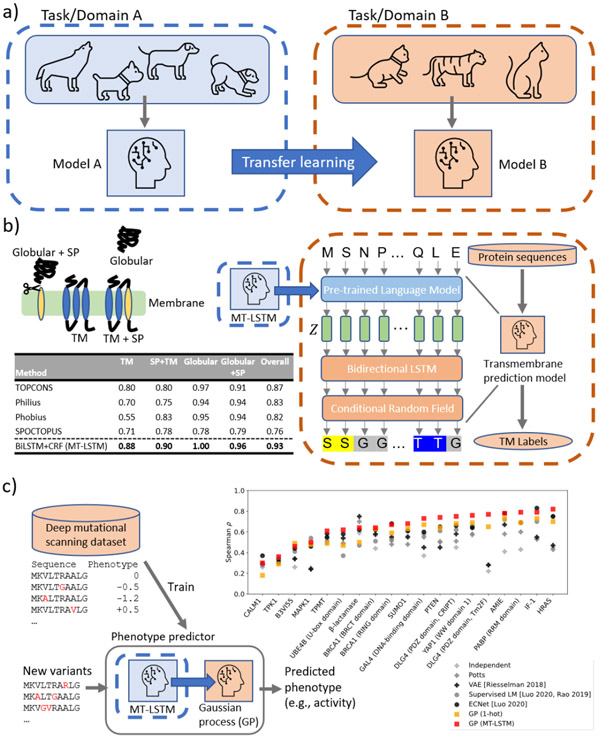
Protein language models with transfer learning improve function prediction. a) Transfer learning is the problem of applying knowledge gained from learning to solve some task, A, to another related task, B. For example, applying knowledge from recognizing dogs to recognizing cats. Usually, transfer learning is used to improve performance on tasks with little available data by transferring knowledge from other tasks with large amounts of available data. In the case of proteins, we are interested in applying knowledge from evolutionary sequence modeling and structure modeling to protein function prediction tasks. b) Transfer learning improves transmembrane prediction. Our transmembrane prediction model consists of two components. First, the protein sequence is embedded using our pre-trained language model (MT-LSTM) by taking the hidden layers of the language model at each position. Then, these representations are fed into a small single layer bidirectional LSTM (BiLSTM) and the output of this is fed into a conditional random field (CRF) to predict the transmembrane label at each position. We evaluate the model by 10-fold cross validation on proteins split into four categories: transmembrane only (TM), signal peptide and transmembrane (TM+SP), globular only (Globular), and globular with signal peptide (Globular+SP). A protein is considered correctly predicted if 1) the presence or absence of signal peptide is correctly predicted and 2) the number of locations of transmembrane regions is correctly predicted. The table reports the fraction of correctly predicted proteins in each category for our model (BiLSTM+CRF) and widely used transmembrane prediction methods. A BiLSTM+CRF model trained using 1-hot embeddings of the protein sequence instead of our language model representations performs poorly, highlighting the importance of transfer learning for this task (Supplemental Table 2). c) Transfer learning improves sequence-to-phenotype prediction. Deep mutational scanning measures function for thousands of protein sequence variants. We consider 19 mutational scanning datasets spanning a variety of proteins and phenotypes. For each dataset, we learn the sequence-to-phenotype mapping by fitting a Gaussian process regression model on top of representations given by our pre-trained language model. We compare three unsupervised approaches (+), prior works in supervised learning (∘), and our Gaussian process regression approaches with (□, GP (MT-LSTM)) and without (GP (1-hot)) transfer learning by 5-fold cross validation. Spearman rank correlation coefficients between predicted and ground truth functional measurements are plotted. Our GP with transfer learning outperforms all other methods, having an average correlation of 0.65 across datasets. The benefits of transfer learning are highlighted by the improvement over the 1-hot representations which only reach 0.57 average correlation across datasets. Transfer learning improves performance on 18 out of 19 datasets.

Application of protein language models to downstream tasks through transfer learning was first demonstrated by Bepler & Berger ²⁷. They showed that transfer learning was useful for structural similarity prediction, secondary structure prediction, residue-residue contact prediction, and transmembrane region prediction, by fitting task specific models on top of a pre-trained bidirectional language model. The key insight was that the sequence representations (vector embeddings) learned by the language model were powerful features for solving other prediction problems. Since then, various language model-based protein embedding methods have been applied to these and other protein prediction problems through transfer learning, including protein phenotype prediction ^28,32-34, residue-residue contact prediction ^32,70, fold recognition ³³, protein-protein ^71,72 and protein-drug interaction prediction ^35,73. Recent works have shown that increasing language model scale leads to continued improvements in downstream applications, such as residue-residue contact prediction ⁷⁰. We also find that increasing model size improves transfer learning performance.

Here, we demonstrate two use cases where transfer learning from our MT-LSTM improves performance on downstream tasks. First, we consider the problem of transmembrane prediction. This is a sequence labeling task in which we are provided with the amino acid sequence of a protein and wish to decode, for each position of the protein, whether that position is in a transmembrane (i.e., membrane spanning) region of the protein or not. This problem is complicated by the presence of signal peptides, which are often confused as transmembrane regions.

In order to compare different sequence representations for this problem, we train a small one-layer bidirectional LSTM with a conditional random field (BiLSTM+CRF) decoder on a well-defined transmembrane protein benchmark dataset⁷⁴. Methods are compared by 10-fold cross validation. We find that the BiLSTM+CRFs with our new embeddings (DLM-LSTM and MT-LSTM) outperform existing transmembrane predictors and a BiLSTM+CRF using our previous smaller embedding model (SSA-LSTM). Furthermore, representations learned by our MT-LSTM model significantly outperform (paired t-test, p=0.044) the embeddings learned by our DLM-LSTM model on this application (Figure 5b).

Second, we demonstrate that we can accurately predict functional implications of small changes in protein sequence through transfer learning. An ideal model would be sensitive down to the single amino acid level and would group mutations with similar functional outcomes closely in semantic space. Recently, Luo et al. presented a method for combining language model-based representations with local evolutionary context-based representations (ECNet) and demonstrated that these representations were powerful for sequence-to-phenotype mapping on a panel of deep mutational scanning datasets ³⁴. In this problem, we observe a relatively small set (100s-1000s) of sequence-phenotype measurement pairs and our goal is to predict phenotypes for unmeasured variants. Observing that these are small data problems, we reasoned that this is an ideal setting for Bayesian methods and that transfer learning will be important for achieving good performance. To this end, we propose a framework in which sequence variants are first embedded using our MT-LSTM and then phenotype predictions are made using Gaussian process (GP) regression using our embeddings as features. We find that we can predict the phenotypes of unobserved sequence variants across datasets better than existing methods (Figure 5c). Our MT-LSTM embedding powered GP achieves an average Spearman correlation of 0.65 with the measured phenotypes significantly outperforming (paired t-test, p=0.006) the next best method, ECNet, which reaches 0.60 average Spearman correlation.

Semi-supervised learning ⁷⁵, few-shot learning ⁷⁶, meta-learning ^77,78, and other methods for rapid adaptation to new problems and domains will be key future developments for pushing the limit of data efficient learning. Methods that capture uncertainty (e.g., Gaussian processes and other Bayesian methods) will continue to be important, particularly for guiding experimental design. Some recent works have explored Gaussian process-based methods for guiding protein design with simple protein sequence representations ^79-81. Hie et al, presented a GP-based method for guiding experimental drug design informed by deep protein embeddings ³⁵. Other works have explored combining neural network and GP models ^82,83 while still others considered non-GP-based uncertainty aware prediction methods for antibody design and major histocompatibility complex (MHC) peptide display prediction ^84,85. Methods for combining multiple predictors and for incorporating strong priors into protein design can also help to alleviate problems that arise in the low data regime ⁸⁶. Transfer learning and massive protein language models will play a key role in future protein property prediction and machine learning driven protein and drug design efforts.

Conclusions and Perspectives: Strong biological priors are key to improving protein language models

Future developments in protein language modeling and representation learning will need to model properties that are unique to proteins. Biological sequences are not natural language, and we should develop new language models that capture the fundamental nature of biological sequences. While demonstrably useful, existing methods based on recurrent neural networks and Transformers still do not fundamentally encode key protein properties in the model architecture and the inductive biases of these models are only roughly understood (Box 1).

Box 1 ∣.

Inductive bias describes the assumptions that a model uses to make predictions for data points it has not seen ¹¹⁷. That is, the inductive bias of a model is how that model generalizes to new data. Every machine learning model has inductive biases, implicitly or explicitly. For example, protein phenotype prediction based on homology assumes that phenotypes covary over evolutionary relatedness. In other words, it formally models the idea that proteins that are more evolutionarily related are likely to share the same function. In thinking about deep neural networks applied to proteins, it is important to understand the inductive biases these models assume, because it naturally relates to the true properties of the function we are trying to model. However, this is challenging, because we can only roughly describe the inductive biases of these models ¹¹⁸.

Proteins are objects that exist in physical space. Similarly, we understand many of the fundamental evolutionary processes that give rise to the diversity of protein sequences observed today. These two elements, physics and evolution, are the key properties of proteins and our models might benefit from being structured explicitly to incorporate evolutionary and physics-based inductive biases. Early attempts at capturing physical properties of proteins as part of machine learning models have already demonstrated that conditioning on structure improves generative models of sequence³⁶ and significant work has been done in the opposite direction of machine learning-based structure prediction methods that explicitly incorporate constraints on protein geometries ^3,5,26,87-89. However, new methods are needed to fuse these directions with physics-based approaches and to start to fully merge sequence- and structure-based models.

At the same time, current protein language models make heavily simplified phylogenetic assumptions. By treating each sequence as an independent draw from some prior distribution over sequences, current methods assume that all protein sequences arise independently in a star phylogeny. Conventionally, this problem is crudely addressed by filtering sequences based on percent identity. However, significant effort has been dedicated to understanding protein sequences as emerging from tree-structured evolutionary processes over time or coalescent processes in reverse time ^90,91. Methods for inferring these latent phylogenetic trees continue to be of substantial interest ^92-94, but are frustrated by long run times and poor scalability to large datasets. In the future, deep generative models of proteins might seek to merge these disciplines to model proteins as being generated from evolutionary processes other than star phylogenies.

Other practical considerations continue to frustrate our ability to develop new protein language models and rapidly iterate on experiments. High compute costs and murky design guidelines mean that developing new models is often an expensive, time consuming, and ad hoc process. It is not clear at what dataset sizes and levels of sequence diversity one model will outperform another or how many parameters a model should include. At the upper limit of large natural protein databases, larger models continue to yield improved performance. However, for individual protein families or other application specific protein data sets, the gold standard is to select model architectures and number of parameters via brute force hyperparameter search methods. Fine-tuning pre-trained models can help with this problem but does not fully resolve it. Sequence length also remains a challenge for these models. Transformers scale quadratically with sequence length, which means that in practical implementations long sequences need to either be excluded or truncated. New linear complexity attention mechanisms may help to alleviate this limitation ^95,96. This problem is less extreme for recurrent neural networks, which scale linearly with sequence length, but very long sequences are still impractical for RNNs to handle and long-range sequence dependencies are unlikely to be learned well by these models.

Language models capture complex relationships between residues in protein sequences by condensing information from enormous protein sequence databases. They are a powerful new development for understanding and making predictions about biological sequences. Increasing model size, compute power, and dataset size will only continue to improve performance of protein language models. Already, these methods are transforming computational protein biology today due to their ease of use and widespread applicability. Furthermore, augmenting language models with protein specific properties such as structure and function offers one already successful route towards even richer representations and novel biology. However, it remains unclear how best to encode prior biological knowledge into the inductive bias of these models. We hope this Synthesis propels the community to work towards developing purpose-built protein language models with natural inductive biases suited for the physical nature of proteins and how they evolve.

Methods

Bidirectional LSTM encoder with skip connections

We structure the sequence encoder of our DLM- and MT-LSTM models as a three-layered bidirectional LSTM with skip connections from each layer to the final output. Our LSTMs have 1024 hidden units in each direction of each layer. We feed a 1-hot encoding of the amino acid sequence as the input to the first layer. Given a sequence input, x, of length L, this sequence is 1-hot encoded into a matrix, O, of size Lx21 where entry o_i,j = 1 if x_i=j (that is, amino acid x_i has index j) and o_i,j = 0 otherwise. We then calculate H⁽¹⁾ = f⁽¹⁾(O), H⁽²⁾ = f⁽²⁾(H⁽¹⁾), H⁽³⁾ = f⁽³⁾(H⁽²⁾), and Z = [H⁽¹⁾ H⁽²⁾ H⁽³⁾] where H^(a) is the hidden units of the ath layer and f^(a) is ath BiLSTM layer. The final output of the encoder, Z, is the concatenation of the hidden units of each layer along the embedding dimension.

Masked language modeling module

We use a masked language modeling objective for training on sequences only. During training, we randomly replace 10% of the amino acids in a sequence with either an auxiliary mask token or a uniformly random draw from the amino acids and train our model to predict the original amino acids at those positions. Given an input sequence, x, we randomly mask this sequence to create a new sequence, x’. This sequence is fed into our encoder to give a sequence of vector representations, Z. We decode these vectors into a distribution over amino acids at each position, p, using a linear layer. The parameters of this layer are learned jointly with the parameters of the encoder network. We calculate the masked language modeling loss as the negative log likelihood of the true amino acid at each of the masked positions, L_masked = $-\frac{1}{n}{\sum }_i\log p_i{,}_{x_i}$ where there are n masked positions indexed by i.

Residue-residue contact prediction module

We predict intra-residue contacts using a bilinear projection of the sequence embeddings. Given a sequence, x, with embeddings, Z, calculated using our encoder network, the bilinear projection calculates ZWZ^⊤ + b, where W and b are learnable parameters of dimension DxD and 1 respectively where D is the dimension of an embedding vector. These parameters are fit together with the parameters of the encoder network. This produces an LxL matrix, where L is the length of x. We interpret the i,jth entry in this matrix as the log-likelihood ratio between the probability that the ith and jth residues are within 8 angstroms in the 3D protein structure and the probability that they are not. We then calculate the contact loss, L_contact, as the negative log-likelihood of the true contacts given the predict contact probabilities.

Structure similarity prediction module

Our structure similarity prediction module follows previously described methods ²¹. Given two input sequences, X and X’ with lengths N and M, that have been encoded into vector representations, Z and Z’, we calculate reduced dimension projections, A = ZB and A’ = Z’B, where B is a DxK matrix that is trained together with the encoder network parameters. K is a hyperparameter and is set to 100. Given A and A’, we calculate the inter-residue semantic distances between the two sequences as the manhattan distance between embedding at position i in the first sequence and embedding at position j in the second sequence, d_i,j = ∥A_i - A’_j∥₁. Given these distances, we calculate a soft alignment between the positions of sequences X and X’. The alignment weight between two positions, i and j, is defined as c_i,j = α_i,j + β_i,j − α_i,jβ_i,jwhere ${\alpha }_{i,j}=\frac{k_{i,j}}{{\sum }_{l=1}^N{k}_{i,l}}$ and ${\beta }_{i,j}=\frac{k_{i,j}}{{\sum }_{l=1}^M{k}_{l,j}}$ and $k_{i,j}=e^{-d_{i,j}}$. With the inter-residue semantic distances and the alignment weights, we then define a global similarity between the two sequences as the negative semantic distance between the positions averaged over the alignment, $s=-\frac{1}{C}{\sum }_{i,j}{c}_{i,j}{d}_{i,j}$ where c = Σ_i,jc_i,j.

With this global similarity based on the sequence embeddings in hand, we need to compare it against a ground truth similarity in order to calculate the gradient of our loss signal and update the parameters. Because we want our semantic similarity to reflect structural similarity, we retrieve ground truth labels, t, from the SCOP database by assigning increasing levels of similarity to proteins based on the number of levels in the SCOP hierarchy that they share. In other words, we assign a ground truth label of 0 to proteins not in the same class, 1 to proteins in the same class but not the same fold, 2 to proteins in the same fold but not the same superfamily, 3 to proteins in the same superfamily but not in the same family, and finally 4 to proteins in the same family. We relate our semantic similarity to these levels of structural similarity through ordinal regression. We calculate the probability that two sequences are similar at a level t or higher as p(y ≥ t) = θ_ts + b_t where θ_t and b_t are additional learnable parameters for t ≥ 1. We impose the constraint that θ_t ≥ 0 to ensure that increasing similarity between the embeddings corresponds to increasing numbers of shared levels in the SCOP hierarchy. Given these distributions, we calculate the probability that two proteins are similar at exactly level t as p(y = t) = p(y ≥ t)(1 − p(y ≥ t + 1)). That is, the probability that two sequences are similar at exactly level t is equal to the probability they are similar at at least level t times the probability they are not similar at a level above t.

We then define the structural similarity prediction loss to be the negative log-likelihood of the observed similarity labels under this model, L_similarity = −log p(y = t).

Multi-task loss

We define the combined multi-task loss as a weighted sum of the language modeling, contact prediction, and similarity prediction losses, L_MT = λ_maskedL_masked + λ_contactL_contact + λ_similarityL_similarity.

Training datasets

We train our masked language models on a large corpus of protein sequences, UniRef90⁶³, retrieved in July 2018. This dataset contains 76,215,872 protein sequences filtered to 90% sequence identity. For structural supervision, we use the SCOPe ASTRAL protein dataset previously presented by Bepler & Berger^27,64,65. This dataset contains 28,010 protein sequences with known structures and SCOP classifications from the SCOPe ASTRAL 2.06 release. These sequences are split into 22,408 training sequences and 5,602 testing sequences.

Hyperparameters and training details

We train two language models with different settings of the weights in the loss term. The first model, DLM-LSTM, uses only the masked language modeling objective so is trained with λ_masked = 1, λ_contact = 0, and λ_similarity = 0. The second model, MT-LSTM, uses the full multi-task objective with weights λ_masked = 0.5, λ_contact = 0.9, and λ_similarity = 0.1. The DLM-LSTM model was trained for 1,000,000 parameter updates using a minibatch size of 100 using the Adam optimizer⁹⁷ with a learning rate of 0.0001. The MT-LSTM model was also trained for 1,000,000 parameter updates using Adam with a learning rate of 0.0001, but, due to GPU RAM restrictions, we had to train the MT-LSTM model with smaller minibatch sizes of 64 for the masked language model objective and 16 for the structure-based objectives. Following Bepler & Berger²⁷, we sampled pairs of proteins for the structural similarity prediction task with an exponential smoothing parameter, τ = 0.5, to oversample the relatively rare highly similar protein pairs in the dataset. During training, we applied a mild regularization on the structure tasks by randomly resampling positions from a uniform distribution over amino acids with probability 0.05.

Models were implemented using PyTorch ⁹⁸ and trained on a single NVIDIA V100 GPU with 32GB of RAM. Training time was roughly 13 days for the DLM-LSTM model and 51 days for the MT-LSTM model.

Protein structural similarity prediction evaluation

We evaluate protein structural similarity methods on the SCOPe ASTRAL test set described above (Training datasets). All methods are evaluated on 100,000 randomly sampled protein pairs in this dataset. For each prediction method, we calculate the predicted similarity between each pair using only the sequence of each protein with the exception of TMalign which operates on the protein structures. Because TMscore is not symmetric, we calculate TMscore for both comparison directions and average them together for each protein pair. We found this outperformed other methods of combining the two scores. For HHalign, we first constructed profile HMMs for each protein by iteratively searching for homologues in the uniprot30 database provided by the authors using HHblits ⁹⁹. We then calculate the similarities between each pair of proteins by aligning their HMMs with HHalign. For protein language model embedding methods, we calculate the predicted similarity as described above (Structural similarity prediction module).

We compare the predicted structural similarity scores against the ground truth scores defined by SCOP across a variety of metrics. Accuracy is the fraction of protein pairs for which the similarity level is predicted exactly correctly. We also calculate the Pearson correlation coefficient (r) and Spearman rank correlation coefficient (ρ) between the predicted and ground truth similarities. Finally, we calculate the average-precision score for retrieving pairs of proteins at or above each level of similarity. That is, we report the average-precision score for each method where the positive set is proteins in the same class, in the same fold, in the same superfamily, or in the same family.

Transmembrane region prediction training and evaluation

We follow the procedure for transmembrane prediction and evaluation previously described by Tsirigos et al and the model described by Bepler & Berger ^27,74. The TOPCONS2 dataset contains protein sequences and transmembrane annotations for four categories of proteins: 1) proteins with transmembrane regions (TM), 2) proteins with transmembrane regions and a signal peptide (TM+SP), 3) proteins without transmembrane regions or a signal peptide (globular), and 4) proteins without transmembrane regions but with a signal peptide (globular+SP). Altogether, the dataset contains 5154 proteins broken down into 286 TM, 627 TM+SP, 2927 globular, and 1314 globular+SP proteins.

In order to compare different protein representations for transmembrane prediction, we fit a single layer BiLSTM followed by a conditional random field (CRF) decoder using either 1-hot encodings of the amino acid sequence or embeddings generated by the SSA-LSTM, DLM-LSTM, or MT-LSTM models. The BiLSTM has 150 hidden units in each direction and the CRF decodes the outputs of the BiLSTM to one of four states: signal peptide, cytosolic region, transmembrane region, or extracellular region. In the CRF, we use the hidden state grammar and transitions defined by Tsirigos et al. ¹⁰⁰ and only fit the input potentials. The models are trained for 10 epochs over the data with a batch size of 1 using the Adam optimizer⁹⁷ with a learning rate of 0.0003.

We compare methods by 10-fold cross validation. We calculate prediction performance over proteins in the held-out set by decoding the most likely sequence of labels using the Viterbi algorithm and then scoring a protein as correctly predicted if 1) the protein is globular and we predict no transmembrane or signal peptide regions, 2) the protein is globular+SP and we predict that the protein starts with a signal peptide and has no transmembrane regions, 3) the protein is TM and we predict the correct number of transmembrane regions with at least 50% overlap to the ground truth regions and no signal peptide, and 4) the protein is TM+SP is the same as TM except that we also predict that the protein starts with a signal peptide.

Sequence-to-phenotype prediction and evaluation

We retrieve the set of deep mutational scanning datasets aggregated by Riesselman et al ²⁹ and follow the supervised learning procedure used by Luo et al ³⁴. These datasets contain phenotypic measurements of sequence variants across a variety of proteins and measured phenotypes. Phenotypes include enzyme function ^101,102, growth ^103-108, stability ¹⁰⁹, peptide binding ^110,111, ligase activity ¹¹², and MIC ¹¹³.

For each dataset, we featurize the amino acid sequences of each variant as either a 1-hot encoding or by embedding the sequence with our MT-LSTM model. We then apply dimensionality reduction to these vectors using PCA down to the minimum of 1000 PCs or the number of data points in the dataset to improve the runtime of the learning algorithm. We then fit a Gaussian process (GP) regression model using the RBF kernel and fit the kernel hyperparameters by maximum likelihood. We implement our GP models in GPyTorch ¹¹⁴. To compare methods, we follow Luo et al and perform 5-fold cross validation on each deep mutational scanning dataset ³⁴ and calculate the Spearman rank correlation coefficient between our predicted phenotypes and the ground truth phenotypes on the heldout data for each fold.

Glossary

1-hot [embedding].

Vector representation of a discrete variable commonly used for discrete values that have no meaningful ordering. Each token is transformed into a V-dimensional zero vector, where V is the size of the vocabulary (the number of unique tokens, e.g., 20, 21, or 26 for amino acids depending on inclusion of missing and non-canonical amino acid tokens), except for the index representing the token, which is set to one.

autoregressive [language model].

Language models that factorize the probability of a sequence into a product of conditional probabilities in which the probability of each token is conditioned on the preceding tokens, $p(x_1\dots x_L)={\prod }_{i=1}^{L}p(x_i\mid x_1\dots x_{i-1})$. Examples of autoregressive language models include k-mer (AKA n-gram) models, Hidden Markov Models, and typical autoregressive recurrent neural network or generative transformer language models. These models are called autoregressive because they model the probability of one token after another in order.

Bayesian methods.

A statistical inference approach that uses Bayes rule to infer a posterior distribution over model parameters given by the observed data. Because these methods describe distributions over parameters or functions, they are especially useful in small data regimes or other settings when prediction uncertainties are desirable.

cloze task.

A task in natural language processing, also known as the cloze test. The task is to fill in missing words given the context. For example, “The quick brown ____ jumps over the lazy dog.”

conditional random field.

Models the probability of a set (sequence in this case, i.e. linear chain CRF) of labels given a set of input variables by factorizing it into locally conditioned potentials conditioned on the input variables, $p(y_1\dots y_L\mid x_1\dots x_L)=p(y_1\mid x_1\dots x_L){\prod }_{i=2}^{L}p(y_i\mid y_{i-1},x_1\dots x_L)$. This is often simplified such that each conditional only depends on the local input variable, i.e., $p(y_1\dots y_L\mid x_1\dots x_L)=p(y_1\mid x_1){\prod }_{i=2}^{L}p(y_i\mid y_{i-1},x_i)$. Linear chain CRFs can be seen as the discriminative version of Hidden Markov Models.

contextual vector embedding.

Vector embeddings that include information about the sequence context in which a token occurs. Encoding context into vector embeddings is important in NLP, because words can have different meanings in different contexts (i.e., many homonyms exist). For example, in the sentences, “she tied the ribbon into a bow” and “she drew back the string on her bow,” the word bow refers to two different objects that can only be inferred from context. In the case of proteins, this problem is even worse, because there are only 20 (canonical) amino acids and so their “meaning” is highly context dependent. This is in contrast to typical vector embedding methods that learn a single vector embedding per token regardless of context.

distributional hypothesis.

The observation that words that occur in similar contexts tend to have similar meanings. Applies also to proteins due to evolutionary pressure¹¹⁵.

Gaussian process.

A class of models that describes distributions over functions conditioned on observations from those functions. Gaussian processes model outputs as being jointly normally distributed where the covariance between the outputs is a function of the input features. See Rasmussen and Williams for a comprehensive overview ¹¹⁶

generative model.

A model of the data distribution, p(X), joint data distribution, p(X, Y), or conditional data distribution, p(X∣Y = y). Usually framed in contrast to discriminative models that model the probability of the target given an observation, p(Y∣X = x). Here, Xis observable, for example the protein sequence, and Yis a target that is not observed, for example the protein structure or function. Conditional generative and discriminative models are related by Bayes’ theorem. Language models are generative models.

hidden layer.

Intermediate vector representations in a deep neural network. Deep neural networks are structured as layered data transformations before outputting a final prediction. The intermediate layers are referred to as “hidden” layers.

inductive bias.

Describes the assumptions that a model uses to make predictions for data points it has not seen ¹¹⁷. That is, the inductive bias of a model is how that model generalizes to new data. Every machine learning model has inductive biases, implicitly or explicitly. For example, protein phenotype prediction based on homology assumes that phenotypes covary over evolutionary relatedness. In other words, it formally models the idea that proteins that are more evolutionarily related are likely to share the same function. In thinking about deep neural networks applied to proteins, it is important to understand the inductive biases these models assume, because it naturally relates to the true properties of the function we are trying to model. However, this is challenging, because we can only roughly describe the inductive biases of these models ¹¹⁸.

language model.

Probabilistic model of whole sequences. In the case of natural language, language models typically describe the probability of sentences or documents. In the case of proteins, they model the probability of amino acid sequences. Being simply probabilistic models, language models can take on many specific incarnations from column frequencies in multiple sequence alignments to Hidden Markov Models to Potts models to deep neural networks.

manifold embedding.

A distance preserving, low dimensional embedding of the data. The goal of manifold embedding is to find points low dimensional vectors, z₁ … z_n, such that the distances, d(z_i, z_j), are as close as possible to the distances in the original data space, d(x_i, x_j), given n high dimensional data vectors, x₁…x_n. t-SNE is a commonly used manifold embedding approach for visualization of high dimensional data.

masked language model.

The training task used by BERT and other recent bidirectional language models. Instead of modeling the probability of a sequence autoregressively, masked language models seek to model the probability of each token given all other tokens. For computational convenience, this is achieved by randomly masking some percentage of the tokens in each minibatch and training the model to recover those tokens. An auxiliary token is added to the vocabulary to indicate that this token has been masked.

multi-task learning.

A machine learning paradigm in which multiple tasks are learned simultaneously. The idea is that similarities between tasks can lead to each task being learned better in combination rather than learning each individually. In the case of representation learning, multi-task learning can also be useful for learning representations that encode information relevant for all tasks. Multi-task learning allows us to use the signals encoded in other training signals as an inductive bias when learning the goal task.

representation learning.

The problem of learning features, or intermediate data representations, better suited for solving a prediction problem on raw data. Deep learning systems are described as representation learning systems, because they learn a series of data transformations that make the goal task progressively easier to solve before outputting a prediction.

residue-residue contact prediction.

The task of learning which amino acid residues are in contact in folded protein structures, where contact is assumed to be within a small number of angstroms, often with the goal of constraining the search space for protein structure prediction.

self-supervised learning.

A relatively new term for methods for learning from data without labels. Generally used to describe methods that “automatically” create labels through data augmentation or generative modeling. Can be viewed as a subset of unsupervised learning focused on learning representations useful for transfer learning.

semantic priors.

Prior semantic understanding of a word or token, e.g., protein structure or function.

semantics.

The meaning of a word or token. In reference to proteins, we use semantics to mean the “functional” purpose of a residue, or combinations of residues.

structural classification of proteins (SCOP).

A mostly manual curation of structural domains based on similarities of their sequences and structure. Similar databases include CATH ¹¹⁹.

structural similarity prediction.

Given two protein sequences, predict how similar their respective structures would be according to some similarity measure.

supervised learning.

A problem in machine learning. How we can learn a function to predict a target variable, usually denoted y, given an observed one, usually denoted x, from a set of known x, y pairs.

transfer learning.

A problem in machine learning. How we can take knowledge learned from one task and apply it to solve another related task. When the tasks are different but related, representations learned on one task can be applied to the other. For example, representations learned from recognizing dogs could be transferred to recognizing cats. In the case of proteins and language models, we are interested in applying knowledge gained from learning to generate sequences to predicting function. Transfer learning could also be applied to applying representations learned from predicting structure to function or from predicting one function to another function among other applications.

unsupervised learning.

A problem in machine learning that asks how we can learn patterns from unlabeled data. Clustering is a classic unsupervised learning problem. Unsupervised learning is often formulated as a generative modeling problem, where we view the data as being generated from some unobserved latent variable(s) that we infer jointly with the parameters of the model.

vector embedding.

A term used to describe multidimensional real numbered representations of data that is usually discrete or high dimensional, word embeddings being a classic example. Sometimes referred to as “distributed vector embeddings” or “manifold embeddings” or simply just “embeddings.” Low-dimensional vector representations of high dimensional data such as images or gene expression vectors as found by methods such as t-SNE are also vector embeddings. Usually, the goal in learning vector embeddings is to capture some semantic similarity between data as a function of similarity or distance in the vector embedding space.