ALEKS constructs as predictors of high school mathematics achievement for struggling students

Abstract

The purpose of this study was to determine what factors of the Assessment and Learning in Knowledge Spaces (ALEKS), an ITS, are predictive of struggling learners’ performance in a blended-learning Algebra 1 course at an inner city technical high school located in the northeastern U.S. Three variables (student retention, engagement time, and the ratio of topics mastered to topics practiced) were used to predict the degree of association on the criterion variable (mathematics competencies), as measured by final course progress grades in algebra, and the Preliminary Scholastic Assessment Test (PSATm) math scores. A correlational predictive design was applied to assess the data of a purposive sample of 265 struggling students at the study site; multiple regression analysis was also used to investigate the predictability of these variables. Findings suggest that engagement time and the ratio of mastered to practiced topics were significant predictors of final course progress grades. Nevertheless, these factors were not significant contributors in predicting PSATm score. Retention was identified as the only statistically significant predictor of PSATm score. The results offer educators with additional insights that can facilitate improvements in mathematical content knowledge and promote higher graduation rates for struggling learners in high school mathematics.

Highlights

• •Introduction addresses intelligent tutoring systems in blended learning settings to assist teaching and learning practices.
• •Focus on ALEKS intelligent tutoring system, learning achievement, and classroom dynamics.
• •Includes the analysis of 265 data logs in a predictive correlational design.
• •Main conclusion is that engagement time and the ratio of mastered to practiced topics were predictors of course grades.
• •Additional conclusion is that retention was identified as the only statistically significant predictor of PSATm score.
• •Main challenges were gathering and organizing the data.

Distance education and online learning; Secondary education.

1. Introduction

Educationalists view mathematics as one of the most difficult subjects to master in education, and many individuals across the United States demonstrate challenges with attaining proficiency in mathematics concepts and skills. U.S. high school graduates are among these nonproficient math learners, with many requiring remediation in higher education, according to Johnson and Samora (2016). The rapid infusion of intelligent tutoring systems (ITS) in high school mathematics courses has provided educators with unprecedented opportunities to engage learners in active learning (Dani, 2016; Fine et al., 2009; Icoz et al., 2015; Liu, Rogers and Pardo, 2015b) and potentially address nonproficiency issues. Such online learning platforms aid teachers with assessing, instructing, monitoring, modifying, and differentiating instruction to address the diverse needs of students.

Nonetheless, many learners at risk of failing high school mathematics continue to experience difficulties in such milieus (Gasevic et al., 2016; McManis and McManis, 2016). Their lack of self-management and self-regulation skills exacerbates the challenges these students face in these settings. It is therefore imperative that stakeholders are aware of effective supports that influence the achievement of struggling learners in these learning platforms. Accordingly, the purpose of this study is to determine the predictability of the constructs of a commonly used ITS program known as the Assessment and Learning in Knowledge Spaces (ALEKS) on struggling students' achievement in a high school Algebra 1 course and to determine what ITS program variables are the best predictors to support these learners' success in this arena. Such findings may inform effective interventions to maximize struggling learners’ performance in similar learning environments now and in the future.

1.1. Background

Technological advancements have contributed to the increased application of computer-based instruction and adaptive tutors to aid the success of learners in the United States. Of these systems, intelligent tutors have been the most frequently applied in recent years (Kulik and Fletcher, 2016). These tutoring and assessment systems are capable of identifying and gauging individualized learning. Elnajjar and Naser (2017) asserted that adaptive techniques affiliated with ITS shows promise in supporting the learning of students in blended settings (a combination of in-person and e-learning methods). These systems incorporate cognitive theories along with artificial intelligence to infer students’ knowledge (Johnson and Samora, 2016; Kulik and Fletcher, 2016) as well as make intelligent decision to coach them toward improved learning. Educationalists incorporated these programs in blended-learning settings to determine what students know and to motivate and engage them in rigorous activities that would enhance their performance outcomes.

Educators incorporate ITSs in blended settings to assist the teaching and learning processes, promote diversification, and to foster andragogic practices for learning. Such application provides educationalists with encouraging outlooks for the use of one-to-one learning devices (Johnson and Samora, 2016) to facilitate independent learning and differentiated instruction. Accordingly, a growing number of learners are being exposed to ITSs on a yearly basis (Chen and Yao, 2016). These students are required to demonstrate self-management and self-regulation skills to facilitate their progress in these settings. Nonetheless, the blended-learning arena has provided instructors with challenges in managing and promoting struggling learners. The heuristics that educators require to assess students' disengagement are not readily available or easily transferable in the online platform (Liu et al., 2015a). Still, the recent fields of education data mining (EDM) and learning analytics (LA) have optimized the potential for improved knowledge and understanding of such behaviors. Through advancements in these fields, practitioners are able to measure and analyzed large amounts of students behavioral data from ITS databases to garner greater insights related to students' who are at risk for failure in these online modalities, and to develop and apply modifications to improve their performance in these settings (Gasevic et al., 2016; Holstein et al., 2017; Icoz et al., 2015; Liu et al., 2015a, 2015b; San Pedro, 2017). Accordingly, educators view these new developments in teaching and learning models as a panacea for despondent results (Johnson and Samora, 2016) in struggling students’ mathematical achievement across the United States.

However, few researchers have conducted studies to assess the effect of ITS adaptive instruction on high school students' mathematics achievement or identify ITS variables that are most effective at predicting these learners’ success in blended-learning mathematics courses at the secondary level. A few of these investigations suggest a need for further evaluation of ITS and various system factors (including time on ITS content information) that might improve the effectiveness of the individualized teaching and learning processes (Dani, 2016; Icoz et al., 2015; San Pedro, 2017).

1.2. ALEKS

The ALEKS web-based program is an ITS that is designed to apply mathematical instruction and ongoing assessments to monitor and manage students' knowledge acquisition. Similar to other ITSs, the computer platform gathers data related to learners' working behavior pattern and provides appropriate feedback and guidance to support their learning needs (Dani, 2016). Educationalists can obtain and apply this data to differentiate instruction to address the needs of students. The program provides learners with (1) individualized sequence of problems to solve, (2) implements knowledge checks to assess their understanding (implemented continuously and at the end of course goals), and (3) guidance via instructional practice review to promote learning and understanding of problem-solving skills (McGraw-Hills, 2017). Nonetheless, ALEKS provides the same level of instruction to all students irrespective of their diverse learning styles and provides instructors with the opportunity to upload external video presentations to assist students’ visual and auditory learning demands (Dani and Nasser, 2016).

The ALEKS software program uses a curriculum-based approach (Johnson and Samora, 2016) which minimizes adjustments to school districts' curriculum practices. Hence, educators can apply ALEKS in blended settings to deliver an entire mathematics curriculum via individualized instruction (McGraw Hill Education, 2017b); and apply problems that are within the learners Zone of Proximal Development (ZPD) to facilitate the knowledge, skills, and behavior that promotes conceptual understanding (Dani and Nasser, 2016) and mathematical thinking. Similar to most ITSs for numeracy, program developers created ALEKS to address the current problems relevant to students' mathematical achievement. Educators at the postsecondary level of instruction apply this ITS to improve the remediation problems associated with learning mathematics (Johnson and Samora, 2016) and to promote competency-based education at the K-12 level of education. However, unlike other ITSs that provides procedural step-by-step guidance when completing a problem, ALEKS only provide feedback on the final answer (Dani, 2016; Dani and Nasser, 2016). Dani (2016) asserted that the inability for students to demonstrate strategies for problem-solving within the ALEKS program may limit the software's capability to measure meta-cognition for learning.

The body of research on the effectiveness of the ALEKS software program is limited. Most of these investigations center on the impact of ALEKS on students' math achievements at the postsecondary level. Nonetheless, recent studies have been growing at the secondary levels of instruction and results have been mixed. Several of these studies show promising effects related to the ALEKS ITS on struggling students’ math achievement.

For example, a pilot study was instituted by Hu et al. (2012) to investigate the effectiveness of the ALEKS ITS on improving the mathematical skills of struggling sixth-grade students in an after-school setting. The participants included 266 sixth-grade students and four math instructors who were randomly assigned to an ALEKS centered or a teacher-centered condition. The researchers applied a state standardized assessment to measure student performance outcomes, and a t-test analysis and multiple regression evaluations to analyze pre- and post-standardized test scores and ALEKS data logs. The results indicated no significant differences between pre- and post-standardized test scores. However, the regression examination predicted 29% of the observed variance for students' post-standardized test scores. These findings revealed that higher post-test scores were predicted by participants’ pre-test scores, attendance, and gender; while experimental treatment and race reported insignificant results.

Brasiel et al. (2016) conducted a mixed method study with the use of a quasi-experimental and survey design to assess the impact of 11 computer-assisted instruction (CAI) mathematical software programs on student achievement gains. The exploration included 200,000 K-12 students who participated in the quasi-experimental method and 2,933 instructors who completed survey responses. This study was the first assessment of a 2-year impact inquiry. A state standardized assessment was applied as a measure of student achievement performance. The authors used a baseline comparison and logistic regression analysis to analyze quantitative data and a thematic approach was instituted to assess survey responses. The investigators identified six products that met the established criteria to conduct an impact analysis and two modalities (ALEKS and iReady) that demonstrate statistically significant achievement variations (p < .05). Further results indicated that teachers were satisfied with the technologies ability to manage performance assessments and engage and empower students in learning activities. Nonetheless, obstacles related to teacher attitude and experience with technology, and infrastructure relevant to these platforms, were noted by the researchers.

Sullins et al. (2013) applied an examination to determine if individualized instruction in the ALEKS ITS will increase students' performance on a state standardized assessment. The researchers solicited middle school students (from grades 6, 7, and 8) who participate in a supplemental application of the ALEKS ITS during the academic year. The authors conducted two studies. The objective of the first study was to identify if mastery of ALEKS goal topics correlated with success on the Tennessee Comprehensive Assessment Program, a state standardized assessment. The second study replicated and expands on the findings from the first study and included a new sample from a different district. A total of 218 students from two school districts participated in the first study. The practitioners instituted a correlation analysis to compare the percentage of students' mastered topics in ALEKS with achievement scores. The results indicated a positive and statistically significant relationship between both scores at each grade level. Specifically, the researchers identified a significant positive correlation between the ALEKS mathematical categories measure and learners’ standardized mathematics category measures (including Numbers and Operations, Algebraic Thinking, Graphs and Graphing, Data Analysis and Processing, Measurement, and Geometry).

The second study that was carried out by Sullins et al. (2013) assessed the relationship across and within grade levels. This examination involved 321 middle school students (from grades 5, 6, and 7) and included those measures applied in the first study. The results confirmed the findings of study 1 and revealed a positive statistically significant correlation between and within these scores. The authors suggest that students’ proficiency in ALEKS can be a potential predictor of future performance on the Tennessee Comprehensive Assessment measure. The researchers did caution these results based on the lack of rigorous analysis and methodology within the research.

A more recent study that was carried out by Brasiel et al. (2016) used a mixed-method study to evaluate the effectiveness of 11 online mathematics educational technology products on the achievements of 200,000 K-12 students during the 2014-15 academic year. The practitioners applied a quasi-experimental design and a qualitative self-reported survey to address the research questions. The participants were separated into a technology group (with one-to-one application) and a traditional instructional (business-as-usual) group. The results from the logistic regression analysis of 44, 497 students favored the use of the technological products, and the ALEKS ITS was identified as one of the programs that demonstrated a statistically significant positive impact on struggling students' achievement. The survey data were obtained from 2, 933 teachers and a thematic approach was incorporated to identify commonalities. Teachers overall response to the use of the technology in the classroom was positive. The findings indicated that 57% of the teachers were satisfied with the software products and 10% were satisfied with their students' engagement when using these modalities. However, only 34% of the instructors reported using the performance management features within the products to monitor students’ progress. The authors reflected disappointment at the small percentage of responders who applied the management feature to support students and guide instruction as this was one of the primary function of the mathematical platforms.

In contrast to the above findings, some researchers postulate that ALEKS provides minimal to no advantage to learning in traditional classrooms. Craig et al. (2013) reported insignificant finding in their experimental study that assessed the effectiveness of the ALEKS ITS on improving the mathematical skills of struggling middle school students. A sample of sixth-grade individuals was recruited to participate in a 25-week afterschool program. The participants included 253 sixth-graders from a large disadvantaged minority population and five teachers that were randomly chosen from a group of 25 instructors. The students were randomly assigned to a teacher-centered and an ALEKS centered classroom in an after-school setting. The authors applied a state examination to measure students’ performance outcomes. Teachers were also asked to rate students conduct, involvement, and need for assistance, based on a three-point scale ranging from poor to excellent (not involved to actively involved) and a 2-point scale reflecting no help to more help than usual. A t-test analysis was conducted on all scores, and no significant difference was observed between struggling students who participate in the ALEKS after-school tutoring program and those who did not. However, students in the ALEKS-led condition required significantly less assistance in mathematics from teachers than their counterparts (ALEKS-led: M = 0.05, SD = 0.11; and Teacher-led: M = 0.65, SD = 0.27).

In a similar study involving ALEKS at the secondary level, Huang et al. (2016) conducted an experimental evaluation of 533 sixth-grade students (from five middle schools) to explore the effects of ALEKS on mathematics achievement. The research question for this study addressed the mathematics performance gap in education and the prospects of ITSs towards reducing this gap. The investigation focused on data from the last 2-years of a 3-year study that placed students in an after-school setting. The participants were randomly assigned to an ALEKS ITS led and a teacher-led condition. The researchers conducted a t-test analysis and observed no significant difference in scores between the two conditions (even though scores favored the ALEKS ITS condition). Nonetheless, the authors reported encouraging results for the application of ALEKS to aid the education of struggling youth. The practitioners concluded that White males and females, and African American males and females performed differently on the math state test in the teacher-led condition; and students who had varied individual differences demonstrated similar performances in the ALEKS ITS setting.

Most of the above studies were implemented at the middle school level of instruction. Few investigators have assessed the influences of the ALEKS ITS on struggling students' mathematics performances at the high school level of instruction, and that may identify program construct that may act as predictors for students’ success. A possible explanation for such limitations may be the constraints associated with the ability to conduct large data analysis. However, recent developments in the field of large data have opened up numerous possibilities of such investigations.

1.2.1. Data mining and learning analytics

Computer tutoring supports the diversification of instruction to facilitate teaching and learning processes in and outside the classroom, provides timely feedback to students and flexible learning plans, and offers managerial assistance for synchronous and asynchronous educational processes (Chappell et al., 2015). Such personalization is bolstered by the emerging field of large data analysis. This field facilitates the use of EDM and LA to optimize understanding of student learning patterns and behaviors in various CAI learning environments, and to support the identification of learning problems linked to the timely signs of students at risk for academic failure and attrition (Gasevic et al., 2016). According to Henrie et al. (2015), technology records summative and formative data on students' system interactions and can provide pertinent data on their engagement in learning. The behavior and progress data can be recorded directly through these modalities (Hu et al., 2017). Gasevic et al. (2016) posit that “the interpretation of these patterns can be used to improve our understanding of learning and teaching processes, predict the achievement of learning outcomes, and inform support interventions and decisions on resources allocation” (p. 68). Most research in EDM and LA has coalesced around predicting the achievement and retention of students at risk of failing particular CAI courses; and to identify common variables that individually or collectively inform a general model (Gasevic et al., 2016). Nonetheless, the literature on this body of research is limited, and studies are commonly applied at the postsecondary level to assess the impact of ITSs on students’ academic success. Some studies have been employed at the secondary level; however, these studies largely involve other ITS modalities (similar to ALEKS).

For example, a correlational study of Bringula et al. (2016) assessed the relationship between high school students' prior mathematical knowledge on time spent tutoring, total hints requested, and the number of completed quizzes in a SimStudent ITS program. The participants were involved in 1-hour SimStudent sessions over a 3-day intervention period. These respondents included 139 (of 236) first-year high school students who were enrolled in the Introductory Algebra course, and who completed both the test examinations and the three-day intervention period. The authors applied two measures for this investigation. The evaluation included three Introductory Algebra pre- and post-test that were used to gain an understanding of students' knowledge (as related to linear equations), and data logs related to students' interaction were collected from the SimStudent (i.e., time spent tutoring, number of hints requested by the program, and number of quizzes conducted) were correlated. Results indicated that 11 % of the variability in the time spent tutoring, 5% of the variability in the number of quizzes conducted, and 3% of the variability in the number of hints requested were due to students’ prior mathematical knowledge. The authors concluded that prior knowledge demonstrated a significant, consistent, positive influence on learner-interface interactions (i.e., time spent tutoring, number of hints requested by the program, and number of quizzes conducted) with the ITS program. Nonetheless, recommendations were made to extend the intervention period for future studies.

Zacharis (2015) assessed data generated in the data logs of a computer management system (Moodle) to determine a realistic model for predicting struggling students' performance in blended-learning mathematics courses. The author sought to determine the relationship between students' final course grades and their interaction in online modalities. The practitioner accumulated 29 potential explanatory variables and identified 14 variables with significant association to students' course grades. These variables were selected for application in a stepwise multivariate regression analysis. The participants of the study included 134 college students who were enrolled in an introductory Java programming course that was instituted over a 12-week period. The research findings indicated that reading and posting message (37.6%), content creation contribution (10.4%), quiz effort (2.5%), and the number of files viewed (1.5%) predicted 52% of the variance in student final course grade. Reading and posting messages contributed the greatest variance (37.6%) in students’ scores.

Dani and Nasser (2016) conducted a study of ALEKS at the higher education level to determine potential identifiers of students' academic success in foundational mathematics. The participants included a sample of 152 college students who were divided into three clusters (numbered one – three) based on derived attributes. Students in cluster one demonstrated the highest ratio of weekly topics mastered to topics practiced (averaging 80%). Leaners in cluster three symbolized the lowest values (averaging 53%) within this variable (cluster average percentages represented 80%, 66%, and 53%). The research measures involved students' activity data from the ALEKS data logs. The ALEKS factors included learners' score on initial assessments, the ratio of weekly topics mastered to topics practiced, number of progress test (knowledge assessments), final exam score, and whether students completed the course before the 12-week period or not. A Chi-square, ANOVA test, and Regression analysis were employed to address the research questions. Results indicated that student ratio of topics mastered to practiced was predictive of students' academic success in the course. This component represented a significant moderately strong, positive correlation with student final exam marks. The authors indicated that the ratio of topics mastered to topics practices represented 16% of the variance in students' final exam scores. Further results indicated that learners’ English language proficiency affected their ability to learn independently.

Dani (2016) implemented a quantitative investigation at the postsecondary level to determine potential identifiers (within ALEKS) of students' academic success. This study sought to expand on findings from the previous study carried out by Dani and Nasser (2016). The respondents included 58 students who were enrolled in a foundational mathematics course over a 12-week period. The researchers implemented a cross-sectional design to triangulate the measures of students’ ALEKS data logs and survey responses. The study implemented Chi-square, correlational and regression analysis, and pair t-test to address the research questions. The findings suggest that learners prior knowledge and derived attitude (a ratio of topics mastered to topics practiced) were predictive of final course marks (R² = 42%). Further results indicated that students who selected topics sequentially demonstrated better retention of mathematical content than students who progress randomly through topics. These findings afford instructors the opportunity to monitor the progress of struggling students who are unable to maintain proper pacing and provide guidance in the selection of appropriate (sequential) topics.

The use of the ALEKS ITS in blended-learning settings affords educators the opportunity to customized instruction to address the individual needs of learners. Nonetheless, the body of research that explores what factors of ITSs that are best predictors of struggling students' performance is limited. Although studies exist at the postsecondary level that addresses ALEKS factors (ratio of topics mastered to topics practiced) to be predictive of students' mathematics success, very limited research investigations have been conducted at the secondary level. The findings from this study are expected to contribute to this knowledge base by investigating factors of the ALEKS ITS online software that are predictive of struggling students’ mathematics competency. Such insights can facilitate greater success for learners who are at risk for failure in these milieus, improve mathematical content knowledge, promote higher graduation rates, and increased job opportunities.

Accordingly, the following broad research questions were addressed:

• RQ1: Is engagement time, retention, and the ratio of topics mastered to topics practiced (in ALEKS) for students identified as at risk for failure in mathematics predictive of final Algebra 1 course progress grades?



• RQ2: Is engagement time, retention, and the ratio of topics mastered to topics practiced (in ALEKS) for students identified as at risk for failure in mathematics predictive of PSAT math scores?

The following alternative hypotheses were tested:

• H_a1: Engagement time, retention, and the ratio of topics mastered to topics practiced (in ALEK) will be significant predictors of final Algebra 1 course progress grades, α ≤ 0.05.



• H_a2: Engagement time, retention, and the ratio of topics mastered to topics practiced (in ALEK) will be significant predictors of PSAT math scores, α ≤ 0.05.

The null hypotheses were the following:

• H₀1: Engagement time, retention, and the ratio of topics mastered to topics practiced (in ALEK) will not be significant predictors of final Algebra 1 course progress grades, α ≤ 0.05.



• H₀2: Engagement time, retention, and the ratio of topics mastered to topics practiced (in ALEK) will not be significant predictors of PSAT math scores, α ≤ 0.05.

1.3. Theoretical foundations

The theoretical foundations for this investigation included the knowledge space theory (KST), the ZPD, and the cognitive learning theory (CLT) which are combined to assist the instruction and learning process in blended-learning platforms.

1.3.1. Knowledge space theory

The knowledge space theory stems from the mathematical cognitive sciences behind ALEKS (McGraw-Hill Education, 2017a). The origin of this theoretical framework encompasses the work of Jean-Paul Doignon and Jean-Claude Falmagne whose goal was to improve the psychometric approach to assessing individual competencies (Doignon and Falmagne, 2015). These theorists described the KST as the collection of all possible state of knowledge that exists within the mathematical domain (Craig et al., 2013). A few researchers (Craig et al., 2013), stated that this theory incorporates the compilation of various sets of problems as related to mathematical concepts and problem-solving skills, and facts. Accordingly, Doignon and Falmagne's ideas on the KST underscore the diagnosis of students' math competencies (state of knowledge) based on their mastery of particular items on adaptive knowledge assessments that are comprised of 25–30 problem types (McGraw-Hills, 2017). Craig et al. (2013) suggested that the program can identify what information students already know and can apply; what they are ready to do; and what they are unable to accomplish and adjust problem types based on the analysis of all collected information. Thomas and Gilbert (2016) asserted that this adaptive ability of ITSs is underpinned by the theoretical foundations of the (ZPD) and the Cognitive Learning Theory (CLT).

1.3.2. Zone of Proximal Development

Vygotsky (1978) introduced the idea of the ZPD and identified student’ intellectual development has not only what learners can do, but also what they can do with assistance. By fostering the acquisition of the learners' ZPD, educators can apply ITS scaffolding methods to support learning processes to align new learning with what students already know and can do, and concentrate lessons around what students are prepared to learn with guidance. Through these practices, educators can minimize learning anxiety by ensuring that appropriate tasks are presented with attention to students' background knowledge (Chounta et al., 2017). Instructors can use the program to construct and identify new knowledge based on the explorations and discoveries of what students are ready to learn. Accordingly, educationalists can incorporate ITSs to guide and consultant students’ academic learning.

1.3.3. Cognitive learning theory

Various theologians contributed to the cognitive principles. A few of these theorists include Thorndike, Lindeman, Rogers, Maslow, and Dewey's conceptualization of scientific thinking (Knowles et al., 2005). The principle of cognitive theory places the learner's mental inquiry at the center of learning, according to Knowles et al. (2005). These researchers stated that learners' mental inquiries are influenced by intrinsic and extrinsic experiences and the student's surrounding environment. Knowles et al. (2005) aligned this theory with student-centered learning environments, as opposed to conventional education where instruction is teacher-centered and students are required to conform to the pedagogic processes. The students garner educational acumen to achieve personal objectives. Leaners demonstrate this understanding in the practices associated with adult learning (andragogy) where learning is directly influenced by the students and their experiences. Hawkins et al. (2017) stated that through the acquisition of these background experiences, learners are able to maximize their self-actualization and the ability to be a self-directed learner. The latter promotes the personalization of new information by stimulating a deep sense of value and meaning that facilitates personal growth (Hawkins et al., 2017). Learners apply this awareness to cultivate a greater connectedness to new topics and to drive motivation for furthering one's education. Hence, educators can incorporate personalized learning to promote reflection between learning and experiences and facilitate active interaction to assess the trials and errors of new knowledge. Program developers and educators apply these insights to underscore the development and implementation of one-to-one adaptive learning with the use of adaptive ITS programs.

Educationalists combine and apply the three philosophies in blended-settings to optimize their abilities to differentiate instruction and effectively address the needs of learners. Based on these theories, one would predict that students who are provided with instruction at a level geared to them would make considerable advances in mathematics achievement and would demonstrate the acquisition of the current mathematical standards as they relate to 21st-century skills.

1.4. Sample and setting

The sample for this study centered primarily on a purposive sample of 265 ninth- and 10th-grade high school students at an urban technical high school in a low socioeconomic community in the northeast United States. Creswell (2012) asserted that purposive sampling is frequently applied in educational research because random selection and random assignment to interventions are rarely possible in these settings. Approximately 530,000 students from this state were enrolled in K-12 learning institutions at the time of this investigation, and an estimated 31,000 individuals represented the selected population that was germane to this investigation. The guidance coordinator at the study location stated that 585 of the individuals from this site were represented in the selected population. The sampled 265 participants worked in the ALEKS ITS program during the 2015–2016 and 2016–2017 academic year, the first 2 years of implementation. The author of this research solicited individuals who participated in the ITS software, achieved a final progress grade for the course, and participated in the PSAT in the Fall of their sophomore year. Individuals who were expelled, transferred in or out of the program, or missing values relevant to this investigation during this time frame were eliminated from the dataset. The data reports of the participants reflected the first and second year the intervention was implemented in their ninth-grade Algebra 1 course (the 2015–2016 and 2016–2017 academic years). Students in other cohorts and from other locations did not participate in this research. Including such participants in the study may pose possible threats to external validity (see Creswell, 2012).

The sample was very diverse in their experience, background knowledge, and ability level and according to the guidance counselor, at the site, a large percentage of learners were at least one to three grade levels behind in their math learning. The researcher did not interact with participants and instead applied student archival data reports as the central analytical focus for this investigation. As a result, due to the nature of this predictive study, there was no need to obtain participant consent to conduct this investigation.

All ninth-grade students had been placed in (one of three) Algebra 1 blended-learning mastery-based math classes where one-to-one devices had been implemented and the ALEKS ITS software program incorporated as the predominant form of instruction. The course groups were organized and predetermined by the district and school leaders at the study's location. The classrooms were assembled in a stationary format where students worked in collaborative groups when learning in the program before reporting to testing stations that were allotted for knowledge assessments and district mathematics evaluations. Students worked in the online program for the entire instructional period (approximately 1 hour each school day) and also had the opportunity to work in the program outside of school hours as well. In this environment, teachers acted as facilitators to assist students as needed and to apply the ALEKS managerial tools to monitor students who may need additional support.

Upon logging into the ALEKS interface, students are offered an initial assessment that evaluates the learner's state of knowledge. Once this initial step is accomplished, each subsequent log-in directs students to their pie chart that reflects their learning progress towards achieving their course completion (refer to Figure 1 for visual display). A student can choose to work towards gaining new topics or to review topics already learned (Dani and Nasser, 2016). Each slice of the ALEKS pie chart depicts a different set of mathematics objectives that replicates the learner's knowledge state depending on what he or she understands and is ready to learn (McGraw Hill Education, 2047b). The program sequentially delivers math topics; however, students can also choose to work on any ready-to-learn topics within a given domain group (i.e., goal topics; Dani and Nasser, 2016). Once presented with a topic, students can request an explanation to support their learning or proceed to solve the problem on their own. In addition to the latter, instructors required all students to write notes to facilitate their learning needs.

Figure 1.

ALEKS pie chart depicting learners' status and course content.

Students are recognized in the program as having learned a topic after three (to five) consecutive correct responses to a problem type. According to Dani (2016), these processes allow students to work at their own pace and monitor their learning. Instructors assign students a knowledge assessment once they have learned 10 or more topics. Nonetheless, ALEKS also assigns a progress assessment base on topics mastered and time spent in the software (Dani and Nasser, 2016). Accordingly, students are provided with progress assessments after completion of approximately 20–25 topics, and 10 hours of login time (McGraw Hill Education, 2047b). Learners may gain or lose topics in their pie chart based on their performances on provided progress assessments. These working behaviors are logged and tracked in the ALEKS database and can be applied to assess students’ learning within the online program (Dani and Nasser, 2016).

The investigator assumed that mathematics teachers at this location applied the ALEKS mastery-based curriculum effectively in the classrooms and students were actively engaged in the ITS during class time. In addition, the author also assumed that selected participants were fully versed in the use of the ALEKS ITS program in and outside of active learning in the math course. However, threats to internal validity existed as engagement time in the ALEKS ITS was recorded as the total time a student is logged into the program irrespective of their active or inactive performances. For example, a student can make no attempt to learn or master topics while logged into the program and will accrue idle time that is collected in the student's overall engagement time total (Dani, 2016). The accumulation and combination of these time differential in ALEKS may have impeded the validity of findings germane to student learning. Additionally, the students' ability to work in the program outside of school hours might compromise findings as some students might obtain assistance from their parents or older siblings during these timeframes. The latter delineates some students attaining more assistance than others. Such activities could have threatened the accuracy of the ALEKS measures.

2. Method and material

A correlational predictive design was implemented to evaluated the influence of the predictor variables (student engagement time, retention, and the ratio of topics mastered to topics practiced) on struggling students' performance as it pertains to the development of academic competency in mathematics (the criterion variable). The archival data were the focus of statistical analysis for this study. The author obtained the data from the ALEKS ITS data logs and the guidance department at the site of this investigation. The gathered reports reflected the mathematics achievement and learning behavior of learners from one high school institution. As previously stated, the participant groups were organized and predetermined by the organization; and the ALEKS ITS intervention was a district implemented intervention for the school beginning in the Fall of 2015. Because the intervention was introduced and completed before the collection of data, the researcher for this investigation was not required to solicit informed consent from participants (National Institute of Health, NIH; Office of Extramural Research, n. d.). Nevertheless, the author did obtain permission from the school district superintendent and the school principal for accessing and collecting archived statistics for this investigation; and once this study's IRB approval number (03-26-18-0317860) was received, the author commenced with collecting, organizing, and analyzing the data. Accordingly, the extracted data were printed and compiled in Microsoft Excel for further analysis in the SPSS software program.

The data were de-identified and linked to designated numbers that excluded the names of participants. Three predictor (independent) variables from the ALEKS data logs (retention, engagement time, and the ratio of topics mastered to topic practiced) and two criterion (dependent) variables (students' final Algebra 1 progress grades and PSAT math performance scores) were included in the analysis. Lodico et al. (2010) asserted that a predictive correlational methodology affords the opportunity to predict the linear relationship between two or more variables after the intervention period. By using this design, the author was able to investigate the collective and individual association between the three identified factors on mathematics competencies as defined by the ALEKS ITS online program theories and measured by the ALEKS data logs. A multiple regression analysis was applied to test the hypotheses. The correlation coefficient (r) and z-scores (R²) were utilized to determine the significance of engagement time, retention, and the ratio of topics mastered to topics practiced on students’ performance on final Algebra 1 course grades and/or PSAT scores. The following delineates the data sources and descriptions of the scale for each variable.

Engagement Time (depicted as ET in data tables) is a predictor variable that was extracted from the ALEKS database. This continuous variable reflects the combined (active and inactive) time logged in the program and is recorded in hours and minutes each time an individual logs in and out of the ITS during instructional (during school) and non-instructional (outside of school) periods. Accordingly, the author compiled the active and inactive time for participants and used these time attributes to explain student engagement within the context of this study. Hence, a quantitative estimate of engagement time was arrived at by combining students’ total log-in times in AKEKS from August 2015 to June 2016, and August 2016 to June 2017. These averages were recorded as the total amount of hours participants spent in the Algebra 1 class during the designated time period for this study. These recorded hours ranged from 0 to 500.

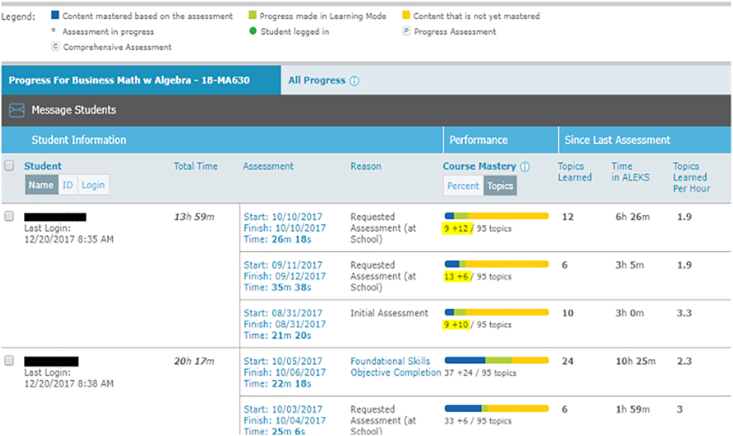
Retention (depicted as ren in the data tables) is a continuous predictor variable that was acquired from the ALEKS database. Unlike the ET construct, retention cannot be obtained directly from the software program. Nevertheless, the ALEKS program recognizes student's mastery of learned topics after they have demonstrated their competency of learned objectives on a knowledge assessment. The software records when students initiate a knowledge assessment and tracks students' progress between each assessment. Students' mastery of topics can fluctuate in gains and losses on progress between each knowledge assessment. The author of this study collected these scores and calculated the average percentages in mastered and learned topics. A comparison between participants mastered and learned topics can be used to assess the average percentage retention scores for individual learners and detect students who may require additional supports. For example, Figure 2 depicts a student that mastered nine topics on their initial knowledge assessment, then learned ten more during ALEKS instruction and achieved a total of 13 topics on their subsequent knowledge test. The latter represents 40% of students' retention in learning. Accordingly, this researcher collected these retention percentage scores and an average estimate was established for each student. Hence, this continuous variable ranges from 0 to 100, with higher scores denoting students' increased retention in learning.

Figure 2.

ALEKS progress report depicting a learner's retention after knowledge assessments.

The Ratio of Topics Mastered to Topics Practiced (mtop) is a continuous predictor variable that was obtained from two factors within the ALEKS program (mastered and practiced topics). This continuous variable is an attribute that was applied by Dani and Nasser (2016) to define the learning patterns of students who worked in the ALEKS ITS platform. Dani and Nasser (2016), and Dani (2016), stated that this variable represents an abbreviation of mastered to practiced topics and denotes the measure of students ability to learn independently. These authors stated that a higher ratio of this variable indicates increased capabilities to learn independently. Accordingly, this researcher applied this approach to calculate this attribute for this investigation. The participants total mastered and practiced topics were extracted for their respective years in the ALEKS Algebra 1 course (from August 2015 to June 2016, and August 2016 to June 2017). The combined totals were recorded as total topics mastered (ttm) and total topics practiced (ttp) in the data tables. The quotient of students' ttm to ttp were evaluated to establish a ratio of students’ mastered to practiced topics. This variable ranges from 0 to 1 in the data tables with higher ratios reflecting increase rates of mastered to practiced topics.

The PSAT, which was a continuous criterion variable in the study, is a standardized aptitude test that is administered by the College Board to assess the general intelligence of students in Grades 9 and 10 (Warne, 2016). It is also known as the National Merit Scholarship Qualifying Test (NMSQT). The measure may also predict students' performance on the SAT (Thum and Matta, 2015). According to Richardson et al. (2016), the PSAT exam is a condensed form of the SAT that provides students with feedback on current achievement skills. The exam tests learners' mathematics reasoning, critical reading, and writing skills (Richardson et al., 2016; Warne, 2016), and is a strong indicator of students' performance on the SAT (College Board, 2017a). The mathematics section of the PSAT measures a student's conceptual understanding and reasoning skills in numeracy (College Board, 2017a). This section includes topic objectives that are relevant to Algebra 1 and Geometry courses. The College Board (2017b) asserts that a mathematic grade-level benchmark score of 480 (indicating students who are performing at or above grade level) is established to track students' yearly progress towards attaining the SAT benchmark.

The sectional scores for the PSAT/NMSQT have a correlation that is greater than 0.80 with scores on the SAT and other measures of intelligence (Warne, 2016), and are directly related to math scores on the SAT College Board (2017c). For example, participants who completed the PSAT and the SAT on the same day would reflect the same score on both assessments. To ensure the validity and reliability of the SAT suite assessments (including the PSATs) the College Board frequently reviews student performance metrics and employs research-based designs to consistently evaluate test forms, prompts, questions, and items types (College Board, 2017d). A few researchers (Richardson et al., 2016) applied a multiple regression analysis to assess the predictive ability of portions of the PSAT on student advance placement performance and discovered a strong predictability between portions of the PSAT and students advance placement performance irrespective of ethnicity and socioeconomic status. Another researcher (Warne, 2016) established a conservative indicator of 0.84 as an internal reliability coefficient for each subtest of the PSAT. The author's findings also support the consistency of PSAT scores across test variations under similar conditions.

Students' Final Progress Grades (SFPG) is a continuous criterion variable that was ascertained from the school's guidance department. As stated previously, educators can apply the ALEKS platform in learning environments to monitor students' logged time and learning behavior patterns, and provide progress assessments based on their working behavior and time spent in the program (Dani and Nasser, 2016). According to researchers Falmagne et al., 2007, the program provides valid and reliable data pertaining to students' academic performance in mathematics. The mathematics teachers at the study site can apply this information to monitor students' progress and differentiate instruction to promote personalized learning, and to track final course progress grades. Math instructors at the location of this investigation, required learners to write notes when working in the ALEKS ITS, complete a minimum of 7–10 topic and 7–10 hours per week, and to complete the ALEKS districts goal assessments with a 70% minimum score. These teachers coalesced the scores for these requirements into one final percent average that reflected the students final progress grades for the course. The latter was used to denote the students final progress grades that ranged from 0 to 100 with higher scores reflecting increased progress with learning. According to the mathematics department chair at the site, students' final progress grades was calculated on a weighted average scale with 60% representing ALEKS weekly topics, 15% depicting district assessment scores, 15% indicating notebook checks, and 10% signifying ALEKS weekly logged time in the program. The department chair stated that math teachers at the site calculated the time and topic scores as a ratio of weekly topics learned to 10 expected attained weekly topics, and weekly hours gained to 10 expected attained weekly hours.

2.1. Preliminary testing

In this investigation, the author sought to predict the relationship between and among continuous variables within a single group. Lodico et al. (2010) asserted that a predictive correlational methodology affords the opportunity to predict the linear relationship between two or more variables after the intervention period. Hence, a multiple regression analysis was applied to investigate the combined and individual strength and the degree of association between the predictor variables on the criterion variables.

Both descriptive and inferential statistics were in the evaluation. Descriptive statistics describes the calculation of simple statistical measures such as mean, standard deviation, and correlational comparisons of all represented predictor variables with criterion variables within the study. Nonetheless, the validity of the study is contingent on the validity of construct measures. Accordingly, a missing value assessment was conducted to identify problematic data and these values were eliminated from the sample set. Additionally, linear models and an ANOVA test were utilized to aid in evaluating the linearity across the domains (Triola, 2012), and the Pearson r correlation coefficient was used to identify the validity of each construct. The latter include an analysis of the magnitude and direction that range from -1 to 1 to describe associations. Cohen's heuristics was instituted to assist in evaluating the correlation coefficient. The Cohen's heuristics correlation provides absolute values of approximately decimal values .1, .3, and .5 to indicate small, medium and large association between variables (Shaw et al., 2016). However, Zacharis (2015) stated that these coefficients are not effective at explaining why there is a relationship or the interactions of these associations (i.e., how two variables vary together). The researcher asserted that a multiple regression analysis affords a better assessment of coefficients while controlling for other variables. As a result of these reviews, this analysis was employed to address the research questions for this evaluation.

The multiple regression analysis was applied to investigate the predictive abilities of the ALEKS constructs (engagement time, retention, and the ratio of topics mastered to topics practiced) on student achievement measures (students' final Algebra 1 course progress grades, and PSAT math scores). The researcher sought to reject the previously stated null-hypotheses and to ascertain an association between the variables that is equal to zero (H₁: p ≠ 0, H₂: p ≠ 0, H_{0 (1)}: p = 0, H_{0 (2)}: p = 0, α ≤ .05: where the predictor or independent variable or = engagement time, retention, and the ratio of topics mastered to topics practiced; and the criterion or dependent variable = students’ final Algebra 1 course progress grades, and PSAT math scores).

2.2. Test to research questions and null-hypotheses

According to Kirkpatrick and Feeney (2016), a multiple regression uses a linear combination of predictors to determine the equation that best predicts the criterion variable and the extent to which this equation predicts the variability in the criterion variable. Hence, a linear model comparison was incorporated to evaluate the collective and individual predictability of the predictor variables on the criterion variables. Kirkpatrick and Feeney (2016) asserted that the hierarchical model provides the opportunity to test if two or more predictor variables collectively predict increased variances in the criterion variable beyond what can be predicted by one alone. The latter provides a better examination of the effect size (R²) between predictor and criterion variable (Kirkpatrick and Feeney, 2016). Consequently, inferential statistics including a multiple regression analysis was employed to evaluate (R²) and to determine the individual and combined proportion of the variance of the predictor variables on the criterion variables.

An ANOVA test of significance (F-test) was used to construct the least-square prediction equation and assess the null-hypotheses that the change in R² is equal to zero in the population. Zacharis (2015) asserted that this test reveals if the final regression model is significant at the .05 level. The F-test determines if the sum of the squares (i.e., regression) divided by the sum of squares (i.e., total) is equivalent to R² (Kirkpatrick and Feeney, 2016). All data were analyzed in the SPSS statistics 23 software with a .05 significance level to determine the association and strength between and among all constructs on students’ achievement.

3. Results

3.1. Data analysis

In this evaluation, a descriptive analysis was conducted on all predictors (engagement time, retention, and the ratio of topics mastered to topics practiced) and criterion variables (students' final Algebra 1 course progress grades and PSAT math scores for the 265 cases. The analysis revealed that, of the predictors, the learners' engagement time had the highest mean score of 155.87 with a standard deviation of 52.67 and ranged from 49.17 to 470.95 total hours. These numbers demonstrate a large spread within the data, which indicated that some students were not spending enough time engaged in the ALEKS program. For example, some students were not logging into the program enough, while others were, perhaps, logging in but not actively working. The participants' ratio of mastered to practiced topics had the second highest mean score of 0.69 with a standard deviation of 0.08 and ranged from 0.44 to 0.87 in ratio scores. The students' retention mean score was 0.59 with a standard deviation of 0.13 and ranged from 0.12 to 0.96 in average proportional scores. Of the criterion variables, the PSAT math variable had a higher mean score of 388.72 with standard deviation of 49.98 and a range span from 240 to 530, and the students’ final progress grade score had a mean of 79.38 with standard deviation 12.82 and a range from 41 to 100. These variables also had a large range and spread within the data. A multiple regression analysis was implemented to determine the linearity of the three predictor variables and their predictive abilities on the criterion variables. No multicollinearity existed, allowing for a clear analysis of the predictive abilities of the independent variables on the dependent variables (see Triola, 2012). Table 1 displays the descriptive statistics of pertinent study variables using measures of central tendency and variability, and Table 2 depicts the intercorrelations with these variables.

Table 1.

Descriptive statistics of pertinent variables.

Variable	M	SD	Min	Max
ET	155.87	52.67	49.17	470.95
mtop	0.69	0.08	0.44	0.87
ren	0.57	0.13	0.12	0.96
PSATm	388.72	49.98	240	530
SFPG	79.38	12.82	41	100

Note. M = mean, SD = standard deviation, Min = minimum, Max = maximum, ET = engagement time, mtop = mastered to practiced topics, ren = retention, PSATm = PSAT mathematics scores, and SFPG = students' final progress grades.

Table 2.

Intercorrelations for pertinent variables.

Variable	1	2	3	4	5
1. ET	--	-.13∗	-.15∗	.43∗∗	-.09
2. ren		--	.35∗∗	-.02	.28∗∗
3. mtop			--	.20∗∗	.18∗∗
4. SFPG				--	.19∗∗
5. PSATm					--

Note. ∗p < .05; ∗∗p < .01.

3.2. Results for research question 1 and the corresponding null hypothesis

The data values for the criterion (dependent) variable of students' final progress grades in the Algebra 1 course were calculated from the weighted averages of students' weekly learned topics ratios, active time in the ALEKS program, notebook checks, and average district assessment scores. The mean score for these averages was 79.38 with a standard deviation of 12.82 and a range from 41 to 100. A bivariate correlation was conducted to determine the relationship between the three predictors and the final progress grade scores. Students' engagement time was the strongest and statistically significant predictor of students' final progress grade scores followed by the mastered to practiced topics. A moderately strong positive relationship existed between engagement time and students' final progress grades (r = .43; p < .001), and the ratio of mastered to practiced topics depicted a slightly medium positive association with final progress grade scores (r = .20; p < .001). No statistically significant correlation existed between students’ retention scores and final progress grades. Table 3 represents the correlational relationship between the three predictors on this criterion variable (SFPG).

Table 3.

Predictor variables and the criterion variable of SFPG score.

Variable	r
ET	0.43∗∗
Mtop	0.20∗∗
ren	-0.02

Note. ∗p < .05; ∗∗p < .01.

After the initial descriptive and correlational analysis, a multiple regression analysis was conducted using final progress grades as the dependent variable. The participants' engagement time, retention, and mastered to practices topics were applied as independent variables. The three predictors explained approximately 25.7% of the variance in students' final progress grade scores. The R² for the full regression model was .26 (F (3, 261) = 30.10; p < .001). The participants' engagement time was the most significant predictor of students' final progress grades (t = 8.56; p < .001). Another significant contributor to the model was the students’ ratio of mastered to practiced topics (t = 5.08; p < .001). In light of these findings, the null hypothesis for research question 1 was rejected and the corresponding alternative hypothesis was retained. Table 4 provides a summary of the full regression analysis for this model.

Table 4.

Summary of full regression for variables predicting SFPG (N = 265).

Variable	B	SE B	β	t
ET	0.46	0.01	0.11	8.55∗∗
ren	-0.07	5.58	-6.67	-1.20
mtop	0.29	8.81	44.71	5.08∗∗

Note. ∗p < .05; ∗∗p < .01; R² = .26; B = unstandardized beta, SE B = standard error; and β = standardized beta.

3.3. Results for research question 2 and the corresponding null hypothesis

The mean score for the criterion (dependent) variable PSATm was 388.72 with a standard deviation of 49.98 and a range from 240 to 530. A bivariate correlation was conducted to determine the association between the three predictors and the PSAT math score. The participants' retention and mastered to practiced topic scores presented a slightly moderate and statistically significant prediction of PSAT math scores, with a slight predictive edge favoring students' retention (r = .28; p < .001) over the ratio of mastered to practiced topics (r = .18; p < .001). The analysis did not reveal a statistically significant relationship between the participants’ engagement time and the PSAT math score. Table 5 describes the correlational relationship between the three predictors on this criterion variable (PSATm).

Table 5.

Predictor variables and the criterion variable of PSATm score.

Variable	r
ren	0.28∗∗
mtop	0.18∗∗
ET	-0.09

Note. ∗p < .05; ∗∗p < .01.

After descriptive and correlational analysis, a multiple regression analysis was conducted using the PSAT math score as the dependent variable. The students' engagement time, retention, and the ratio of mastered to practiced topics were applied as independent variables. The three predictors explained approximately 8.7% of the variance in PSAT math scores. The R² for the full regression model was .09 (F (3, 261) = 8.27; p < .001). The participants’ retention was the only significant predictor of PSAT math scores (t = 3.73; p < .001). In light of these findings, the null hypothesis for research question 2 was rejected and the corresponding alternative hypothesis was retained. Table 6 illustrates the summary of the full regression analysis for this model.

Table 6.

Summary of full regression for variables predicting PSATm (N = 265).

Variables	B	SE B	β	t
ET	-0.05	.06	-0.04	-0.77
ren	0.24	24.13	90.11	3.73∗∗
mtop	0.09	38.08	56.00	1.47

Note. ∗p < .05; ∗∗p < .01; R² = .09; B = unstandardized beta, SE B = standard error; and β = standardized beta.

4. Discussion

The purpose of this study was to determine what factors of the ALEKS ITS are predictive of struggling learners' performance in a blended-learning Algebra 1 course at an inner-city technical high school located in the northeastern United States. Three variables (student retention, engagement time, and the ratio of topics mastered to topic practiced) relating to the theoretical framework behind ALEKS were employed to predict the degree of association on the criterion variable (mathematics competencies) as measured by final course progress grades in Algebra and the PSAT math scores. Findings suggest that the most statistically significant predictor of students’ final progress grades was engagement time followed by the mastered to practiced topics. Nevertheless, these factors were not significant contributors in predicting the PSAT math score, and retention was identified as the lone statistically significant predictor of this criterion variable.

The findings of this study indicate that instructional practices in ALEKS that include increased engagement time and mastery of topics, and that maximize retention in learning, may improve the authentic mathematics learning experiences of struggling students at this location. Based on these findings, one could deduce that increase learning patterns in these constructs in ALEKS are predictive of struggling students' achievement in high school mathematics. The three predictors from this study accounted for approximately 26% of the variance in students' final progress grades which is corroborated with previous research (Bringula et al., 2016; Dani, 2016; Dani and Nasser, 2016). These researchers observed that students' ratio of mastered to practiced topics in ALEKS were significantly predictive of academic success in math courses (Dani, 2016; Dani and Nasser, 2016). They also found that time spent tutoring is significantly correlated with learners' interactions in such modalities (Dani, 2016; Dani and Nasser, 2016). Dani (2016) and Bringula et al. (2016) linked these attributes to learners' prior knowledge and derived attitude. Such information suggests that these students’ prior knowledge and confidence or self-efficacy are essential factors for success in the ALEKS program.

Dani (2016) identified a statistically significant moderately strong and positive correlation between the values of mastered to practiced topics and students' final exam marks. The latter indicates that students with higher yields in this variable are able to master most of the topics they are attempting to learn. This capacity was connected to students' prior knowledge, Dani concluded. Similarly, Bringula et al. (2016) discovered that 11% of the variance in students' time spent in tutoring was due to students' prior knowledge. Dani found that learners' prior knowledge along with their levels of mastered to practiced topics facilitated a higher correlation with final exam scores. These findings indicate that students' percentages of mastered to practiced topics (in ALEKS), along with their time spent in tutoring, are essential predictor of final course grades. This information suggests that instructional practices that maximize students' engagement time in order to increase their values in mastered to practiced topics may support improved progress when learning in the ALEKS platform. For example, instructors may provide timed and topic bound instruction on a daily basis to increase the percentages in students’ mastered topics and may facilitate improved learning in the ALEKS program. Such practices may support the learning of struggling students within this modality, in addition to providing opportunities to build their motivation and confidence when working in the program.

The ALEKS program gathers data pertinent to students mathematical learning patterns and applies this information to personalize learning experiences. Based on the theoretical framework underpinning it, the program can generate personalized sequences of problems that are geared towards the learners' ZPD (Thomas and Gilbert, 2016) and provide guidance via instructional practice and assessment reviews (Craig et al., 2013). Accordingly, the ALEKS ITS may support confidence building for students to problem solve and improve mastery of mathematical concepts. Nonetheless, the lack of continuous step-by-step feedback, instruction relevant to the application of student review capabilities, and a viable process to identify students' retention may limit the program's capacity to maximize the achievement, andragogic processes, and confidence building in struggling learners at the research site (see Dani, 2016; Dani and Nasser, 2016).

According to the department chair at the site, struggling students (at the research location) demonstrated apprehension to making errors or losing topics when working in the ALEKS ITS and when these instances occurred, students became despondent and lost confidence in their math skills and their ability to succeed. A reflection on the letter led this researcher to conclude that such processes may be avoided if ALEKS developers incorporate more scaffolding, additional feedback related to retention as a separate construct, and better alignment review options to support students who are at risk for failure in math courses at this site. These additional supports may improve the ability of students to apply strategies for problem-solving and improve the capability of the program to measure metacognitive skills.

Dani and Nasser (2016) also discussed the topic of building students' confidence in the ALEKS program. These authors expressed the need to provide learners with additional training on how to use the system effectively. The researchers noted that such practices may remove technical barriers and improve students' ability to learn independently while promoting the andragogic skills needed to bolster students’ success in the platform.

The ALEKS instructional program creates more student-centered learning opportunities to apply metacognitive skills to develop motivation and active learning (Cigdem, 2015). According to Butzler (2016) and Duffy and Azevedo (2015), many at-risk students lack the self-regulation learning skills that are essential for success in such platforms. Cigdem (2015) and Greene et al. (2015) identified learners' perceived self-efficacy as one of the factors that influences motivation for learning and performance. Hence, motivation is viewed as an essential variable for the demonstration of self-regulation strategies and learning in online learning settings (Duffy and Azevedo, 2015). This study's findings may assist struggling students in better understanding and applying strategies to address their personal needs to promote self-regulation skills. These students may also be able to build their motivation for learning in this arena.

The findings from this investigation may also further teaching and learning in the ALEKS platform. Program developers and educationalists can apply gained insights to improve the application of this modality with effective instructional practices to better identify students who are at risk for failure and provide learning interventions to address their individual needs. Such actions may bolster the performances of struggling learners within these programs.

4.1. Limitations of the study

Various ITSs are applied in learning institutions across the United States to enhance students' achievements. These ITSs provide specific types of adaptive instruction to remediate and improve the cognitive achievements of learners (Bartelet et al., 2016). Erumit and Nabiyev (2015) noted that ITS programs aim to identify, guide, and improve students' understanding towards acquiring desired behavior. In the current evaluation, a correlational design was applied to assess the predictive impact of three predictor variables (retention, engagement time, and the ratio of mastered to practiced topics) to students’ math achievement (the criterion variable) as measured by PSAT math performance and final progress course grades. As previously stated, the study was centered primarily on 265 students in the 9th and 10th grades at an urban technical high school in the northeastern United States. Students in other cohorts and from other locations did not participate in this research. Nevertheless, the particularities of the sample group for this investigation may have compromised the external validity of the study. Creswell (2012) stated that purposive sampling techniques promote possible selection bias in research studies.

Several threats to internal validity existed in the study as engagement time in the ALEKS ITS was recorded as the total time a student is logged into the program irrespective of their active or inactive performances. The accumulation and combination of these time differential in ALEKS may have impeded the validity of findings germane to student learning. In addition to the latter, the students' ability to work in the program outside of school hours might have compromised the findings as some students might obtain assistance from their parents or older siblings during these time frames. The learners’ ability to participate in such activities may have threatened the accuracy of the ALEKS engagement time construct. Consequently, due to the unique nature of the sample and choice of methodology, as well as the identified predictor variables for this study, results may not be generalized to other ITS programs other than ALEKS or beyond the specific population from which the sample was drawn.

4.2. Recommendations

The results from the investigation coincides with findings by Sullins et al. (2013) which suggest that learners' proficiency in ALEKS can be a potential predictor of their performance on state assessments. These practitioners applied students' mastery of topics in ALEKS as the catalyst for success. Nevertheless, the researchers' use of this construct as the primary driving force of their research contradicts the outcomes of the current study which identify retention as the main variable to influence the state assessment measures. The contradiction in constructs between the two studies may pertain to additional factors that influence student performance at the state level. The findings from this investigation suggest that participants ‘retention accounted for approximately 9% of the variance on the PSAT math score. Based on this result, it was concluded that an estimated 91% of the variance was due to other factors. These additional constructs may include misalignment between students’ level of performance and ITS tools and curriculum, in addition to grade-level standards and instructional strategies to promote engagement and motivation (Hawkins et al., 2017). The latter support calls for additional investigation on this topic at this level of instruction.

A few researchers (Bringula et al., 2016; Dani, 2016), identified learners' prior knowledge and derived attitude to improved achievement in the ALEKS program. These authors used an initial assessment as a predictive construct on students' mathematics success. Dani (2016) asserted that learners' poor language skills is a factor that affects students' ability to learn independently in the ALEKS platform. The current investigation did not apply these constructs as the predictive variables for the analysis. Consequently, additional research that incorporates these elements, as well as other variables that may influence students’ learning and retention in this platform is needed.

The current study centered on the predictive ability of three ALEKS factors (engagement time, retention, and the ratio of mastered to practiced topics) on the math achievement of struggling learners at the high school level. The body of research related to this field of study is limited, and results have been inconsistent (Chappell et al., 2015). As a result, I recommend that future research address other factors of ALEKS and include diverse groups and sizes, as well as the various instructional practices that may impact the application of ALEKS at this instructional level. Such insights may optimize consistency within the body of research that addresses this topic.

4.3. Implications

The findings from this study suggest that participants' engagement time and the ratio of mastered to practiced topics in ALEKS were significant predictors of struggling students' final progress grades in a high school Algebra 1 course, and retention was significantly predictive of PSAT math scores. Based on these results, one could infer that increase learning patterns in these constructs in ALEKS are predictive of struggling students' high school mathematical achievement. Suggesting that improvements in the implementation of the ALEKS program at the research site may optimize the mathematical achievement of struggling learners. Accordingly, mathematics practitioners at this site should apply instructional practices to increase the engagement time and the number of mastered to practiced topics in ALEKS to support improvements in students' final progress course grades, and expand the use of ALEKS retention reviews to optimize learners' retention in mathematics and improve their performance at the state and national level. Educationalist at the site of this investigation may apply such information to increase the quality and effectiveness of combining the ALEKS ITS with best teaching practices to foster improved educational outcomes for struggling learners. The latter may include modifications in the application of the ALEKS program relative to students’ prior knowledge.

Technology developers can incorporate such findings to improve the working efficiency of the ALEKS ITS software program. For example, the developers may incorporate ways to decipher learners' active and inactive time in this platform and provide addition practices to improve students’ retention. The mathematics instructors at this research location can use this information to more effectively identify and address the specific learning needs of their students. These actions may result in struggling learners (at this location) mastering and retaining more math concepts at a quicker pace. Thus, increasing the likelihood of greater success in this milieu, greater math proficiency, reduction in failure rates, higher graduation rates, improve performances on state exams, and a greater range of future job and educational choices.

5. Conclusion

The purpose of this study was to evaluate the predictability of three ALEKS constructs on high school students mathematics success. A multiple regression analysis was utilized to assess the ALEKS data logs of 265 struggling high school students. The predictor variables included students’ engagement time, retention, and the ratio of mastered to practiced topics and the criterion variable comprised of PSAT math score and students final course progress grade. Results indicate that engagement time followed by mastered to practiced topics were the most statistically significant predictors of final progress grade, and retention was identified as the sole statistically significant predictor of PSAT math score. ALEKS developers can apply this information to manifest changes within this technological platform, and educationalists can employ gained insights to maximize instruction and learning in the ALEKS ITS to support the mathematical proficiency of struggling learners. Such actions may bolster the self-efficacy and self-regulation skill of these struggling youth and support their future growth beyond secondary education.

Declarations

Author contribution statement

Nadine Mills: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data associated with this study has been deposited at Mendeley Data under https://data.mendeley.com/datasets/kw8rby2frk/1.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.