Box 3.

Example- calculating stdKt/V

Problem: Let us take the same patient as described in box 2 for calculating stdKt/V. Recalling the problem from box three: a 38-year old female is receiving hemodialysis 6 hours per day, 5 times a week. The dialysis days are Monday, Tuesday, Thursday, Friday, Saturday. Calculate spKt/V from the samples taken on Saturday. Post dialysis blood urea (from sample taken on Friday) is 18 mg/dl. Pre-dialysis blood urea (from sample taken on Saturday) is 52 mg/dl. Weight loss is 1 L. Her weight is 57 Kg and height 165 cm. Additional information: Vascular access is AV Fistula. Weekly ultrafiltration volume is 5400 ml. Residual kidney function (urea clearance, Kru) is 1.4 ml/min.

Solution: We will follow the steps as given below.

Step1: calculate single pool Kt/V: spKt/V has already been calculated for this patient in box 3. It is 1.4993

Step 2: calculate eKt/V.

Using Tattersall equation: eKt/V=spKt/V x T/(T+C)

=1.4993x [(6 x 60)/[(6 x 60) + 35]

=1.4993x [360/(360+35)]

=1.4993x 360/395=1.3665

Step 3: calculate fixed volume model std Kt/V as follows:

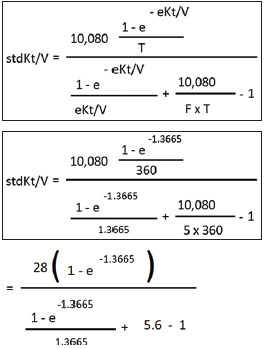As mentioned earlier, ‘e’ is 2.71828 (Euler’s number).

[We will use scientific calculator to calculate the value of e-1.3665 or 2.71828-1.3665]

e-1.3665 or 2.71828-1.3665=0.255

Putting this value in the equation above, we get:

=28 (1-0.255)/[(1-0.255)/1.3665] + 4.6=28 x 0.745/[(0.745/1.3665) + 4.6]

=20.86/(0.5452+4.6)

=20.86/5.1452=4.0543

Step 4: calculate variable volume model stdKt/V by following equation:

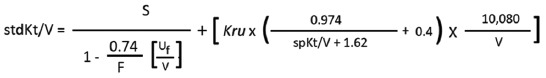S=4.0543; F=5; Uf=5400 ml; Kru=1.4 ml/min; spKt/V=1.4993; V calculated by Watson’s equation=29597.7 ml (already calculated in box 3).

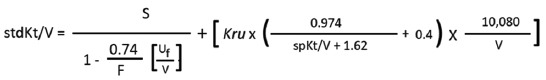=[(4.0543/(1-0.027)] + [ 1.4 x {(0.974/3.1193) +0.4} x 0.34056

=(4.0543/0.973) + [1.4 x (0.3122+0.4) x 0.34056=4.1668 + (1.4 x 0.7122 x 0.34056)

=4.1668+0.3396=4.5064

StdKt/V is 4.5064