Table 1.
Statistical Approaches to Estimation of the Effective Reproductive Number and the Basic Reproductive Numbera
| Approach (Reference No.) | Estimator | Extensions | R Software Package(s) |
|---|---|---|---|
Estimators of 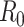
| |||
| White and Pagano (34)—serial interval known |
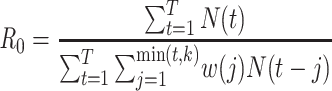
|
Imported cases (8, 47) Bayesian implementation (35, 36) Heterogeneity (58) |
R0 package (47) function: est.R0.ML, option unknown.GT = F |
| White and Pagano (34)—serial interval unknown | Maximize the likelihood w.r.t. 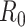 and and 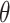 : :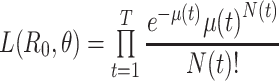 , ,where 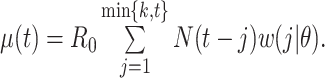
|
Imported cases (8, 47) Bayesian implementation (35, 36) Heterogeneity (58) |
R0 package (47) function: est.R0.ML, option unknown.GT = F |
| Bettencourt et al. (33) |
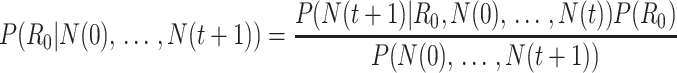
|
Imported cases (8, 60) | R0 package (47) function: est.R0.SB |
Estimators of 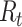
| |||
| Instantaneous reproductive number (32, 39) |
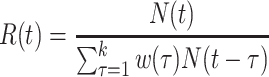
|
Importation (51) Smoothing (39) |
EpiEstim package (39, 52) |
| Case reproductive number (1) |
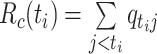 ,
,where 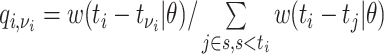
|
Heterogeneity (56, 57) Importation (47) |
R0 package (47) est.R0.TD function EpiEstim package (39, 52) |
a Notation: 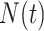 , number of new cases at time
, number of new cases at time 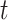 ;
; 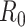 , basic reproductive number;
, basic reproductive number; 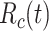 , case reproductive number at time
, case reproductive number at time 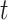 ;
; 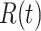 , instantaneous reproductive number;
, instantaneous reproductive number; 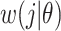 , probability of a serial interval of length j, where
, probability of a serial interval of length j, where 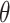 are the parameters of the serial interval density function.
are the parameters of the serial interval density function.
