FIGURE 1.

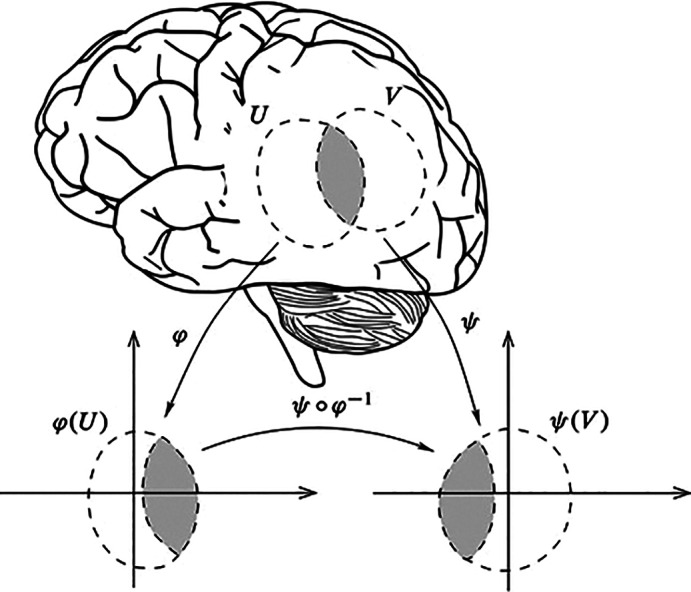
An n‐dimensional manifold M can be described locally by the n‐dimensional real space ℝ ⁿ. A local chart (φ, U) is an open subset of the manifold U ⊆ M together with a one to one map φ: U→ℝ ⁿ from this subset to an open set of the Euclidean space. The piecewise one‐to‐one mapping to the Euclidean space allows generalizing Euclidean space properties onto manifolds. A transition map between two open subsets of ℝ ⁿ provides a way to compare two charts of an atlas