Abstract
The coronavirus disease 2019 (COVID-19) is rapidly becoming one of the leading causes for mortality worldwide. Various models have been built in previous works to study the spread characteristics and trends of the COVID-19 pandemic. Nevertheless, due to the limited information and data source, the understanding of the spread and impact of the COVID-19 pandemic is still restricted. Therefore, within this paper not only daily historical time-series data of COVID-19 have been taken into account during the modeling, but also regional attributes, e.g., geographic and local factors, which may have played an important role on the confirmed COVID-19 cases in certain regions. In this regard, this study then conducts a comprehensive cross-sectional analysis and data-driven forecasting on this pandemic. The critical features, which has the significant influence on the infection rate of COVID-19, is determined by employing XGB (eXtreme Gradient Boosting) algorithm and SHAP (SHapley Additive exPlanation) and the comparison is carried out by utilizing the RF (Random Forest) and LGB (Light Gradient Boosting) models. To forecast the number of confirmed COVID-19 cases more accurately, a Dual-Stage Attention-Based Recurrent Neural Network (DA-RNN) is applied in this paper. This model has better performance than SVR (Support Vector Regression) and the encoder-decoder network on the experimental dataset. And the model performance is evaluated in the light of three statistic metrics, i.e. MAE, RMSE and R2. Furthermore, this study is expected to serve as meaningful references for the control and prevention of the COVID-19 pandemic.
Keywords: Coronavirus disease 2019 (COVID-19), eXtreme gradient boosting (XGB), SHapley additive exPlanation (SHAP), Dual-stage attention-based recurrent neural network (DA-RNN)
Introduction
In December 2019, the coronavirus disease 2019 (COVID-19) was identified in Wuhan, the capital of the Hubei province of China. Since then, the increasing number of COVID-19 infected cases has been reported in many countries. As of September 30, 2020, the COVID-19 pandemic has resulted in more than 34 million confirmed cases worldwide. Since the COVID-19 pandemic has intensively threated public security and peoples’ health, it was immediately attracted the attention of scholars from many different research fields. They attempted to model and analyze the spreading path of this pandemic, so as to find the appropriate strategies or suggestions to reduce the spreading risk of COVID-19. The COVID-19 virus is mainly transmitted through polluted air or water originated from respiratory droplets [1–5], fecal contamination [6], etc. of infected persons. Known the fact that COVID-19 virus can survive in the air for several hours, resulting in potential aerosolized transmission for the certain polluted region [7]. Hence, due to a period of close contact among peoples, cluster infections, e.g. family cluster, community transmission, etc., played important roles in the rapid evolution of COVID-19 transmission [8].
Additionally, understanding the relationship between the confirmed COVID-19 cases and their influential factors is vital for the pandemic risk management and containment. Current studies have shown that multiple critical factors (e.g. environmental conditions, air pollution, population density, etc.) may contribute to the severity and prevalence of the COVID-19 [9–11]. For instance, through data analysis, Wu et al. [12] revealed that temperature and relative humidity are both negatively correlated with the daily new cases and deaths of this pandemic. Besides, it is found that air pollution was associated with COVID-19 infection [13, 14], which could partially explain the impact of the international lockdown. Notice that, population mobility also had a great impact on the COVID-19 pandemic [15].
Taken the aforementioned propagate characteristics (i.e. spreading path and influential factors) of the COVID-19 into account, some researchers are committed in analyzing and forecasting the confirmed cases of this pandemic [16–18]. For instance, Hernandez-Matamoros et al. [19] forecasted the COVID-19 cases in six geographical regions by means of ARIMA (Auto-Regressive Integrated Moving Average) model and polynomial functions. Their findings show that there was a strong relation between COVID-19 behavior and population in the same region. Based on the population flow data, Jia et al. [20] not only proposed a spatio-temporal model to forecast the distribution of confirmed COVID-19 cases in China, but also identified regions that had a high risk of transmission. Besides, Ghosh et al. [21] analyzed the inter-state variations in the potential for transmission of COVID-19, and assessed the exposure, preparedness and resilience capacity in different states of India. Moreover, Ndairou et al. [22] proposed a compartmental mathematical model to analyze the spreading process, particularly focused on the transmissibility of super-spreaders individuals.
Previous studies often applied the SIR (Susceptible Infected Recovered) model for analyzing the potential impact of the pandemic [23–25]. These SIR-type models are helpful for policy-decision makers to carry out rapid actions to minimize the risks and losses caused by the pandemic. In a recent study, confirmed COVID-19 cases of a few European countries, e.g., Denmark, Belgium, Germany, etc., were modeled and estimated by ARIMA, NARNN (Nonlinear Autoregression Neural Network) and LSTM (Long-Short Term Memory) approaches, respectively [26]. Besides, artificial intelligence techniques are used to learn interesting information and patterns from COVID-19 genome sequences [27]. As the COVID-19 disease spreads worldwide and the regional resilience requirement rises, daily-level regional data are needed for a detailed analysis and forecasting, e.g., population mobility, smoking rate, and the number of hospitals. By collecting daily state-level data from each state of US, this study can produce targeted forecasts of the confirmed COVID-19 cases and further provide valuable insights for policymakers to take proper measures correspondingly.
In the United State, the first case of the COVID-19 pandemic was confirmed in Washington state. Shortly afterwards, multiple states have also experienced a significant increase in the number of infection cases and deaths. On March 17, 2020, all states across the United States had confirmed cases of COVID-19 [28], and as of September 30, 2020, more than 200,108 deaths and over 7,183,104 cases have been confirmed [29]. As known that most states in the US are differed in natural environment, geography and economy, hence it requires a novel perspective to capture the spread of COVID-19. Due to the rapid spreading and high mortality properties of the coronavirus disease, a series of social distancing interventions have been implemented around the country, including closures of cinemas, restaurants, and schools [30], and a great number of corporations and businesses have encouraged their staff to work remotely. Notice that, these interventions have significantly reduced the infection rate of the COVID-19 pandemic and reflected on the daily confirmed cases. To better forecast the confirmed cases of COVID-19 in the United States, this study performs a cross-sectional analysis and one-step-forward forecasting on the pandemic. The entire research process can be divided into three stages. In the first stage, the daily time-series data and the regional attributes of COVID-19 in all states across the US are collected. The regional attributes offer the static information within the certain region. In the second stage, a cross-sectional analysis is conducted based on the static attributes from different states. This study applies XGB (eXtreme Gradient Boosting) algorithm [31] and SHAP (SHapley Additive exPlanation) [32] for determining the top important features that significantly influence the infection rate of COVID-19 (the total number of the confirmed cases per 1000 people). In addition, a comparative study is carried out by using RF (Random Forest) and LGB (Light Gradient Boosting) models. In the third stage, both temporal and static features obtained from the second stage are considered. This study uses them as inputs of the Dual-stage Attention-based Recurrent Neural Network (DA-RNN) [33], which is one of the state-of-the-art algorithms in time series forecasting that considers both varying influences and long-short term memory from different features. Experiment results demonstrate that utilizing detailed static attributes and daily time-series data from each state of the US can greatly improve the forecasting accuracy of the pandemic models. Furthermore, the forecasting performance of the DA-RNN is superior to the Support Vector Regression (SVR) and the encoder-decoder network using three representative states, i.e. Washington, Ohio, and Los Angeles.
The contribution and innovation of this study can be explicated as follows. Firstly, XGB algorithm, which is based on the gradient boosting decision tree, is adopted and can process static attributes and determine the important features that influence the infection rate of COVID-19 in each state of the US. Meanwhile, SHAP is applied to increase the interpretability of XGB. Second, the DA-RNN model is applied to forecast the confirmed cases of COVID-19 in the US. Given that pandemic forecasting is strongly related to the surrounding environment and historical confirmed case data, DA-RNN is suitable for pandemic forecasting problems. Through the comparative data experiment within Washington, Ohio, and Los Angeles, DA-RNN proves its superiority in improving forecasting accuracy over the SVR and the encoder-decoder network. In these cases, the model performance is evaluated by MAE, RMSE and R2.
The rest of this paper is organized as follows. Section 2 demonstrates the proposed framework. In Section 3, a cross-sectional analysis is conducted based on the spatial data of each state in the United States. Section 4 proposes a DA-RNN model to forecast the confirmed cases of COVID-19. Subsequently, the comparative experimental results are presented with a detailed analysis. At last, Section 5 summarizes the entire work of this paper and outlines the directions of the future work.
Proposed framework
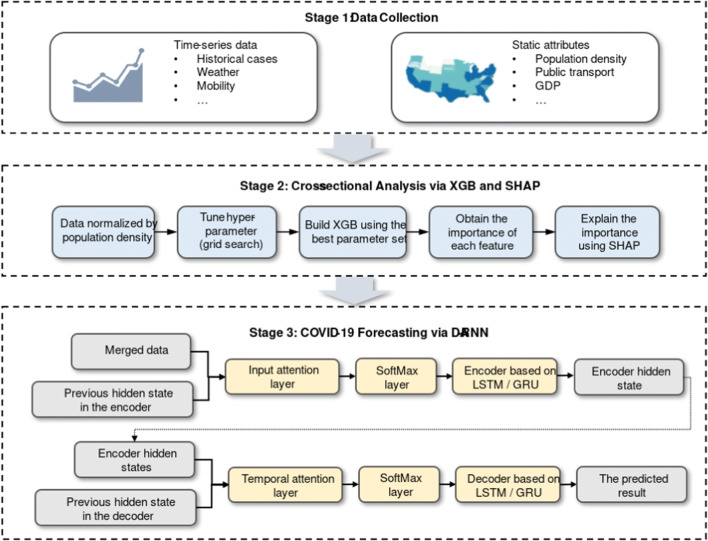
Historical time series of infected cases and static attributes within a particular region, e.g. population index, economic indicators, etc. [34–37], is crucial for regionally forecasting the number of COVID-19 confirmed cases. In this regard, following proposed framework is constructed for combining temporal and static variables and it can be divided into three stages, as shown in Fig. 1.
Fig. 1.
The proposed framework
In the first stage, both the daily time-series data of infected cases and regional attributes of each state are collected. In the second stage, cross-sectional analysis is conducted based on the aforementioned static attributes. In general, XGB is relatively robust if there are uninformative and redundant features, and it can be applied to evaluate features importance since it consists of tree-based structure. For the aim of comparison, we also presented RF (Random Forest) and LGB (Light Gradient Boosting) as the important feature selectors. Nevertheless, the fact is that interpretability and high accuracy of a specific model are often incompatible, especially for ensemble algorithms, e.g. RF, XGB, LGB. To overcome this drawback, SHAP is applied to exhibit the results of feature importance. For this study, SHAP cannot only obtain the feature importance through the marginal contribution of each feature, but further analyze the individualized explanation for each state, thereby helping to select the dominant features for the subsequent prediction. In the third stage, a DA-RNN is proposed for pandemic forecasting based on the temporal and static variables. DA-RNN considers both spatial and temporal effect to forecast the number of COVID-19 confirmed cases. Specifically, the input attention layer of DA-RNN can adaptively extract relevant input features from merged data at each step by referring to the previous encoder hidden state. The temporal attention layer is then utilized to select relevant encoder hidden states across all the steps. Applying this two-stage attention scheme, the proposed model can make more accurate forecasting.
Cross-sectional analysis
Dataset
Data on this research is collected from publicly accessible secondary sources. The overall dataset can be generally separated into two parts, i.e. spatial data and time-series data. Spatial data contains demographic, public health, and other relevant COVID-19 predictors for 50 states and District of Columbia in the United States. A variety of 17 socioeconomic, behavioral, environmental, and demographic factors were compiled and considered as static features, with the infection rate as the target variable. Table 1 provides the names and definitions of these variables, where the infected rate is given as :
| 1 |
Table 1.
Static features used in this study with their definitions
| Theme | Feature Name | Description |
|---|---|---|
| Socioeconomic | Income | Income per capita ($) |
| GDP | GDP per capita | |
| Unemployment | Unemployment as a percentage of the state labor force | |
| Health spending | Spending for all health services ($) | |
| Behavioral | Smoking rate | Percentage of smokers |
| Environmental | Temperature | Average temperature in 2019 |
| Pollution | Measurement of the public’s exposure to particulate matter | |
| Demographic | Urban | Percentage of the population living in an urban environment |
| Pop density | Density of people per meter squared | |
| Sex ratio | Males / Females | |
| Flu deaths | Influenza and Pneumonia death rate per 100,000 people | |
| Respiratory deaths | Chronic lower respiratory disease rate per 100,000 people | |
| Physicians | Number of physicians and surgeons per 1000 people | |
| Hospital beds | Number of hospital beds per 1000 people | |
| Age 65+ | Percent of 65 years and over | |
| Major airports | Number of medium and large airports | |
| Public Transportation | The proportion of people who use public transportation when they go to work | |
| Target variable | Infected rate | Total number of confirmed COVID-19 cases per 1000 people as of September 30, 2020 |
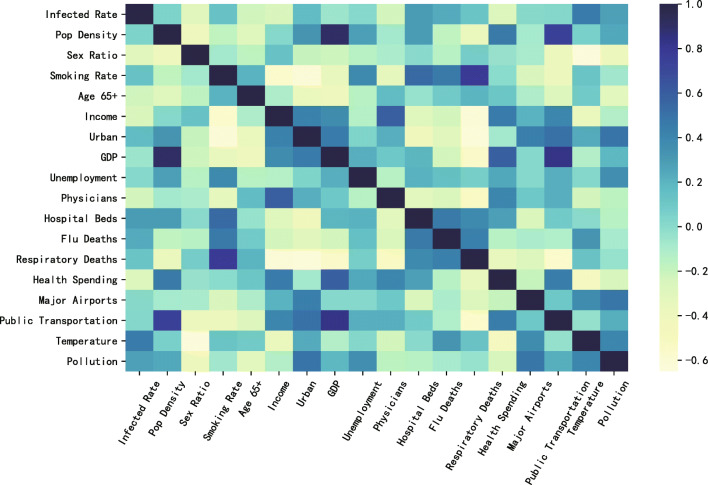
Based on the features within Table 1, we calculated the covariance matrix, which is shown as a heatmap (see Fig. 2). In this heatmap, the low linear correlation between the features and the target variable, i.e. infection rate, can be found. Besides, some features have high linear correlation with others. For instance, “Smoking Rate” is highly correlated with “Respiratory Deaths”, while “Population Density” is highly correlated with “GDP”. Therefore, this study adopted XGB and other tree-based integration algorithms, which can automatically handle the collinearity characteristics. SHAP is applied to further analyze these features and find their effect on the infection rate of COVID-19. Thereafter, we choose the main factors for being substituted into the prediction models.
Fig. 2.
The heatmap of covariance matrix of static features
XGB and SHAP
XGB (eXtreme Gradient Boosting) is an optimized ensemble algorithm based on the gradient boosting decision tree, which can build CARTs (Classification and Regression Trees) efficiently and operate in parallel. Assume that a dataset with n states’ data in the US is Dn × m = {(xi, yi), xi ∈ Rm, yi ∈ R, i = 1, 2, …, n} in which xi is i-th state of m dimension vector, in which m represents the number of static attributes. In this study, yi is the true value of the infection rate, i.e. the total number of the confirmed cases per 1000 people, of i-th state. The estimation of infection rate in the light of XGB was obtained by summarizing K additive CARTs as Eq. (2).
| 2 |
where K is the number of trees; F denotes the set of all possible CARTs.
Rather than using first-order information by means of gradient boosting decision tree (GBDT) when calculating negative gradients, XGB applies the second order Taylor’s series expansion to obtain the first- and the second-order information, and utilizes the complexity of the model as a regularization term in the objective function to avoid overfitting [38]. The specific objective function for XGB to be optimized at each iteration can be expressed as follows:
| 3 |
where obj(t)is the objective function at round t, is the infection rate prediction of the i-th instance at (t − 1)-th iteration, Ω(ft) represents the regular term, which considers the complexity of this model, ft(xi) is the t-th iteration tree output, gi and hi are the first and the second order gradient, calculated as follows.
| 4 |
| 5 |
where l is a differentiable convex loss function that measures the difference between yi and .
After a series of derivation, the objective function can be expressed by Eq. (6):
| 6 |
where T represents the number of leaf nodes; λ and γ are the penalty coefficients. Eq. (6) is also called the scoring function and can be applied to select the best segmentation point while constructing CARTs. XGB can evaluate the feature importance according to scoring function. For a single tree, the feature importance is determined by comparing the performance measure before and after each feature segmentation. Performance measures of the feature importance consist of “gain”, “frequency” and “coverage”, where the first term is the main reference factor, the middle term counts the times of appearance of a feature in all constructed trees, and the last term is the relative number of observations related to this feature, respectively. Subsequently, the results of a feature in all trees are averaged to obtain the importance value.
While feature importance can be incidentally obtained through the XGB model, the gain, frequency, and coverage methods above are all heuristic and global feature attribution methods. This means that the individualized explanation for each prediction is not available. In addition, the feature importance calculated from these methods is inconsistent, which prevents meaningful comparison of attribution values among features. To overcome this circumstance, SHAP (SHapley Additive exPlanation) is applied to make prediction models explainable and analyze individual prediction samples. SHAP is an additive interpretation model based on an explanation model g, defined as a linear function of binary variables:
| 7 |
where g is an explanation model; reveals feature xp exists or not, respectively; ϕp is the Shapley value of feature xp; ϕ0 is a constant.
In the tree model, to calculate the SHAP value for feature xp, we need to calculate the Shapley values of all possible feature permutations (different sequences are included) and do the weighted addition while feature xp is fixed. The Shapley value is calculated as:
| 8 |
where S is the subset of entire features, val(S) is the output value when input is the specific permutation S. For the weight, there are m! permutations for m features, and when feature xp is fixed, there are (m−| S | −1) ! ∣ S ∣ ! permutations.
As an additive feature attribution method, three characteristics of SHAP are defined as “local accuracy”, “missingness” and “consistency”, where the first term means that the sum of the feature attributions is equal to the output of the function in question, the middle term means that missing features are attributed no importance, and the last term states that changing a model, such that observing a feature has a larger impact on the model, will never decrease the attribution assigned to that feature [39].
Hyperparameter setting and evaluation metrics
In this section, XGB based on the regression tree is applied to fit the relationship between the target variable (i.e. infection rate) and the independent features, e.g. population index, economic indicators, etc. Since infection rate, defined as confirmed cases of COVID-19 per 1000 people, belongs to numeric values, feature evaluation is essentially a sensitivity analysis on a regression solution. Given that the target variables are normalized by population, some other features in the independent variables, e.g. the number of registered physicians and hospital beds, are also measured by the population of the region. We applied the XGB algorithm on state-by-state dataset and compared its performance with RF and LGB. Since these models are all tree-based models, it is not necessary to normalize samples, and features from different dimensions will not significantly affect the results. To ensure the validity of these models, dataset is divided into the train set and test set with the ratio of 7:3. To prevent overfitting problems and control the model complexity, a proper six-fold cross validation method is chosen to train multiple sets of different hyperparameters. Since overfitting often occurs when a model starts to learn noises and random fluctuations, and eventually treats them as the meaningful facts [40].
Table 2 presents the hyperparameter values of XGB, RF, and LGB utilized in this study. For XGB, the number of iterations equals the number of trees for the approach. The subsample is the percentage of samples used per tree. The maximum depth of the tree represents the maximum number of nodes that are traversed. The learning rate, also known as the concept of shrinkage, is applied to control the weighting of new trees added to the model leading to a more robust model. The parameter “colsample bytree” prevents overfitting by subsampling the features. “Lambda” and “alpha” are L2 and L1 regularization terms of weights, and their increments make the model more conservative.
Table 2.
The hyperparameter values of XGB, RF, and LGB utilized in this study
| Parameters of XGB | Values | Parameters of RF | Values | Parameters of LGB | Values |
|---|---|---|---|---|---|
| number of iterations | 150 | number of iterations | 150 | number of iterations | 150 |
| max depth | 3 | max features | default | max depth | 3 |
| subsample | 0.7 | max depth | 3 | subsample | 0.7 |
| colsample bytree | 0.7 | min_samples_split | 2 | colsample bytree | 0.7 |
| lambda | 2 | min_samples_leaf | 1 | min_child_weight | 1 |
| alpha | 1 | min_weight_fraction_leaf | 0 | num_leaves | 40 |
| learning rate | 0.05 | max_leaf_nodes | None | learning_rate | 0.05 |
Due to the difficulty in evaluating the model performance by means of a solo metric, MSE (Mean Square Error), RMSE (Root Mean Square Error), and MAE (Mean Absolute Error) are selected as evaluation indexes. The calculation formulas of these statistic metrics are listed as follows:
| 9 |
| 10 |
| 11 |
where N is the number of samples, yi is the i-th actual value of infection rate; is the i-th predicted value of infection rate.
Results and discussion
Table 3 shows the performance results of XGB, RF, and LGB. According to the data experimental results of evaluation indexes, i.e. MSE, RMSE, MAE, the XGB model has better performance than other models.
Table 3.
The performance results of XGB, RF and LGB
| RMSE | MAE | MSE | |
|---|---|---|---|
| XGB | 5.0172 | 6.3516 | 25.1722 |
| RF | 6.3216 | 7.5264 | 39.9626 |
| LGB | 6.8234 | 6.6538 | 77.8523 |
We analyze and compare the data experimental results obtained by XGB, LGB and RF models using the SHAP tool. For the sake of brevity, this section merely focuses on interpreting the output of the best model, i.e. XGB. To explore the influence factors at different stages of the pandemic, this section employs two sets of data to calculate the feature importance using XGB model, namely information gain of XGB and mean magnitude of SHAP values. Tables 4 and 5 shows the feature importance calculated based on the two datasets during different time period: the first dataset is from March 1 to June 30, and the second is from March 1 to September 30, respectively.
Table 4.
The feature importance calculated by using data from March 1 to June 30
| No. | Features | Gain of XGB | Mean magnitude of SHAP values |
|---|---|---|---|
| 1 | Pop Density | 110.4355 | 1.4059 |
| 2 | Public Transportation | 39.9490 | 0.9363 |
| 3 | Pollution | 20.2100 | 0.6166 |
| 4 | Sex Ratio | 3.8168 | 0.5133 |
| 5 | Urban | 4.4805 | 0.4145 |
| 6 | Income | 26.9567 | 0.3677 |
| 7 | Hospital Beds | 2.4753 | 0.3319 |
| 8 | Respiratory Deaths | 2.3760 | 0.3230 |
| 9 | Physicians | 3.1678 | 0.3216 |
| 10 | Flu Deaths | 1.8414 | 0.2705 |
| 11 | Age 65+ | 13.0877 | 0.2506 |
| 12 | Major Airports | 11.6312 | 0.1672 |
| 13 | Unemployment | 5.6695 | 0.1666 |
| 14 | GDP | 6.8395 | 0.1338 |
| 15 | Health Spending | 2.6873 | 0.1099 |
| 16 | Temperature | 0.6306 | 0.0667 |
| 17 | Smoking Rate | 0.4426 | 0.0527 |
Table 5.
The feature importance calculated by using data from March 1 to September 30
| No. | Features | Gain of XGB | Mean magnitude of SHAP values |
|---|---|---|---|
| 1 | Temperature | 146.9716 | 1.3928 |
| 2 | Age 65+ | 82.3948 | 1.0826 |
| 3 | Pollution | 117.6348 | 0.7934 |
| 4 | Sex Ratio | 71.3326 | 0.7878 |
| 5 | Hospital Beds | 86.3513 | 0.5321 |
| 6 | Physicians | 59.3828 | 0.3353 |
| 7 | Flu Deaths | 70.7815 | 0.3350 |
| 8 | Pop Density | 24.6166 | 0.3278 |
| 9 | Smoking Rate | 38.8826 | 0.2811 |
| 10 | Income | 54.6326 | 0.2498 |
| 11 | Urban | 57.2029 | 0.1965 |
| 12 | Health Spending | 30.7574 | 0.1560 |
| 13 | Major Airports | 21.3473 | 0.1254 |
| 14 | Unemployment | 34.6735 | 0.1231 |
| 15 | GDP | 42.9217 | 0.0892 |
| 16 | Respiratory Deaths | 51.7551 | 0.0883 |
| 17 | Public Transportation | 76.4803 | 0.0460 |
As shown in Tables 4 and 5, the ranking of feature importance calculated in XGB by gain is slightly different from the average absolute value of SHAP. The motivation of gain is mostly heuristic, indicating that gain is not a reliable measure of global feature importance. In contrast, a more robust estimation of the feature importance based on the mean magnitude of SHAP values is performed. At the early stage of the pandemic, the proportion of people taking public transportation to work place as well as the population density were the most important factors affecting the infection rate in a certain region. With the spread of the pandemic, the intervention of certain social distance policies could be a major reason for causing changes in influence factors. As a result, temperature and the percentage of people over 65 become the most important factors that affect the infection rate.
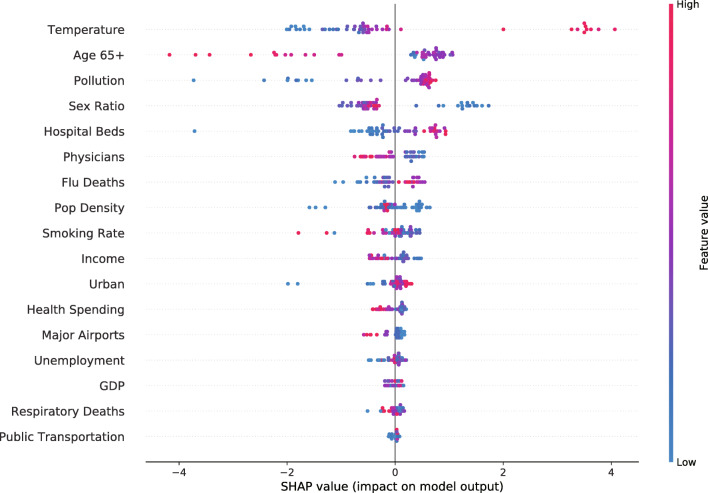
More practically, the following presentation is based on the recent dataset, i.e., from March 1 to September 30. Except from global feature importance, we also analyze the Shapley value for each of aforementioned static feature. In Fig. 3, the horizontal axis represents the Shapley value, where a positive and negative value stand for a higher and lower default probability, respectively. The vertical axis represents features sorted by global importance. The color of these dots indicates the magnitude of important values, notice that from red to blue, the color reveals from higher to lower important values, respectively. If one feature changes from blue to red on the horizontal axis, the Shapley value increases, thereby this feature has a monotonically increasing relationship with the target variable, i.e. infection rate. In this case, it can be found that “Temperature”, “Pollution”, “Hospital Beds”, “Flu Deaths” and “Urban” are positively related to the targeted variable.
Fig. 3.
A summary plot of the impact of each static feature on the model output
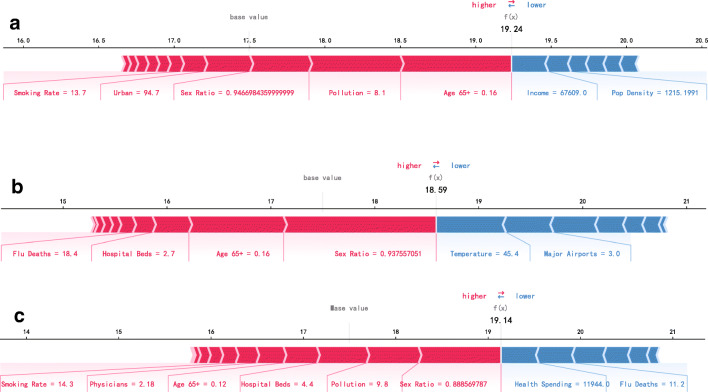
Using SHAP, the feature contributions to each state can be evaluated and visualized. In this part, we display the three states for analysis: New Jersey, New York and District of Columbia, as shown in Fig. 4. The feature magnitudes are shown below the horizontal axis, sorted by absolute value. The width of the arrow represents the SHAP value of each feature. The arrow in pink indicates that the SHAP value of this feature is positive while the blue is negative. For New Jersey, the prediction of XGB is 19.24 [see Fig. 4], which is different from the base value (the average output over the training dataset). “Age 65+” and “Pollution” are powerful forces to drive the prediction accuracy up. For New York, main reasons behind the increase in the prediction up are “Sex Ratio” and “Age 65+”. For District of Columbia, the SHAP value of “Health Spending” is negative, which slowed down the prediction up to a certain extent.
Fig. 4.
Three examples illustrating the relative contributions of static features to the predicted confirmed cases of COVID-19 per 1000 people. (a) New Jersey (b) New York (c) District of Columbia
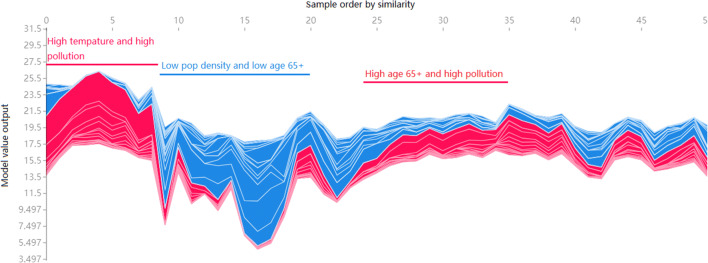
Rotate all state explanations of feature importance by 90 degrees anticlockwise, and stacked horizontally, the explanations for the entire dataset can be seen, as shown in Fig. 5. Each vector is sorted by similarity. There may be similar reasons for the predicted results in different states. With high temperature and pollution, XGB model tends to predict a high infection rate. In contrast, low population density and small amount of people over the age of 65 lead to low infection rates.
Fig. 5.
State samples sorted by the explanation similarity
Forecasting
Dataset
To forecast the confirmed cases of COVID-19, this study has collected daily time-series data of COVID-19 in each state of the United States from March 1, 2020, to September 30, 2020. This dataset consists of 10 types of time-series data related to COVID-19 for each region in the United States. Since several temporal variables (e.g. mobility_retail_and_recreation, mobility_grocery_and_pharmacy, mobility_parks, mobility_transit_stations, mobility_workplaces, and mobility_residential) are multicollinearity, the average mobility is used instead. Table 6 illustrates the necessary information of these temporal data, including variable names, variable types, and their descriptions.
Table 6.
Temporal variables utilized in this study with their definitions
| Variable Name | Type | Description |
|---|---|---|
| Total confirmed cases | Integer | Cumulative sum of cases confirmed after positive test to date |
| New confirmed cases | Integer | Daily cases confirmed after positive test |
| mobility_retail_and_recreation | Double | Percentage change in visits to retail and recreation locations compared to baseline |
| mobility_grocery_and_pharmacy | Double | Percentage change in visits to grocery and pharmacy locations compared to baseline |
| mobility_parks | Double | Percentage change in visits to park locations compared to baseline |
| mobility_transit_stations | Double | Percentage change in visits to transit station locations compared to baseline |
| mobility_workplaces | Double | Percentage change in visits to workplace locations compared to baseline |
| mobility_residential | Double | Percentage change in visits to residential locations compared to baseline |
| Average mobility | Double | The average value of mobility_retail_and_recreation, mobility_grocery_and_pharmacy, mobility_parks, mobility_transit_stations, mobility_workplaces and mobility_residential |
| Average temperature | Double | Recorded hourly average temperature |
DA-RNN
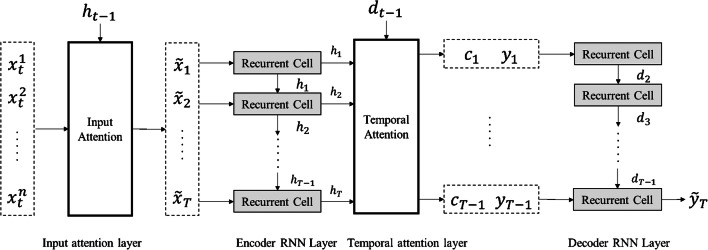
Although various pandemic prediction models have been developed, few of them can properly capture the long-term temporal dependencies and select the relevant time series for prediction. This study proposes a Dual-stage Attention-based Recurrent Neural Network (DA-RNN) to solve these two problems. Within DA-RNN model, it involves two attention layers: the first is an input attention layer that determines which feature should be given more attention than the others; the second is a temporal attention layer that determines the weight of importance for each historical temporal step [41, 42]. Subsequently, we concatenated the output from the second attention layer to the historical information, so as to forecast the confirmed cases of COVID-19 in the next time step, as shown in Fig. 6.
Fig. 6.
Graphical illustration of the dual-stage attention-based recurrent neural network
Given the previous values of the target series is yt = {y1,…yT − 1}, and the sequence of the exogenous time series is xt = {x1,…xT}. The input attention layer calculates the attention weights αt for multiple exogenous time series xt conditioned on the previous hidden state ht − 1 in the encoder, and then feeds the computed into the encoder RNN layer. The calculation formula of is as follows.
| 12 |
The temporal attention system then calculates the attention weights based on the previous decoder hidden state dt − 1 and represents the input information as a weighted sum of the encoder hidden states across all the time steps. The generated context vector ct is then used as an input to the decoder RNN layer. The output of the last decoder recurrent cell is the predicted result.
Both the encoder and the decoder layer are composed of recurrent cells. These cells maintain and update their hidden state to store previous information. This study uses Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) as recurrent cell respectively, and compares the performance of these two models.
In LSTM-based model, each LSTM cell consists of an input gate, an output gate and a forget gate. For instance, the encoder LSTM cell receives the calculated at time t, the hidden state ht − 1 and the cell state st − 1 at time t − 1. The calculation formulas of input gate, forgotten gate and output gate are as follows:
| 13 |
| 14 |
| 15 |
Where it represents the input gate, which is used to add information to the cell state. ft represents the forget gate, which is responsible for discarding cell state information. ot represents the output gate that controls how much ct outputs to the next hidden state ht. wi wf, wo, wc are the weight matrices. bf, bo, bc are the bias vector and σ is the activation function.
The cell state st is updated through input and historical information. The calculation formula is as follows:
| 16 |
| 17 |
The hidden state after the update is calculated as follows:
| 18 |
In GRU-based model, each GRU cell consists of an update gate and a reset gate, similar to the forget gate and input gate within the LSTM cell. The update gate defines how much previous memory to keep around and the reset gate defines how to combine the new input with the previous memory. Unlike LSTM, GRU completely exposes its memory content and does not have separate memory cells. Therefore, GRU is much simpler to compute and implement.
The DA-RNN constructed in this study combined two types of inputs, i.e. static features and temporal features. For a given dataset with nd temporal features of length ld, we produce ns additional time series of length ld using static feature. The temporal features consist of new confirmed cases, total confirmed cases, average temperature and average mobility. By rolling time series of the previous period forward, we can forecast the total confirmed cases on the next day in a step-wise manner.
Hyperparameter setting and evaluation metrics
The overall dataset is divided into the train set and test set with the ratio of 7:3. To improve the convergence speed and performance effectively, a max-min normalization process before feeding to the network is needed, and it is expressed as follows:
| 19 |
in which x is a specific feature; xmax, xmin are the maximum and minimum value of this feature, respectively.
In this study, both DA-RNN and the encoder-decoder network employ Adam as an optimizer. Mean squared error is utilized as a loss function. During the training process, we set the learning rate as 0.001 reduced by 0.1 after each 10,000 iterations, the size of hidden states for both encoder and decoder as 128, epochs as 300, batch size as 256 and window size as 10.
Three evaluation metrics are used to evaluate the performance of the proposed model, i.e., RMSE, MAE and Correlation coefficient (R2). The calculation formula of R2 is shown below.
| 20 |
Where N is the number of samples, yi is the i-th actual value, is the i-th predicted value, is the average value.
Results and discussion
In this section, we select several states that are most representative of the overall situation of the pandemic in the United States, and then make targeted predictions in these states. To determine the representative states, we use the Pearson correlation coefficient to examine the relationship between the confirmed cases in the United States and that in each state. The top three states with the highest correlation coefficients are Washington, Ohio, and Los Angeles, i.e. 0.9993, 0.9989 and 0.9969, correspondingly.
Subsequently, we carry out a series of experiments by means of GRU-based and LSTM-based DA-RNNs. RMSE, MAE and R2 are applied to measure and evaluate the performance of two models. Meanwhile, Support Vector Regression (SVR) and the encoder-decoder network are selected as comparison models. Different from DA-RNN, the encoder-decoder network based on LSTM does not utilize the attention mechanism. Tables 7, 8, and 9 respectively show the prediction results on three different states (i.e. Washington, Ohio and Los Angeles). It is worth noting that MAE and RMSE are not comparable due to different data ranges from state to state.
Table 7.
The prediction results using the data in Washington
| Model | Training | Testing | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | R2 | MAE | RMSE | R2 | |
|
LSTM-based DA-RNN |
305.2435 | 397.7334 | 0.9824 | 496.2958 | 669.4930 | 0.9342 |
|
GRU-based DA-RNN |
253.4356 | 372.8175 | 0.9997 | 463.6574 | 654.5355 | 0.9474 |
| Encoder-Decoder | 595.3059 | 723.4670 | 0.8428 | 635.4309 | 853.9572 | 0.8134 |
| SVR | 1352.5391 | 1503.4896 | 0.6309 | 1662.2470 | 1751.1622 | 0.5932 |
Table 8.
The prediction results using the data in Ohio
| Model | Training | Testing | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | R2 | MAE | RMSE | R2 | |
|
LSTM-based DA-RNN |
779.2359 | 1015.8341 | 0.9993 | 954.3849 | 1342.0370 | 0.9156 |
|
GRU-based DA-RNN |
699.2269 | 932.7992 | 0.9994 | 909.3970 | 1134.3039 | 0.9130 |
| Encoder-Decoder | 939.3892 | 1237.9832 | 0.8128 | 1049.2895 | 1689.3498 | 0.7496 |
| SVR | 1437.604 | 2038.3557 | 0.6781 | 1704.4902 | 2368.9732 | 0.5810 |
Table 9.
The prediction results using the data in Los Angeles
| Model | Training | Testing | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | R2 | MAE | RMSE | R2 | |
|
LSTM-based DA-RNN |
935.5827 | 1148.7093 | 0.9994 | 1148.3849 | 1347.3209 | 0.9837 |
|
GRU-based DA-RNN |
857.4780 | 1058.3201 | 0.9994 | 1049.1987 | 1230.2390 | 0.9810 |
| Encoder-Decoder | 1829.1779 | 2270.9733 | 0.7176 | 2029.1921 | 2346.2892 | 0.6744 |
| SVR | 2159.8801 | 2454.7972 | 0.6767 | 2126.2587 | 2587.6133 | 0.6089 |
As shown in Tables 7, 8 and 9, the results of DA-RNN with different recurrent cells both outperform those of the encoder-decoder network and SVR, which proves that the attention mechanism of DA-RNN is effective in this case. Further, the result of GRU-based DA-RNN performs slightly better than that of the LSTM-based DA-RNN. Figure 7 shows the iterative process of the loss function during the raining process of GRU-based DA-RNN. Figure 8 shows the comparison of the predicted value and the true value.
Fig. 7.
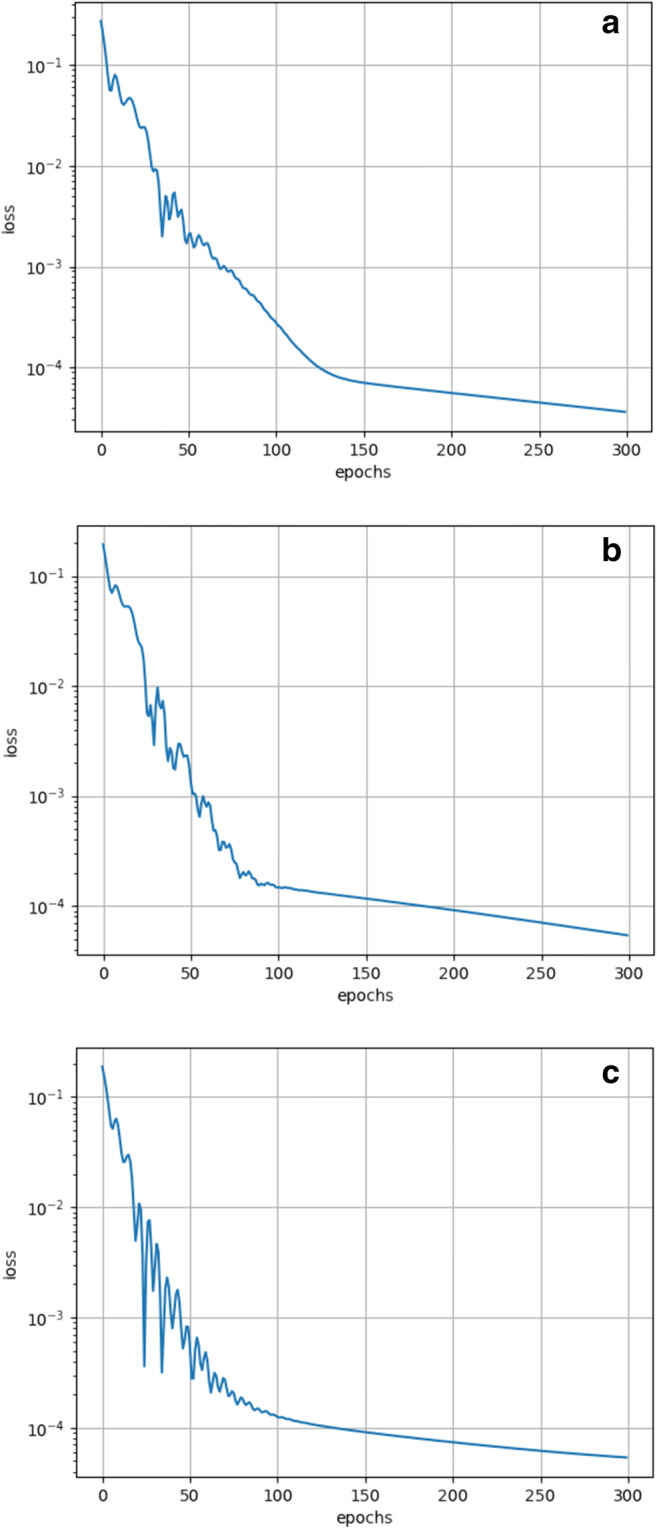
The iterative process of loss function during the training process of GRU-based DA-RNN on three different states. (a) Washington (b) Ohio (c) Los Angeles
Fig. 8.
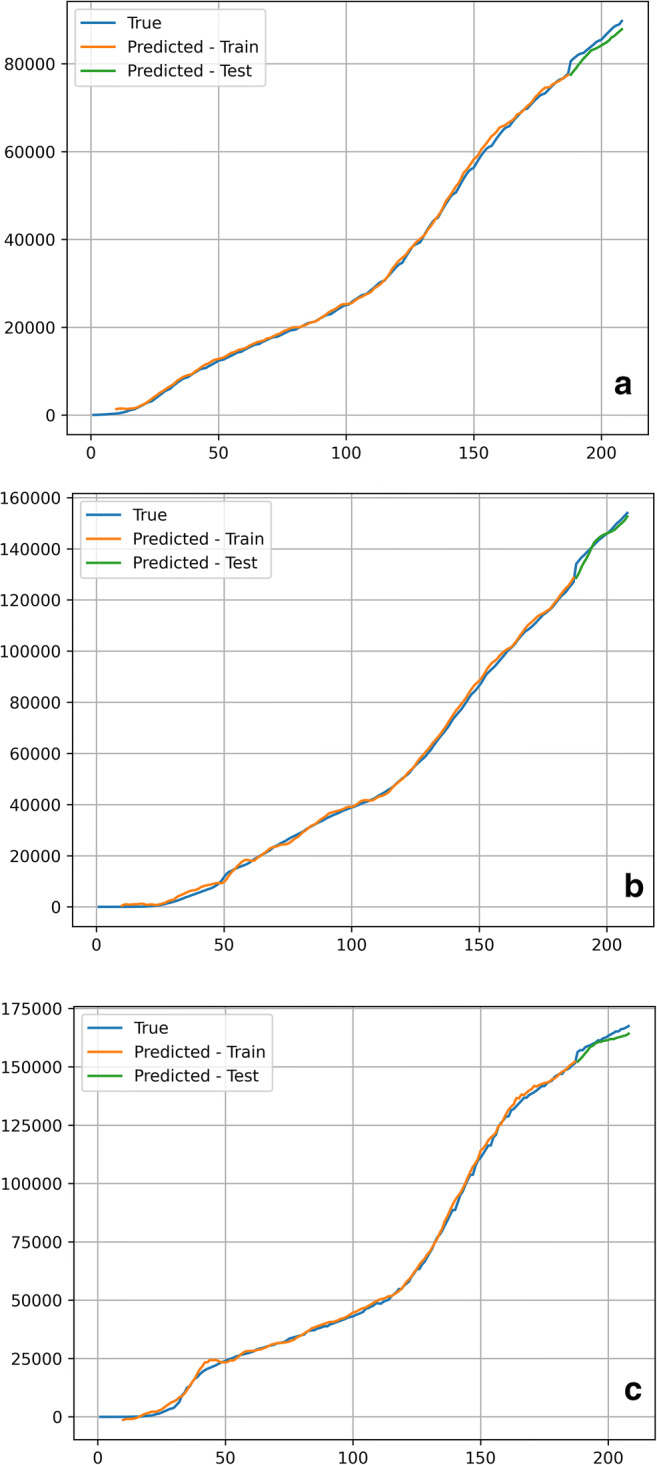
The comparison of the predicted and true values employing GRU-based DA-RNN on three different states. (a) Washington (b) Ohio (c) Los Angeles
As shown in Figs. 7 and 8, the prediction results of the GRU-based DA-RNN are very close to the true values of confirmed cases, and the loss function can converge with the normalized error less than 1 × 10−4. While more detailed data is needed to make more accurate predictions, the proposed model of this study could help to forecast future confirmed cases, as long as the spread of the COVID-19 virus does not change vastly against expectation based on historical data. Otherwise, variation characteristic may affect the spread rate and seriousness of COVID-19, and further the reliability and accuracy of the forecasting model.
Conclusion
The COVID-19 has resulted in high mortality worldwide. Researchers have built many pandemic models based on limited data and they often focus on analyzing the spread path itself and the impact of the pandemic. Nonetheless, many geographic and local factors are as well crucial to the forecasts of confirmed COVID-19 cases in certain regions. In this study, we considered both daily time-series data of confirmed cases and regional attributes in the United States as important features. Subsequently, we conducted a cross-sectional analysis and data-driven forecasting on this pandemic. The main findings of this study can be concluded as two parts:
We selected a set of influential factors that might affect the spread rate of COVID-19. XGB and SHAP were incorporated to quantify the importance static features and RF, LGB are comparable feature selectors. Through the experimental results, the most important three factors are temperature, age 65+ and pollution.
We applied GRU-based DA-RNN and LSTM-based DA-RNN to forecast the number of the confirmed COVID-19 cases for certain states in the United States. The superiority of DA-RNN was demonstrated in comparison to baseline methods including SVR and the encoder-decoder network.
Notice that, virus variation may greatly affect the spread rate and seriousness of COVID-19, and further the accuracy of the forecasting model. In future, we will consider more characteristics (e.g. the incubation period, pathogenesis, symptoms, diagnosis, etc.) from COVID-19 itself.
Acknowledgements
We are grateful to the anonymous referees of the journal for their extremely useful suggestions to improve the quality of the article.
Dr. Nan Jing
is an Associate Professor of Information Management at the Shanghai University, P.R. China, at the SHU-UTS SILC Business School. Hereceived the B.S. degree in Computer Science from Beijing University in 2000 and the M.S and Ph.D. degree in Computer Science in University of SouthernCalifornia in 2003 and 2009. His current research interests include deep learning and data mining.

Appendix
Table 10.
Sources of data used in this study
Author’s contributions
Nan Jing: Supervision, Conceptualization, Writing - Reviewing and Editing.
Zijing Shi: Methodology, Formal analysis, Software, Validation, Visualization.
Yi Hu: Data curation, Investigation, Writing - Original draft preparation.
Ji Yuan: Methodology, Validation, Writing - Reviewing and Editing.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Availability of data and material
We shared raw data at Mendeley to encourage further research.
Shi, Zijing (2021), “Raw data for COVID-19 forecasting”, Mendeley Data, V5, doi: 10.17632/6r4z88wh9h.4
Code availability
Code generated or used during the study are available from the corresponding author by request.
Declarations
Conflicts of interest/competing interests
The authors declare that they have no conflict of interest.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Chan JFW, Yuan S, Kok KH, To KKW, Chu H, Yang J, Xing F, Liu J, Yip CCY, Poon RWS, Tsoi HW, Lo SKF, Chan KH, Poon VKM, Chan WM, Ip JD, Cai JP, Cheng VCC, Chen H, Hui CKM, Yuen KY. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395:514–523. doi: 10.1016/S0140-6736(20)30154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huang C, Wang Y, Li X, Ren L, Zhao J, Hu Y, Zhang L, Fan G, Xu J, Gu X, Cheng Z, Yu T, Xia J, Wei Y, Wu W, Xie X, Yin W, Li H, Liu M, Xiao Y, Gao H, Guo L, Xie J, Wang G, Jiang R, Gao Z, Jin Q, Wang J, Cao B. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395:497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jayaweera M, Perera H, Gunawardana B, Manatunge J. Transmission of COVID-19 virus by droplets and aerosols: a critical review on the unresolved dichotomy. Environ Res. 2020;188:109819. doi: 10.1016/j.envres.2020.109819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Carelli P. A physicist ' s approach to COVID-19 transmission via expiratory droplets. Med Hypotheses. 2020;144:109997. doi: 10.1016/j.mehy.2020.109997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lotfi M, Hamblin MR, Rezaei N. COVID-19: transmission, prevention, and potential therapeutic opportunities. Clin Chim Acta. 2020;508:254–266. doi: 10.1016/j.cca.2020.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang JC, Wang SB, Xue YD. Fecal specimen diagnosis 2019 novel coronavirus–infected pneumonia. J Med Virol. 2020;92:680–682. doi: 10.1002/jmv.25742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Doremalen N, Bushmaker T, Morris DH, et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N Engl J Med. 2020;382:1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu T, Gong D, Xiao J, Hu J, He G, Rong Z, Ma W. Cluster infections play important roles in the rapid evolution of COVID-19 transmission: a systematic review. Int J Infect Dis. 2020;99:374–380. doi: 10.1016/j.ijid.2020.07.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hemmes JH, Winkler KC, Kool SM. Virus survival as a seasonal factor in influenza and poliomyelitis. Nature. 1960;188:430–431. doi: 10.1038/188430a0. [DOI] [PubMed] [Google Scholar]
- 10.Dalziel BD, Kissler S, Gog JR, Viboud C, Bjornstad O, Metcalf CJE, Grenfel BT. Urbanization and humidity shape the intensity of influenza epidemics in U.S. cities. Science. 2018;362:75–79. doi: 10.1126/science.aat6030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shrivastav LK, Jha SK. A gradient boosting machine learning approach in modeling the impact of temperature and humidity on the transmission rate of COVID-19 in India. Appl Intell. 2021;51:2727–2739. doi: 10.1007/s10489-020-01997-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wu Y, Jing W, Liu J, Ma Q, Yuan J, Wang Y, Du M, Liu M. Effects of temperature and humidity on the daily new cases and new deaths of COVID-19 in 166 countries. Sci Total Environ. 2020;729:139051. doi: 10.1016/j.scitotenv.2020.139051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhu Y, Xie J, Huang F, Cao L. Association between short-term exposure to air pollution and COVID-19 infection: evidence from China. Sci Total Environ. 2020;727:138704. doi: 10.1016/j.scitotenv.2020.138704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berman JD, Ebisu K. Changes in U.S. air pollution during the COVID-19 pandemic. Sci Total Environ. 2020;739:139864. doi: 10.1016/j.scitotenv.2020.139864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kraemer MUG, Yang CH, Gutierrez B, Wu CH, Klein B, Pigott DM, Open COVID-19 Data Working Group†. du Plessis L, Faria NR, Li R, Hanage WP, Brownstein JS, Layan M, Vespignani A, Tian H, Dye C, Pybus OG, Scarpino SV. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science. 2020;368:eabb4218. doi: 10.1126/science.abb4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maier BF, Brockmann D. Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science. 2020;368:742–746. doi: 10.1126/science.abb4557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sun J, He WT, Wang L, Lai A, Ji X, Zhai X, Li G, Suchard MA, Tian J, Zhou J, Veit M, Su S. COVID-19: epidemiology, evolution, and cross-disciplinary perspectives. Trends Mol Med. 2020;26:483–495. doi: 10.1016/j.molmed.2020.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Acter T, Uddin N, Das J, Akhter A, Choudhury TR, Kim S. Evolution of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) as coronavirus disease 2019 (COVID-19) pandemic: a global health emergency. Sci Total Environ. 2020;730:138996. doi: 10.1016/j.scitotenv.2020.138996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hernandez-Matamoros A, Fujita H, Hayashi T, Perez-Meana H. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl Soft Comput. 2020;96:106610. doi: 10.1016/j.asoc.2020.106610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jia JS, Lu X, Yuan Y, Xu G, Jia J, Christakis NA. Population flow drives Spatio-temporal distribution of COVID-19 in China. Nature. 2020;582:389–394. doi: 10.1038/s41586-020-2284-y. [DOI] [PubMed] [Google Scholar]
- 21.Ghosh K, Sengupta N, Manna D, De SK. Inter-state transmission potential and vulnerability of COVID-19 in India. Prog Disaster Sci. 2020;7:100114. doi: 10.1016/j.pdisas.2020.100114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ndairou F, Area I, Nieto JJ, Torres DF. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos, Solitons Fractals. 2020;135:109846. doi: 10.1016/j.chaos.2020.109846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Towers S, Vogt Geisse K, Zheng Y, Feng Z. Antiviral treatment for pandemic influenza: assessing potential repercussions using a seasonally forced SIR model. J Theor Biol. 2011;289:259–268. doi: 10.1016/j.jtbi.2011.08.011. [DOI] [PubMed] [Google Scholar]
- 24.Huang X, Glements ACA, Williams G, Mengersen K, Tong S, Hu W. Bayesian estimation of the dynamics of pandemic (H1N1) 2009 influenza transmission in Queensland: a space–time SIR-based model. Environ Res. 2016;146:308–314. doi: 10.1016/j.envres.2016.01.013. [DOI] [PubMed] [Google Scholar]
- 25.Huang B, Zhu Y, Gao Y, Zeng G, Zhang J, Liu J, Liu L. The analysis of isolation measures for epidemic control of COVID-19. Appl Intell. 2021;51:3074–3085. doi: 10.1007/s10489-021-02239-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kirbas I, Sozen A, Tuncer AD, Kazancioglu FS. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos, Solitons Fractals. 2020;138:110015. doi: 10.1016/j.chaos.2020.110015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nawaz MS, Fournier-Viger P, Shojaee A, Fujita H. Using artificial intelligence techniques for COVID-19 genome analysis. Appl Intell. 2021;51:3086–3103. doi: 10.1007/s10489-021-02193-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Abir M, Nelson C, Chan E, Al-Ibrahim H, Cutter C, Patel K, Bogart A (2020) Critical care surge response strategies for the 2020 COVID-19 outbreak in the United States. RAND Corporation, Santa Monica, Calif. https://www.rand.org/content/dam/rand/pubs/research_reports/RRA100/RRA164-1/RAND_RRA1 64-1.pdf. Accessed 18 August 2020
- 29.The COVID Tracking Project (2020) https://covidtracking.com/data
- 30.Chowell G, Mizumoto K. The COVID-19 pandemic in the USA: what might we expect? Lancet. 2020;395:1093–1094. doi: 10.1016/S0140-6736(20)30743-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen T, Guestrin C (2016) Xgboost: a scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 10.1145/2939672.2939785
- 32.Lundberg SM, Nair B, Vavilala MS, Horibe M, Eisses MJ, Adams T, Liston DE, Low DK, Newman SF, Kim J, Lee SI. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat Biomed Eng. 2018;2:749–760. doi: 10.1038/s41551-018-0304-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qin Y, Song D, Chen H et al (2017) A dual-stage attention-based recurrent neural network for time series prediction. Proc 26th Int Joint Conf Artif Intell 2627-2633
- 34.Ma Y, Zhao Y, Liu J, He X, Wang B, Fu S, Yan J, Niu J, Zhou J, Luo B. Effects of temperature variation and humidity on the death of COVID-19 in Wuhan, China. Sci Total Environ. 2020;724:138226. doi: 10.1016/j.scitotenv.2020.138226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Qiu Y, Chen X, Shi W. Impacts of social and economic factors on the transmission of coronavirus disease 2019 (COVID-19) in China. J Popul Econ. 2020;33:1127–1172. doi: 10.1007/s00148-020-00778-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Adekunle IA, Onanuga AT, Akinola OO, Ogunbanjo OW. Modelling spatial variations of coronavirus disease (COVID-19) in Africa. Sci Total Environ. 2020;729:138998. doi: 10.1016/j.scitotenv.2020.138998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kerimray A, Baimatova N, Ibragimova OP, Bukenov B, Kenessov B, Plotitsyn P, Karaca F. Assessing air quality changes in large cities during COVID-19 lockdowns: the impacts of traffic-free urban conditions in Almaty, Kazakhstan. Sci Total Environ. 2020;730:139179. doi: 10.1016/j.scitotenv.2020.139179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang Z, Huang Y, Cai B, Ma R, Wang Z. Stock turnover prediction using search engine data. J Circuit Syst Comp. 2021;30:2150122. doi: 10.1142/S021812662150122X. [DOI] [Google Scholar]
- 39.Lundberg S, Lee SI (2017) A unified approach to interpreting model predictions. Advances in neural information processing systems 4768–4777
- 40.Cawley GC, Talbot NLC. Preventing over-fitting during model selection via Bayesian regularisation of the hyper-parameters. J Mach Learn Res. 2007;8:841–861. doi: 10.1007/s10846-006-9125-6. [DOI] [Google Scholar]
- 41.Wang Z, Huang Y, He B, Luo T, Wang Y, Fu Y. Short-term infectious diarrhea prediction using weather and search data in Xiamen, China. Sci Program. 2020;5:1–12. doi: 10.1155/2020/8814222. [DOI] [Google Scholar]
- 42.Wang Z, Huang Y, He B (2020) Dual-grained representation for hand, foot, and mouth disease prediction within public health cyber-physical systems. Softw Pract Exper 1-16. 10.1002/spe.2940
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
We shared raw data at Mendeley to encourage further research.
Shi, Zijing (2021), “Raw data for COVID-19 forecasting”, Mendeley Data, V5, doi: 10.17632/6r4z88wh9h.4
Code generated or used during the study are available from the corresponding author by request.