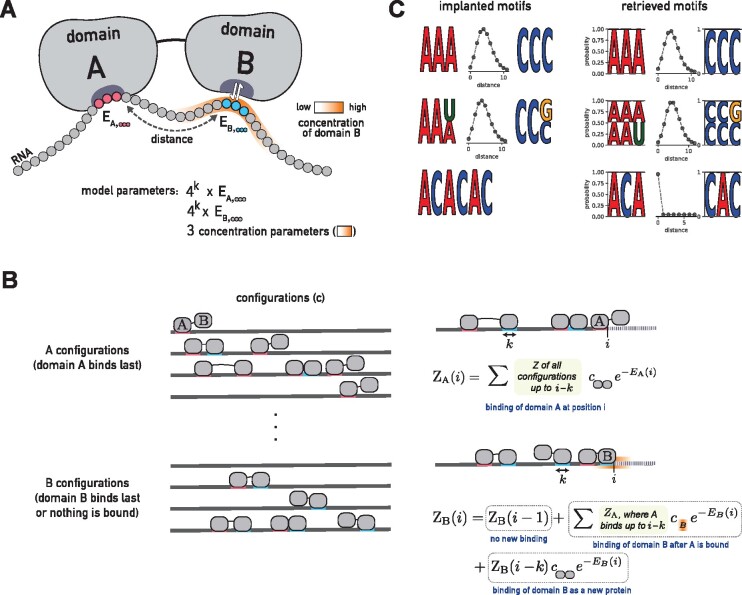
Fig. 1.

BMF can learn multivalent binding preferences for RBPs. (A) RBP-RNA interaction model for a protein with two RBDs. BMF optimizes the binding energies of each domain to all possible RNA k-mers (k = 3 here) and learns the distance distribution between the motif cores. BMF models the high RNA local concentration at the second binding site, when the first domain is bound to the RNA. (B) BMF calculates binding probabilities for all binding configurations of one or several proteins to the RNA sequence. $Z_{\mathrm{A}}(i)$ is the sum of statistical weights of all binding configurations on the RNA up to position i, for which domain A is bound at position i. Similarly, $Z_{\mathrm{B}}(i)$ is the sum of statistical weights of all binding configurations on the RNA subsequence for which no domain is bound or domain B is bound with its right edge upstream of or at position i. $Z_{\mathrm{A}}$ and $Z_{\mathrm{B}}$ are calculated iteratively (right panel). The first term in the second equation accounts for configurations for which position i is not bound by anything, the second term accounts for configurations for which domain A of the same protein is bound at j (as seen in the example illustration) and the last term accounts for configurations for which domain B binds whose A domain is not bound upstream of i. (C) BMF recovers the correct RNA motifs implanted in synthetic datasets for all tested cases. Here and in the following figures, the two learned core motifs are visualized by plotting the energies of the top five k-mers, converted to k-mer probabilities according to Boltzmann’s law and normalized to 1