Easing or tightening control strategies: determination of COVID-19 parameters for an agent-based model

Abstract

Some agent-based models have been developed to estimate the spread progression of coronavirus disease 2019 (COVID-19) and to evaluate strategies aimed to control the outbreak of the infectious disease. Nonetheless, COVID-19 parameter estimation methods are limited to observational epidemiologic studies which are essentially aggregated models. We propose a mathematical structure to determine parameters of agent-based models accounting for the mutual effects of parameters. We then use the agent-based model to assess the extent to which different control strategies can intervene the transmission of COVID-19. Easing social distancing restrictions, opening businesses, speed of enforcing control strategies, quarantining family members of isolated cases on the disease progression and encouraging the use of facemask are the strategies assessed in this study. We estimate the social distancing compliance level in Sydney greater metropolitan area and then elaborate the consequences of moderating the compliance level in the disease suppression. We also show that social distancing and facemask usage are complementary and discuss their interactive effects in detail.

Introduction

Coronavirus disease 2019 (COVID-19) first emerged in Wuhan, China in December 2019 and is an ongoing pandemic caused by Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2). China implemented intense quarantine and social distancing and full lockdown of the cities in Hubei province on January 23rd with the aim of controlling the pandemic, which has resulted into more than 81,000 reported cases until mid 2020 (WHO Team, 2020). The disease has spread in all parts of the globe by the end of 2020. Control strategies of testing, tracing and lockdowns or other social distancing have been used in many other countries successfully, whilst countries which have delayed on lockdowns have had more severe epidemics. While the policies are effective and the pandemic has been largely controlled within China, the intense quarantine and full lockdown come with huge human and economic cost, which may not be acceptable in all countries. On the other hand, relaxing the restrictions can worsen the strain on the health care systems and threaten societies by resurgence of infection.

Enhanced surveillance and testing, case isolation, contact tracing and quarantine, social distancing, facemask use, case isolation, household quarantine, teleworking, travel bans, closing businesses, and school closure are the most common strategies implemented worldwide for slowing down infection spread. While many of the strategies are currently in place in many countries, governments are looking for best policies for easing or lifting the control strategies. Thus, the extent to which restrictions can be lifted so that the disease remains under control and the economies do not suffer significant damage is a critical question.

While conventional mathematical modelling of disease spread has a long history of providing solid foundations for understanding disease dynamics, the models are sometimes aggregated, with usually detailed heterogeneities dismissed. These heterogeneities may include zone population size and density, population age structure, age-specific mixing, the size and composition of households, and critically, travel and activity participation patterns which may have important impacts on epidemic dynamics and on the effectiveness of possible interventions (Grefenstette et al., 2013). Recently, the development of disaggregated agent-based models in infectious disease epidemiology has received considerable attention owing to their capability to capture the dynamics of disease spread combined with heterogeneous mixing and social networks of agents. Agent-based models are known to better reflect the behaviour of people and the system as a whole. Further, the diversity of policies and strategies that can be assessed using agent-based models is larger than their aggregate counterparts. Teleworking, for instance, may shift agents to participate in other activities or school closure may affect the activity patterns of all the household members. We use a large-scale agent-based model to consider the dynamics of COVID-19 transmission in the Sydney greater metropolitan area (Sydney GMA), Australia.

Furthermore, the virologic and epidemiologic characteristics of SARS-CoV-2, including transmissibility and mortality, are not yet fully known. Despite a surge of efforts to estimate the disease spread parameters, they typically show considerable variations from one study to another. Their methodologies also are only applicable to aggregated models such as susceptible–infected–resistant (SIR) based models. To the best of our knowledge, there are no guidelines or research on the parameter estimation of pandemic diseases modelling in agent-based models, mainly due to the complexity of agent-based models and the existence of many interactive parameters. This paper contributes to the determination of COVID-19-specific parameters of agent-based modelling of disease spread. Further, of the few prior attempts to calibrate such parameters (Chang et al., 2020; Rockett et al., 2020; Hoertel et al., 2020), these efforts have been unstructured in that the interconnections among the parameters on the pandemic effects are not considered. Unstructured calibration refers to the sequential adjustments of parameters in a relatively ad hoc and non-systematic way. Although an unstructured calibration approach may reproduce observed statistics, the approach can be problematic for many reasons, including the failure to consider interactions among parameters, and excessive focus on observations’ replication, at the possible sacrifice of model system validity. As the first contribution of this paper, we use the response surface methodology (RSM) to efficiently transfer, adjust and calibrate the model while considering the interactions of their constituent parameters. By optimally calibrating parameters, their unbiased impacts on disease spread can be captured. Given the observed statistics, including the number of cases and public transport (PT) usage after lockdown, we calibrate the parameters for an agent-based model for the Sydney GMA. It is noteworthy to say that the transport agent-based model of Sydney includes the actual transport network with models reflecting the overall travelling behaviour of people in an urban metropolitan area.

After calibration of the transmission model parameters, we illustrate the benefits of an agent-based model in capturing the ground truth of how agents interact and their impact in shaping the system level response to several policies including the influences of easing social distancing restrictions, opening up businesses, timing of control strategies implementation, using facemask and quarantining family members of isolated cases to intervene the disease progression (as the second contribution). The intent is to provide guidance to the public health community worldwide to consider easing of restrictions using behavioural epidemiology models. It should be noted that we present marginal benefits of several containment strategies not the absolute magnitude of the benefits using our model which reflects, like all models, part of the ground truth. Also, we do not envision forecasting the future in this paper; instead, we introduce a tool or an approach to examine the effectiveness of hypothetical strategies which are impossible to be tested in the real world. All in all, while several agent-based models have been recently developed in the literature for disease spread simulations, i.e. Chang et al. (2020) and Rockett et al. (2020), the current paper is unique in 1) the use of a fully agent-based model which includes the real traffic network and activity scheduler for household agents (TASHA) and 2) the use of a structured method for model calibration.

Agent-based disease spread modelling

This section briefly explains the agent-based model used to model the pandemic spread and then, the methodology for model parameter calibration is introduced.

Related works

Deciding on appropriate control strategies among a wide range of possible alternatives is difficult; computer modelling is an invaluable tool for exploring the effects of various control strategies. Agent-based models are a class of computational models that provide a high-resolution—both temporal and spatial—representation of the epidemic at the individual level (Truszkowska et al., 2021; Kretzschmar et al., 2021). Agent-based models cover the sociodemographic attributes of people and attempt to reproduce the travel decisions and activity participations of people (Najmi et al., 2018). The use of the models has been recently surged to investigate the impact of non-pharmaceutical interventions for COVID-19.

Several agent-based models have been developed to simulate the spread of COVID-19 and evaluates the effectiveness of having various control strategies in place; the strategies include social distancing (Chang et al., 2020; Najmi et al., 2021), school closure (Chang et al., 2020; Truszkowska et al., 2021), facemask usage (Najmi et al., 2021; Müller et al., 2021), contact tracing (Aleta et al., 2020; Kerr et al., 2020), quarantining family members of isolated cases (Kerr et al., 2020; Chang et al., 2020), superspreading (Lau et al., 2020), and lockdown (Chang et al., 2020; Truszkowska et al., 2021). The agent-based models are developed for various locations including Australia (Chang et al., 2020), Singapore (Koo et al., 2020), the United States (Chao et al., 2020), and the United Kingdom (Ferguson et al., 2020). Features of these models include the simulation of in-home and out-of-home contacts (Chao et al., 2020; Kretzschmar et al., 2021; Kucharski et al., 2020), activity participation of agents (Chang et al., 2020; Müller et al., 2021), activity chains (Müller et al., 2021), and travel networks (Najmi et al., 2021). Our disease transmission model in this paper covers all the features and attempts to investigate effectiveness of the above-mentioned control strategies, except the school closure, in the Sydney GMA.

Although the merits of agent-based models have shed light on technical complexities of their implementation as well as their scalability across scenarios (Keskinocak et al., 2020), their implementation is data hungry and costly. One of the complexities relates to the calibration of the models. The studies on agent-based disease spread models in the literature are either silent on how the calibration of the models have been performed (e.g. Perez and Dragicevic, 2009; Lau et al., 2020; Kretzschmar et al., 2020; Kucharski et al., 2020), or they have explicitly mentioned that the model parameters are calibrated in an ad-hoc and non-systematic ways, solely for the purpose of fitting the results to the observed data (e.g. Chang et al., 2020; Müller et al., 2021; Gaudou et al., 2020; Truszkowska et al., 2021). The agent-based models are large scale and highly non-convex, with many interactive parameters. Building COVID-19 spread simulators on top of the agent-based model further increases the complexity. The existence of non-linearities, the lack of closed form formulations for agent-based models and the existence of many interactive parameters make the system severely under-determined. Therefore, numerous sets of parameters can be found for the parameters such that the model reproduces the observed statistics. While there are many estimations for the parameters in observational epidemiologic studies in the literature, there is no study that systematically generates parameters for the agent-based models. Systematic calibration of an agent-based disease spread model is a key contribution of the current paper.

SydneyGMA model

The agent-based disease transmission model (ABDSM; Najmi, 2020) in this paper is coded in Python and built on an agent-based model developed for the Sydney GMA, called SydneyGMA, which has several properties that are valuable for analysing the effectiveness of COVID-19 control strategies. Firstly, SydneyGMA uses the Travel/Activity Scheduler for Household Agents (TASHA), an operational, state-of-the-art model of daily travel and out-of-home activity participation that considers both individual activities as well as joint household activities, along with a full range of within-household interactions (Miller and Roorda, 2003; Miller et al., 2005; Roorda and Miller, 2006; Roorda et al., 2008, 2009Travel Management Group, 2020). In addition to Sydney, TASHA has been applied in Toronto, Canada, where it is the operational model for Toronto transportation planning agencies (Miller et al., 2016), Finland (Birdsey et al., 2019), and Temuco, Chile. All parameters of the Toronto model are transferred to the Sydney model. Consequently, in the case of school closures or widespread working from home, the activities of households will be realistically rescheduled, factoring in the extra time derived from removing school- and work-related activities from the household's regular schedule. Secondly, mode choice is computed for each household individually, and interactions between household members using their vehicle on individual or joint trips are captured, as well their usage of other modes of travel, notably transit. Thirdly, the model “assigns” transit (PT) trips to explicit paths through the transit network, enabling different components of transit trips (including in-vehicle, walking to/from transit, and waiting and transferring) to be estimated and considered as potential situations for disease spread. Therefore, utilising the SydneyGMA augments the disease spread modelling by accounting for potential locations of disease spread and more accurately modelling interactions among household members as a result of adjustments to their daily activities. Appendix 1explains more details on SydneyGMA. Note that the population size in SydneyGMA is about 5.8 million.

Disease spread parameter calibration

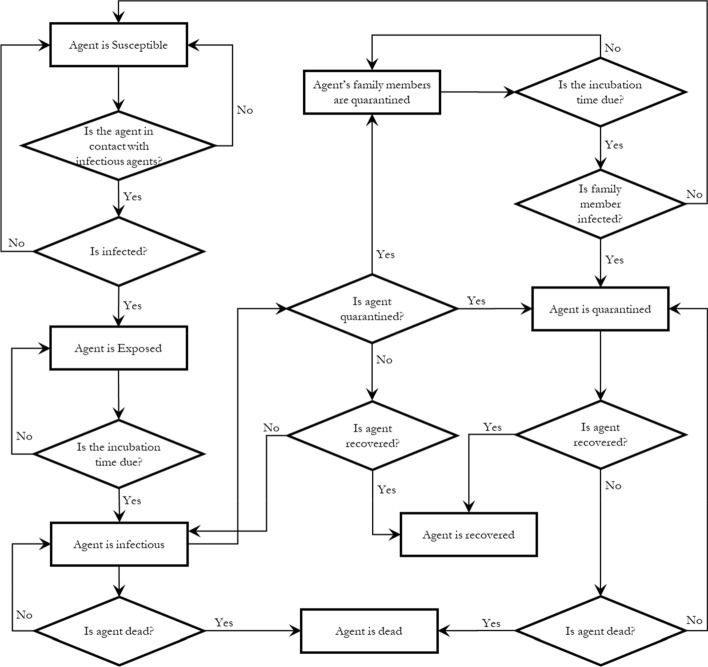
While SydneyGMA is originally developed to simulate the travel behavior of people, it is extended to model the transmission of the disease in the population while the people participate various activities including work and school and use different modes. We call the extension agent-based disease spread model which is built on SydneyGMA to simulate the spread of the disease over the social network (see Fig. 1). In the agent-based disease spread model, a disease spread simulator frequently runs SydneyGMA. Similar to the other agent-based models, the SydneyGMA is for daily travel scheduling while the agent-based disease spread model should cover the whole lifetime of pandemic which may be few months or years. The disease spread simulator, explained in Appendix 2, iteratively interacts with SydneyGMA model once per day and scrutinises the itinerary of each agent in the system. To illustrate more, the time-step is a day in which the disease state of each agent is updated. The changes in the states affect the travel behaviour and activity participation of each agent (and their family members itineraries) in subsequent days of the simulation.

Fig. 1.

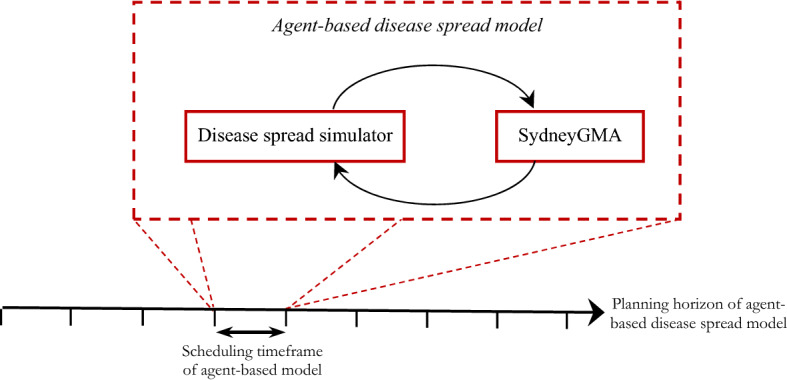
The structure of agent-based disease spread models

There are several factors that affect the movement rates (probabilities) among the different disease states. The factors can be categorised into (1) travel behaviour-specific parameters, (2) disease-specific parameters, and (3) policy-specific parameters. The travel behaviour-specific parameters affect out-of-home activity participation rates, destination choices, travel mode choices, the start time, location and duration of out-of-home activity episodes, and contact number for activity type. Except for the contact number, the other parameters are transferred from the original TASHA model and adjusted for the Sydney context and integrated to the transport network of Sydney.

The disease-specific parameters include incubation period, average time required for an infected agent to recover, and the probabilities of: becoming infected (per contacted person), transitioning from infectious to quarantined (per day), infected agents dying (per day), and transitioning from quarantined to recovered (per day). In Appendix 3, we describe the parameter calibration procedure used to determine the parameters for the agent-based disease spread models and present the resulting calibrated parameters in Table 2. The parameter calibration procedure is based on previously published work by Najmi et al. (2020).

Table 2.

Calibrated parameters

Parameters	Lower bound	Upper bound	Desirability function	Calibrated value
Base infection probability (per trip)	0.03	0.05		0.044
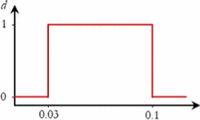
Infection probability at home (per day per case)	0.03	0.1		0.052
Correction factor of infection probability of individuals with manufacturing, professional and other occupations compared to general and sale occupations	1	1.5		1.26
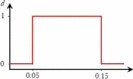
Quarantine probability (per day)	0.05	0.15		0.12
SD compliance level after lockdown	60%	100%		85.94%
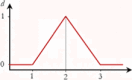
Base contact number (per trip)	1	3		2
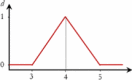
Incubation period	3	6		4.93
Base contact number in PT vehicle	6	14		13.85

The strategy-specific parameters determine the policies that might be applied by policymakers and authorities to slow down disease spread. These include, but are not limited to, the enforcement of business closings, teleworking, and, if applicable, easing the restrictions on businesses; school closures and re-openings; infected case isolation; quarantining of family members; social distancing, facemask use; and the dates when the restrictions are in place. Of these, variations in school closure strategy have not been considered in this paper due to the huge uncertainty that exists with respect to the impact of the virus on children. Another strategy-specific parameter is the change of trip generation rates, which is usually ignored in conventional disease spreading models.

Control strategies

We evaluate several control strategies, namely: home quarantine of family members of the traced infected cases, social distancing, travel load reduction, facemask usage, and the date when the control strategies are imposed. Different scenarios are run to explore these control strategies and the dates when they are implemented. However, we do not explore the impact of case isolation (CI) and school closure (SC) in this paper. CI and SC strategies are set to our best estimate of current values for the Sydney GMA and are held constant across all experiments. We assume that CI is implemented from the start day of the epidemic, as has been the case in Australia and most other countries. The SC strategy comes into effect in the analysis in the week starting 23 March 2020. Early in this week, the schools were still open, but it was up to parents to decide whether to send their children to school or not. Thus, SC is considered to remove schools and universities from the list of activities for a majority of students. We assume that universities are partially open and 10% of university students continue to travel to universities in this scenario. Obviously, the SC affects the daily travel itinerary of the students and their family members. Studies have estimated that SC requires around 15% of the workforce to take time off work to care for children, which is associated with considerable costs (Scott, 2020). This changes in the activity participation is captured by SydneyGMA.

Scenario assumptions for each of the control strategies examined are briefly described in each of the following sub-sections.

Quarantined family members (QF)

QF is a common strategy to control pandemics. While different levels of quarantine strategies are implemented worldwide, we only investigate the existence or the lack of this strategy. In the case of existence, we assume that the strategy is implemented from the day of finding the first case in New South Wales (NSW), on 22 January 2020. Following identification of a symptomatic case in a household, all household members remain at home for 14 days.

Social distancing (SD)

SD is a key parameter in disease transmission models and affects the rate at which sick people infect susceptible people; it refers to the extra care of people, to reserve extra distance from others, compared to the normal conditions (with zero SD). Thus, SD compliance of 0 does not mean that people are in full contact. We impose SD in our model by the adjustment of all non-household contacts (referred to as compliance level) while the intra-household contacts are kept unchanged which is in line with the pandemic studies of Chang et al. (2020) and Ferguson et al. (2020). Thus, the SD compliance levels may vary from zero-SD – no compliance- to full lockdown-full compliance, with a rate at which the contact rates are affected following the SD control strategy. This strategy came into effect in NSW on 31 March 2020. Note that the SD compliance level is assumed to be the same, however, it is assumed to be variable and unknown everywhere in the system such as within the public transport system and in regarding the activities of participations.

Travel load (TL)

TL addresses trip cancellations and is used to reduce non-essential trips, including leisure, sport, and religious activities. Also, it includes the reduction in trips due to teleworking, layoffs, and quitting a job. Similar to SD, we define different levels and investigate the influence of enforcement to eliminate unnecessary trips. We consider the TL level in Sydney GMA in April 2020 as the extreme level in our investigations and explore the influences of easing the restrictions. Despite some rare cases, as in Wuhan, where the TL levels have approached 0%, in many other countries, the enforcement of the severe TL restrictions is impossible. The TL strategy comes into effect within the analysis starting from 23 March 2020.

Facemask usage (FU)

Recently, FU is highly emphasised to reduce the chance of getting infected while participating in different outdoor activities. Different values of the facemask efficiency have been reported in the literature but almost all of them use odd ratio (e.g. Chu et al., 2020 and Schünemann et al., 2020). The model in the current paper needs the per contact efficiency of facemask as the paper uses an agent-based approach which simulates the interaction among agents. The per contact efficiency has not been reported in the literature and the possibility of using the OR estimations for the per contact efficiency is under debate. Therefore, we consider different values of 0.6, 0.7, 0.8, and 0.9 for the per contact facemask efficiency to address the ambiguity that exists for the per contact efficiency of facemask. We use these efficiencies in the infection rate of those agents that use mask while participating activities out of home. We assume that nobody wear mask at home. Similar to SD, we define different levels and investigate the influence of different levels of facemask usage while participating activities out of home. The FU level may vary between 0%—nobody wears mask- to 100%—everybody wear mask. In this paper we evaluate the disease spread at six FU levels of 0%, 20%, 40%, 60%, 80% and 100% for investigation.

Date of lockdown (DL)

The date when the control strategies are implemented is a controversial decision for authorities. This is a difficult decision for governments, as it has detrimental effects on economies and, in the worst case, might result in economic collapse.

It should be noted that an important effect of lockdowns is on travel behaviour, and, as a result, on urban travel demand. There is no current data that provide information about the changes in travel decisions of agents after lockdown. Thus, we need to make some assumptions, the most important of which is the travel volume after lockdown. As there is no reliable data on the generated trips after lockdown in Sydney GMA (in April 2020) compared to before, we assumed 50% reductions in the total number of trips for calibration purposes. However, according to Transport for NSW (2020), the PT usage reduced by 79% after lockdown. Thus, the change in the PT usage is a piece of reliable information we used and adjusted the utility of PT mode in SydneyGMA to fit the simulated ratio to the observed statistic.

The next section explores the effects of implementing and relaxing each of these control strategies.

Runs and results

As the system is probabilistic, starting with very small number of infected cases (e.g. one or two cases) may substantially affect the simulation results, depending on whether the model quarantine them sooner or later. Thus, we use an initial set of four infected cases in the population. Because there have been four active cases in Sydney GMA on 28 February 2020, this date is selected as the starting point of experiments. The calibrated agent-based disease spread model is used for policy analysis; the simulation results are presented and discussed in the following subsections. Each of the simulations is run three times to account for the randomness in the agent-based model where the averages of the evaluation measures are plotted.

Base case

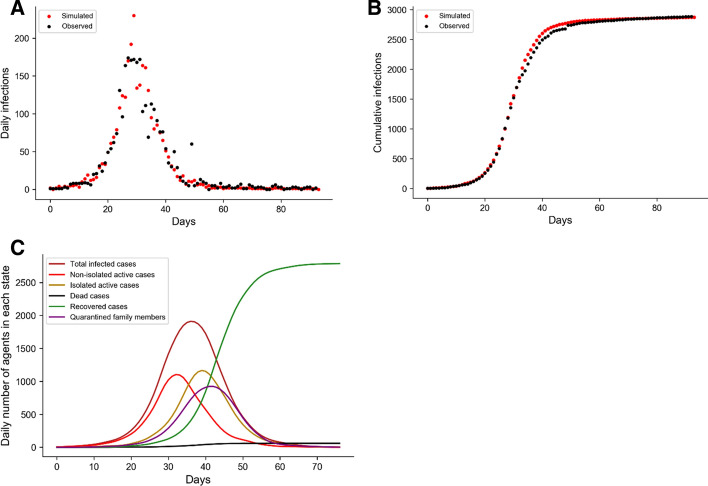
The base case scenario is equivalent to the settings that reproduce the observed statistics; thus, it is the output of the calibration model. Figure 2 shows the base case scenario obtained from the simulation of the ongoing spread of COVID-19 and reproduces the disease spread progression in SydneyGMA. In the scenario, all the control strategies are in place as observed in NSW. The SD compliance level and TL level strategies after lockdown are determined and considered at 85.9% (this value is determined by the calibration model), called the base SD compliance level, and 50%, called the base TL level, respectively (see Appendix 3). Figure 2(a) and (b) reveal the high performance of our calibrated disease transmission model in reproducing the observed infected cases. As a result of the restrictions implemented by the Australian government in the last week of March 2020, the infection rate drops sharply, and the epidemic almost dies out. Figure 2(c) shows the simulation result of running the model in the base scenario. This figure distinguishes between the isolated (but not necessarily infectious) and non-isolated cases. Thus, the model estimates that about half of the persons in quarantined state are the family members that are not actually infected. In reality, while family members of infected cases are quarantined, their infection to the disease has not yet been determined.

Fig. 2.

Power of the calibrated SydneyGMA -based disease spreading model in reproducing the daily number of cases a, the cumulative number of cases b and the number of cases at each state of the pandemic modelling c in the base-case scenario

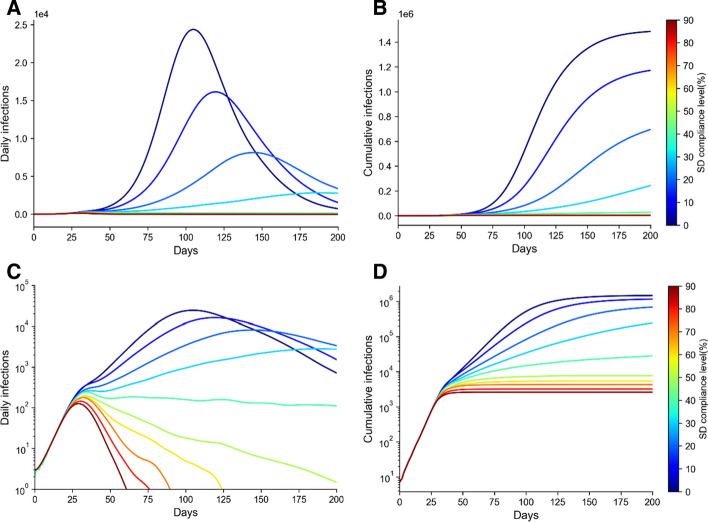
Various SD compliances

In the model calibration, we found the base SD compliance level after the shutdown in the Sydney GMA. However, the exploration of easing the compliance level on the disease distribution allows policymakers to identify the minimum compliance levels for which the disease might be controlled. Figure 3 shows the simulation results of the social distancing strategies, coupled with QF and base TL level, across different compliance levels. We do not consider the SD compliance level of 100% as it is almost impossible to achieve. The figure reveals that compliance levels of less than 70% do not show enough strength to suppress the disease within 3 months. At these compliance levels, the number of emerging new cases is higher than the potential of the health system to find and isolate the infected cases. While the SD base compliance level could eliminate the disease, or hold it close to zero cases, in about 2 months, the lower SD compliance levels of 80% and 70% could control the disease with a delay of 14 and 28 days respectively. Reducing the SD compliance by 15.9%, from 85.9% to 70%, can increase the cumulative number of cases by 59%. Still, this is much better than the scenario in which there is 50% or less SD compliance level in place.

Fig. 3.

A comparison of different SD compliance levels. The settings for other control strategies are the same as in the base scenario. a daily number of cases (linear), b cumulative cases (linear), c daily number of cases (logarithmic), and d cumulative cases (logarithmic). Note: Responding to the skewness of large values, (A) and (B) are plotted in logarithmic scale in (C) and (D)

The compliance levels between 50 and 60% are still effective in reducing the infected cases (at base TL level), but they do not suppress the disease in a short period of time. Thus, control of the disease with these SD levels required a longer time period. In these cases, the resurgence of disease spreading is probable. The SD compliances levels of less than 50% are not strong enough, for any duration, to suppress the disease.

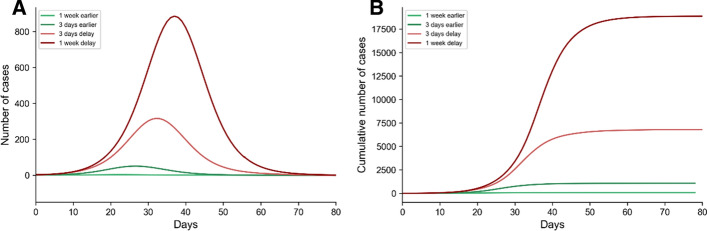
Speed of implementation of lockdown

We evaluate the timing of the implementation of lockdown in Sydney GMA. Figure 4 explores the scenarios where all the control strategy settings are the same as in the base case scenario, but they are enforced either 3 or 7 days earlier or later than the actual introduction date. This figure reveals the impact of selecting an appropriate time to apply the control strategies. Left unchecked, the spread of the disease grows exponentially such that in the first three weeks the number of infected agents is small, and the situation does not seem dramatic. Then, the values change rapidly. Earlier enforcement could lead to 96% and 63% fewer cases for the scenarios with the lockdown implemented 7 and 3 days sooner, respectively. The delays of 3 and 7 days, on the other hand, could lead to, respectively, 130% and 570% increases in the number of cases. A week’s delay not only increases the pressure on the health system considerably but also requires an approximately 30-day longer suppression period.

Fig. 4.

A comparison between the influence of implementing the lockdown earlier (in greenish) and later (in reddish) while all the strategies are in place as in the base case scenario. a Daily number of cases, and b Cumulative number of cases

Opening businesses

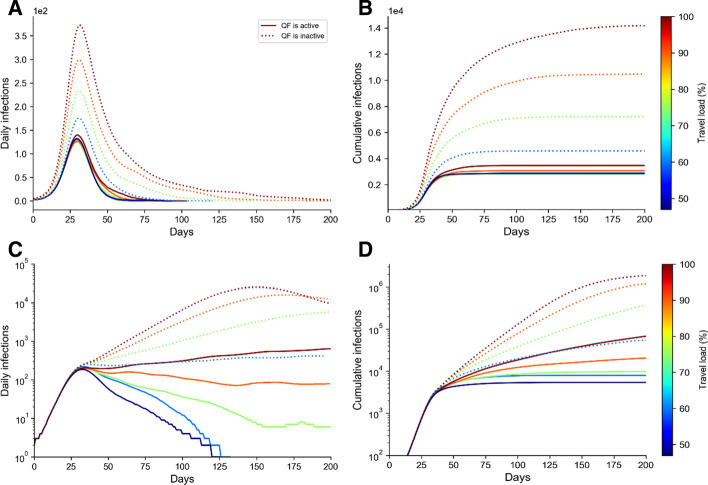
In the base scenario, we defined the base SD compliance and base TL levels. Furthermore, in Fig. 3, we showed that compliance levels over 60% can suppress the disease in a reasonable time (at the base TL level). Suppose that the generated trips increase by easing the restrictions on businesses to open again, but all other in-place strategies are still in effect. To examine this case, we run the model with different TL levels across both the base and 60% SD compliance levels to investigate the interaction effect of the SD and TL control strategies. The results of running the scenarios are presented in Fig. 5. The figure also explores the importance of the QF control strategy in controlling the disease spread.

Fig. 5.

A comparison of different travel load and its interaction with home quarantine strategy at two social distance compliance levels of 85.9% and 60%. a daily number of cases at the SD compliance level of 85.9%, b cumulative cases daily number of cases at the SD compliance level of 85.9%, c daily number of cases at the SD compliance level of 60%, and (D) cumulative cases daily number of cases at the SD compliance level of 60%. Note: Responding to the skewness of large values, (C) and (D) are plotted in logarithmic scale

Having the QF strategy in place throughout the period, the base SD compliance is very successful in controlling the disease spread progression in a short period of time for all the TL levels. However, while the SD compliance level of 60% can be successful in suppressing the base travel load, the result is may not satisfactory for travel loads of 80% and over. This reveals that even slightly easing the social distance controls while the travel demand is close to the pre-COVID-19 travel demand level, may be ineffective.

The figure also shows that relaxing the QF control strategy significantly increases the disease suppressing period, even if a high compliance level of social distancing is in place. Further, relaxing the QF multiplies the number of patients. It also remarkably increases the magnitude of the daily infections, especially when coupled with a low SD compliance level. Thus, the QF strategy has significant interaction effects on both travel load and SD compliance level, such that ignoring the QF strategy multiplies the daily infection rate and infected cases. Note that few of the plots in Fig. 5 are for scenarios with high SD compliance level of 85.9% and high travel loads. It should be emphasised that the scenarios are model fictions, and improbable to be achieved in reality.

Wearing facemask

While many of the control strategies are currently in place in many countries, the continuation of enforcing some of these strategies (e.g. travel ban, school closure, and lockdown) for a long time is impractical. The continuation of these strategies may have detrimental effects on the economy, some irreversible and in the worst case, might result in an economic collapse. Thus, this section assumes TL is at the same level as before COVID-19 (almost 100%) when all the agents participate in their activities, including work, school attendance, recreational activities etc., freely (unless they are in quarantined); and analyses the influence of the facemask usage and its interaction with social distancing on controlling the disease transmission.

The starting point at which the FU and SD are imposed, including the daily number of infections and cumulative infections, may influence the performance of the control strategies. To address this issue and to better evaluate the performance of the facemask usage scenarios in controlling the disease transmission, we impose the use of facemask and complying the SD at different starting conditions provided in Table 1. In line with this, we allow agents in the system to progressively get infected without enforcing SD and FU control strategies. Given three different starting points, we impose the FU and SD control strategies. For example, at the starting point of 2 at which we apply the SD and FU control strategies, the daily and cumulative infections reach 108 and 699 cases. The average of the simulation results under the three starting points has been used to analyse the facemask efficiency.

Table 1.

starting points of different random streams for facemask analysis

Initial conditions	Daily infections	Cumulative infections
Starting point 1	11	73
Starting point 2	108	699
Starting point 3	1,040	7,975

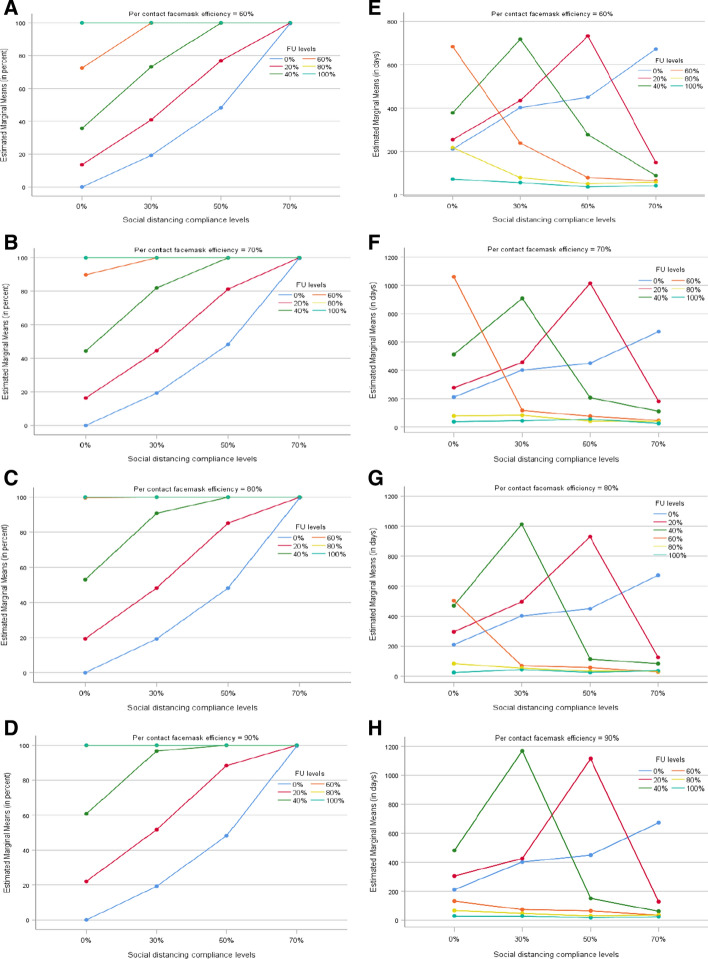
The interactions of SD and FU control strategies are evaluated in terms of 1) reduction rate in the number of infections (Fig. 6a-d) and 2) the time it takes the disease spread getting under control (Fig. 6e-h) across different values of per contact facemask efficiencies. Note that to better understanding the development of infections, another representation of this figure is provided in Appendix 4. In Fig. 6, the estimated marginal means across different starting points are plotted. In analysing the figures, three matters should be considered. First, the SD compliance level of 70% is less likely to happen when the TL is almost 100%. Second, the percentages of reduction in Fig. 6 are obtained by comparing the number of infections obtained at different SD and FU levels with a scenario where no SD and FU control strategies (both the SD and FU levels are 0%) are in place. For better understanding of the meaning of one percent reduction in the number of infections, it is worth mentioning that the scenario with no SD and FU strategies generates about 3.75 million infections; this value is equivalent to 65% of population which lies within the range reported in Anderson et al. (2020a, b). Thus, one percent reduction corresponds to about 37.5 thousand infections. Third, the absolute values on y-axis of Fig. 6e-h should not be analysed as it is sensitive to the initial starting points; instead, the sensitivity of the results to the changes in the SD and FU levels are the key attributes that we seek for.

Fig. 6.

A comparison of different levels of wearing facemask, at different per contact efficiencies, and their interactions with social distancing levels when the TL is the same as pre-COVID. a-d The reduction rate in the number of infections at different per contact efficiencies, e–h The time it takes the disease spread getting under control at different per contact efficiencies

Figure 6a–d reveal several intuitive results. First, the SD and FU strategies are fully complementary in reducing the number of infections so that the negligence in undertaking one of them can be compensated by using the other one. Second, higher facemask efficiency plays a more effective role in high compliance levels of FU compared to the lower levels of FU. For example, while the facemask efficiency of 90% is 28% more efficient than the facemask efficiency of 60%, in increasing the reduction rate in the number of infections, at the FU compliance level of 60%. However, this value is only 8% at the FU compliance level of 20%. Third, across all the per contact facemask efficiencies, the 0% and 20% of facemask usage rates are not sufficient to keep the number of cases low, unless the SD compliance level is high, at the 70%, which is less likely to happen. At the SD compliance level of 50%, the FU level of 20% does also reduce the number of cases significantly but it may still put pressure on the health system. The FU levels of 40% and higher have promising performances at the SD levels of at least 50% across different facemask efficiencies. Fourth, the number of infections shows a significant sensitivity to the lower values of SD and FU control strategies. In contrast, the sensitivity reduces by increasing the SD and FU levels. The figure also shows that wearing masks by over 80% of people can be a conservative solution for opening up the economy. At these levels, the number of infections shows the lowest sensitivity to the facemask efficiency and SD compliance level. This is a plausible strategy for opening the economy owing to the fact that making the facemask usage a mandatory rule and controlling people’s compliance to the rule is much easier than enforcing social distancing. Social distancing is a fuzzy concept, and its compliance is at most a behavioral requirement which is not to a large extent controllable by local authorities. In contrast, the facemask usage is a binary concept of yes/no; thus, controlling and penalising people who avoid using facemask should be a convenient solution controlled by enforcement aiming at full implementation.

Figure 6e-h reveal that the times to control the disease transmission has the highest interactive effect at the FU levels 20% and 40% where the time it takes to control the disease highly depends on the SD level. The FU levels of 20% and 40% show a non-monotonic behaviour. At these levels, the society reaches the herd immunisation and supresses the virus at the low and high SD compliance levels, respectively. In both the cases, the virus is eliminated earlier than the situations where the FU level is about 20% or 40% with a moderate SD compliance level. The FU levels of 0% has an increasing trend meaning that increasing the SD compliance level postpones the herd immunisation achievement. In contrast, the FU levels of 80% and 100% have a decreasing trend meaning that the higher SD compliance levels supress the virus earlier. FU level of 60% shows a high sensitivity to the facemask efficiency and SD compliance level. At the SD level of 0% and the facemask efficiencies of less than 80%, FU level of 60% takes a long time to control the disease; the reason is that the infection rate that the society experiences is neither high enough to reach the early herd immunisation nor low enough to supress the virus. At a higher level of any of the facemask efficiency or SD compliance levels, 60% can be a sufficient FU level to control the disease.

Conclusion

NSW had the largest number of cases, and the greatest challenges in disease control. This paper presented a behavioural agent-based model for modelling the actual mobility of Sydney residents where interactions of agents, their travel trajectory and system level attributes such as traffic condition on different modes of transport are captured. Using the extremely high resolution of activities in the system, we were able to measure marginal costs and benefits of hypothetical conditions of the system and people. We could simulate situations with different levels such as the compliance profile of people in response to different containment policies which is impossible otherwise if not having a simulation tool like ours. To establish a reliable foundation for the sensitivity analysis, we calibrated our agent-based model to match what was observed in NSW during the lockdown. Then we assessed numerous combinations of levels of various well-known policies such as social distancing, travelling limitations, facemask usage, and full lockdown. Our proposed bottom-up modelling framework unleashes the power of high computing capacity for policy appraisal without requiring any discounts or limits on modelling how people behave in the system.

We showed that to open up again, on a backdrop of low disease incidence, mitigating resurgence of COVID-19 and maintaining the hard-won gains was critical. We estimated that the likely compliance with social distancing was 85.9% during the period of lockdown in Sydney GMA, and that reduction in compliance could result in disease resurgence. As society re-opens, enhanced surveillance and testing for COVID-19 is essential, and at the first signal of resurgence, lockdown should be implemented without delay. We also showed that a delay of even 1 week can be costly. A return to normal travel and use of public transport in Sydney GMA will result in a risk of resurgence but can be mitigated. We also discussed that the use of facemasks can be key to safer resumption of travel within Sydney.

We admit that the agent-based models like ours are data hungry to be calibrated, however we position ourselves in the literature alongside others argued that huge assumptions about the performance of aggregate models are not less harmful than data and computational requirements of disaggregate agent-based models. Nonetheless, each of these modelling paradigms have huge advantages to offer, so we aimed at presenting the benefits of the agent-based modelling scheme which is relatively overlooked for modelling pandemic situations. Also, this paper attempted to calibrate disease spread parameters specific to agent-based models. Other research studies can use the calibrated parameters while developing their agent-based disease spread models and then adjust the parameters if required.

Biographies

Ali Najmi

is a Research Associate at the research Centre for Integrated Transport Innovation (rCITI) at the University of New South Wales (UNSW). He holds a Ph.D. from UNSW, a Master of Science degree in Socio-economics Engineering and a Bachelor of Science in Industrial Engineering from the Iran University of Science and Technology (IUST), Iran. His research focus on calibration of different types of transport models including four-step models, Activity-based models, market equilibrium and supernetworks.

Sahar Nazari

is currently a Research Assistant at UNSW. She obtained her Bachelor of Science degree from IUST, Iran and has nine years of professional research and industrial experience, including laboratory manager and lead of product development research team at Techenomics Australia (research and engineering company).

Farshid Safarighouzhdi

is a Research Associate at rCITI, UNSW. Farshid holds a Bachelor of Engineering in Civil Engineering from Azad University, Iran, a Master of Science in Civil Engineering (Transport) from the Sharif University of Technology, Tehran, Iran, and a Ph.D. in Transportation Engineering from the IUST, Tehran, Iran. His key research interests include large-scale transport network modelling and transport network design, activity-based travel demand modelling, travel behaviour analysis under uncertainty, urban data analytics, and microsimulation modelling for urban mobility.

Eric J. Miller

is Director of the University of Toronto Transportation Research Institute. He has Bachelor of Science and Master of Science degrees from the University of Toronto and a Ph.D. from M.I.T. Research interests include integrated land use transportation modelling, agent-based microsimulation and sustainable transportation planning.

Raina MacIntyre

is NHMRC Principal Research Fellow and Professor of Global Biosecurity. She heads the Biosecurity Program at the Kirby Institute, which conducts research in epidemiology, vaccinology, bioterrorism prevention, mathematical modelling, genetic epidemiology, public health and clinical trials in infectious diseases. Her research falls under 4 areas: Personal protective equipment, Vaccinology, Epidemic response and emerging infectious diseases, and Bioterrorism prevention. She is a dual-specialist physician with training in epidemiology and modelling. She is best known for research in the detailed understanding of the transmission dynamics and prevention of infectious diseases, particularly respiratory pathogens such as influenza, tuberculosis, bioterrorism agents and vaccine-preventable infections.

Taha H. Rashidi

is a Senior Lecturer of Transportation Engineering in the School of Civil and Environmental Engineering at UNSW. He holds a Ph.D. degree from the University of Illinois at Chicago (UIC) and a Master of Science degree from Sharif University of Technology, Iran. He is a member of the Transportation Research Board (TRB) Committee on Traveler Behavior and Values (ADB10). Dr. Rashidi was bestowed the Fred Burggraf Award from Transportation Research Board (TRB) of the National Academies in 2008. He was the Dwight David Eisenhower Transportation Fellow in 2008. He also received American Society of Civil Engineers Freeman Fellowship in 2009. More recently in 2012, Dr. Rashidi was twice recognized by the National Science and Engineering Research Council (NSERC), Canada, which bestowed on him the NSERC PDF Award and the Industrial RAND Fellowship. During his tenure at UNSW, Dr. Rashidi was awarded the Early Career Research Grant from the Faculty of Engineering.

Appendix 1: Agent-based Model of SydneyGMA

SydneyGMA, similar to many other agent-based models, is large-scale with many interactive models which are iteratively solved until convergence. The models can be categorised into three main components of population synthesiser, travel demand, and network. The population synthesiser in the SydneyGMA generates the whole population and families. Population synthesiser uses an iterative proportional fitting (IPF) method on the data from Australian Bureau of Statistics. It synthesised individual characteristics (such as age, gender, driving licence, transit pass, employment status, occupation, free parking, student status, employment zone, school zone) and family attributes (such as number of members, number of vehicles, dwelling type) for all 5.8 million Sydney residents.

In SydneyGMA, the travel demand component has various models including a scheduler, so-called TASHA, and several choice models. TASHA is an agent-based microsimulation and household-based model and builds a person’s activity schedule from the bottom-up, beginning with the generation of individual and multi-person activity episodes, and entering those activities into a feasible activity schedule, shifting and shortening activities as necessary to resolve situations where activities overlap in time. Trip chains arise naturally out of this process, and TASHA includes a tour-based mode choice model that explicitly evaluates ridesharing, vehicle allocation and joint travel to joint activities. Choice models simulate activities and travel behaviours based on the characteristics of individuals, their families and travel patterns in the city. As the description of each of these models is out of the scope of this appendix, their description has been omitted. The interested readers can refer to Miller and Roorda (2003), Roorda et al. (2008), or Travel Management Group (2020) for further information. Travel times are the determining factors in all the choice models in the demand component. Travel times are estimated using the network component. In the network component, the travel time is determined by assigning the travel demand to different routes in the road network. After determining the travel times over various links of the network, the demand estimation model is iterated, and this process continues until convergence where the travel times of successive iterations reach to the predefined criterion.

In a nutshell, the SydneyGMA simulates the activities of all the people living in Sydney GMA. In addition to the socio-economic characteristics of each person, SydneyGMA determines the details of each person's activities such as purpose, start and end time of each activity, place of activity and travel mode. Owing to such information, i.e. the interaction of people, which is the main factor of disease spread in communities, can be simulated as the tempo-spatial information of all the people is known. Thus, the SydneyGMA model is used in this study to build an agent-based disease spread model to provide rigorous evaluation of various control strategies.

Similar to every other model, SydneyGMA has several limitations. First, SydneyGMA is developed by transferring GTAModel V4.1, which is originally developed for Greater Toronto-Hamilton Area (GTHA). Transferring is a common approach in developing agent-based models because there is no immediate need for re-estimation of parameters (Bowman et al., 2014; Castiglione et al., 2014). While the socioeconomic data, network datafiles and procedures for Sydney has been used for the development of SydneyGMA, there are still some parameters that need to be estimated and replaced. As the paper objective is to investigate different control strategies comparatively, we believe that being at this stage of transferring does not affect our scenario analysis remarkably. Second, SydneyGMA incorporates all the travel and out-of-home activity participation decisions and household profiles of each agent, it is not able to explicitly model out-of-home interactions among agents at a micro “fact-to-face” level. While the model generates the activity type and the zone where an agent participates in an out-of-home activity, it does not provide detailed information about other agents who have been in contact with this agent at the specific activity location (e.g., a store) at the specific time of the agent’s visit to this location. Thus, we had randomly pick interacting agents from those who were in the same zone and activity level and overlap at the attendance time. The same assumption has been used for the PT mode. Third, the SydneyGMA does not provide the specific PT vehicle that is used by each agent. Thus, we select interacting agents from those that use the PT mode to get to the same destination and activity type with approaching times that are close to each other. Assumptions made about the transport model do not affect the conclusions drawn from the relative analysis conducted in Sect. Runs and results section, as the intention of the paper is not to provide accurate forecasts, instead it is aimed to assess the relative costs and benefits of different conferment policies.

Appendix 2: Proposed disease transmission model

The proposed disease transmission model is built on the SydneyGMA activity/travel agent-based microsimulation model. It stochastically models disease transmission due to inter-agent interactions while travelling and engaging in out-of-home activities, as well as within-household interactions. It sensitive to a wide range of disease control strategies affecting these interactions Seven classes of agents are included in the transmission model: (1) Susceptible agents (S), who are not in contact with infectious agents and are subject to be infected, (2) Exposed agents, who are infected agents but in the incubation period (latent) of the disease, (3) Infectious agents, who are contagious, (4) Quarantined agents, who are infected agents quarantined by health care authorities, (5) Quarantined family members, who are the family members of at least one infected and quarantined agent, (6) Dead agents, who are the infected persons, either in quarantine or not, that have died, and (7) Recovered agents, who are infected persons, either in quarantine or not, who have recovered.

Figure 7 presents flow chart which explains in detail the sequence of the states in the proposed model. Firstly, all agents, except those who are infectious, are susceptible. The susceptible agents may come into contact with contagious agents and then may acquire the infection probabilistically and move to the exposed state. Exposed agents remain non-contagious for a given incubation period. In our simulation, the incubation period is a parameter that should be calibrated. At the end of the incubation period, agents will become contagious and move into the infectious class. Infectious agents, both symptomatic and asymptomatic cases, become quarantined by health care authorities probabilistically. Thereby, they move into the quarantined class. Obviously, non-quarantined agents are the main source of disease spread in the system. Upon discovery of an infected agent, not only does the health care authority quarantine them, but they also quarantine their family members as they have a high chance of being exposed to the disease and may be in their incubation period. The quarantined family members who are infected will move into the Quarantine class. Quarantined agents may respond to treatment and recover, and move to recovered class, or die, and move to the dead class. Albeit, for COVID-19, infected but non-quarantined agents have also a small chance to die and move to the dead class, but we ignore this possibility in this paper. On recovery from infection, individuals are assumed to be immunised. All the infected agents, either quarantined or not, will be recovered after 14 days which is the typical recovery period of COVID-19.

Fig. 7.

Disease spread simulator

Appendix 3: Model calibration approach

Parameters of disease transmission models including contact rate and infection rate are interconnected and their influences are complementary. The agent-based disease transmission models (including disease spreading models and agent-based models) are highly non-convex, so a reliable mathematical model between the parameters (called dependent factors) and their effects (called responses of interest) are not available. We use a response surface methodology (RSM) to calibrate the disease transmission model. RSM consists of a set of mathematical and statistical techniques used to develop, improve and optimise processes in which a response of interest is influenced by several factors, with the eventual objective of optimising the response (Box and Draper, 2007). Therefore, RSM quantifies the functional relationship between a response of interest, $y$, and the explanatory factors, $x$ (See Eq. 1). This mathematical representation may correspond to different orders of polynomial functions (Najmi et al., 2020). In this paper, we choose the order of polynomial corner points of each equation based on a fitness function value for the estimated equations. It should be emphasised that the interaction of the parameters can also be estimated mathematically. For a complete review of RSM techniques, the reader is referred to Khuri and Mukhopadhyay (2010).

$$y=f\left(x_1,x_2,\dots ,x_m\right)$$ 1

RSM shows how the parameters $x$ affect outputs $y$, and allows determination of the independent parameters that optimise the output for calibration purposes. To conduct an RSM analysis, we use a central composite design (CCD) to design the experiments and analyse the results to obtain the optimal parameter values. CCD was firstly introduced in Box and Wilson (1951), as the design matrix because it allows reliable identification of first-order interactions between parameters while providing a second-order polynomial model to predict their optimum levels (Myers et al., 2009). The methodology is shown in Fig. 8 for three factors. CCD uses three groups of corner points, centre points, and axial points to fit the functional relationship in Eq. 1. Corner points represent the factorial design points and are coded by $\pm 1$. In a centre point, coded as zero, the value of each factor is the median of the values used in the factorial portion. For axial points, all parameters are held constant at zero, except for one with the value of $+\alpha$ or $-\alpha$, as a design parameter (Marget, 2015). For more information about different experimental designs and the required number of experiments to be run, the reader is referred to Myers et al. (2009) and Ranade and Thiagarajan (2017). Furthermore, we refer the interested readers to Najmi et al. (2020) where an application of the CCD model to calibrate an agent-based model is discussed.

Fig. 8.

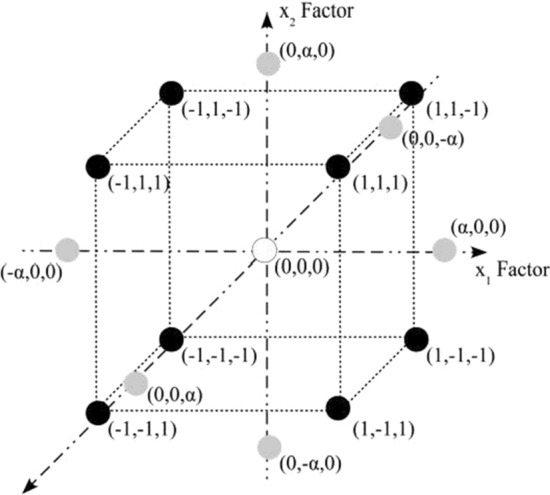
Schematic diagram of a three-factor central composite design (CCD)

Applied to the disease transmission model calibration, the factors are the parameters that should be considered for calibration and responses are the model outputs that should be reproduced. In the following paragraphs, we illustrate the parameters and model outputs that we have considered for calibration. Note that for each parameter, we define a feasible range from which its optimum value should be determined. A value is the best when its interaction with other parameters results in the best model performance (Najmi et al., 2019). Not only may the values in a feasible range not have the same probability to be selected, but also having a uniform probability for the values may generate poor results. Thus, we use values that have already been estimated in other studies for some of the parameters and penalise deviations from these values.

Different incubation periods have been reported in various studies, including 2 days in Chang et al. (2020) and 5–6 days in Anderson et al. (2020a, b). However, most of the researchers have reported the parameter to be around 4 days (Guan et al., 2020). Thus, we use 3 to 6 days for the feasible range of incubation period paramerter from which the values closer to 4.5 are considered to be more desirable and have a higher chance of being selected.

Contact intensity and contact number are important parameters in agent-based models. Recently, several studies have attempted to model the contact intensity at different location. For example, Müller et al. (2021) and Chang et al. (2020) attempt to use more precise contact intensity indicators, respectively, by integrating an air exchange rate per person and dividing the infection probability by the available floor space per person. However, for simplicity, we do not consider contact intensity in this paper as it significantly increases the calibration process. Instead, we focus on contact numbers. Recently, Prem et al. (2017) provided estimates for the contact number in different countries where the average of total out-of-home activities is around 3 to 10. As the average number of out-of-home activity trips is 2.9 in SydneyGMA, we assume that the contact number per trip for all activity types is a function of occupation and is within the range of 1 to 3. As for incubation period parameter, we assign a higher chance (and so higher desirability) to the values close to 2. This is very helpful, as it reduces the degree of freedom in the calibration of parameters. We also assume that agents with sales (including sales workers) and general (including community and personal service workers, clerical and administrative workers) occupations have higher contact rates compared to the agents with other occupation types with a coefficient placed in the range 1 to 1.5.

Contact numbers on PT vehicles is a controversial parameter. Muller et al. (2020) assume that the number is 10 times higher on PT vehicles than in activities; therefore, we consider the feasible range of 6 to 14. While some of the cases are asymptomatic with mild disease, they can be traced and isolated if they have been in contact with a household member of colleague, who is symptomatic and already isolated (Ferguson et al., 2020). Therefore, we can assume all the infected cases have the same daily probability to be traced and quarantined with a daily probability within the range of 0.05 to 0.15. The reproduction number is another parameter that recently has been frequently reported, with most of the estimations placed between 3 and 5 (Liu et al., 2020; Anastassopoulou et al., 2020). Dividing the values by the number of infectious days, average contact number and average daily number of trips results in an estimation of the feasible range for base infection probability per trip in the range of 0.03 to 0.05. Note that we do not differentiate between symptomatic and asymptomatic cases and assume that all the infected cases have the same infectious rates. Table 2summaries the selected parameters and their feasible ranges. Note that in the table, we are calibrating the base infection probability and base contact numbers. The infection probability and contact numbers in the simulations are obtained by multiplying the base contact numbers and the efficiency of using control strategies. For example, the infection probability of a scenario in which the SD compliance level is 30 percent is (1–30%) × base infection probability.

The daily and cumulative infected cases are the best-defined measures of disease spread in urban areas, with reliable data generally being publicly available (i.e. see NSW Government, 2020). According to an estimation by Price et al. (2020), the case detection rate in NSW has been 94%. Therefore, using the observed infections for calibration is reliable. We use maximise predicted fit to these two variables as the objective for parameter calibration. Furthermore, we use the simulation results in Muller et al. (2020) and assume that 23 percent of infections occur on PT vehicles, as the third objective to fit. Note that PT share of infections might be a problematic index to be used in modelling as estimating the share of infections in PT is usually unknown; different estimations may affect other parameters. Replication of death rate is another important objective to meet; however, the interaction of the death rate parameter on the model performance is not significant. Thus, the reproduction of number of death individuals can be easily met.

Once the model parameters and objective functions have been defined, experiments to explore the parameter solution spaced need to be conducted. The number of experiments and their design is a function of desired accuracy, and the number of selected parameters for calibration. For more information about experimental designs, readers are referred to Ahn (2015). We used a factorial design with a ½ fraction of a 2 ^k experiments where k is the number of parameters to be calibrated. Including the appropriate axial and centre points, a total of 145 singular experiments with different parameter settings were run. Moreover, to address the randomness in the agent-based model, each experiment was run three times with different random seeds; the averages of the evaluation measures were used for analysis. After conducting the experiments and calculating their respective response values, the functional relationships in Eq. (1) can be obtained. The next step is to use the developed functional relationships in an optimisation formulation and find the optimum values for the parameters. In other words, we seek the best combination of parameters that can reproduce the observed statistics of daily number of cases, cumulative number of cases, and proportion of infections occurring in PT. We use simultaneous optimisation using desirability functions, as popularised by Derringer and Suich (1980). In this technique, each parameter $x_i$ and response $y_j$ is converted into a desirability function ($d_i$ and $d_j$ respectively) that varies between 0 and 1. If a parameter $x_i$ is outside its feasible range, then $d_i=0$, otherwise, it receives a desirability index based on a desirability function defined for the parameter. Based on the feasible ranges and their desirabilities that we defined before, the desirability functions are generated and shown in Table 2. The same definition applies for observations and their desirability functions, except that the desirability functions are different than those for parameters. To quantify the power of the model to reproduce the observed data a function (index) is needed to measure the closeness of the simulated outputs to observed statistics. Root mean square error (RMSE) and absolute deviation are common functions used in the literature. The smaller the indexes are, the better the model fit. Thus, the target values are zero and values close to it have highest desirability (See Table 3). The design parameters are determined by solving the formulation in Eq. 2 which seeks the best combination of parameter values that maximise the overall desirability of the system (Myers et al., 2009).

$$max{\left(\prod _{i\in \left\{1..m\right\}}{d}_i\left(x_i\right)\right)}^{\frac{1}{m}}{\left(\prod _{j\in \left\{1..n\right\}}{d}_j\left(y_j\right)\right)}^{\frac{1}{n}}$$ 2

Table 3.

Objective criteria for calibration

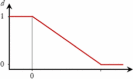
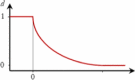
Response of interest	Evaluation criteria	Target value	Desirability function
Daily infected cases	RMSE	0
Cumulative infected cases	RMSE	0
Proportion of infections on PT vehicles	Sum of absolute deviation	0

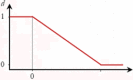
Subject to:

$$y_j=f_j\left(x_1,x_2,\dots ,x_m\right)\forall j\in \left\{1..n\right\}$$

In this equation, $m$ and $n$ are the total number of parameters and the total number of objective criteria, respectively. The interested readers are referred to Najmi et al. (2020) for detailed description about the calibration procedure. Using the simultaneous optimisation on the desirability functions the best values for the disease-specific parameters are obtained and given in the last column of Table2 . Most importantly, the calibrated value for SD compliance level after lockdown is 85.9% which means that the contact numbers have been reduced by 85.9% in Sydney GMA after lockdown. It should be mentioned that few software such as Design-Expert provide modules to solve Eq. (2) through numerical optimisation to find a point that maximises the desirability function.

Sensitivity analysis of the calibrated parameters

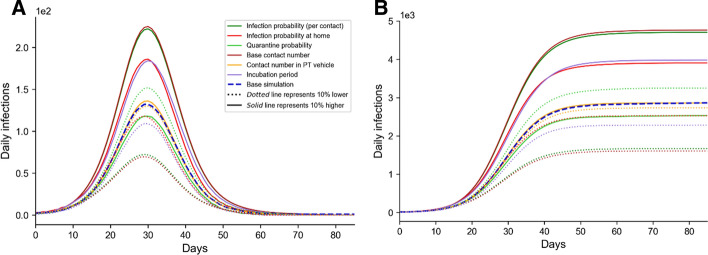
This section evaluates the sensitivity of the model to the calibrated parameters. In line with this, the parameters are fixed at their calibrated values and only one of them, in each simulation, is adjusted by 10% above and below the calibrated value. Figure 9 shows the changes in the daily and cumulative infections in each simulation. The highest sensitivities belong to the base contact number and the per contact infection probability followed by the infection probability at home, incubation period, and quarantine probability.

Fig. 9.

Sensitivity analysis of the model by adjusting different calibrated parameters by 10% above and below their calibrated values. a Daily number of cases, and b Cumulative number of cases

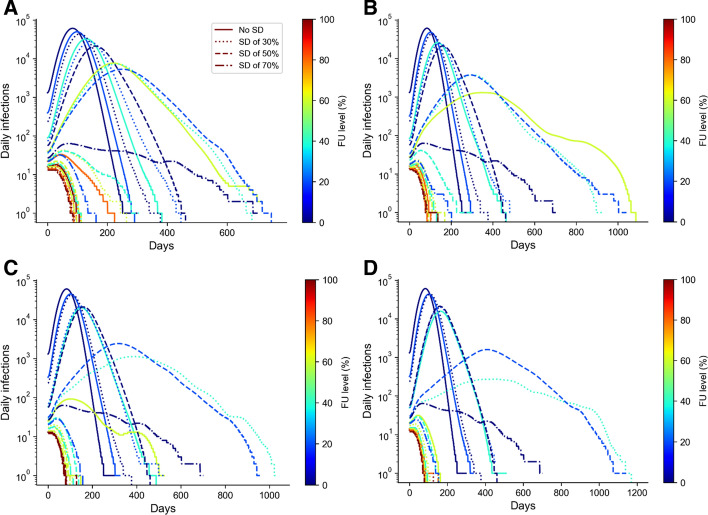
Appendix 4

Another representation of Fig. 6 is provided in Fig. 10.

Fig. 10.

Daily number of cases (logarithmic) at different FU and SD levels under per contact efficiencies of 60% a, 70% b, 80% c, and 90% d

Authors’ contribution

Ali Najmi: Literature Search and Review, Conception, Research Methodology, Model Development, Analysis, Manuscript Writing, Sahar Nazari: Model implementation, Analysis, Manuscript Writing and Editing, Farshid Safarighouzhdi: Model implementation, Manuscript Editing, Eric J. Miller: Research Methodology, Manuscript Editing, Raina MacIntyre: Research Methodology, Manuscript Editing, Taha H. Rashidi: Model Development, Conception, Research Methodology, Manuscript Editing.

Funding

The Authors did not receive any specific funding for this work.

Data availability

The daily and cumulative data which are used for the model calibration are reported in NSW Government (2020) which is already cited in the revised paper. Regarding the SydneyGMA, it has been originally developed for Toronto, Canada and then it has been transferred to few other cities worldwide. We cannot make the SydneyGMA publicly available as it is in the discretion of the inventors. Also, this model uses the EMME package for auto and transit assignment as well as estimation of travel time where EMME is not an open source software. Furthermore, we have borrowed the road and transit network of Sydney from “Transport for NSW “ organization, and we are not allowed to share it beyond the research team. Thus, we have only cited few publications discussing the development of the model. Most importantly, we have cited the webpage of the agent-based model in the revised paper (see https://tmg.utoronto.ca/doc/1.4/gtamodel/index.html).

Code availability

We have made available the code which is used for running each of the experiments on GitHub (see https://github.com/Anajmi/ABDSM/blob/main/ABDTM.py).

Declaration

Conflicts of interest

All authors have seen and approved the manuscript and have contributed significantly to the paper. Also, the authors declare that they have no conflict of interest.