A Phase I-II Basket Trial Design to Optimize Dose-Schedule Regimes Based on Delayed Outcomes

Abstract

This paper proposes a Bayesian adaptive basket trial design to optimize the dose–schedule regimes of an experimental agent within disease subtypes, called “baskets”, for phase I-II clinical trials based on late-onset efficacy and toxicity. To characterize the association among the baskets and regimes, a Bayesian hierarchical model is assumed that includes a heterogeneity parameter, adaptively updated during the trial, that quantifies information shared across baskets. To account for late-onset outcomes when doing sequential decision making, unobserved outcomes are treated as missing values and imputed by exploiting early biomarker and low-grade toxicity information. Elicited joint utilities of efficacy and toxicity are used for decision making. Patients are randomized adaptively to regimes while accounting for baskets, with randomization probabilities proportional to the posterior probability of achieving maximum utility. Simulations are presented to assess the design’s robustness and ability to identify optimal dose–schedule regimes within disease subtypes, and to compare it to a simplified design that treats the subtypes independently.

1. Introduction

Early-phase oncology clinical trials were traditionally designed to evaluate new treatments under the assumption that patients are homogeneous. Advances in cancer biology and genomic medicine have shifted the focus of cancer research and therapy from conventional chemotherapy to agents that target specific genetic or molecular abnormalities (Simon and Roychowdhury, 2013). Because different cancer histologies may share a common target, this motivates the evaluation of different cancers within the same clinical trial. To accommodate this approach in the early-phase evaluation of a new targeted agent, basket trials have emerged as a way to account for different disease subtypes (Redig and Jänne, 2015; Ornes, 2016). Basket trials provide an approach that is intermediate between conducting separate trials within cancer subtypes and ignoring subtypes entirely. Compared to traditional early-phase trial designs, a basket trial has the advantages of borrowing strength between disease subtypes, which may improve the efficiency of the trial in terms of sample size and trial duration (Simon et al., 2016), and also may allow for the inclusion of patients with rare cancers.

Several adaptive basket trial designs have been proposed. Thall et al. (2003) and Berry et al. (2013) used hierarchical models to borrow information across different cancer subtypes. Simon et al. (2016) proposed a Bayesian model that includes a parameter to quantify heterogeneity of treatment effects across disease subtypes. Cunanan et al. (2017) proposed an efficient two-stage basket trial design. Trippa and Alexander (2017) proposed using adaptive randomization (AR) in a Bayesian basket trial design. Chu and Yuan (2018a) proposed a calibrated Bayesian hierarchical model to improve performance. Chu and Yuan (2018b) proposed a Bayesian latent-class design to account for subtype heterogeneity by adaptively grouping the disease subtypes into clusters based on their treatment responses, and then borrowing information within the clusters using a Bayesian hierarchical model.

Our research is motivated by a planned phase I-II trial to optimize the (dose, schedule) regime of PGF melphalan as a single agent preparative regimen for autologous stem cell transplantation (autosct) in patients with multiple myeloma (MM). This disease is heterogeneous, with several different classification systems, studied by Zhang et al. (2006). Most commonly, MM is dichotomized as hyperdiploid or not, in terms of pathogenesis pathways defined by genetic and cytogenetic abnormalities. A review is given by Fonseca, et al. (2009). The primary objective of our motivating trial is to determine the optimal (dose, schedule) treatment regime for each MM subtype by using efficacy and toxicity as co-primary endpoints (Thall et al., 2013; Yuan, Nguyen and Thall, 2016). The trial will study three PGF melphalan doses, 200, 225 and 250 mg/m², and three infusion schedules, 30 minutes, 12 hours, and 24 hours, yielding nine treatment regimes. Toxicity is defined as the binary indicator of grade 3 mucositis lasting > 3 days or any grade 4 (severe) or 5 (fatal) non-hematologic or non-infectious toxicity, with onset within 30 days from the start of treatment infusion. In particular, a patient cannot be assessed as having “no toxicity” until he/she has been followed for 30 days. Efficacy is defined as the binary indicator of complete remission, evaluated at day 90. Thus, toxicity may be observed soon enough to feasibly apply a sequential toxicity-based decision rule, but the efficacy outcome is evaluated much later. Even if the accrual rate is moderately fast, a substantial number of treated patients will not have had their efficacy outcomes assessed, and some patients will not have had their toxicity outcomes assessed, at the time that treatment regimes must be chosen for newly enrolled patients. This is a major logistical difficulty when making outcome-adaptive decisions for new patients, including choosing (dose, schedule) or determining whether a treatment regime is unsafe. Furthermore, these adaptive decisions must be made for each MM subgroup.

In this paper, we propose an efficient basket design for adaptively optimizing dose-schedule regimes, and conducting safety monitoring, within disease subtypes in phase I-II trials with late-onset (toxicity, efficacy) outcomes. This problem has not been considered by existing methods for basket trials. In the MM trial, the design allows patients with different subtypes to be given different dose-schedule regimes, an example of “precision medicine.” In phase I-II trials with heterogeneous patients, a major concern is whether the dose–efficacy or dose-toxicity curves differ between disease subtypes. This is more complex than basing decisions on one-dimensional treatment effects, which are the basis for existing basket trial designs. Dealing with multi-dimensional outcomes is challenging in early phase trial designs. See, for example, Lee, et al. (2019).

The MM trial is complicated by the following four issues: (1) Adaptive treatment decisions must account for the relationships between efficacy, toxicity, dose, schedule, and disease subtype. (2) For each disease subtype, the Pr(efficacy | dose, schedule, subtype) function may take a variety of possible forms that may or may not be monotonic in dose. Nearly all existing subtype-specific phase I dose-finding designs assume monotonic increasing dose–toxicity curves. See, for example, Morita et al. (2017), Chapple and Thall (2018). (3) In the MM trial, because efficacy is scored at day 90 from the start of therapy, no efficacy data for patients who have been followed for less than 90 days are available, but it is not feasible to suspend accrual until all previously treated patients’ outcomes are fully observed, to apply outcome-adaptive rules. Thus, we may not use existing adaptive methods that consider only time-to-event outcomes and use follow-up time without efficacy as partial information, as in the designs of Cheung and Chappell (2000) and Yuan and Yin (2011). (4) Borrowing information across subtypes is not straightforward, because it is unknown a priori whether (dose, schedule) effects are homogeneous or heterogeneous between subtypes.

To construct a practical design that addresses all of these issues, we assume a flexible three-level Bayesian hierarchical model to characterize the associations among dose, schedule, disease subtype, and the (toxicity, efficacy) outcome. The hierarchical model facilitates borrowing information adaptively across subtypes. To improve the probability of identifying optimal (dose, schedule) regimes within subtypes, the design repeatedly determines whether or not treatment effects are homogeneous across subtypes. We treat temporarily unobserved (“late-onset”) outcomes as missing values, and impute them by exploiting auxiliary information that is observed sooner, including low-grade toxicity and bioactivity data. This substantially improves efficiency when such auxiliary outcomes are informative. Elicited utilities of (toxicity, efficacy) outcomes are used as a basis for sequentially adaptive subtype-specific (dose, schedule) optimization. To avoid getting stuck at a suboptimal regime, our proposed two-stage design adaptively randomizes each newly enrolled patient to a treatment regime according to that patient’s disease subtype.

A simpler design is proposed by Lin et al. (2019) to optimize dose–schedule regimes in a similar setting, but it assumes that the probability of treatment efficacy is strictly ordered for different subtypes, and it does not borrow any additional information to deal with delayed outcomes. In contrast, the design proposed in here is more general in that (1) it does not make any ordering assumption about the probability of efficacy, (2) it can adaptively identify response homogeneity or heterogeneity across subtypes based on the observed data, and (3) it uses more of the available data, including bioactivity and low-grade toxicity data, in making treatment decisions when some previously treated patients have efficacy outcome data pending.

To make things concrete, we present the design in the context of the motivating trial. The design potentially can be applied quite widely, however. In many early phase oncology trials, the efficacy outcome is defined to be evaluated a substantial amount of time after the start of therapy. Moreover, it is routine practice to define toxicity as an ordinal categorical variable, in terms of severity grade, and to record biological or conventional prognostic variables related to efficacy prior to enrollment.

The remainder of this paper is organized as follows. In Section 2, we present the hierarchical model for the subtype–dose–schedule–response relationship and the Bayesian data augmentation model for unobserved outcomes. In Section 3, we describe the trial design, including the utility function, rules for trial conduct, and prior elicitation methods. In Section 4, we apply the proposed design to the motivating trial and conduct simulation studies to examine the design’s performance. We close with a brief discussion in Section 5 and provide other technical details and the results of additional simulations in the Supplementary Material. The R code to implement and simulate the proposed design is available from the first author upon request.

2. Probability Model

2.1. Inference model

We consider a phase I-II trial to evaluate all combinations of D doses and S treatment schedules, for a total of DS treatment regimes, where each patient has one of B different tumor subtypes, known as “baskets.” Let n denote the number of patients accrued by an interim decision-making point in the trial, and index patients by i = 1, …, n. For the i^th patient, denote toxicity by X_i, efficacy by Y_i, cancer subtype by b_i ∈ {1, …, B}, and the assigned dose-schedule treatment regime by r_i = (d_i, s_i), for d_i ∈ {1, …, D}, and s_i ∈ {1, …, S}. We assume that X_i and Y_i both are binary, with X_i = 1 indicating dose-limiting toxicity (DLT) and Y_i = 1 indicating response. However, toxicity may occur and be observed at any time during a predefined assessment window [0, T_X] and, similarly, efficacy is either observed at some time during a window [0, T_Y] or observed at T_Y. This is similar to the outcome structures considered in a phase I-II setting by Jin et al. (2014). Extension of this structure to accommodate bivariate ordinal outcomes, as in Thall et al. (2017), is conceptually straightforward but technically much more complex.

To characterize the joint distribution of the observed outcomes (X_i, Y_i) as a function of regime r_i and disease subtype b_i, we propose a three-level Bayesian hierarchical model. This is more elaborate than a more conventional two-level hierarchical model, and is motivated by the desire to account for (1) effects of latent variables used to define the observed outcomes, done in the Level 1 model, and also (2) joint effects of patient subgroups and treatment regimes, done in the Level 2 model. This may be regarded as an extra level in the hierarchy that accounts for between-patient variability while borrowing information between subtypes by assuming that the mean (subtype, schedule) effects are iid across disease subtypes. Level 3 then provides priors for mean and variance parameters appearing in Level 2 of the hierarchical model.

Formally, following Albert and Chib (1993), Chen and Dey (1998), and Chib and Greenberg (1998), as a device to facilitate joint modeling and computation, we define each observed (X_i, Y_i) pair in terms of real-valued bivariate normal latent variables, (ξ_i, η_i), as X_i = I(ξ_i > 0) and Y_i = I(η_i > 0), where I(A) denotes the indicator function for the event A. Thus, the joint distribution of (X_i, Y_i) is induced by that of (ξ_i, η_i). The three-level hierarchical model that we use to specify the distribution of the latent variables (ξ_i, η_i), for disease subtype b_i, and treatment regime r_i = (d_i, s_i), is as follows:

$$\begin{array}{ll}\text{Level }1:\hfill & {\xi }_i\mid b_i,r_i,u_i,{\tilde{\xi }}_{b_i,r_i},{\sigma }_{\xi }^2\stackrel{\text{ind}}{~}\text{N}\left({\tilde{\xi }}_{b_i,r_i}+u_i,{\sigma }_{\xi }^2\right),i=1,\dots ,n\hfill \\ \hfill & {\eta }_i\mid b_i,r_i,v_i,{\tilde{\eta }}_{b_i,r_i},{\sigma }_{\eta }^2\stackrel{\text{ind}}{~}\text{N}\left({\tilde{\eta }}_{b_i,r_i}+v_i,{\sigma }_{\eta }^2\right),i=1,\dots ,n\hfill \\ \text{Level }2:\hfill & u_i,v_i\mid {\Sigma }_{u,v}\stackrel{\text{i.i.d.}}{~}\text{BN}\left({\mathbf{0}}_2,{\Sigma }_{u,v}\right),i=1,\dots ,n\hfill \\ \hfill & {\tilde{\xi }}_{b,r}\mid {\ddot{\xi }}_r,{\tau }_{\xi }\stackrel{\text{i.i.d.}}{~}\text{N}\left({\ddot{\xi }}_r,{\tau }_{\xi }^2\right),b=1,\dots ,B\hfill \\ \hfill & {\tilde{\eta }}_{b,r}\mid {\ddot{\eta }}_r,{\tau }_{\eta }\stackrel{\text{i.i.d.}}{~}\text{N}\left({\ddot{\eta }}_r,{\tau }_{\eta }^2\right),b=1,\dots ,B\hfill \\ \text{Level }3:\hfill & {\ddot{\xi }}_{d,s}|{\ddot{\mathit{\xi }}}_{-d,s},{\xi }_0,{\nu }_{\xi }^2\stackrel{\text{i.i.d.}}{~}\text{N}\left({\xi }_0,{\nu }_{\xi }^2\right)\text{I}\left({\ddot{\xi }}_{d-1,s}<{\ddot{\xi }}_{d,s}<{\ddot{\xi }}_{d+1,s}\right),d=1,\dots ,D\hfill \\ \hfill & {\ddot{\eta }}_{d,s}\mid {\eta }_0,{\nu }_{\eta }^2\stackrel{\text{i.i.d.}}{~}\text{N}\left({\eta }_0,{\nu }_{\eta }^2\right),d=1,\dots ,D\hfill \\ \hfill & {\tau }_{\xi },{\tau }_{\eta }\mid {\psi }_0,{\gamma }_0\stackrel{\text{ind}}{~}\text{ half-Cauchy}\left({\psi }_0,{\gamma }_0\right).\hfill \end{array}$$ (2.1)

Above, BN(0₂, Σ_u,v) denotes a bivariate normal distribution with mean vector 0₂ = (0, 0) and covariance matrix Σ_u,v, ${\ddot{\mathit{\xi }}}_{-d,s}$ denotes the subvector of ${\ddot{\mathit{\xi }}}_s=\left({\ddot{\xi }}_{1,s},\dots ,{\ddot{\xi }}_{D,s}\right)$ with ${\ddot{\xi }}_{d,s}$ deleted for d = 1, …, D, and N(·)I(A) denotes the truncated normal distribution having support given by the set A in the indicator function. We denote the vector of all fixed hyperparameters that must be prespecified by ${\theta }_0=\left({\sigma }_{\xi }^2,{\sigma }_{\eta }^2,{\Sigma }_{u,v},{\xi }_0,{\eta }_0,{\nu }_{\xi }^2,{\nu }_{\eta }^2,{\psi }_0,{\gamma }_0\right)$.

In Level 1 of the model, the patient-specific random effects (u_i, v_i) induce association between ξ_i and η_i, which in turn induces the association between X_i and Y_i. Numerical values of the hyperparameters $\left({\sigma }_{\xi }^2,{\sigma }_{\eta }^2\right)$ must be specified to ensure that the model is identifiable. The Level 2 priors on ${\tilde{\xi }}_{b,r}$ and ${\tilde{\eta }}_{b,r}$ facilitate information borrowing across cancer subtypes. Specifically, for each (dose, schedule) regime r, we assume that {${\tilde{\xi }}_{b,r}$, b = 1, ⋯, C} (or {${\tilde{\eta }}_{b,r}$, b = 1, ⋯, C}) are generated from a common normal distribution, where $\left({\ddot{\xi }}_r,{\ddot{\eta }}_r\right)$ are the mean (toxicity, efficacy) effects of regime r = (d, s), and $\left({\tau }_{\xi }^2,{\tau }_{\eta }^2\right)$ characterize the degree of heterogeneity of toxicity and efficacy, respectively, between subtypes. As ${\tau }_{\xi }^2,{\tau }_{\eta }^2\to 0$, model (2.1) shrinks to the homogeneous case for which the regime effects in different subtypes are the same. In the motivating MM trial, based on clinical experience the toxicity distribution is assumed to be homogeneous between subgroups, but efficacy may be heterogeneous between subgroups. We thus simplify the model by setting ${\tau }_{\xi }^2=0$, while ${\tau }_{\eta }^2\ne 0$. In general, however, the model can account for heterogeneous toxicity by specifying ${\tau }_{\xi }^2\ne 0$.

Since ${\tau }_{\eta }^2$ controls the degree to which efficacy information is borrowed across different tumor subtypes, rather than fixing ${\tau }_{\eta }^2$, we estimate its value adaptively based on the observed data. The choice of the prior on ${\tau }_{\eta }^2$ is critical to ensure good performance of the proposed design. To leverage information sharing, we follow the suggestion of Gelman (2006) by assuming a half-Cauchy(ψ₀, γ₀) prior on τ_η in Level 3 of the model, where ψ₀ is the location parameter and γ₀ is the scale parameter. When ψ₀ = 0 and γ₀ is large, this prior is weakly informative. To account for the common assumption that the risk of toxicity increases monotonically with dose for each schedule, in the Level 3 prior we impose an order constraint on {${\ddot{\xi }}_{d,s}$, d = 1, …, D} for each s at each Markov chain Monte Carlo sampling step. This ensures that the latent variable for toxicity increases stochastically in d. In contrast, we do not impose any monotonicity restriction on efficacy, so that the dose–efficacy curve is very flexible and can take a wide variety of shapes. In the MM trial, there is no ordering based on infusion schedule. If the infusion times would affect the risk of toxicity in other settings, however, such prior ordering information also can be similarly incorporated in our design.

Under the hierarchical model (2.1), given $\left({\tilde{\xi }}_{b_i,r_i},{\tilde{\eta }}_{b_i,r_i}\right)$, the joint distribution of (ξ_i, η_i) can be obtained by integrating out (u_i, v_i), which yields

$${\xi }_i,{\eta }_i\mid {\mathit{\mu }}_{b_i,r_i},{\Sigma }_{\xi ,\eta }\stackrel{\text{ind}}{~}\text{BN}\left({\mathit{\mu }}_{b_i,r_i},{\Sigma }_{\xi ,\eta }\right),i=1,\dots ,n.$$ (2.2)

The mean vector μ_bi,ri depends on both the i^th patient’s cancer subtype b_i and the treatment regime r_i = (d_i, s_i), with ${\mu }_{b_i,r_i}=\left({\tilde{\xi }}_{b_i,r_i},{\tilde{\eta }}_{b_i,r_i}\right)$, and

$${\Sigma }_{\xi ,\eta }={\Sigma }_{u,v}+\left[\begin{array}{cc}{\sigma }_{\xi }^2& 0\\ 0& {\sigma }_{\eta }^2\end{array}\right].$$

Suppose, temporarily, that the data of the first n patients are completely observed, and let $D_n^{\text{com}}=\left\{\left(x_i,y_i\right),i=1,\dots ,n\right\}$ denote the complete dataset and θ = {μ_b,r, b = 1, …, B, d = 1, …, D, s = 1, …, S} ∪ Σ_ξ,η. The complete data likelihood, based on $D_n^{\text{com}}$, is given by

$$L\left(\mathit{\theta }\mid D_n^{\text{com}}\right)=\prod _{i=1}^n{\int }_{{\ell }_{x_i}}^{{\ell }_{x_i+1}}{\int }_{{\ell }_{y_i}}^{{\ell }_{y_i+1}}f\left({\xi }_i,{\eta }_i\mid {\mu }_{b_i,r_i},{\Sigma }_{\xi ,\eta }\right)\text{d}{\eta }_i\text{d}{\xi }_i,$$

where $x_i,y_i=0,1,f\left({\xi }_i,{\eta }_i\mid {\mu }_{b_i,r_i},{\Sigma }_{\xi ,\eta }\right)$ is the distribution induced by (2.2), and the cutoff vector (ℓ₀, ℓ₁, ℓ₂) = (−∞, 0, ∞). Let π(θ | θ₀) be the joint prior distribution on θ based on the hierarchical model (2.1). The joint posterior of θ is given by $\pi \left(\theta |{\theta }_0,D_n^{\text{com}}\right)\propto \pi \left(\theta \mid {\theta }_0\right)L\left(\theta \mid D_n^{\text{com}}\right)$.

2.2. Imputation model

When the accrual of new patients is fast relative to the duration of the toxicity and efficacy assessment periods, T_X and T_Y, there will be some patients for whom X_i and Y_i are not known at the interim time when adaptive decisions must be made for newly enrolled patients. In the MM trial, the toxicity assessment window is [0, T_X] = [0, 30] days, while efficacy is defined as complete remission at the T_Y = 90 day evaluation. If, for example, the accrual rate is 6 patients per month, then an average of 18 new patients will be accrued while waiting to evaluate Y_i for the last enrolled patient. In other words, at the time of decision making, both the toxicity and efficacy data of previously treated patients are subject to temporary missingness, which is nonignorable (Liu et al., 2013). Once the patients who have pending Y_i values reach their 90-day assessment times, their (toxicity, efficacy) outcomes have been observed completely. If the accrual were suspended repeatedly until all previously treated patients were fully assessed, this would lead to an impractically lengthy trial, and would greatly delay the treatment of new patients, which cannot be done in an actual trial. To address this realistically, we exploit additional interim auxiliary information related to the unobserved (X_i, Y_i), as follows.

Let t_i ≤ max{T_X, T_Y} denote the follow-up time of patient i, within the observation windows, at some interim decision-making time. Let U_i denote the time to toxicity, with δ = (δ_X,i, δ_Y,i) the response indicator vector of whether each outcome of the i^th subject has been observed by t_i. The binary toxicity outcome X_i is observed if U_i ≤ t_i ≤ T_X, so X_i = 1, in which case δ_X,i = 1, or the patient has finished the assessment without experiencing toxicity, i.e., t_i ≥ T_X and U_i > T_X, so X_i = 0. In contrast, the efficacy outcome is observed if and only if the patient has reached their efficacy assessment time, that is, δ_Y,i = I(t_i ≥ T_Y). For example, if t_i < U_i then X_i is missing and δ_X,i = 0 at t_i. Therefore, the observed data for the first n patients are $D_n^{\text{obs}}=\left\{\left({\delta }_{X,i},{\delta }_{Y,i},t_i,{\tilde{X}}_i,{\tilde{Y}}_i\right),i=1,\dots ,n\right\}$, where ${\tilde{X}}_i={\delta }_{X,i}{X}_i$ and ${\tilde{Y}}_i={\delta }_{Y,i}{Y}_i$.

To exploit information on low grade toxicity that may be available before the binary toxicity outcome X_i is observed, we define a binary indicator, L_i, of whether the i^th patient has experienced low-grade toxicity (L_i = 1) or not (L_i = 0). We assume that a patient with low-grade toxicity is more likely to experience DLT, formally Pr(X_i = 1 | L_i = 1) > Pr(X_i = 1 | L_i = 0), so L_i may be used to help predict as yet unobserved X_i. In our example, L_i is available much sooner than T_X. We assume that, if a patient has finished the toxicity assessment without experiencing any DLT, then his/her time-to-toxicity outcome is censored at T_X. The observed event indicator is ${\tilde{X}}_i$, with ${\tilde{X}}_i=1$ if that patient i had toxicity, and ${\tilde{X}}_i=0$ if the time to toxicity for patient i is censored by the follow-up time t_i or maximum toxicity assessment time T_X. Formally, ${\tilde{X}}_i=\text{I}\left\{U_i\le \text{min}\left(t_i,T_X\right)\right\}$. We assume the following proportional hazards (PH) model for the distribution of the time to toxicity.

$$\begin{array}{rr}\hfill \text{PH model}:& \lambda \left(U_i\mid L_i\right)={\lambda }_0\left(U_i\right)\text{ exp}\left(\beta L_i\right),i=1,\dots ,n,\hfill \\ \hfill \text{Baseline model}:& U_i\mid L_i=0,p,q\stackrel{\text{i.i.d}}{~}\text{Weibull}\left(p,q\right),i=1,\dots ,n,\hfill \\ \hfill \text{Priors}:& \beta \mid {\sigma }_{\beta }~\text{N}\left(0,{\sigma }_{\beta }\right)\text{I}\left(0,\infty \right),\hfill \\ \hfill & p\left|{\alpha }_p,{\beta }_p~\text{Gamma}\left({\alpha }_p,{\beta }_p\right),q\right|{\alpha }_q,{\beta }_q~\text{Gamma}\left({\alpha }_q,{\beta }_q\right),\hfill \end{array}$$ (2.3)

where λ(U_i | L_i) is the conditional hazard function of the time to toxicity given the low-grade toxicity indicator L_i, λ₀(U_i) is the baseline hazard, and θ₁ = (σ_β, α_p, β_p, α_q, β_q) are hyperparameters. We assume that the baseline survival follows a Weibull distribution, which is flexible enough to characterize the time-to-toxicity data in our MM setting. Let f(U_i | L_i, p, q, β) be the density of U_i and denote the joint posterior distribution

$$\begin{gathered} \pi \left(p,q,\beta \mid D_n^{\text{obs}},{\theta }_1\right)\propto \pi \left(p,q,\beta \mid {\theta }_1\right)L_T\left(D_n^{\text{obs}}\mid p,q,\beta \right) \\ =\pi \left(p,q,\beta \mid {\theta }_1\right)\prod _{i=1}^{n}f{\left(t_i\mid L_i,p,q,\beta \right)}^{{\tilde{X}}_i}S{\left(\text{min}\left(t_i,T_X\right)\mid L_i,p,q,\beta \right)}^{\left(1-{\tilde{X}}_i\right)}, \end{gathered}$$

where S(· | L_i, p, q, β) is the survival function. After obtaining the posterior distribution $\pi \left(p,q,\beta \mid D_n^{\text{obs}},{\theta }_1\right)$, the missing toxicity outcome with δ_X,i = 0 can be imputed by a Bernoulli random variable with the probability of DLT given by

$$\begin{gathered} \text{Pr}\left(X_i=1\mid {\delta }_{X,i}=0,D_n^{\text{obs}},p,q,\beta \right)=\text{Pr}\left(U_i\le T_X\mid U_i\ge t_i,D_n^{\text{obs}},p,q,\beta \right) \\ =\frac{S\left(t_i\mid l_i,p,q,\beta \right)-S\left(T_X\mid l_i,p,q,\beta \right)}{S\left(t_i\mid l_i,p,q,\beta \right)}. \end{gathered}$$

In the MM trial, 90-day response is defined as complete response (CR) or partial response (PR). In therapy of MM, CR is defined as is negative immunofixation on analysis of blood serum and urine, disappearance of any soft tissue plasmacytomas, and < 5% plasma cells in the bone marrow, and PR is defined as ≥ 50% of blood serum M-protein and ≥ 90% reduction in urinary M-protein level within 24 hours. Additional details are given by Durie et al. (2006). Thus, early measurement of the M-protein in the serum and urine are associated with the 90-day response indicator Y_i.

Let Z_ik denote the biomarker measurement for the i^th patient at time $t_{ik}^{\prime }$, k = 1, …, K_i, where K_i is the total number of biomarker measurements of the i^th patient by the decision-making time t_i. We model the longitudinal biomarker measurements Z_ik and link them to the efficacy outcome Y_i using the following hierarchical model.

$$\begin{array}{ll}\hfill \text{Bioactivity Model}:& Z_{ik}\mid t_{ik}^{\prime },w_0,w_{b_i,r_i},{\sigma }_z^2\stackrel{\text{ind}}{~}\text{N}\left(w_0+w_{b_i,r_i}{t}_{ik}^{\prime },{\sigma }_z^2\right),\hfill \\ \hfill \text{Link Model}:& {\eta }_i\mid w_{b_i,r_i},\mathit{\alpha },{\sigma }_{\eta }^2\stackrel{\text{ind}}{~}\text{N}\left({\alpha }_0+{\alpha }_1{w}_{b_i,r_i}+{\alpha }_2{w}_{b_i,r_i}^2,{\sigma }_{\eta }^2\right),\hfill \\ \hfill \text{Level }1\text{ Priors}:& w_{b,r}\mid {\overline{w}}_r,{\tau }_w^2\stackrel{\text{i.i.d.}}{~}\text{N}\left({\overline{w}}_r,{\tau }_w^2\right),b=1,\dots ,B\hfill \\ \hfill & w_0\mid {\tau }_{w_0}^2~\text{N}\left(0,{\tau }_{w_0}^2\right),\hfill \\ \hfill & {\alpha }_1,{\alpha }_2\mid {\tau }_{\alpha }^2\stackrel{\text{i.i.d.}}{~}\text{N}\left(0,{\tau }_{\alpha }^2\right),\hfill \\ \hfill & {\sigma }_z^2~\text{IGamma}\left({\alpha }_z,{\beta }_z\right),\hfill \\ \hfill \text{Level 2 Priors}:& {\overline{w}}_r\mid {\overline{w}}_0,{\nu }_w^2\stackrel{\text{i.i.d.}}{~}\text{N}\left({\overline{w}}_0,{\nu }_w^2\right),\hfill \\ \hfill & {\tau }_w^2~\text{half-Cauchy }\left({\psi }_0,{\gamma }_0\right),\hfill \end{array}$$ (2.4)

where α = (α₀, α₁, α₂) and ${\theta }_2=\left({\sigma }_{\eta }^2,{\alpha }_0,{\tau }_{w_0}^2,{\tau }_{\alpha }^2,{\alpha }_z,{\beta }_z,{\overline{w}}_0,{\nu }_w^2,{\psi }_0,{\gamma }_0\right)$ are hyperparameters. In particular, α₀ must be fixed to make the model identifiable. In the bioactivity model, w₀ is the intercept, which can be viewed as the baseline biomarker value, and the second term $w_{b_i,r_i}{t}_{ik}^{\prime }$ captures the trajectory of the biomarker. The relationship between the latent variable η_i and the random effect $w_{b_i,r_i}$ induces association between the biomarker measurements and the efficacy outcome. The random effect w_b,r depends on the patient’s disease subtype and treatment regime. We also assume that {w_b,r, b = 1, …, B} are sampled from a common normal distribution with variance parameter ${\nu }_w^2$, which determines the amount of information shared across subtypes. In other words, ${\nu }_w^2$ is another heterogeneity parameter derived from the bioactivity data.

Denote w = {w_b,r} for b = 1, …, B and all DS pairs r = (d, s). We denote the posterior distribution of (α, w) under the Bayesian hierarchical model (2.4) by $\pi \left(\alpha ,w|{\theta }_2,{\tilde{D}}_n^{\text{obs}}\right)$, where ${\tilde{D}}_n^{\text{obs}}=D_n^{\text{obs}}\cup \left\{z_i,i=1,\dots ,n\right\}$ with z_i = {z_ik, k = 1, …, K_i}. A missing efficacy outcome, with δ_Y,i = 0, can be imputed as a Bernoulli random variable with success probability

$$\text{Pr}\left(Y_i=1\mid {\delta }_{Y,i}=0,{\tilde{D}}_n^{\text{obs}},\mathit{\alpha },w,{\sigma }_{\eta }^2\right)={\int }_{{\ell }_1}^{{\ell }_2}f\left({\eta }_i\mid {\tilde{D}}_n^{\text{obs}},\mathit{\alpha },w,{\sigma }_{\eta }^2\right)\text{d}{\eta }_i,$$

where the conditional distribution $f\left({\eta }_i\mid {\tilde{D}}_n^{\text{obs}},\alpha ,w,{\sigma }_{\eta }^2\right)$ is derived from (2.4).

To deal with temporarily missing toxicity/efficacy data, we adopt a Bayesian data augmentation (BDA) approach (Daniels and Hogan, 2008; Little and Rubin, 2014) to iteratively impute the missing data using the available auxiliary information (See Supplementary Material for detailed sampling steps). We sample from the posterior distribution of the model parameters based on the dataset completed using the imputed values. In the MM study, low-grade toxicity may be observed quickly, and some bioactivity variables are measured repeatedly. We use this auxiliary information to impute missing values of X_i and Y_i, so that adaptive treatment decisions can be made in real time based on the completed dataset. The BDA algorithm iterates between two steps: an imputation (I) step, and a posterior (P) step, in which posterior samples of the parameters are simulated based on the imputed data. Liu et al. (2013) and Jin et al. (2014) used a similar data augmentation approach in dose-finding studies with incompletely observed outcomes. However, they only used follow-up time and did not exploit auxiliary variables to help impute missing outcomes.

We carry out the BDA procedure for posterior sampling using JAGS via the R2jags package (Su and Yajima, 2015). The posterior samples obtained from JAGS can be utilized directly to calculate the posterior utility functions as specified in Section 3. In general, it takes approximately 2s in R to complete one BDA procedure with three chains and a total of 9,000 posterior samples. When the sample size is 180 and the posterior estimates are estimated for each subtype after a cohort of three patients have been treated, it requires about 6 minutes to simulate one trial. We thus used a high performance computing cluster to conduct runs in parallel across 200 computational nodes.

3. Trial design

3.1. Utility function

We take a utility-based approach to quantify efficacy-toxicity risk-benefit trade-offs. To do this, a numerical utility U(x, y) is elicited for each of the elementary outcome pairs (x, y) = (0, 0), (1, 0), (0, 1), or (1, 1). A consistent utility function must satisfy the admissibility constraints U(1, 0) < min{U(1, 1), U(0, 0)} and max{U(1, 1), U(0, 0)} < U(0, 1). It is convenient to fix the best case utility U(0, 1) = 100 and the worst case utility U(1, 0) = 0, although this is not necessary, and ask the clinicians to specify the utilities U(0, 0) and U(1, 1) between 0 and 100 for the two remaining intermediate outcome combinations. If U(1, 1) > U(0, 0), then efficacy is considered more important than toxicity, while if U(1, 1) < U(0, 0), then avoiding toxicity matters more than achieving efficacy. For illustrations of the choice of U(x, y), see Houede et al. (2010), Thall and Nguyen (2012), or Yuan, Nguyen and Thall (2016).

For each disease subtype b, the mean utility of regime r = (d, s) given θ is

$$\begin{gathered} u\left(\mathit{\theta },b,r\right)=\text{E}\left\{U\left(X,Y\right)\mid b=b,r=\left(d,s\right),\theta \right\}= \\ =\sum _{x=0}^1\sum _{y=0}^{1}U\left(x,y\right)\text{Pr}\left\{X=x,Y=y\mid b=b,r=\left(d,s\right),\theta \right\}. \end{gathered}$$

The posterior probability that the treatment regime r = (d, s) achieves the highest utility within schedule s is

$$\omega \left(b,r\right)=\text{Pr}\left[u\left(\mathit{\theta },b,r\right)=\underset{r^{\prime }\in \left\{\left(1,s\right),\dots ,\left(D,s\right)\right\}}{\text{max}}\left\{u\left(\theta ,b,r^{\prime }\right)\right\}|\mathbf{\Theta },{\tilde{D}}_n^{\text{obs}}\right],$$

where Θ = (θ₀, θ₁, θ₂). The probability of assignment to regime r = (d, s) under the proposed AR procedure, which is given in detail below, depends on ω(b, r). This is different from the AR procedures used by Thall and Nguyen (2012), Lee, et al. (2015), and others, where the AR probabilities are defined in terms of posterior mean utilities, i.e., $\tilde{\omega }\left(b,r\right)=\text{E}\left[u\left(\theta ,b,r\right)\mid \mathbf{\Theta },{\tilde{D}}_n^{\text{obs}}\right]$. While $\tilde{\omega }\left(b,r\right)$ summarizes only the first moment of the posterior of u(θ, b, r), the probability ω(b, r) is more variable because it accounts for the posterior distribution of u(θ, b, r). Hence, AR probabilities defined in terms of ω(b, r) lead to more extensive exploration of the set of regimes, so ω(b, r) has a smaller chance of getting stuck at suboptimal regimes.

3.2. Adaptive randomization

Let π_X(b, r) = Pr{X = 1 | b, r} be the marginal probability of toxicity and π_Y(b, r) = Pr{Y = 1 | b, r} the marginal probability of efficacy, for b = 1, …, B, d = 1, …, D, and s = 1, …, S, where r = (d, s). For each subtype b, we define a set of admissible regimes by adaptively screening out any regimes with either excessively high toxicity or unacceptably low efficacy based on the interim data. For each b, denote a fixed elicited upper limit ${\overline{\pi }}_X$ on ${\pi }_X^T\left(b,r\right)$ and a fixed elicited lower limit ${\underset{\_}{\pi }}_Y$ on ${\pi }_y^E\left(b,r\right)$. The set of admissible regimes ${\mathcal{A}}_b$ for disease subtype b consists of all r = (d, s) that satisfy the two requirements

$$\text{Pr}\left\{{\pi }_X\left(b,r\right)>{\overline{\pi }}_X\mid \mathbf{\Theta },{\tilde{D}}_n^{\text{obs}}\right\}<c_X\text{ and Pr}\left\{{\pi }_Y\left(b,r\right)<{\underset{\_}{\pi }}_Y\mid \mathbf{\Theta },{\tilde{D}}_n^{\text{obs}}\right\}<c_Y,$$

where c_X and c_Y are fixed cutoff probabilities calibrated to obtain a design with good operating characteristics. If no regimes satisfy these admissible criteria, the trial is stopped early and no regime is selected.

The primary objective of the MM basket trial is to find the optimal admissible treatment regime r = (d, s) for each cancer subtype b. Since toxicity assessment is much faster than efficacy assessment, we consider a two-stage trial design. In stage 1, patients in each subtype are randomized fairly among schedules. Since toxicity is observable much earlier than efficacy, the toxicity data play a major role in stage 1, with treatment regimes that have excessively high toxicity probabilities within a subgroup being ruled out. In stage 2, as previously missing efficacy outcomes are observed for patients who have completed their efficacy assessment, this efficacy data is included in the decision making. We adaptively randomize the remaining patients among all acceptable regimes across different schedules.

Assume that patients are recruited sequentially to each schedule within each disease subtype. Let N_max be the maximum total sample size, and p_b the prevalence of subtype b = 1, …, B, so ${\sum }_{b=1}^B{p}_b=1$. For each subtype b, we fairly allocate κp_bN_max patients to each schedule in stage 1. Thus, the remaining number of patients in stage 2 is (1 − κS)p_bN_max. The two-stage trial is conducted as follows.

Stage 1.

If the next patient has disease subtype b, determine the admissible set ${\mathcal{A}}_b$ based on the most recent data ${\tilde{D}}_n^{\text{obs}}$.

• 1.1 Randomly choose a schedule, s, with probability 1/S each.

• 1.2 If the selected schedule s has never been tested, then start the subtrial for this schedule at the lowest dose, i.e., r =(1, s). Otherwise, subject to the constraint that no untried dose may be skipped when escalating, randomly choose an admissible regime $r=\left(d,s\right)\in {\mathcal{A}}_b$, d = 1, …, D, for the next patient with AR probability proportional to ω(b, r).

• 1.3 The subtrial for subtype b is either stopped when the maximum sample size κp_bN_max is reached, or terminated early if no dose within this schedule is admissible for subtype b.

Stage 2.

For each newly enrolled patient in subtype b, first determine the optimal admissible regime $r_b^{*}\left(s\right)=\left(d_b^{*}\left(s\right),s\right)$ that has largest posterior probability of having the maximum mean utility within each s, i.e.,

$$d_b^{*}\left(s\right)=\underset{d\in \left\{1,\dots ,D\right\}}{\text{arg max}}\omega \left(b,r\right)\text{I}\left\{r\in {\mathcal{A}}_b\mid r=\left(d,s\right)\right\},s=1,\dots ,S.$$

Then choose the schedule s ∈ {1, ⋯, S} with probability proportional to

$$\omega \left(b,r_b^{*}\left(s\right)\right)=\text{Pr}\left[u_{\theta }\left(b,r_b^{*}\left(s\right)\right)=\underset{r_b^{\prime }\in \left\{r_b^{*}\left(1\right),\dots ,r_b^{*}\left(S\right)\right\}}{\text{max}}\left\{u_{\theta }\left(b,r_b^{\prime }\right)\right\}\mid \mathbf{\Theta },{\tilde{D}}_n^{\text{obs}}\right],$$

and assign the new patient to regime $\left(d_b^{*}\left(s\right),s\right)$. In other words, the second stage adaptively randomizes patients to the best dose–schedule regime within each schedule. Repeat this process until the remaining patients have been treated in the second stage. If no regime is admissible for subtype b, then stop the trial for that subtype.

At the end of the study, based on the complete data D_Nmax, for each subtype b = 1, …, B, the optimal treatment regime $r_b^{*}=\left(d_b^{*},s_b^{*}\right)$ is defined as that with the largest posterior probability of having the maximum mean utility among all the regimes, formally

$$r_b^{*}=\underset{r\in {\mathcal{A}}_b}{\text{arg max}}\text{ Pr}\left[u\left(\theta ,b,r\right)=\underset{r^{\prime }}{\text{max}}\left\{u_{\theta }\left(b,r^{\prime }\right)\right\}\mid \mathbf{\Theta },{\tilde{D}}_n^{\text{obs}}\right].$$

3.3. Design parameter calibration

To obtain a design with good performance, one must carefully calibrate the numerical values of both the hyperparameters, Θ = (θ₀, θ₁, θ₂), and the design parameters, (N_max, κ, ${\overline{\pi }}_X$, ${\underset{\_}{\pi }}_Y$, c_X, x_Y). In general, this can be done as follows. The method requires prior values of π_X(b, r) and π_Y (b, r) to be elicited from the physicians who are planning the trial, for each subgroup b and regime r.

The method uses the idea of prior expected sample size (ESS) given by Morita et al. (2008) to specify the hyperparameters θ₀, θ₁, θ₂. As the first step of an iterative process, fix the initial values of (${\sigma }_{\xi }^2$, ${\sigma }_{\eta }^2$, Σ_u,v) and (${\nu }_{\xi }^2$, ${\nu }_{\eta }^2$, ψ₀, γ₀). Given a regime r, the values of ξ₀ and η₀ can be obtained by matching the mode of the prior of each π_X(b, r) and π_Y (b, r) with the corresponding elicited value. Using the initial fixed hyperparameters, prior samples of π_X(b, r) and π_Y (b, r) values are generated using the hierarchical model (2.1). Following the approach of Lee, et al. (2015), each prior sample is fit to a Beta(a, b) distribution using the method of moments, with the prior ESS approximated as a + b. The hyperparameter θ₀ can be calibrated repeatedly until a + b is near 1 for each (b, r) combination, which gives a reasonably vague prior. A similar procedure can be used to obtain θ₁ and θ₂. Additional details, including guidelines for choosing the numerical prior and design parameter values, are given in Section S2 of Supplementary Material.

The upper limit ${\overline{\pi }}_X$ on π_X(b, r), and the lower limit ${\underset{\_}{\pi }}_Y$ on π_Y (b, r) also must be specified by the clinician. In practice, the maximum sample size N_max of a phase I-II trial is specified based on practical limitations, and choosing N_max may be informed by preliminary trial simulations to assess the design’s performance for a range of different feasible values. We recommend that at least D patients are assigned to each schedule in stage 1 for each subtype, to ensure that each dose within each schedule has a reasonable probability of being tried, unless the lowest dose is found to be unsafe for that schedule. Formally, this implies that κ ≥ max_{b∈{1,…,B}}{D/(p_bN^max)}. For example, given N_max = 180, D = 3, C = 3, and (p₁, p₂, p₃) = (3/12, 4/12, 5/12), κ should be greater than 1/15, to ensure that at least one patient in subtype 1 can be assigned to each dose for each schedule in stage 1. When N_max is adequate, we recommend allocating more patients to stage 1, to ensure that the preliminary estimate of the subgroup-specific optimal treatment regime for each subtype is reasonably accurate. In the MM study, N_max = 180, and we assign at least 3D = 9 patients to each schedule for each subtype in stage 1.

4. Simulation Study

4.1. Simulation design

A simulation study to assess the proposed design’s performance was designed to be similar to the MM trial, with B = 3 different subtypes and patients in each subtype assigned to one of the nine dose–schedule regimes, for a total of 27 subtype-specific dose–schedule regimes. The toxicity window was T_X = 30 days with the same upper limit ${\overline{\pi }}_X=.15$ for all ${\pi }_X^T\left(b,r\right)$. Low-grade toxicity was defined as grade 1 or 2 toxicity observed immediately. Bioactivity was simulated as a longitudinal variable measured on each of days 10, 20, ⋯, 90. Assuming equal subgroup proportions (p₁, p₂, p₃) = (1/3, 1/3, 1/3), the maximum sample size N_max = 180 leads to an average of 6.6 patients assigned to each of the 27 subgroup-regime combinations. We also performed a sensitivity analysis to investigate the design’s performance for other (p₁, p₂, p₃) vectors. We set κ = 0.15 so that the stage 1’s sample size was 81. We assumed an accrual rate of 10 patients per month, with patients arriving according to a Poisson process, so it took approximately 18 months to accrue 180 patients. The proposed design was examined under 12 different scenarios. The assumed fixed marginal probabilities (π_X(b, r), π_Y (b, r)) in each scenario are given in Table S1 of the Supplementary Material, and the true mean utilities E(U(X, Y) | b, r) are given in Table S2 of the Supplementary Material. The 12 scenarios have six homogeneous cases and six corresponding heterogeneous cases. For each homogeneous case, say scenario i, π_Y (b, r) was the same across subtypes b = 1, 2, 3 for all r. For the corresponding heterogeneous case, {π_X(b, r) : b = 1, 2, 3} and π_Y (1, r) were the same as in scenario i, but π_Y (b, r)’s were different for b = 2, 3. Comparing the design’s performance under scenarios i and i + 1 thus shows what is gained by borrowing information across subtypes. Let $u_b^{\text{max}}$ denote the largest expected utility for all 9 regimes in subtype b. The set of subgroup-specific optimal treatment regimes (OTRs) are defined as those have expected utilities no less than $u_b^{\text{max}}-5$, so in particular more than one r may be nominally “optimal.” The OTRs for each subtype under each scenario are indicated in boldface in Table S2 of the Supplementary Material. The data-generating algorithms for the toxicity and efficacy outcomes (x_i, y_i), i = 1, …, n, and for the bioactivity and low-grade toxicity data, are provided in the Supplementary Material.

In the simulations, we denote the proposed basket phase I-II trial design as BTD₁₂. The detailed configuration of the BTD₁₂ is provided in Supplementary Material. For comparison, we simulated a simpler naive design that is used quite often in practice. This naive design collapses the different disease subtypes into a single population, based on the assumption of homogeneity. To deal with delayed outcomes, this design would make adaptive treatment assignment decisions for new patients only after the outcomes of the previously treated patients are all observed. To evaluate the advantage of borrowing information across subtypes by the BTD₁₂ design, as a comparator we also simulated a design that conducts separate, independent trials for each of the three subtypes, with maximum sample size p_bN_max for each subtype b = 1, …, B. This design, hereafter referred to as ITD₁₂, does not borrow information across subtypes for decision making. To evaluate the gain for borrowing information from additional bioactivity and low-grade toxicity data, we simulated the observed-data version of the BTD₁₂ (denoted by ${\text{BTD}}_{12}^{\text{O}}$). This design does not borrow any information from additional bioactivity or low-grade toxicity data. In addition, it makes treatment decisions based on the patients whose outcomes have been completely observed by the decision-making time. As a benchmark for comparison, we also simulated the complete-data version of the BTD₁₂ (denoted by ${\text{BTD}}_{12}^{\text{C}}$), which repeatedly suspends the accrual of new patients prior to each treatment assignment, to wait until all pending outcomes of perviously treated patients have been observed completely. As a result, ${\text{BTD}}_{12}^{\text{C}}$ has no missing outcomes. However, ${\text{BTD}}_{12}^{\text{C}}$ requires a very lengthy trial duration and is not feasible in practice. Nonetheless, it provides an upper bound for evaluating the performance of the proposed design since ${\text{BTD}}_{12}^{\text{C}}$ uses all the data in decision making. Lastly, we include the design proposed in Lin et al. (2019) for ordered cancer subtypes (hereafter referred to as OTD) in the simulation study. The OTD design requires strong prior information on the efficacy probability ordering among different subtypes. To adapt this design in our simulation setting, we assume that the treatment efficacy probabilities follow the ordering: subtype 3 > subtype 2 > subtype 1. For each design, the posterior distributions were updated after each cohort of three patients was treated. We simulated each design 1000 times under each scenario.

4.2. Simulation results

The simulation results of the proposed BTD₁₂ design are summarized in Tables S3 and S4 of the Supplementary Material, including within-subtype selection percentages and number of patients allocated to each regime. The simulation results show that BTD₁₂ has particularly high probabilities of selecting the optimal subgroup-specific treatment regimes, and it allocates most patients to the appropriate regimes. As mentioned, the marginal toxicity and efficacy probabilities are the same for subtype 1 in scenarios i and I + 1, for i an odd number, with the key difference that scenario i is a homogeneous case and scenario I + 1 is a heterogeneous case. Comparing the OTR selection percentages for subgroup 1 for each scenario pair i and I + 1 shows that the BTD₁₂ design generally has a greater probability of OTR identification, primarily because it borrows information across subtypes in the homogeneous cases.

We next focus on comparisons among the BTD₁₂, naive, ITD₁₂, OTD, and ${\text{BTD}}_{12}^{\text{C}}$ designs. Table 1 shows the percentages of selecting OTRs for each design. Table 2 provides other operating characteristics, including the percentage of patients allocated to overly toxic regimes with ${\pi }_X\left(b,r\right)>{\overline{\pi }}_X$, the percentage of patients allocated to inefficacious regimes with ${\pi }_Y\left(b,r\right)<{\underset{\_}{\pi }}_Y$, the percentage of trials selecting overly toxic regimes, summed across subgroups (so the maximum value is 300%), the average trial duration, and the trial efficiency index, defined as $\text{EI}={\sum }_{b=1}^B{p}_b\frac{{\widehat{u}}_b-{\overline{u}}_b}{u_b^{\text{max}}-{\overline{u}}_b}$, where ${\widehat{u}}_b$ is the empirical expected utility induced by one design for cancer subtype b, $u_b^{\text{max}}$ is the maximum utility among the regimes for subtype b, and ${\overline{u}}_b$ is the empirical mean utility induced by uniformly allocating patients to each of the dose–schedule regimes within subtype b. EI has a maximum value of 1, and measures how efficient the design is in treating the patients enrolled in the trial: If a design allocates as many patients as possible to the best treatment regime with $\text{E}\left(U\left(X,Y\right)\mid b,r\right)=u_b^{\text{max}}$, then its EI would approach one. Thus, larger EI corresponds to better design performance. Alternatively, if EI < 0, then the design is unacceptable since it performs worse than the equal allocation scheme.

Table 1:

Percentages of selecting optimal treatment regimes within each cancer subtype, for each of the five designs under each of the 12 scenarios in Table S1 of the Supplementary Material. Efficacy is assessed at day 90, and the assessment period for toxicity is 30 days. The accrual rate is 10 patients per month. Scenarios given in boxes correspond to heterogeneous cases. The subgroup-specific optimal treatment regimes are defined as those have expected utilities no less than $u_b^{\text{max}}-5$, where $u_b^{\text{max}}$ denotes the largest expected utility for all 9 regimes in subtype b.

Method	Scenarios												Average
	1	$\boxed{2}$	3	$\boxed{4}$	5	$\boxed{6}$	7	$\boxed{8}$	9	$\boxed{10}$	11	$\boxed{12}$
Cancer subtype 1
BTD12	91.7	80.1	80.4	70.2	73.4	47.8	85.7	72.3	75.9	69.1	85.1	84.8	76.4
Naive	96.6	43.2	85.6	49.8	69.3	19.5	92.8	46.5	83.5	64.2	93.2	91.0	69.6
ITD12	73.4	73.2	62.5	65.0	39.2	37.5	61.1	67.5	53.4	56.8	67.8	68.6	60.5
OTD	93.6	64.0	78.5	60.7	74.5	33.6	87.0	59.5	77.4	67.2	89.2	91.3	73.0
${\text{BTD}}_{12}^{\text{O}}$	91.6	74.3	81.2	68.0	68.8	45.8	85.8	68.4	72.5	69.1	85.4	85.4	74.7
${\text{BTD}}_{12}^{\text{C}}$	92.9	79.4	81.9	73.5	70.3	46.8	86.9	64.5	78.6	69.9	87.0	87.1	76.6
Cancer subtype 2
BTD12	93.6	76.8	79.4	70.5	73.9	61.3	84.9	81.6	74.2	79.3	87.6	86.6	79.1
Naive	96.6	18.9	85.6	18.6	69.3	26.3	92.8	47.1	83.5	48.2	93.2	91.0	64.3
ITD12	76.0	77.0	62.6	70.5	37.5	58.9	61.4	93.1	56.1	67.6	67.2	74.2	66.8
OTD	95.1	37.5	78.8	35.2	77.1	45.0	88.7	89.4	77.9	54.0	91.0	91.7	71.8
${\text{BTD}}_{12}^{\text{O}}$	91.3	72.8	80.2	66.1	70.6	62.2	84.0	81.0	74.8	74.4	86.2	88.1	77.7
${\text{BTD}}_{12}^{\text{C}}$	93.9	73.2	81.6	73.6	70.0	59.6	85.9	91.6	80.5	79.1	87.4	87.3	80.3
Cancer subtype 3
BTD12	92.8	77.0	79.6	84.4	73.6	73.2	84.0	53.2	76.3	51.2	85.3	83.9	76.2
Naive	96.6	3.6	85.6	66.4	69.3	32.5	92.8	19.3	83.5	41.0	93.2	91.0	67.4
ITD12	73.9	74.5	64.7	70.9	35.5	65.5	62.9	52.1	53.4	37.9	67.6	66.5	60.5
OTD	91.6	55.6	77.4	65.5	74.1	52.4	85.5	33.4	72.8	37.0	86.5	88.6	68.4
${\text{BTD}}_{12}^{\text{O}}$	94.2	77.4	80.8	77.2	70.0	68.7	84.1	49.1	74.3	52.4	86.2	85.0	75.0
${\text{BTD}}_{12}^{\text{C}}$	93.6	81.0	82.0	84.7	70.8	69.7	87.2	52.1	80.5	55.9	87.0	85.5	77.5

Table 2:

Operating characteristics based on five designs under the 12 scenarios in Table S1 of the Supplementary Material, assuming accrual rate of 10 patients per month. Scenarios given in boxes correspond to heterogeneous cases. “% selection of overly toxic regimes” is the sum of the percentages of selecting overly toxic regimes for all three subtypes, so the maximum value is 300%.

Method	Scenarios												Average
	1	$\boxed{2}$	3	$\boxed{4}$	5	$\boxed{6}$	7	$\boxed{8}$	9	$\boxed{10}$	11	$\boxed{12}$
% selection of overly toxic regimes
BTD12	1.4	1.4	1.1	7.3	4.3	2.6	13.3	41.1	49.7	53.5	12.2	18.0	17.2
Naive	0.0	0.9	0.0	3.3	3.3	0.3	6.0	27.9	32.4	32.4	6.0	11.7	10.4
ITD12	14.8	15.3	10.4	19.4	16.7	11.0	40.2	45.8	115.1	110.7	33.3	36.4	39.1
OTD	0.9	3.2	1.7	8.9	4.3	2.1	12.8	39.6	52.7	55.0	10.1	13.5	17.1
${\text{BTD}}_{12}^{\text{O}}$	1.0	2.8	0.6	10.0	4.0	2.4	16.8	42.8	53.6	55.2	16.1	20.4	18.8
${\text{BTD}}_{12}^{\text{C}}$	0.4	1.4	1.9	5.2	3.6	2.2	12.6	39.9	39.6	50.5	11.8	15.9	15.4
# patients allocated to overly toxic regimes
BTD12	16.2	16.0	15.7	22.0	9.5	6.5	22.1	30.2	81.2	79.7	17.5	18.9	28.0
Naive	12.2	12.4	12.2	18.2	6.8	4.1	17.8	25.4	74.0	74.9	12.4	14.0	23.8
ITD12	27.7	27.4	28.6	32.2	7.6	6.5	18.2	22.0	93.1	93.4	16.0	16.9	32.6
OTD	12.3	12.2	12.7	16.2	5.9	4.7	14.7	17.2	51.6	51.1	10.9	11.3	18.4
${\text{BTD}}_{12}^{\text{O}}$	20.4	19.4	19.6	26.9	10.1	7.6	24.5	31.4	84.6	84.5	19.8	19.8	30.7
${\text{BTD}}_{12}^{\text{C}}$	14.8	14.2	13.3	19.8	8.3	5.6	20.2	27.5	74.5	76.0	15.1	15.1	25.4
# patients allocated to subtherapeutic regimes
BTD12	9.9	12.1	37.8	43.6	9.2	10.6	47.5	53.5	21.4	27.7	64.6	70.2	34.0
Naive	9.0	17.1	32.9	59.2	7.9	9.0	41.2	72.0	19.8	33.1	58.3	62.8	35.3
ITD12	22.0	19.1	61.0	48.8	21.8	21.4	72.4	66.1	26.6	27.2	83.2	94.9	45.2
OTD	5.2	8.1	21.7	27.7	4.5	5.2	28.7	35.8	9.2	16.1	38.3	42.7	20.3
${\text{BTD}}_{12}^{\text{O}}$	10.9	12.1	39.4	42.2	9.7	10.3	50.4	54.6	19.3	26.2	64.3	71.8	34.3
${\text{BTD}}_{12}^{\text{C}}$	9.0	11.3	33.8	43.0	7.7	9.4	45.2	53.5	20.7	26.8	62.5	66.6	32.4
Trial efficiency index
BTD12	53.0	46.5	53.2	43.2	27.0	26.7	35.5	19.1	36.4	37.1	37.3	36.2	37.6
Naive	56.9	38.2	57.9	36.8	27.5	19.6	42.5	5.1	40.9	36.2	45.3	42.3	37.4
ITD12	28.0	27.0	35.4	33.6	26.8	14.9	19.6	17.1	24.6	27.2	25.8	23.2	25.3
OTD	41.9	33.2	44.6	29.2	18.6	16.8	28.7	6.4	29.5	27.3	38.3	30.6	21.0
${\text{BTD}}_{12}^{\text{O}}$	46.0	40.4	49.0	38.2	21.3	23.1	31.3	17.2	33.6	32.8	35.4	34.8	33.6
${\text{BTD}}_{12}^{\text{C}}$	54.0	48.6	56.6	45.7	26.8	26.9	38.7	22.1	40.0	39.9	40.5	39.8	40.0
Average trial duration (in months)
BTD12	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0
Naive	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0
ITD12	27.0	27.0	27.0	27.0	27.0	27.0	27.0	27.0	27.0	27.0	27.0	27.0	27.0
OTD	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0	21.0
${\text{BTD}}_{12}^{\text{O}}$	24.0	24.0	24.0	24.0	24.0	24.0	24.0	24.0	24.0	24.0	24.0	24.0	24.0
${\text{BTD}}_{12}^{\text{C}}$	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0	180.0

Table 1 shows that, in the homogeneous scenarios indexed by odd numbers, on average the naive design achieves the best performance. This is because the homogeneity assumption of the naive design is correct in these scenarios. The naive design thus can be treated as the oracle design in the homogeneous scenarios. However, in the heterogeneous scenarios where the model is misspecified, the naive design has the smallest OTR selection percentage, on average. Across the 12 scenarios, the within-subtype OTR selection percentage by BTD₁₂ is 76%, on average, which exceeds that provided by ITD₁₂ by approximately 15%. The advantage of BTD₁₂ over ITD₁₂ is quite large in the homogeneous scenarios, because BTD₁₂ borrows information across subtypes while ITD₁₂ does not. For example, in scenarios 1, 7, and 9, BTD₁₂ has more than a 20% greater chance of identifying the OTRs than ITD₁₂. The most striking case is scenario 5, in which the correct OTR selection percentage of BTD₁₂ is almost double that of ITD₁₂.

In the heterogeneous scenarios, indexed by even numbers, one concern is that excessive borrowing of information between subgroups may harm the performance of BTD₁₂. The simulations show that BTD₁₂ still outperforms ITD₁₂ in most of the heterogeneous scenarios, which may be attributed to the ability of BTD₁₂ to adaptively determine the amount of information borrowed from each subtype. For example, in scenario 4, subtype 2 has two OTRs, regimes (1, 1) and (2, 3), that are totally different for subtypes 1 and 3. The simulation results from Table 1, and Tables S3 and S4 in the Supplementary Material, together, show that BTD₁₂ is able to correctly detect this heterogeneity and allocate most patients to subtype-specific OTRs. The OTR selection percentage for subtype 2 is 70.5, which is particularly close to that based on ITD₁₂. In addition, since subtypes 1 and 3 have a common OTR, as a result, BTD₁₂ performs better than ITD₁₂ in terms of the OTR selection percentages for subtypes 1 and 3, due to adaptive information borrowing. There is only one OTR for each subtype, and the three subtype-specific OTRs are different in scenario 6, which is difficult for BTD₁₂ as information borrowing across subtypes may lead to incorrect OTR selections. However, the simulations show that, in scenario 6, BTD₁₂ still is superior to ITD₁₂. Another interesting result is seen in scenario 12, where the treatment effects are heterogeneous but the locations of the OTRs are the same across the three subtypes. In this case, it appears that BTD₁₂ benefits greatly from information borrowing, since it yields higher OTR selection percentages than ITD₁₂. Moreover, since the toxicity outcomes are assumed to be homogeneous across subtypes, there are always safety advantages from information sharing by BTD₁₂. Borrowing toxicity information across subtypes improves the reliability of the rules for screening out overly toxic regimes, whereas the ITD₁₂, which does not borrow information, has worse safety. This is shown by Table 2, which indicates that BTD₁₂ selects fewer overly toxic regimes and allocates fewer patients to overly toxic regimes, compared to ITD₁₂. Table 2 also shows that BTD₁₂ uniformly dominates the ITD₁₂ design in terms of trial efficiency and average trial duration.

Comparing the operating characteristics of the BTD₁₂ design and the observed-data ${\text{BTD}}_{12}^{\text{O}}$ design shows that borrowing information from bioactivity and low-grade toxicity data makes the BTD₁₂ more efficient. Table 2 shows that the EI values of BTD₁₂ are generally larger than those of ${\text{BTD}}_{12}^{\text{O}}$, and BTD₁₂ allocates fewer patients to overly toxic treatment regimes. In addition, BTD₁₂ yields higher selection percentages of optimal treatment regimes than ${\text{BTD}}_{12}^{\text{O}}$, especially in the heterogeneous scenarios 2, 4, 6, and 8. Recall that the complete data design ${\text{BTD}}_{12}^{\text{C}}$ is a benchmark that could never be used in practice since, by repeatedly suspending accrual, it would require an impossibly long trial duration. For example, ${\text{BTD}}_{12}^{\text{C}}$ would require up to 180 months (15 years) to complete a trial of 180 patients. Since the decisions of BTD₁₂ are made based on less data, unavoidably, it is less efficient than the optimal complete-data ${\text{BTD}}_{12}^{\text{C}}$ design, according to the EI values in Table 2. In terms of other metrics, such as OTR selection or overdose control, BTD₁₂ and ${\text{BTD}}_{12}^{\text{C}}$ have very similar performance, however. Although outcomes are missing early in the trial, it appears that BTD₁₂ is able to recover from the efficiency loss in the late-stage of the trial when more outcomes that had been temporarily missing are observed.

Comparing the BTD₁₂ basket design and the order-based OTD design, we found that these two methods yield similar OTR selection percentages in homogenous scenarios (indexed by odd numbers), where the ordering restriction of OTD was not violated. However, in heterogenous scenarios (indexed by even numbers) where the true subtype–efficacy structure does not satisfy the strong ordering restriction on the treatment efficacy probabilities among the three cancer subtypes, the performance of OTD is uniformly inferior to that of BTD₁₂. An interesting finding is that OTD generally yields smaller numbers of patients at overly toxic or subtherapeutic regimes than BTD₁₂, as noted in Table 2. This is potentially due to the fact that OTD puts highly informative priors on the efficacy probabilities, causing extensive information borrowing across different cancer subtypes. As a consequence, the convergence of parameter estimates based on OTD is faster, and thus OTD can quickly identify overly toxic or subtherapeutic regimes. But the accompanying risk with such a faster convergence rate is the higher chance of being trapped in suboptimal treatment regimes. On the other hand, BTD₁₂ does not assume a strong association among cancer subtypes, and uses observed data to adaptively determine the level of information sharing. At the beginning of the trial when the information contained in the observed data is sparse, BTD₁₂ tends to be more exploratory and test more untried regimes. Therefore, it has a higher number of patients treated at overly toxic of subtherapeutic regimes than BTD₁₂. Nevertheless, BTD₁₂ is much safer than the independent ITD₁₂ design. Furthermore, BTD₁₂ uses more information, leading to a higher EI than OTD across all scenarios. This in turn implies that more patients are treated at optimal or nearly optimal regimens based on BTD₁₂.

4.3. Sensitivity analyses

We carried out sensitivity analyses to assess the robustness of the BTD₁₂ design, by considering different (a) prevalence proportions for the three subgroups, (b) sample sizes for stage 1 while keeping N_max = 180 constant, (c) patient accrual rates, and (d) prior distributions on the heterogeneity parameters. In each sensitivity analysis, the other simulation configurations were unchanged from those in Section 4.1. In this section, we only describe the results (see Figure 1) under scenarios 1–4 of Table S1 in the Supplementary Material, since the substantive conclusions based on the other scenarios are the same.

Figure 1:

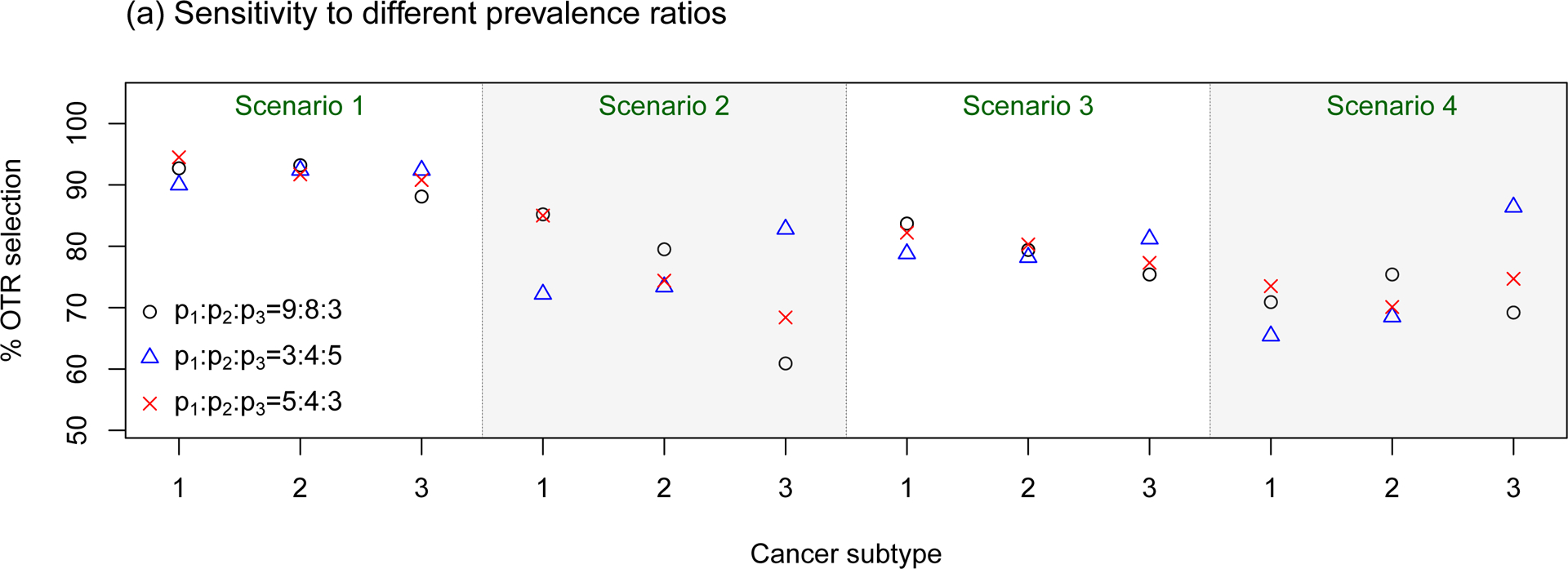
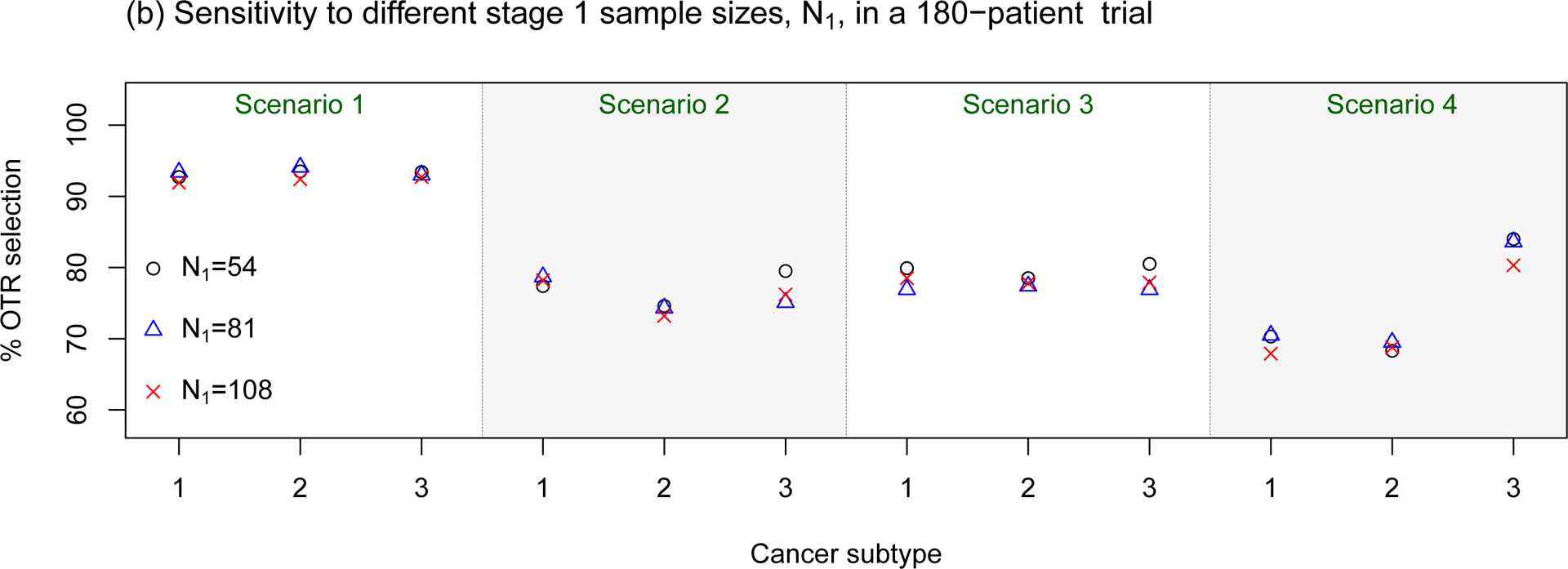
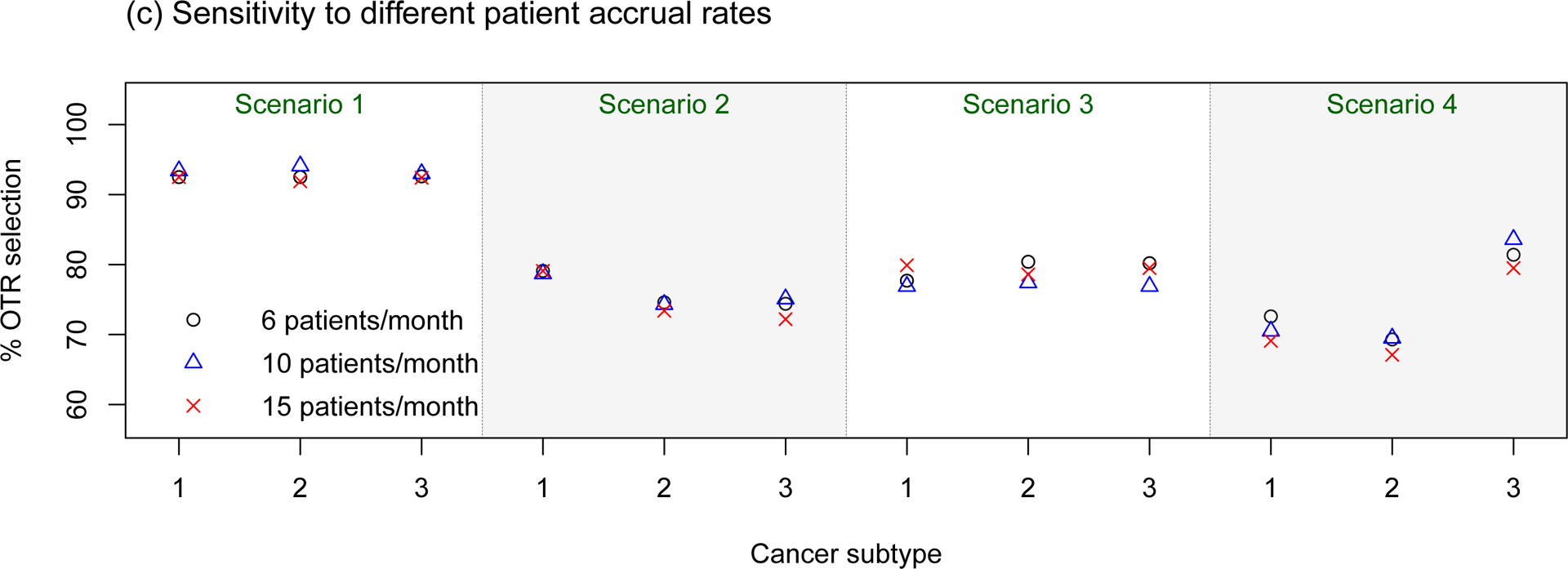
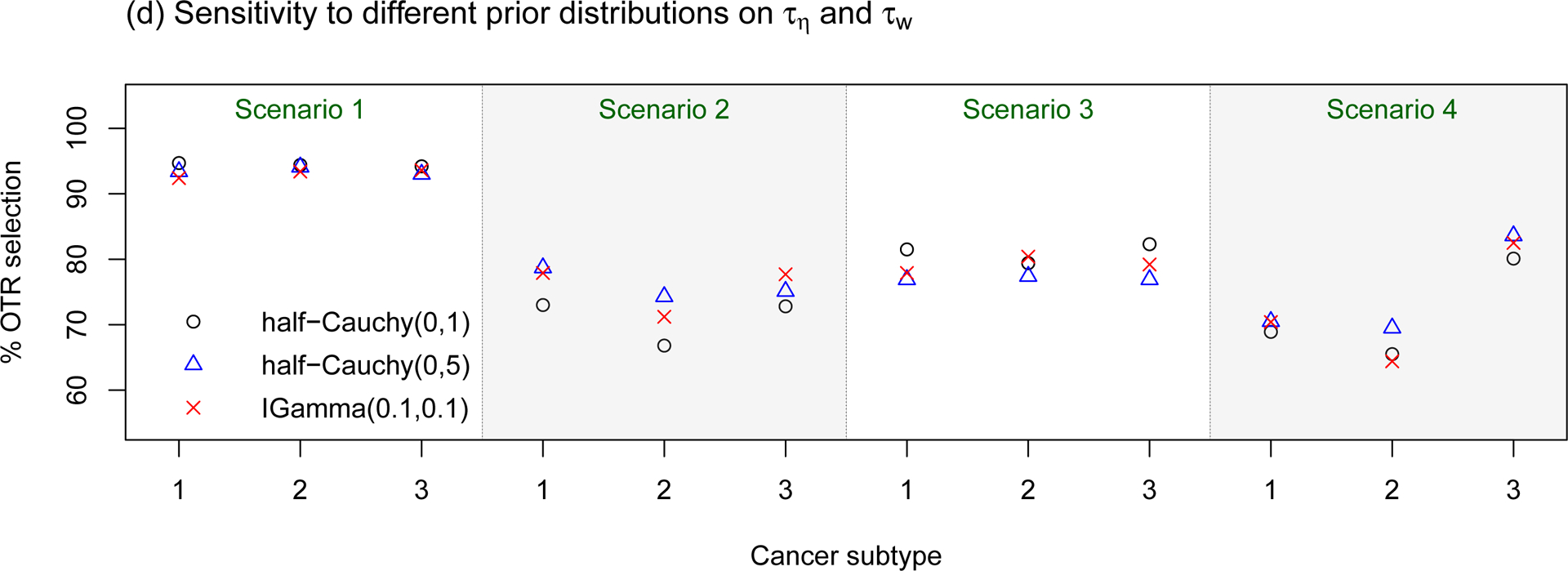
Sensitivity assessments of the proposed BTD₁₂ method to (a) different prevalence ratios (p₁ : p₂ : p₃); (b) different stage 1 sample sizes; (c) different patient accrual rates; (d) different prior distributions on τ_η and τ_w. The sensitivity assessments are conducted based on scenarios 1–4 of Table S1 in the Supplementary Material.

In sensitivity assessment (a), we considered three prevalence ratios. The first two were p₁ : p₂ : p₃ = 3 : 4 : 5, which enrolls more patients with subtype 3, and p₁ : p₂ : p₃ = 5 : 4 : 3, which enrolls more patients with subtype 1. Additionally, since in Table 5 of Fonseca, et al. (2009) MM patients are classified as {hyperdiploid, non-hyperdiploid, other} with respective percentages 45, 40, 15, we examined the design’s behavior using the corresponding values p₁ : p₂ : p₃ = 9 : 8 : 3. The simulation results show that, when the treatment effects are homogeneous (scenarios 1 and 3), the OTR selection percentages for the proposed design are not sensitive to the different prevalence ratios. However, when there are heterogeneous treatment effects, as in scenarios 2 and 4, the subtype-specific OTR selection percentage increases with the sample size of the subtype. For the most extreme imbalance p₁ : p₂ : p₃ = 9 : 8 : 3, lower OTR selection percentages of about 60% are seen in Scenario 2 and 70% in Scenario 4, which are slightly below the values for the case p₁ : p₂ : p₃ = 5 : 4 : 3, although the decrements are very small in Scenarios 1 and 3.

In sensitivity assessment (b), we evaluated the design under three different stage 1 sample sizes, N₁ = 54, 81, and 108, corresponding to κ = 0.10, 0.15, or 0.20, since N₁ = κN_maxB. The simulations suggest that the OTR selection percentage is not sensitive to these rather large differences in stage 1 sample size. However, we also found that smaller κ results in a larger EI (results not shown). This is because, when κ is small, more patients are enrolled in stage 2, which is the optimization stage. As a result, a design with a smaller value of κ generally allocates more patients to OTRs, and hence is more efficient in this regard.

In sensitivity assessment (c), we examined accrual rates of 6, 10, and 15 patients per month, which lead to respective average trial durations of 33, 21, and 15 months. Given the fixed toxicity/efficacy assessment windows, the accrual rate determines the amount of missing data at the time of decision making. The faster new patients arrive, the more likely it will be that patients treated previously will have missing outcomes that must be imputed. The simulation results displayed in panel (c) of Figure 1 show that the OTR selection percentage for the proposed method is quite robust to this range of accrual rates. However, the faster the accrual rate, the larger the amount of missing data in the decision-making process. Although the accrual rate does not affect the OTR selection percentage for BTD₁₂, additional simulations (results not provided) show that a fast accrual rate would make the proposed method less efficient and more aggressive.

In sensitivity assessment (d), we evaluated the effects of different prior distributions on the heterogeneity parameters τ_η and τ_w, which play critical roles in determining the amount of information borrowing between subtypes. We considered three cases: τ_η, ${\tau }_w\stackrel{\text{i.i.d.}}{~}\text{half-Cauchy}\left(0,1\right)$, τ_η, ${\tau }_w\stackrel{\text{i.i.d.}}{~}\text{half-Cauchy}\left(0,5\right)$, and τ_η, ${\tau }_w\stackrel{\text{i.i.d.}}{~}\text{IG}\left(0.1,0.1\right)$. The half-Cauchy(0, 1) prior places more probability mass on the homogeneous case, i.e., τ_η = τ_w = 0. The simulation results based on these three prior specifications are particularly close, suggesting that our design is not sensitive to these prior distributions.

5. Concluding remarks

The proposed phase I-II basket trial design finds the optimal subtype-specific dose–schedule by first assuming a three-level hierarchical model. Complications due to late-onset toxicity or efficacy outcomes are addressed by using a two-stage design with adaptive randomization, which is a natural approach to this problem. In stage 1, when most of the efficacy data are unavailable, toxicity data can be utilized for decision making to screen out unsafe treatment regimes. When more patients have completed their follow-up in stage 2, the efficacy outcome plays a major role in treating the remaining patients, and for choosing optimal (dose, schedule) regimes. To deal with different cancer subtypes, the Bayesian hierarchical model assumes that the dose–schedule treatment effects for different subtypes vary around a common mean, and thus facilitates adaptive shrinkage based on the observed data. The simulations show that the proposed design uniformly outperforms an approach that conducts separate independent trials within subgroups when the regime effects are homogeneous across subtypes. In addition, the operating characteristics of the proposed design are very close to those of the benchmark complete-data design, indicating that the efficiency loss due to missing data is minimal.

Although the assumed imputation models for missing values of X_i and Y_i may be incorrect, this will have negligible effects on the design’s performance, for several reasons. First, the imputation model only provides partial/indirect information, and the treatment-assignment decisions of the proposed method are mainly determined by the inference model. Second, outcomes are only temporarily missing. Once patients with pending outcomes have finished their entire assessments, temporarily unobserved outcomes become available and contribute to the estimation of the primary inference model (2.1). Third, the primary objective of the trial is not to obtain accurate inference on the subtype-specific regime-response relationships, but rather to identify optimal subtype-specific treatment regimes. Our simulations show that, even with misspecified imputation models, the proposed design still does a good job of allocating patients to optimal regimes and provides high probabilities of making correct selections.

While the Bayesian hierarchical model adaptively borrows information across cancer subtypes, a caveat is that it tends to shrink the subtype-specific treatment effects toward the common mean, which may lead to incorrect treatment assignment decisions when there is a mixture of homogeneous and heterogeneous subgroups. As suggested by an associate editor, we have considered four scenarios where the treatment effects are very similar for some subtypes and very different for the other subtypes. We compared the operating characteristics of BTD₁₂ with those of the naive design, which is based on the subtype homogeneity assumption, and those of the ITD₁₂ design, which is based on the subtype heterogeneity assumption. The simulation results given in the Supplementary Material show that the proposed BTD₁₂ design strikes a balance between the full-information-borrowing naive design and the no-information-borrowing ITD₁₂ design. However, in this case, one may hypothesize that the performance of BTD₁₂ might be improved by adaptively combining or splitting the cancer subtypes using the latent subgroup membership variable approach of Chapple and Thall (2018). This is a potential area for future research.