The impact of lockdown timing on COVID-19 transmission across US counties

Abstract

Background

Many countries have implemented lockdowns to reduce COVID-19 transmission. However, there is no consensus on the optimal timing of these lockdowns to control community spread of the disease. Here we evaluated the relationship between timing of lockdowns, along with other risk factors, and the growth trajectories of COVID-19 across 3,112 counties in the US.

Methods

We ascertained dates for lockdowns and implementation of various non-pharmaceutical interventions at a county level and merged these data with those of US census and county-specific COVID-19 daily cumulative case counts. We then applied a Functional Principal Component (FPC) analysis on this dataset to generate FPC scores, which were used as a surrogate variable to describe the trajectory of daily cumulative case counts for each county. We used machine learning methods to identify risk factors including the timing of lockdown that significantly influenced the FPC scores.

Findings

We found that the first eigen-function accounted for most (>92%) of the variations in the daily cumulative case counts. The impact of lockdown timing on the total daily case count of a county became significant beginning approximately 7 days prior to that county reporting at least 5 cumulative cases of COVID-19. Delays in lockdown implementation after this date led to a rapid acceleration of COVID-19 spread in the county over the first ~50 days from the date with at least 5 cumulative cases, and higher case counts across the entirety of the follow-up period. Other factors such as total population, median family income, Gini index, median age, and within-county mobility also had a substantial effect. When adjusted for all these factors, the timing of lockdowns was the most significant risk factor associated with the county-specific daily cumulative case counts.

Interpretation

Lockdowns are an effective way of controlling the spread of COVID-19 in communities. Significant delays in lockdown cause a dramatic increase in the cumulative case counts. Thus, the timing of the lockdown relative to the case count is an important consideration in controlling the pandemic in communities.

Funding

The study period is from June 2020 to July 2021. Dr. Xuekui Zhang is a Tier 2 Canada Research Chairs (Grant No. 950231363) and funded by Natural Sciences and Engineering Research Council of Canada (Grant No. RGPIN201704722). Dr. Li Xing is funded by Natural Sciences and Engineering Research Council of Canada (Grant Number: RGPIN 202103530). This research was enabled in part by support provided by WestGrid (www.westgrid.ca) and Compute Canada (www.computecanada.ca). The computing resource is provided by Compute Canada Resource Allocation Competitions #3495 (PI: Xuekui Zhang) and #1551 (PI: Li Xing). Dr. Don Sin is a Tier 1 Canada Research Chair in COPD and holds the de Lazzari Family Chair at the Heart Lung Innovation, Vancouver, Canada.

Research in context.

Evidence before this study

We searched PubMed using the term “coronavirus”, “COVID-19″, or “SARS-CoV-2″ combined with “lockdown”, “sociodemographic factor” or “non-pharmaceutical interventions” for original articles published before May 18, 2021. Similar searches were done in medRxiv, Google Scholar, and the Web of Science.

Previous studies have found that implementation of lockdowns along with other non-pharmacologic interventions (NPIs) reduces the spread of COVID-19 in communities. However, the optimal timing of lockdown relative to the rise in case counts in a community has not been fully explored.

Added value of this study

To the best of our knowledge, this is the first study to use functional principal component analysis (FPCA) to investigate COVID-19 infection trajectories and their relationship with different risk factors and lockdown policies at a county level in a longitudinal manner. We used segmented regression to investigate the effects of lockdown timing on cumulative COVID-19 incidence across the US. We found a critical time point after which delays in lockdown are associated with a rapid spread of COVID-19 in that community. This critical time point occurred approximately 7 days prior to communities reporting at least 5 cumulative cases of COVID-19.

Implications of all the available evidence

Our study suggests that lockdown is an effective policy to reduce case counts of COVID-19 in communities. The inflection point of the relation between lockdown timing and the shape of COVID case trajectories is approximately 7 days prior to a county reporting at least 5 cumulative cases of COVID-19. Thus, earlier lockdown mitigates the spread of COVID-19 in communities; significant delays lead to a rapid increase in case counts. These data will help policymakers to determine the optimal timing of lockdowns for their communities.

Alt-text: Unlabelled box

1. Introduction

Coronavirus disease 2019 (COVID-19) is a global pandemic that has affected over 181 million individuals and killed 3.9 million people across the world as of June 27, 2021 [1]. SARS-CoV-2, the virus responsible for this pandemic, is transmitted through a respiratory route with an average basic reproductive number (commonly denoted as R0) of 2–3 [2]. At this R0, there is an exponential growth in the case counts of COVID-19 in the community, leading to large increases in COVID-19 related morbidity and mortality, which may overwhelm the local health care systems. To reduce COVID-19 transmission, governments around the world have imposed ‘lockdowns’ of their communities [3]. By limiting resident mobility and inter-personal contact, lockdowns along with other non-pharmacological interventions (NPIs) reduce the spread of COVID-19 in communities [4], [5], [6]. However, the timing of these lockdowns has been extremely variable with no clear consensus on when they should be implemented in communities. Here, we used data from over 3,000 counties in the United States (US) to determine the relationship between the timing of lockdowns relative to the first appearance of COVID-19 and the trajectory of COVID-19 spread in these communities.

2. Methods

2.1. Data sources

2.1.1. COVID-19 case counts during the pandemic across the United States (US) counties

We extracted COVID-19 data from the Johns Hopkins Coronavirus Resource Center [7] and analyzed the daily records of cumulative COVID-19 case counts across 3340 counties in the US from 2020 to 01–22 to 2021–01–31. We excluded counties that were not included in the US American Community Survey (ACS) [8] 5-year estimates, leaving 3140 counties in the dataset. We further excluded counties that did not report at least five total cases of COVID-19. The final data contained case counts from 3112 counties.

2.1.2. Demographic factors and lockdown across US counties

We extracted demographic, socioeconomic, and health insurance data for each county from the 2015–2019 US Census (using R package tidycensus [12]). Specifically, we fetched the following parameters (which are detailed in Table S1) from the ACS five-year data profile for each county: socioeconomics (comprising median family income and the Gini Index), demographics (comprising total population, population density, and proportionality of males), health insurance status (private and public coverage of health insurance), household composition (median age), ethnicity, and geographical mobility and mode of transportation. In Figs. S3–S16, we display the relationship of these parameters with the COVID-19 count trajectories and have overlaid these values on a US map in Figs. S17–S30. In addition, we determined “lockdown timing”, which was calculated as the difference in days between the date on which the county experienced at least five cumulative cases of COVID-19 and the date on which the county first initiated a lockdown [13]. Here, we defined “lockdown” as the date on which “stay-at-home” orders were issued in a county. If a county instituted multiple lockdowns during the follow-up period, we only used the first lockdown in our downstream analysis.

2.1.3. Non-pharmaceutical interventions

We also included data on non-pharmaceutical interventions (NPI), which were defined using terms from the Oxford Covid-19 Government Response Tracker (OxCGRT) [3]. We formated the data to enable calculation of the time interval (in days) from the reporting date of a county of 5 or more cumulative cases of COVID-19 to the initiation date of the NPI in question. The NPIs included ‘debt/contract relief’ (government preventing termination of services from missing payments), ‘public information campaigns’ (on COVID-19), ‘testing policy’ (accessibility to COVID diagnostics), ‘contact tracing’ (of identified cases), use of ‘facial coverings’, ‘vaccination policy’ (availability of vaccines), and ‘protection of elderly people’. We excluded NPIs which had more than 30% of missing data. Detailed definitions of NPIs can be found in Table S1.

2.2. Statistical methods

2.2.1. Modeling the spread of COVID-19 over time in the US counties using unsupervised machine learning

We considered the daily cumulative case count of a county as its trajectory over time, and extracted the patterns using a functional principal component (FPC) analysis [9]. First, we realigned the trajectories to ensure that there were at least five cumulative cases at the start of each trajectory. We then investigated the hidden patterns in these trajectories with FPC analysis. The FPC model is given using the following formula:

$$log\left({\mathit{Q}}_{ij}\right)=f_i\left(t_j\right)=\mu \left(t_j\right)+\sum _{k=1}^m{\xi }_{ik}{\varphi }_k\left(t_j\right)$$ (1)

Where ${\mathit{Q}}_{ij}$ is the cumulative case count of the i^th county on the j^th day.

The FPC model mapped these trajectories onto an m-dimensional functional space spanned by m orthogonal eigen-functions ${\varphi }_k\left(\right)$. The eigen-functions are ordered by the proportion of variance in the dataset that can be explained by these functions. Each eigen-function describes how individual trajectory differs from $\mu \left(\right)$, which denotes the average trajectory across all the counties. The coefficient ${\xi }_{ik}$ is the functional principal component (FPC) score, or the coordinate of the ith county in the kth dimension of the functional space. Practically, ${\xi }_{ik}$ describes the strength of the k^th pattern in the i^th county's cumulative case count trajectories. Therefore, the log daily case count trajectory of each county can be modeled as the national average trajectory plus the sum of eigenfunctions (weighted by corresponding FPC scores), as in (1). Müller et al. [9,10] introduced the theoretical details that outline the method by which estimated functions $\mu \left(\right)$ and ${\varphi }_k\left(\right)$ as well as coefficients ${\xi }_{ik}$ are generated. In this work, we estimated these parameters using the R package fdaPACE [11].

2.2.2. Exploring the marginal effect of each risk factor

Using a simple linear regression model, we investigated the unadjusted marginal effects of lockdown timing, characteristics of the counties, and NPIs on COVID-19 transmission across the US. A summary statistics from these linear regression models is provided in Table 2.

Table 2.

The unadjusted relationship of the baseline characteristics of the counties with the COVID-19 spread in these communities.

County Characteristics	Association with the First FPC Score
	Coefficient	P-value	Ref. [2]
Lockdown Slope Before the Inflection Point	0.05069*	2.43E-08*	0.448 *
Lockdown Slope After the Inflection Point	1.95820*	< 2E-16*
Total Population	3.87E-05	5.70E-282	0.33883
Contact Tracing	0.23167	2.53E-163	0.21197
Testing Policy	0.23163	2.60E-163	0.21195
Vaccination Policy	0.22893	3.65E-161	0.20944
Debt/Contract Relief	0.22428	6.07E-155	0.20214
Median Age	−1.8156	2.29E-148	0.19434
Proportion of Asians	343.83	4.19E-143	0.18805
Public Information Campaigns	0.18513	4.24E-134	0.17716
Proportion who Moved within the Same County	328.89	9.24E-116	0.15455
Proportion of Individuals who Used Public Transport	253.39	7.88E-93	0.12541
Proportion of Whites	−41.881	4.94E-74	0.10078
Median Family Income	4.17E-04	8.16E-70	0.095166
Population Density	0.0035699	1.27E-61	0.084159
Proportion with Public Health Insurance	−64.053	2.38E-49	0.067428
Proportion of African Americans	35.071	6.27E-39	0.053
Gini Index	117.79	6.10E-28	0.037569
Proportion of Male	−164.56	1.02E-22	0.030165
Protection of Elderly People	0.027229	9.03E-17	0.021685
Proportion with Private Health Insurance	22.156	4.40E-09	0.010696
Facial Coverings	0.012778	1.94E-06	0.0069405
Proportion of Natives	−16.217	0.0023103	0.002661

Variables are sorted by R². The first FPC score is used as a surrogate for COVID-19 spread across the counties. (*Results from segmented regression model; the rest are from linear regression models).

Fig. 3 shows that the observed relationship between the first FPC scores and the timing of lockdowns was non-linear: its appearance was that of a “hockey stick” with an inflection point indicating a significant change in its slope. Thus, we derived three new variables from the timing of lockdown: a binary indicator of lockdown implementation, a slope before inflection point (denotes the effect of the lockdown timing when implemented before the inflection point), and a slope after inflection point (denotes the effect of the lockdown timing when implemented after the inflection point), and used segmented regression to model this relationship. The inflection point for the lockdown variable was ascertained via the significant change in the slopes before and after the inflection point. The statistical technical details of the segmented model are provided in supplementary document under section “Modeling lockdown effect using segmented regression.”

Fig. 3.

Relationship between the first FPC score and the first lockdown date. The x-axis represents the number of days between the lockdown date and the date on which the county reported at least 5 COVID-19 cases. Positive values denote counties that instituted a lockdown after they reported at least 5 cumulative COVID-19 cases, while negative values denote counties that instituted a lockdown before they reported at least 5 cumulative COVID-19 cases. Each blue point represents data of a US county. The red hockey-stick shape line represents two fitted slopes of a segmented regression model. The vertical green line (at −7.8 days) indicates the inflection point on which the slope of the first FPC score significantly changes (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

2.2.3. Modeling joint effects of all risk factors simultaneously using supervised machine learning

Finally, to explore the joint effects of all risk factors on the first FPC scores, we fitted an elastic net model [14] to these data. Elastic net is a popular machine learning method, which is based on a regularized linear model

$${\xi }_{i1}={\alpha }_0+{\alpha }_1{X}_{i1}+{\alpha }_2{X}_{i2}+{\alpha }_{.}{X}_{i3}+{\alpha }_4{X}_{i4}+\cdots +{\alpha }_p{X}_{ip}$$ (2)

where $\left(X_{i1},X_{i2},X_{i3}\right)$ are derived variables from lockdown information as defined in model (S1) which together represent the effect of lockdown timing, and $\left(X_{i4},\dots ,X_{ip}\right)$ are (p-3) demographic and NPI characteristics of the ith county.

Compared with multiple linear regression, elastic net incorporates various penalties on coefficients and provides better prediction models. First, elastic net can automatically select important predictors in a linear model (2) by automatically assigning a zero coefficient to unimportant predictors via a penalty on absolute values of coefficients. Second, the elastic net penalty addresses the issue of multi-collinearity among predictors, which makes models more reliable than multiple regressions. However, elastic net does not provide confidence intervals for coefficients. To capture the uncertainty of the risk estimates, we generated 95% confidence intervals for each coefficient using a re-sample (bootstrap) approach. Specifically, we sampled the counties for replication 1000 times. Next, we applied an elastic net model to each of these random subsets to generate 1000 sets of estimated coefficients, and then built a 95% confidence interval using these coefficients. Here, we fitted all elastic net models using R Package ‘glmnet’ [15]. Statistical significance was defined by p-value < 0.05. All data analyses were performed using R Statistical Software [16]. The source codes are available to the public by accessing https://github.com/ubcxzhang/COVID.FPCA/. The mathematical details and interpretation of this modeling process are provided in section “Interpretation of fitted Elastic net models” of the supplementary document.

2.3. Role of the funding

The data analysis is conducted using computing resource offered by Compute Canada/West Grid. The sponsor had no role in the design of the study, the collection and analysis of the data, or the preparation of the manuscript.

3. Results

3.1. Functional principal component analysis of COVID-19 case counts

We performed a Functional Principal Component (FPC) Analysis on the trajectories of COVID-19 spread across 3112 US counties. Strikingly, the first FPC explained a vast majority of the total variance (about 92.86%). The first FPC score represents the weighted average of COVID-19 case counts and the weighted changes in the rate of COVID-19 case counts over time (on an exponential scale), with weights based on the first eigenfunction. Thus, we can use the first FPC score to describe the overall severity of the pandemic for the ith county. In section “Interpretation of the first FPC scores” of the supplementary document, we provide the mathematical details to support this interpretation.

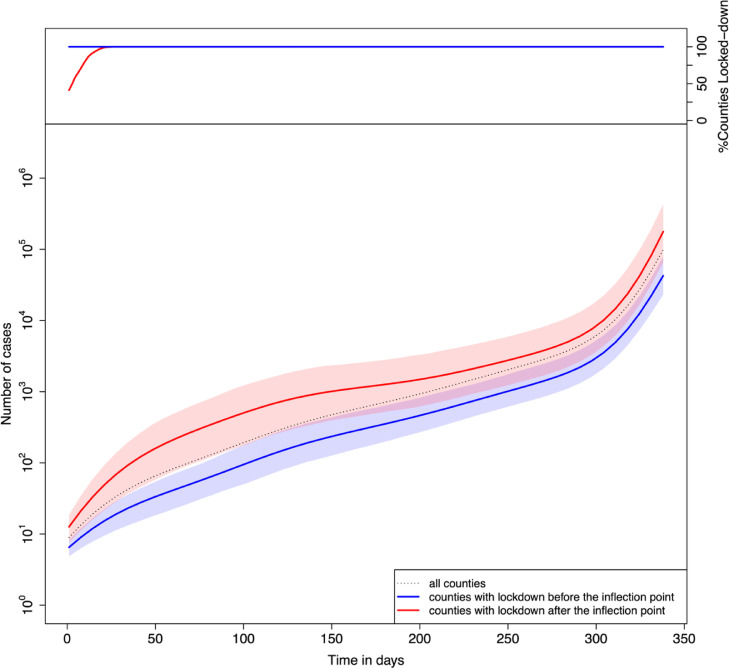
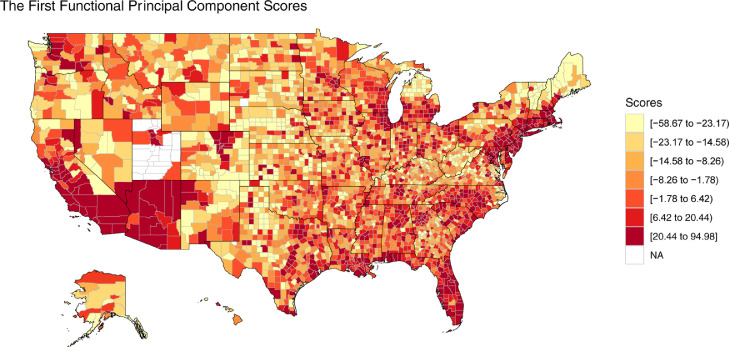
Fig. 1 shows the average trajectory of COVID-19 daily cumulative counts across all US counties, which is denoted by the function $\mu \left(\right)$. In the lower panel, the blue/red curve represents the average COVID-19 case count trajectories of counties that implemented a lockdown before/after the inflection point. The shaded area represents the confidence intervals constructed using the interquartile range (i.e., 25–75% quartiles). An early lockdown (before the inflection point) was associated with a lower case count than the national average across the entirety of the follow-up period; whereas the opposite was true for late lockdowns (defined as occurring after the inflection point). Furthermore, an early lockdown was associated with a slower increase in the rate of COVID-19 counts for the first 50 days of the pandemic. The upper panel shows the percentages of counties which implemented lockdown at each day, grouped by early (blue) or late (red) lockdown. Since we normalized the trajectories by defining day-0 as the day on which a county reported first 5 cumulative cases and “early” versus “late” lockdown was dichotomized based on implementation of a lockdown approximately 7 days prior to day 0, all “early-lockdown” counties were by definition locked-down at day 0. In contrast, the late-lockdown counties did not achieve full lockdown until approximately day 25. The lower panel shows the differences in slopes between red and blue average trajectories over the first 50 days. However, after this period, the two trajectories gradually became approximately parallel, indicating that late-lockdown counties have more cumulative cases across the time range. Fig. 2 shows a heat map of the US according to the FPC score for each county. Since we used the first FPC score as a surrogate variable for the overall severity of the pandemic, the darker colored regions represent a more severe outbreak of COVID-19. Thus, counties in the western and eastern coastal states in general demonstrated significantly higher case counts compared with those in the central states. The most severely affected counties were found in New York, Arizona, Florida, and California.

Fig. 1.

The mean curve of COVID-19 cumulative case trajectories. In the upper panel, the red curve shows the (cumulative) percentages of “late-lockdown” counties which locked down during the follow-up period. Day zero is defined as the date on which a county reported at least 5 cumulative COVID-19 cases. Late-lockdown was defined as implementing lockdown after the inflection point (which occurred approximately 7 days prior to day 0). Blue line denotes “early-lockdown” counties. In the lower panel, dotted curve $\mu \left(\right)$ represents the national average of COVID-19 cases over time. The blue curve represents the average COVID-19 count trajectories of counties that implemented a lockdown before the inflection point, while the red curve represents the average trajectories of counties with lockdown after the inflection point. The shaded area represents confidence bound constructed using interquartile range (i.e., 25−75% quantiles) (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

Fig. 2.

Heat map of the United States (US) according to the first FPC scores of counties.

3.2. The marginal effects of risk factors

We employed a simple linear regression to explore the unadjusted relationships between the cumulative case count trajectories and each potential risk factors. Table 2 summarizes the results, which include regression coefficients, p-values, and the R² statistic. Among the 21 factors we investigated, all of them demonstrated a significant coefficient (p-value < 0.05) for the first FPC score. The marginal R² was moderate for these factors, up to 0.34. The variable ‘Total Population’ (R²=0.339) displayed the strongest association, which was followed by the variable, ‘Contact Tracing’ (R²=0.212). The two most negatively correlated factors were ‘Median Age’ (R²= 0.194) and ‘Proportion of Whites’ (R²= 0.101).

3.3. The impact of implementing a lockdown

Fig. 3 shows the relationship between the first FPC scores and the timing of the lockdown, which displays a strong non-linear relationship. To better characterize this relationship, we used a segmented regression model. Compared with a linear regression model, segmented regression improved the fit of the model (i.e., R²=0.45 for segmented regression vs. R²=0.20 for linear regression). The red lines in Fig. 3 show the segments of a fitted line, whose appearance was a “hockey stick” containing an inflection point. Using time zero as the date on which a county reported at least 5 cumulative cases of COVID-19, we identified day −7.76 (i.e., approximately a week before a county reported at least 5 cumulative cases of COVID-19) as the average “inflection” point (the green vertical line in Fig. 3) in the segmented regression model. We divided the counties into two groups based on whether or not a lockdown was implemented before this inflection point, and compared the underlying demographic and lockdown features of these two groups (Table 1). Note that certain NPIs were negative values because these policies were implemented at an early stage in the pandemic (i.e., before the counties reported 5 or more cumulative cases). The detailed results of the segmented regression model are shown in Table 2. Specifically, the two slopes corresponding to the two segments, ‘Lockdown Slope before the Inflection Point’ and ‘Lockdown Slope after the Inflection Point’ were all positive, corresponding to 0.05069, and 1.95820, respectively.

Table 1.

Baseline characteristics of counties according to implementation of early or late lockdown (defined as whether or not implementation date was before the inflection point, i.e., 7 days before 5 total cases were reported in a county) in the course of the pandemic.

County Characteristics	Early Lockdown (n = 1349)	Late Lockdown (n = 1378)
Total Population (x103)	20.6 ± 21	208 ± 479
Population Density (number of people per sq mile)	64.2 ± 322	543 ± 2660
Median Age (years)	42.9 ± 5.51	39.9 ± 4.71
Median Family Income ($ x103)	61.5 ± 12.3	70.7 ± 19.2
Gini Index	0.441 ± 0.0378	0.453 ± 0.0344
Proportion of Male (%)	50.7 ± 2.76	49.5 ± 1.83
Proportion of Whites (%)	87.4 ± 14.4	77.1 ± 17.4
Proportion of African Americans (%)	5.17 ± 11	14.5 ± 16.8
Proportion of Natives (%)	2.22 ± 7.69	1.1 ± 4.42
Proportion of Asians (%)	0.741 ± 1.72	2.19 ± 3.63
Proportion of Individuals who Used Public Transport (%)	0.438 ± 1.06	1.54 ± 4.44
Proportion who Moved within the Same County (%)	5.62 ± 2.44	6.9 ± 2.6
Proportion with Private Health Insurance (%)	63 ± 10	66.4 ± 9.82
Proportion with Public Health Insurance (%)	42.3 ± 9.09	37.5 ± 8.09
Debt/Contract Relief (days)*	−60.3 ± 45.4	−7.46 ± 8.64
Public Information Campaigns (days) *	−91.4 ± 48.8	−33.3 ± 22.1
Testing Policy (days) *	−117 ± 45.5	−65.2 ± 7.42
Contact Tracing (days) *	−117 ± 45.5	−65.2 ± 7.41
Facial Coverings (days) *	123 ± 143	170 ± 138
Vaccination Policy (days) *	211 ± 45.5	264 ± 9.55
Protection of Elderly People (days) *	−4.44 ± 135	43.6 ± 112

P-values for all variables are smaller than 0.05 based on a Wilcoxon test for differences between early lockdown and late lockdown. Data are shown as mean ± SD.

^⁎days are calculated relative to day 0 (i.e. the date on which counties reported 5 or more cumulative cases of COVID-19). A negative value would indicate that counties implemented these non-pharmacologic intervention (NPI) several days prior to day 0; a positive value would indicate that NPIs were implemented after day 0.

3.4. Joint modeling for all risk factors for COVID-19

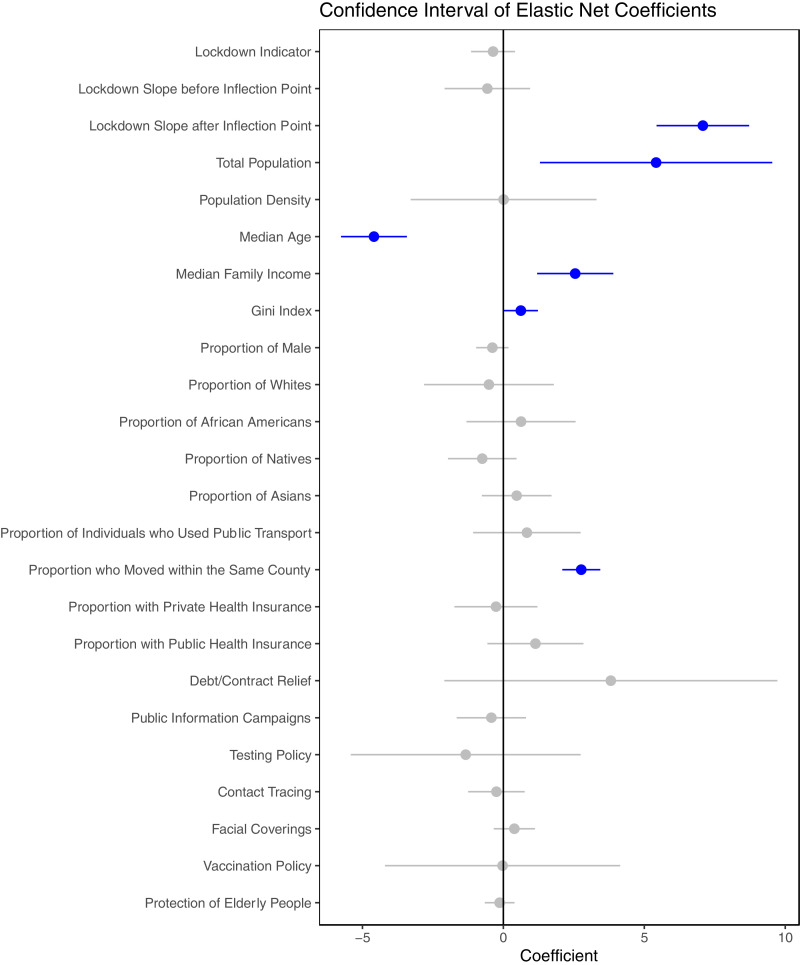
We found that certain risk factors were highly correlated with each other as shown in Fig. S1. As seen in regression models of marginal effects, most of the risk factors were significantly associated with COVID-19 infection. To investigate their joint effects after adjusting for other variables, we used an elastic net model to determine the relationship of the first FPC scores with these predictors. The confidence intervals, obtained from 1000 bootstraps, are shown in Fig. 4 and the mean value and the 95% confidence interval of the model's coefficients are shown in supplementary Table S2. We note that the elastic net models achieved a much better fit with an R² of 0.62, compared with the marginal regression results in which the maximal R² was 0.34 for the first FPC score.

Fig. 4.

The adjusted relationship between standardized characteristics of counties and the first FPC scores, based on results of elastic net models. The effect of every variable is adjusted to other factors listed in the figure. A positive coefficient denotes variables that are positively related to the number of COVID cases. The dot indicates the mean coefficients, and the bar represents the 95% confidence interval. Blue color indicates the significant factors whose 95% confidence interval does not cover 0 (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

We observed that 6 of 24 risk factors demonstrated statistical significance (i.e., their coefficients did not cover zero). For example, ‘Lockdown Slope after Inflection point’ and ‘Total Population’ were positively associated with the first FPC scores, while ‘Median Age’ was negatively associated with the first FPC scores. Other positive risk factors included ‘Median Family Income’, ‘Gini Index’, and ‘Proportion who Moved within the Same County’. Many other factors became statistically insignificant in the joint models.

In the elastic net models, the mean of ‘Lockdown Slope after Inflection Point’ was 1.048 from 1000 bootstraps. This indicates that, after adjusting for other factors, if a lockdown was implemented after the inflection point, there was an exponential increase in the cumulative COVID-19 case counts in the community over the follow-up time. Specifically, model (S5) demonstrates that the changes in the daily cumulative case count are a function of the first FPC scores and the first eigenfunction. For each day of delay in implementing a lockdown after the inflection point, the daily cumulative case count increased on average by 5.80% (range 2.36 to 7.03%). For each week of delay in implementing a lockdown after the inflection point, the daily cumulative case count increased on average by 48.36% (range 17.77 to 60.92%). The timing of the lockdown at the county level explained 45% of the total variance (R² of segmented regression model) in the cumulative case counts of COVID-19 across the communities.

4. Discussion

Lockdowns are an effective way of reducing the reproduction number of COVID-19 and controlling the spread of disease in local communities. However, there is no consensus on when governments should take this action. Here, we found that communities, which implemented the lockdown at or prior to the inflection point (defined as 7 days before the date on which at least 5 cumulative cases were first reported in the community) experienced a slower rise in COVID-19 rates over the first 50 days and a lower cumulative count consistently across all time points during follow-up compared with counties that implemented lockdowns after the inflection point (Fig. 1). In our models, the timing of the lockdown at the county level explained nearly 50% of the total in COVID-19 case counts across US counties, highlighting the importance of early lockdown implementation in controlling the pandemic at the county level.

Our findings extend data from recent cross-sectional studies that have investigated the relationship of COVID-19 spread in communities with their population characteristics and lockdown measures. By examining the temporal patterns of COVID-19 transmission within and across the US, we demonstrated the relationship between the timing of lockdown implementation and the trajectory of COVID-19, independent of other characteristics, within and across US counties using FPC analysis for the first time. We were able to convert the trajectory of COVID-19 spread for each county into a (first) FPC score, which accounted for 93% of the total variance in the COVID-19 infection trajectories across the US counties. This enabled us to use the first FPC score as a surrogate for infection case counts in these counties and model the relationship of the longitudinal COVID-19 infection pattern with the timing of lockdowns, and other risk factors including the use of NPIs, and demographic characteristics of US counties.

Based on an elastic net model of risk effects, we found that the most important factors associated with a rapid spread of COVID-19 at a county level were the timing of the lockdown, and certain characteristics of the counties. For example, counties with a larger population experienced a more rapid rate of COVID-19 transmission compared with smaller counties. The heat map (Fig. 2) reveals that the most populous states, such as New York, California, and Florida, were most impacted by COVID-19. At a city level, Los Angeles had the highest first FPC score, followed by Chicago, Miami, and New York, which all have large populations. Interestingly, counties with a higher median family income and a higher Gini Index (representing greater spread of income inequality) experienced a more rapid COVID-19 surge, which aligns with the findings by Tan et al. [17] Although COVID-19 becomes more severe among older adults, counties with a lower median age experienced more case counts than older counties. These data are consistent with the observation that case counts generally decrease with increasing age in adulthood [18]. Finally, we found that increased mobility within counties is also associated with increased COVID-19 case counts.

There are many definitions of lockdowns [19]. Here, we defined lockdown as the day on which the local government issued a “stay-at-home” order. To evaluate the robustness of our results, we performed several additional analyses using alternate definitions of lockdown (e.g. the date of school closing, workplace closing, cancelation of public events, restrictions on gatherings, etc.). However, the use of alternate definitions did not materially change the primary results. In every case, the analysis showed a non-linear “hockey-stick” relationship between the date of “lockdown” and the cumulative rise in case counts across the US communities, as shown in Fig. S32–S36. Importantly, we found that the definition based on the date of stay-at-home order produced the fewest number of outliers amongst all definitions that were evaluated. Thus, we believe that our a priori decision to use the date of issuance of a stay-at-home order was a reasonable choice for our primary analysis, yielding the most robust data.

Note, Principal Component Analysis (PCA) is a popular dimension reduction method. In this work, however, we used FPC analysis instead of PCA for the following three reasons: (1) The model had to account for differential follow-up time across the counties. This occurred because the date on which 5 cumulative cases were reported for each county significantly differed. Differential follow-up time, however, led to an uneven matrix, preventing the use of PCA. (2) Because FPC analysis considers each trajectory to be a smooth curve, this allows observations to borrow information from their nearby points on the trajectory to improve the quality of results. (3) PCA is not sensitive to the time-order of observations and, thus, not suitable for a “trajectory over time”, which again made it unsuitable for our dataset. In contrast, FPC analysis retains all the information of a time-order dataset, making it a preferred choice over PCA.

In this work, we defined “day 0″ as the “first instance of detecting more than 5 cases”. Our choice of 5 cumulative case counts was based on the fact that with a lower threshold, the uncertainty (or the noise) of the measurement would be significantly increased. On the other hand, we were concerned that a higher threshold cutoff (e.g. 100) may artificially bias the inflection point towards a higher number. For example, if we had used 100-cases to define day 0, we would have discarded all the information collected before 100 cases were reached. Although the choice of 5 was arbitrary, in the literature, we found many incidences where statisticians have chosen 5 as their “magic threshold”. To check for the robustness of the case definition, we repeated our analysis using 3-case and 4-case definitions, and found similar results (available upon request).

There were limitations to the study. First, as this was not a randomized controlled trial, unmeasured confounders could have distorted the overall findings. To minimize this possibility, we evaluated only counties in the US and adjusted for the most important characteristics of these counties using well-curated databases. Second, these data were generated in the US and may not apply to other countries around the world, which may have different characteristics and attitudes and adherence to public health policies such as masking and social distancing. Third, we could not fully quantify the stringency of the stay-at-home orders, or the adherence rate of the residents to the lockdown order across the counties. Fourth, in our analysis, we considered the effects of the first lockdown order for each of the counties. It should be noted, however, that some counties experienced multiple lockdowns during the follow-up period, leading to an “on-and-off” effect. Future studies will be needed to evaluate the effects of multiple lockdowns on communities. Finally, we could not address problems related to the quality of data source such as unexplained bias and unobserved errors in the raw data.

Notwithstanding these limitations, our findings have important public health implications. Local state and municipal governments should issue an immediate lockdown order even when there are a few cases of COVID-19 in their communities (less than 5); any significant delays in lockdown beyond this point are associated with a rapid growth of COVID counts and a higher overall cumulative count trajectory, which will make COVID-19 containment difficult for that community.

Declaration of Competing Interest

Dr. Zhang reports grants from Natural Sciences and Engineering Research Council of Canada, during the conduct of the study; Dr. Xing reports grants from Natural Sciences and Engineering Research Council of Canada, during the conduct of the study; Dr. Sin reports personal fees from GSK, grants and personal fees from AstraZeneca, personal fees from Boehringer Ingelheim, personal fees from Grifols, outside the submitted work; all other authors report nothing.