Longitudinal Harmonization for Improving Tractography in Baby Diffusion MRI

Abstract

The human brain develops very rapidly in the first years of life, resulting in significant changes in water diffusion anisotropy. Developmental changes pose significant challenges to longitudinally consistent white matter tractography. In this paper, we will introduce a method to harmonize infant diffusion MRI data longitudinally across time. Specifically, we harmonize diffusion MRI data collected at an earlier time point to data collected at a later time point. This will promote longitudinal consistency and allow sharpening of fiber orientation distribution functions (ODFs) based on information available at the later time point. For this purpose, we will introduce an approach that is based on the method of moments, which allows harmonization to be performed directly on the diffusion-attenuated signal without the need to fit any diffusion models to the data. Given two diffusion MRI datasets, our method harmonizes them voxel-wise using well-behaving mapping functions (i.e., monotonic, diffeomorphic, etc.), parameters of which are determined by matching the spherical moments (i.e., mean, variance, skewness, etc.) of signal measurements on each shell. The mapping functions we use is isotropic and does not introduce new orientations that are not already in the original data. Our analysis indicates that longitudinal harmonization sharpens ODFs and improves tractography in infant diffusion MRI.

1. Introduction

White matter contains axonal tracts that relay and coordinate communication between different brain regions. Myelination begins in the last trimester with myelin sheaths wrapping around axons and significantly boosting nerve conduction velocity [1]. Rapidly ongoing myelination during infancy leads to dynamic development in verbal, motor, and cognitive functions [2]. As a fatty substance, myelin sheath limits water diffusion in direction perpendicular, but not parallel, to the tracts, causing diffusion anisotropy and giving contrast to diffusion-weighted (DW) images.

Tractography is significantly affected by changes in diffusion anisotropy. This stems from the fact that, in general, tractography methods are designed to traverse areas of high anisotropy and avoid areas of low anisotropy. In the developing brain where the anisotropy is typically low and progressively increases with maturation, far fewer voxels are included in the pathway at birth than at successive time points. As a result, even there is a profusion of tracts in an infant brain, incomplete myelination makes reconstruction of the tracts via diffusion tractography challenging. An often used remedy is to lower the anisotropy threshold to allow a tractography algorithm to generate streamlines that traverse some regions with low anisotropy. This approach, however, might result in spurious streamlines owing to directional uncertainty caused by the lack of anisotropy.

To tackle the problem, we propose in this paper a longitudinal harmonization method to improve tractography for infant diffusion MRI. Based on the method of moments, our approach involves a model-free harmonization strategy that can be applied directly on longitudinal data without fitting of diffusion models. This is achieved with mapping functions that are designed to be smooth (no abrupt changes), one-to-one (topology preserving), non-decreasingly monotonic (contrast preserving), and invertible (data recoverable). The parameters of the mapping functions are determined by matching the spherical moments (i.e., mean, variance, skewness, etc.) of signal measurements on each shell. These functions are applied isotropically and do not introduce new orientations that are not already in the original data. Our analyses indicate that longitudinal harmonization sharpens fiber orientation distribution functions (ODFs) and improves tractography without introducing false-positive streamlines.

2. Methods

In shell-based sampling, the diffusion-attenuated signal S_b is sampled using a set of non-collinear gradient directions with a fixed diffusion weighting (i.e., b-value). The n-th raw spherical moment is defined as

$$E[S_b^n]={\int }_{{\mathbb{S}}^2}{S}_b^n(g)dg.$$ (1)

The spherical mean ($M_{1,S_b}$) and variance ($M_{2,S_b}$) can be defined based on the first and second raw spherical moments as

$$M_{1,S_b}={\overline{S}}_b=E[S_b],$$ (2)

$$M_{2,S_b}=E[{\left(S_b-E[S_b]\right)}^2].$$ (3)

Taking the dataset at a later time point as the reference R and the dataset at an earlier time point as the target T, we want to determine a mapping function f_θ(S) that results in the matching of the two moments:

$$M_{1,R}=E[R]=M_{1,f_{\theta }(T)}=E[f_{\theta }(T)],$$ (4)

$$M_{2,R}=E[{(R-E[R])}^2]=M_{2,f_{\theta }(T)}=E[{\left(f_{\theta }(T)-E[f_{\theta }(T)]\right)}^2],$$ (5)

where $M_{n,f_{\theta }(T)}$ is the n-th moment of the target after mapping via f_θ(S) whereas M_n,T is the moment before mapping. It is shown in [3] that the spherical mean is independent of the fiber orientation distribution and can be used to characterize per-axon microstructural properties. The spherical variance can be seen as a measure of fiber orientation consistency (opposite to fiber dispersion).

To maintain signal contrast, the mapping function must be monotonic. In this work, using the first two moments, we employ a first-order mapping function f_θ={α,β}(S) = αS + β and (4) and (5) can therefore be written as

$$M_{1,R}=\alpha M_{1,T}+\beta \text{and}{M}_{2,R}={\alpha }^2{M}_{2,T},$$ (6)

allowing the parameters to be determined as

$$\alpha =\sqrt{M_{2,R}/M_{2,T}}\text{and}\beta =M_{1,R}-\alpha M_{1,T}.$$ (7)

To ensure that the contrast is not inverted, we constrain α > 0. The estimation of parameter α is problematic in isotropic regions where the variance is a primarily due to noise, resulting in instability in parameter estimation. For greater robustness, we estimate the parameters using regularized least-squares, as described next.

Assuming that the reference and target moment images are spatially aligned, moment matching is performed voxel-wise. For each voxel υ, the mapping parameters are determined by minimizing the cost function J(α(υ),β(υ)) of the unconstrained multivariable optimization problem with Quasi-Newton algorithm:

$$J(\alpha (v),\beta (v))={\Vert \left(\begin{array}{l}{M}_{1,R}\left({\varphi }^{-1}(v)\right)-M_{1,T}\left(f_{\theta =\{\alpha (v),\beta (v)\}}(v)\right)\hfill \\ M_{2,R}\left({\varphi }^{-1}(v)\right)-M_{2,T}\left(f_{\theta =\{\alpha (v),\beta (v)\}}(v)\right)\hfill \end{array}\right)\Vert }_2^2+\psi (\alpha (v),\beta (v)),$$ (8)

where φ(υ) is a deformation field that spatially aligns the reference to the target. The regularizer is defined as

$$\psi (\alpha ,\beta )=\lambda \left\{\left[1-e^{-\frac{{(\alpha -1)}^2}{2}}\right]+\left[1-e^{-\frac{{\beta }^2}{2}}\right]\right\},$$ (9)

where λ is a tunning parameter. The signal S_b(g|υ) at spatial location v and for gradient direction g is harmonized via

$$S_b^{\prime }(g\mid v)=\alpha (v)S_b(g\mid v)+\beta (v).$$ (10)

Note that the mapping does not change with the gradient direction. We found that the first order mapping function is sufficient for our application. Our method allows more sophisticated mapping functions to be used as long as basic properties, such as nondecreasing monotonicity, are met. The parameters, if more than two, can be estimated using higher-order moments. Our method only requires warping of the moment images, but not the DW images, for matching; therefore issues related to signal reorientation [4] can be avoided.

3. Experiments

We study the effects of longitudinal harmonization using both synthetic and real in-vivo baby diffusion MRI data.

3.1. Synthetic Data

We generated multi-shell synthetic data simulating a complex phantom using Phantomas with 90 DW images in each shell (b = 1000, 2000, and 3000s/mm²) and 18 non-diffusion-weighted B0 images [5]. The reference was created using a 27-bundle configuration with λ₁ = 1.7 × 10⁻³ mm²/s and λ₂ = λ₃ = 4.35 × 10⁻⁴ mm²/s to simulate high fractional anisotropy (FA = 0.7). The target was created using only a 8-bundle configuration (subset of the 27 bundles) with λ₁ = 1.7 × 10⁻³ mm²/s and λ₂ = λ₃ = 1.2 × 10⁻³mm²/s to simulate low anisotropy (FA = 0.2). Rician noise was added.

To illustrate the effects of harmonization, we performed global tractography [6] on both unharmonized and harmonized datasets. Figure 1 shows that after harmonization, the streamlines are cleaner and denser with less false positives. Harmonization also increases the anisotropy of the diffusion signal profiles. Table 1 summarizes the Tractometer [7] statistics, indicating that harmonization increases valid connections and decrease invalid connections. With harmonization, the 8 streamline bundles can be fully recovered without any false positives that may be introduced by the reference.

Fig. 1. Synthetic Data.

Tractography results of the 8-bundle phantom (middle) and exemplar diffusion signal profiles (right) before and after harmonization. Note that even though the reference has 27 bundles, harmonization does not introduce any false-positive bundles

Table 1.

Tractometer statistics for synthetic data

	Tracts	VC(%)	IC (%)	NC(%)	$\frac{\mathrm{VC}}{\mathrm{VC}+\mathrm{IC}}$ (%)	VB	IB
Unharmonized	4870	2.5	7.1	90.4	26.04	8	12
Harmonized	8052	11.5	3.2	85.3	78.2	8	9
Reference	10962	12.89	3.22	83.89	80.01	27	127

3.2. Real Data

We used a diffusion MRI dataset of a 9-month old subject as the reference to harmonize the dataset of the same subject collected at 3 months of age. Each dataset consist of 74 DW images distributed on two shells (b = 1500 and 3000s/mm²) and 5 non-DW B0 images. Eddy-current distortion, motion, and susceptibility artifacts were corrected prior to harmonization [8]. The dataset of the later time point was registered to the earlier time point using multi-channel diffeomorphic registration [9] with fractional anisotropy (FA) and B0 images. Signal normalization was carried out by dividing the DW images with the average of the non-DW images.

Diffusion Indices:

Fractional anisotropy (FA), mean diffusivity (MD), per-axon FA (μFA), and per-axon MD (μMD) were compared before and after harmonization. Figure 2 illustrates the effects of harmonization on the indices. The anisotropy of the 3-month dataset increases noticeably after harmonization.

Fig. 2. Diffusion Indices.

Fractional anisotropy (FA), mean diffusivity (MD), per-axon FA (μFA), and per-axon MD (μMD) of the 3-month dataset before (top) and after (middle) harmonization, and the 9-month reference dataset (bottom)

Fiber ODFs:

Multi-tissue constrained spherical deconvolution [10] was performed to estimate the fiber ODFs. From Fig. 3, one can appreciate the increase in sharpness of the FODFs after harmonization. The tissue volume fraction map also reveals greater details with further extension into cortical regions.

Fig. 3. Fiber ODFs.

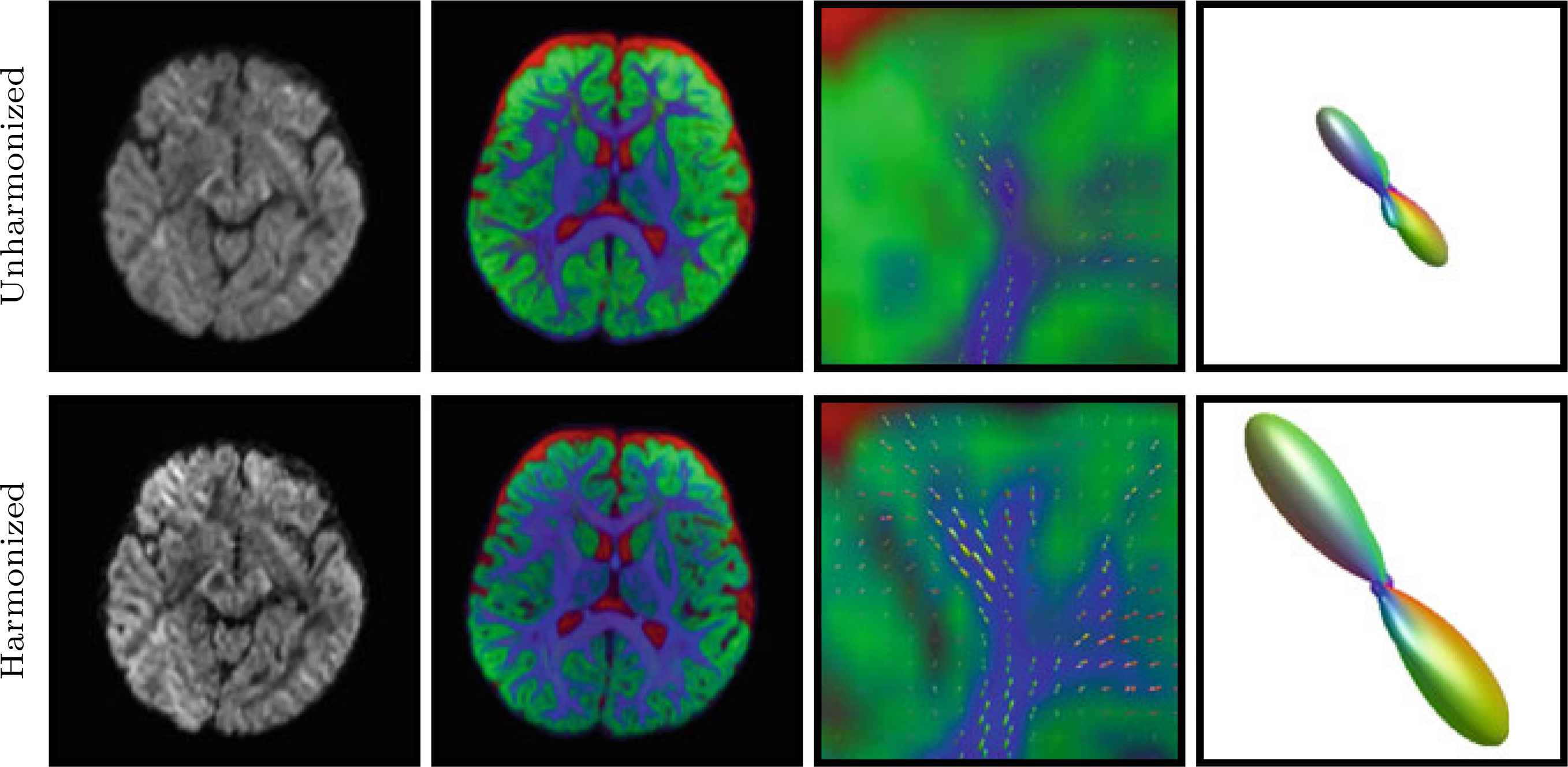
Left to Right: DW image, tissue volume fraction map (Blue: White matter; Green: Gray matter; Red: Cerebrospinal fluid), Close-up view of forceps minor, and an FODF in forceps minor before and after harmonization

Tract Probability:

The tract probability maps shown in Fig. 4 were obtained using tractography with second-order integration over the fiber ODFs [11]. After harmonization, all 20 major tracts described in [12] show increased tract probabilities. Detailed quantitative results are provided in Table 2.

Fig. 4. Tract Probability.

Probability (%) of the presence of a tract at a particular location, determined via probabilistic tractography using unharmonized and harmonized data

Table 2.

Probalility (%) of major tracts before and after harmonization

Tract	Unharmonized	Harmonized
Anterior thalamic radiation (L)	10.79	20.57
Anterior thalamic radiation (R)	8.45	16.37
Corticospinal tract (L)	16.42	22.21
Corticospinal tract (R)	21.38	33.81
Cingulum (cingulate gyrus) (L)	7.63	13.96
Cingulum (cingulate gyrus) (R)	5.40	11.65
Cingulum (hippocampus) (L)	6.65	11.52
Cingulum (hippocampus) (R)	6.45	10.83
Forceps major	14.90	23.56
Forceps minor	12.86	24.03
Inferior fronto-occipital fasciculus (L)	14.24	25.37
Inferior fronto-occipital fasciculus (R)	13.78	23.77
Inferior longitudinal fasciculus (L)	9.06	16.50
Inferior longitudinal fasciculus (R)	12.27	23.57
Superior longitudinal fasciculus (L)	13.36	25.92
Superior longitudinal fasciculus (R)	13.96	25.44
Uncinate fasciculus (L)	10.48	24.25
Uncinate fasciculus (R)	9.76	16.60
Superior longitudinal fasciculus (L)	13.29	25.60
Superior longitudinal fasciculus (R)	12.70	29.82

Tractogram:

Whole brain tractograms were constructed using global tractography [13]. Figure 5 confirms the effectiveness of harmonization as it significantly improved tractography results.

Fig. 5. Tractograms.

The effects of harmonization shown using tractograms

4. Conclusion

We have introduced a model-free approach, based on the method of moments, for longitudinal harmonization. We have demonstrated its effectiveness in sharpening fiber ODFs and in improving tractography in infant diffusion MRI.