Abstract
The availability of the epidemiological data strongly affects the reliability of several mathematical models in tracing and forecasting COVID-19 pandemic, hampering a fair assessment of their relative performance. The marked difference between the lethality of the virus when comparing the first and second waves is an evident sign of the poor reliability of the data, also related to the variability over time in the number of performed swabs. During the early epidemic stage, swabs were made only to patients with severe symptoms taken to hospital or intensive care unit. Thus, asymptomatic people, not seeking medical assistance, remained undetected. Conversely, during the second wave of infection, total infectives included also a percentage of detected asymptomatic infectives, being tested due to close contacts with swab positives and thus registered by the health system. Here, we compared the outcomes of two SIR-type models (the standard SIR model and the A-SIR model that explicitly considers asymptomatic infectives) in reproducing the COVID-19 epidemic dynamic in Italy, Spain, Germany, and France during the first two infection waves, simulated separately. We found that the A-SIR model overcame the SIR model in simulating the first wave, whereas these discrepancies are reduced in simulating the second wave, when the accuracy of the epidemiological data is considerably higher. These results indicate that increasing the complexity of the model is useless and unnecessarily wasteful if not supported by an increased quality of the available data.
Keywords: COVID-19, SARS-CoV-2, Epidemiology, SIR-Type models, Symptomatic and asymptomatic transmission, Disease wave modelling
Abbreviations: SIR (Susceptible-Infected-Recovered), A-SIR (Asymptomatic Susceptible-Infected-Recovered)
1. Introduction
Coronavirus is a member of the Coronavirinae subfamily, Coronaviridae family, and Nidovirales Order [1], which mainly causes infections in the respiratory and gastrointestinal tracts [2]. The genome is a single positive (+) strand RNA of about 30 kb in length (26.4–31.7 kb) that represents the longest known RNA virus. Several factors contribute to their high genetic variability:
-
1.
Infidelity of RNA-dependent RNA polymerase that causes a mutation rate of the order of 1 × 103/synonymous site/year.
-
2.
A random template switching during RNA replication with high homologous genome recombination.
-
3.
A great plasticity and genome modification allowed by the large size of the genome [3].
These three factors led to the generation of a diversity of strains and genotypes, but also allow new species to adopt new hosts and ecological niches, sometimes causing major zoonotic outbreaks with disastrous consequences [4].
The subfamily of coronavirinae includes four genera (i.e., Alphacoronavirus, Betacoronavirus, Gammacoronavirus, and Deltacoronavirus) according to their relationship and genomic structure. The Alphacoronavirus and Betacoronavirus infect only mammals. The Gammacoronavirus and Deltacoronavirus infect birds, but some of them can also infect mammals [5]. Seven different coronaviruses (CoVs) are known to affect/infect humans. Four of them, HCoV-NL63, HCoV–229 V (Alphacoronavirus), HCoV-OC43, and HCoV-HKU (Betacoronaviruses), are responsible for mild respiratory and intestinal infections, but they are considered viruses with low pathogenicity [6]. Instead, SARS-CoV (severe acute respiratory syndrome), MERS (Middle East respiratory syndrome), and SARS-CoV-2 have been linked to epidemic or pandemic events. Based on phylogenetic analysis, all three viruses seem to originate from bat viruses, even if their genomes are remarkably different: SARS-CoV-2 shows about 89% similarity with bat SARS-like CoVZC21 and 82% similarity to human SARS-CoV, and only 50% similarity to MERS CoV [7,8]. They have been classified as Beta coronaviruses, but SARS and SARS-CoV-2 belong to the same lineage B, whereas MERS belongs to lineage C.
SARS-CoV was diffused from 2002 to 2003 in 33 countries with 8096 cases and 774 deaths with a case fatality rate (CFR) of 10% [9].
In 2012, MERS was detected in the Middle East with 2494 confirmed cases and 858 fatal cases with a CFR corresponding to 35% [8,10]. Dromedary camel is the intermediate host of this zoonotic virus, while the bat is considered the origin of the MERS virus. The intra-human transmission is rarely described and this could represent a “plausible” explanation of the limited diffusion of this virus. The clinical symptoms may be asymptomatic, mild, or can lead to severe disease with multiorgan failure. The receptor of MERS-CoV to pneumocytes and epithelial cells is the DPP4, a protein that affects glucose metabolism, T cell activation, cytotoxic modulation, cell adhesion, and apoptosis.
In December 2019, a novel CoV named SARS-CoV-2 (COVID-19 causative agent) emerged in Wuhan, city of Hubei province (China), and transmitted to almost 192 countries around the globe with a CFR of 2.3%. According to the weekly epidemiological update released by the World Health Organization (WHO) on the 29th of December 2020, the total number of infected people had reached 79,231,893 and the death toll had increased to 1,754,754 globally [11]. It represents the fifth pandemic after Spanish flu (1918), Asia flu (1957), Hong Kong flu (1968), and swine pandemic flu (2009), thus the first pandemic which is not related to an orthomyxovirus. Both SARS-CoV-2 and SARS-CoV have the same receptor ACE (angiotensin converting enzyme2), which is expressed on the epithelial cell of the lung, kidney, heart, and liver. The attachment of S glycoprotein of ACE2 can cause the loss of cylia, squamous metaplasia, and an increase in macrophages in the alveoli that cause damage to the lung [12]. Biophysical and cryo-EM structure revealed that the affinity of S protein to ACE2 is 10–20 times more contagious for SARS-COV-2 than for SARS-CoV [12,13]. SARS-CoV-2 can not only damage the human lungs but can also attack many other organs, including the gut and blood vessels, thus presenting different signs and symptoms [14].
Many similarities had been observed between SARS-CoV and SARS-CoV-2. Both viruses have a median incubation time of about 5 days (95% CI 5.3–19 days). The progression to acute respiratory distress syndrome occurs approximately around 8–20 days after the onset of first symptoms, whereby lung abnormalities on chest CT (Computed Tomography) show a remarkable/notable severity approximately 10 days after the initial onset of symptoms [15,16], moreover these two viruses possess a significant inter-human transmission and not only on animal-humans. However, several differences should be mentioned in order to understand the wide diffusion of SARS-COV-2 and the high number of deaths it caused:
-
1.
SARS-Cov-2 originated/diffused in a city, Wuhan, which accounts for more than 11 million people, and it spread mainly in the community and not only in health care.
-
2.
High transmission of infection by asymptomatic subjects. Several studies have indicated that asymptomatic patients can transmit SARS-CoV-2 virus to others [[17], [18], [19]], while this evidence lacks in SARS infection. Asymptomatic COVID-19 infectives include both asymptomatic and pre-symptomatic infected people. Those that, even if resulted positive to the reverse transcription-polymerase chain reaction (RT-PCR), never developed any signs or clinical symptoms of COVID-19 are considered asymptomatic infectives. Approximately 60% of COVID-19 cases may have no symptoms or mild symptoms [20]. SARS-Cov-2 viral load in upper respiratory specimens is almost as high in asymptomatic as symptomatic infections [21], indicating that people without symptoms have a strong ability to transmit the virus to others [22]. In a care home in Boston among 408 residents tested for SARS-CoV-2 by RT-PCR, 87.8% were asymptomatic, demonstrating that symptomatic screening may not be an effective way to prevent large clusters of infection [23]. Moreover, although many detection methods are available, individuals with a “window period” of COVID-19 infection could be missed, and up to 29% of patients could have an initial RT-PCR false-negative result [24]. This suggests that a large portion of asymptomatic infections may be going undetected.
3. Different values of the basic reproduction number (R0). It is a key factor of pandemic spread describing the intensity of the infectious disease outbreak. R0 describes the average number of secondary cases generated by an initial index case in the inherent infectiousness of a pathogen. Its value also depends on the environmental conditions, host contact behaviours, and other factors that influence the virus transmission. The value of R0 is notoriously tricky to nail down and its estimation remains still controversial, as witnessed by the broadly and relentless scientific production recently published on this issue. In particular, some studies showed that after 6 months of the outbreak the R0 value oscillated between 1.3 and 7.7, a range wider than other recent pandemic and it reached 13.3 in nosocomial structures [25]. Meanwhile, other studies reported that the R0 value of SAR-CoV-2 oscillated from 0.5 to 2.5 within the time window from March to May 2020 in Italy [26] and was predicted to be equal to 1.98 in October 2020 in Italy [26]. Here, we propose a novel methodology to estimate R0 that shows how its value oscillates between 0.5 and 8 in the time frame from the 27th of February 2020 to the 28th of February 2021. SARS showed an R0 ranged from 2 to 5 [27].
All these considerations lead to the conclusion that it is essential to assess the impact of countries’ strategies since the risk of nosocomial spread may be much higher (Table 1 in Ref. [25]).
Table 1.
Initial configuration for the SIR model.
| Initial parameters | Value | Constraints interval |
|---|---|---|
| 0.5 | (0,1) | |
| 0.5 | (0,1) | |
| Initial condition | ||
| N | 60′317′116 | |
| S | ||
| I | ||
| R | 0 |
Several mathematical models have been produced to forecast the COVID-19 epidemic evolution. In the following, we present a brief discussion of the most popular ones along with their basic assumptions and limitations.
Among simpler models, the deterministic Susceptible-Infected-Recovered (SIR) models consist of a set of ordinary differential equations where control parameters are time-independent [28]. In the broad class of SIR-based models, Anastassopoulou et al. [29] proposed a Susceptible–Infected–Recovered–Dead (SIRD) model to estimate the associated per day infection mortality and recovery rates in the Hubei province of Wuhan in China, based on the publicly available epidemiological data from the beginning of January 2020 to the beginning of February 2020; whereas Fanelli et al. [30] developed a SIRD model in combination with mean-field kinetics to calculate the high and the time of the peak of confirmed infected individuals in China, Italy, and France using as model fitting period the time window from the end of January 2020 and the middle of March 2020. The main limitation of these models relies on the intrinsic nature of the standard SIR model that disregards the presence of asymptomatic infectives, being undetected and thus unregistered by the healthcare systems, especially during the early epidemic stage. To overcome this shortcoming, the author of [31] developed a SIR-type model variant, called A-SIR, which explicitly considered the presence of a large set of asymptomatic infectives. Specifically, the author studied the early phase of the COVID-19 epidemic in Northern Italy in terms of the SIR and A-SIR models, by fitting the models’ parameters based on the period of first ten days of March, and considered how the models with such parameters were performing in predicting the evolution for the subsequent weeks. The author found that the dynamics of the two models significantly differed, specifically with the A-SIR model resulting much better in predicting the evolution of the first wave of infection [31].
Of course, the deterministic nature of these SIR-type models disregards the diffusion of the uncertainty in the considered variables and therefore does not allow to get an estimate of the fluctuations in the number of hospitalized patients or to capture changes in disease dynamics. To overcome this limitation, more complex models have been proposed [[32], [33], [34], [35]]. They mainly focused on exploring possible future epidemics scenarios of the long-term behaviour of the COVID-19 epidemic in order to assess the probability of further waves of infection [[33], [34], [35]]. Among them, Faranda and co-authors [33] proposed a stochastic Susceptible-Exposed-Infected-Recovered (SEIR), which consists of a set of ordinary differential equations where control parameters are time-dependent and modelled via a stochastic process. They also introduced the lockdown measures in the model parameters to avoid an overestimation of the number of reported infected individuals (as well as the number of deaths). This choice was raised from the observation that countries like Italy and France, faced a long phase of lockdown with severe restrictions in mobility and social contacts, managed to drastically reduce the actual number of COVID-19 infections. By studying the period from the 27th of December 2019 to the 11th of May 2020 for France and from the 22nd of December 2019 to the 18th of May 2020 for Italy, the authors showed that their model was capable to well reproduce the behaviour of the first wave of infections and to provide an estimate of COVID-19 prevalence consistent with a-posteriori estimation. After the lockdown confinements were released (corresponding to the 11th of May 2020 for France and to the 18th of May 2020 for Italy), they also modelled three different future epidemics scenarios by choosing specific fluctuating behaviours for R0: one where all restrictions are lifted (back to normality); one where strict distancing measures are taken; one where the population remains mostly confined (partial lockdown). They concluded that observing or not the second wave of infections strictly depends on the value of R0 and on the presence or not of super-spreaders: the higher R0, the lower the ability to control the number of infections in the epidemics. Similarly, if super-spreaders are particularly active, the infection counts are difficult to control and a second wave can be triggered more easily. In particular, for what concerns modelling future dynamics of epidemic evolution for Italy, the back to normality scenario predicted the second wave of infections, peaking three months after the initial lockdown measures were released (more or less around the 4th of July 2020) and whose estimated peak intensity was about five millions of people. This would have meant reaching herd immunity by the summer, which is instead far from being achieved yet. The distancing measures scenario produced a second wave mostly similar, in terms of intensity, to the first wave, but occurring later (more or less around the 26th of August 2020); whereas the third scenario, in which partial lockdown measure were taken, did not produce a proper wave of infections.
Among more complex models, where the complexity relies on the number of variables considered rather than the model itself, we recall the recent works [34,35] that extended the standard version of the SIR model to include patients taken to hospitals or to intensive care units. In particular, the authors of [34] categorized infectives in “severe” cases requiring hospitalization, and “non-severe” cases presenting infection with mild symptoms seeking or not medical care before recovery. They calibrated the model by using epidemiological data of the early epidemic stage for Washtenaw County (from the 8th of March 2020 to the 19th of May 2020) and found that the simulation fitted well against the real data in the first wave of infection. Then, they simulated a nine-month time frame beginning on the 8th of March 2020 by considering two distinct scenarios, where both the timing of lifting ‘stay-at-home’ restrictions and the level of casual contacts after reopening were left to vary. Both situations predicted that a second wave would occur in the summer thus anticipating the time of the real peak that occurred in autumn.
Likewise, the author of [35] categorized infectives according to a strong or weak immunity system. They calibrated the model by using epidemiological data of the early epidemic stage for Iran (from the 22nd of January to the 25th of June 2020) and, once again, they found that the simulation fitted well against the real data in the first wave of infection. They predicted a second wave peaking on the 23rd of December 2020 and 25th of December 2020 for the two classes of infected, respectively, thus delaying the time of the real peak that occurred in November. They also showed that decreasing the percentage of people with a weak immune system led to a further delay in the peaking time, showing that their model is very sensitive to the fluctuations of this variable.
Finally, Fokas et al. [36] proposed a novel methodology for predicting the time evolution of COVID-19 infection, exploiting two different approaches: one making use of appropriate mathematical models based on ordinary differential equations and one employing deep learning networks. By comparing the results obtained by applying their models to COVID-19 epidemic data of Italy, Spain, France, Germany, USA, and Sweden countries, the authors established that the two approaches yielded very similar predicting performance.
One of the principal difficulties with all of the above-mentioned mathematical models in both fitting the real dynamics of the COVID-19 infection and predicting its future evolution, is related to limitations that reflect the poor quality and incompleteness of the data available, especially during the first stage of the pandemic. Moreover, the lack of recurring patterns and the marked heterogeneity of the data, limit the reliability of advanced techniques such as ‘deep learning’ which usually require a significant amount of homogeneous and structured data (possibly with a priori knowledge of the nature of the data) to effectively complete the training stage.
Here, in the tricky effort of simulating the dynamics of the COVID-19 pandemic, we had to face two fundamental problems: 1) selecting the best methodology suitable to pursue our goal; 2) selecting the more reliable data for calibrating the model.
For what concerns the first challenge, we chose to stick to deterministic SIR-type models, fueled by the idea that what is really important is the result and not the method for obtaining it. In fact, even if more complex models can give the illusion of realism, still continuing to miss key aspects of biology that are harder to be spotted, they need to introduce additional parameters, which can barely be inferred by the data, at the present stage. On the other hand, simpler models may provide less valid forecasts because they cannot capture some human characteristics, as well as time-varying characteristics of the infectious disease spread. However, a simple and easily comprehensible methodology is preferable to more complex and less intuitive mathematical methods (i.e. a problem-solving principle also known as Occam's razor), when the latter are not justified by the available data and by an improvement in the performance.
For what concerns the second challenge, to estimate the models’ parameters, we used real data of early stage of infection in Italy (from the 27th of February 2020 to the 30th of April 2020), and then we simulated the evolution of infection for the subsequent 240 days (about 32 weeks) up to the 27th of September 2020. Hence, in order to simulate the next phase of infection corresponding to the second wave, we used the same time frame as before but starting from the post-lockdown period (from the 29th of September 2020 to the 30th of November 2020), when data were more accurate and reliable with respect to ones of the early stage of infection, and then we simulated the evolution of infection for the subsequent 90 days (about 12 weeks) up to the 28th of February 2021.
Basically, we started from the simplest standard SIR model and then we compared its outcomes with the ones resulting from the more sophisticated A-SIR model proposed in Ref. [31], which explicitly takes into account the presence of a large set of asymptomatic infectives as further fuel to the spread of infection. Then, we also applied both models to study the COVID-19 epidemic dynamic in other countries (i.e. Spain, Germany, and France), which we selected as, similarly to Italy, they faced a long phase of lockdown with severe restrictions in social contacts and mobility, managing to drastically reduce the number of daily COVID-19 infections, and released almost simultaneously lockdown measures.
Our goal was to assess the performance of both models in predicting the first and second wave of infection, separately, with data reflecting the enforcing/relaxing of confinement measures by the countries we studied. Yet, we aimed to verify whether the conclusions drawn up by the authors of [31] continued to hold even when the quality of the data is higher as the case of the second wave of COVID-19 infection. To complete the analysis, we proposed here a new methodology to evaluate the basic reproduction number R0 and discussed its trend over time during the whole pandemic evolution also with respect to the previous parametric models.
The SIR and A-SIR models presented here to study the epidemic dynamics in Italy, Spain, Germany, and France can be of course applied to many other countries around the world, and this is the reason why we publish the code of our analysis alongside the paper. In particular, we implemented both models (SIR and A-SIR) in the freely accessible and open-source R language environment. Code repository is accessible through GitHub at https://github.com/sportingCode/COVID-19_dynamicsSimulation.git and is targeted to a general audience of non-expert users thus enabling other researchers to further develop and extend the source code.
2. Results
2.1. The SIR model
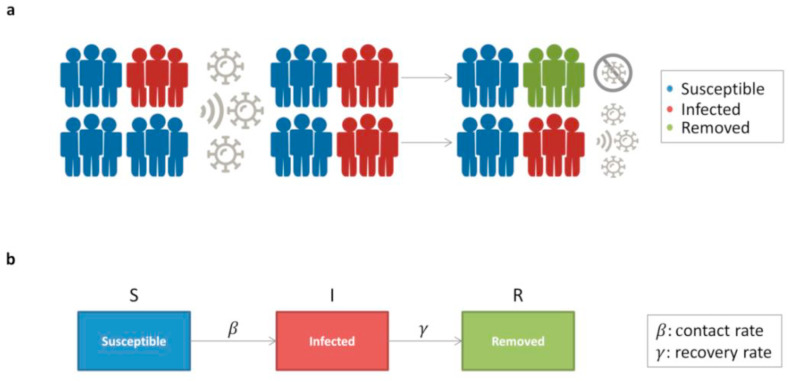
The mathematical modelling for the dynamics of an infective epidemic started with the pioneer Kermack-McKendirck model [28], which provided the basis for a variety of widespread deterministic compartmental models, known as SIR (Susceptible-Infected-Recovered) models. The standard SIR model describes a homogeneous and isolated population of N individuals by partitioning them into three classes: each individual can be either susceptible (S), infected and infective (I), or removed (R) from the epidemic dynamics (i.e., either recovered, dead, or isolated). Denoting by S(t), I(t), and R(t) the populations of these classes at time t, by assumption, S(t) + I(t) + R(t) = N for all t (Fig. 1 ).
Fig. 1.
SIR model. a) Infection spread scenario. At the initial condition, the total population is composed of a percentage of infected individuals (red) and the remaining one of susceptible individuals (blue). Upon exposure, a percentage of susceptible became infected, with an initial probability = 0.5; then, a percentage of infected die or recover and then became removed (green), with an initial probability = 0.5. Infected individuals can still spread the infection, while removed individuals are no longer susceptible to infection. b) Model flow diagram. Upon exposure, individuals progress from susceptible (S) to infected (I) with a contact rate. Then, infected individuals that die or recover will be removed (R) with a recovery rate .
The model is described by the following equations:
with the and time-independent parameters, describing the contact rate and the removal rate, respectively. These parameters depend both on the characteristics of the pathogen and on social behaviour. For instance, a prompt isolation of infected individuals is reflected in increasing , whereas a reduction of social contacts is reflected in decreasing .
The following parameter, known as the basic reproduction number,
has a special relevance since it estimates how many new infections are originated from a single infective in the initial phase of the epidemic [37,38]. When the infection will be able to start spreading in a population, whereas if , the infected people start to decrease and the epidemic will stop.
The assumptions of the SIR model are the following:
-
-
the population is constant, thus disregarding deaths and new births,
-
-
the population is isolated and homogenous, with permanent immunity of individuals who have been infected and recovered,
-
-
an infected individual is immediately infective.
Since the SIR equations are nonlinear, it is impossible to figure out an analytical solution for them. Thus, they have to be numerically integrated as long as the value of the model parameters and the initial conditions (i.e., the number of actual infected individuals) are known. Unfortunately, this is not the case for the new coronavirus responsible for the COVID-19. In fact, even if we have one year of worldwide observations, data are different in each country and cannot be pooled together to have wider statistics. They depend not only on the pathogen agent, but also on the social structure and organization of the country, e.g., on its population density, restrictive measures, and sanitary system; things that are specific to each country. Moreover, even within the same country, the containment measures based on social distancing taken by the Government differ between the first and the second phase of the pandemic. Thus, we cannot use data from the first epidemic wave to estimate the parameters describing the second wave, but we have to perform a wave-dependent model fitting to properly estimate the and parameters (and hence ) that will be thus specific for each phase.
In particular, we set as time zero (t0) of the simulation for the first-wave modelling the day after that 655 cases were reported in Italy (the 27th of February 2020). This roughly corresponds to the moment when the infection starts to spreads more and more rapidly and the curve of infected individuals begins its relentless exponential growth. For the second-wave modelling, we had to set the starting point of the simulation (t0) when the course of the infected curve closely resembles this condition that approximately corresponds to the 29th of September 2020. For both situations, we concentrated on a period of about two months (64 days) during the growth phase of the infected curve starting from the time zero and immediately before peaking.
Then, we assumed that at the initial time (t0) the event of individuals becoming infective occurs with the same probability of becoming recovered (i.e., and were both set to 0.5), that is, an individual could be either infected or recovered with the same initial rate. This choice does not take into account an increased risk factor influenced by age and/or underlying comorbidities, such as hypertension, diabetes mellitus, cardiovascular disease, or healthy condition of immunocompromised people [39]. The and parameters were then varied in the range (0–1).
For the definition of (i.e., infected at time zero) see the text.
As the initial uninfected population N, we used the population of Italy in January 2020 according to the Italian National Institute of Statistics [40], while as the initial infected people (i.e., infected at time zero) we considered the registered infected people in Italy on the 27th of February 2020 for the first infection wave (i.e., 593 infectives) and on the 29th of September 2020 for the second infection wave (i.e., 50′630 infectives). The initial conditions are reported in Table 1.
In order to determine the best fitting for the model parameters, we minimized the residual sum of squares (RSS) defined as:
where I(t) is the number of people in the infectious class I at time t, and is the corresponding number of cases as predicted by the SIR model. To find the values of parameters that give the smallest RSS, we used the optimization method of Byrd and co-authors [41]. The optimization algorithm converged within 100 iterations and the first and second wave-modelling resulting values for the optimized parameters are reported in Table 2 .
Table 2.
Parameters for the SIR model obtained through the fit of I(t) for the first wave and second wave.
| Estimated Parameters | First wave | Second wave |
|---|---|---|
| 1 | 0.44 | |
| 0.90 | 0.37 | |
| 1.11 | 1.18 |
We found in both cases that R0 was slightly above one - say around 1.1 for the first wave and around 1.2 for the second wave – indicating ongoing transmission at a steadily increasing rate over the period between the two waves. This moderate growth of about 10% can be explained by the inclusion in the real count of infected, during the second phase of infection, of a percentage of detected asymptomatic infectives, being tested due to close contacts with swab positives and thus registered by the health system. Since they do not think to be sick and therefore do not self-isolate, asymptomatic people come into contact with more people than symptomatic individuals leading to an increase of the actual value of R0. It is, therefore, reasonable to think that this percentage was not included in the count of the infected in the first phase of the epidemic, when the priorities of the national health system, heavily struck by COVID-19, were to deal with the emergency and swabs were made only to patients with severe symptoms taken to hospital or intensive care units.
Despite the slight discrepancies in the prediction of R0 in the two phases of infection, the estimates of the and parameters during the first and second wave of infection appear to differ substantially. In fact, all individuals who come into contacts with the virus become symptomatic infected () and 90% recovered () as predicted from the model during the first phase, whereas the model predicts 44% of individuals become symptomatic infected () and 37% recover () during the second phase.
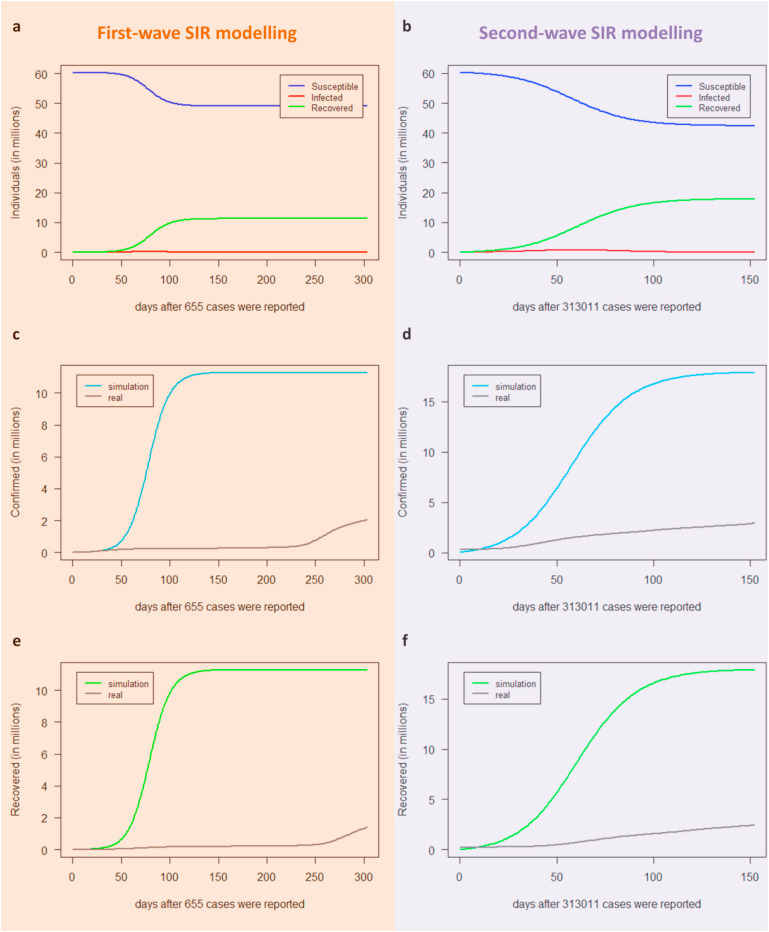
By using the optimal estimated parameters (Table 2), we run the model to simulate the behaviour of the epidemic dynamics in Italy during the first and second infection wave for 304 days and for 153 days starting from time zero, respectively. The first and second-wave modelling results as a function of the number of days after the day corresponding to point zero (t0) are shown (Fig. 2 ). We found that the SIR model performed poorly in simulating the first epidemic wave. In fact, both the number of infectives and the time before the epidemic peak - so the time available to prepare the health system to face it - were over-estimated (Fig. 2a). As already recalled, this could be due as, during this phase when the quarantine measures were adopted, the model's parameters were estimated by epidemiological data based only on registered infectives needing hospital care (thus mostly symptomatic), which were only a small part of the actual infected people, and thus the estimates of the parameters could be largely different from the true ones.
Fig. 2.
Predictions for the infectives I(t) provided by the SIR model for the first (a) and second wave (b) in Italy. The infected individuals predicted by the SIR model (red line) are plotted as a function of days together with the real observed infected people (grey line). The dark blue points represent real data used to estimate the optimal parameters for the best fitting, i.e. the cumulative number of individuals reported to be infected in Italy up to the 30th of April 2020 after the day that 655 cases were reported (27th of February 2020) for the first peak (a) and from the 29th of September 2020 up to the 30th of November 2020 for the second peak (b).
On the other hand, the SIR analysis performed quite well when simulating the second epidemic wave (Fig. 2b). In this period, the number of actual infective people was more realistic and included not only hospitalized patients (which are by definition symptomatic) but also at least a part of detected asymptomatic infectives that were tested due to contacts with known infectives. It's worth noting that the number of infectives when starting to simulate the first wave is 100 times lower than the one at the beginning of the simulation of the second wave, leading to a delay in starting the exponential growth (Fig. 2a).
Yet, the three classes of individuals predicted from the SIR model as a function of the number of days after the day that epidemic broke out for both the first and the second wave of SARS-CoV-2 infection are shown (Fig. 3 ). We found that the number of people not touched by the epidemic wave, so still in danger if a further wave arises, was over-estimated (blue curves in Fig. 3a–b); whereas the SIR model expected a much greater part of the population than reality to go through symptomatic infection and then to recover (Fig. 3c–f). This could be due to the actual number of both confirmed and recovered people (grey lines in Fig. 3c–f) that did not include asymptomatic people, mostly passing unnoticed through the infection and posing a serious threat to public health.
Fig. 3.
Predictions for the three classes provided by the SIR model for the first wave (a-c-e) and the second wave (b-d-f) in Italy. The model simulates the long-term behaviour of the epidemic dynamics in Italy, i.e. 304 days after the 27th of February 2020 (a-c-e) and 153 days after the 29th of September 2020 (b-d-f) when the epidemic broke out for the first and second wave infection, respectively. Blue lines represent susceptible S(t), red lines represent infected I(t), green lines represent recovered R(t), turquoise lines represent confirmed individuals predicted by the SIR model, grey lines correspond either to the actual registered confirmed cases in Italy (c–d), or to the actual registered recovered people in Italy (e–f). A model with asymptomatic infectives: the A-SIR model.
There is increasing evidence that one of the main difficulties in trying to control the ongoing COVID-19 epidemic is the presence of a large cohort of asymptomatic infectives. In fact, at the early stage of a pandemic the registered infectives, those known to the national health systems and thus isolated and monitored, are only a part of the total pool of infectives.
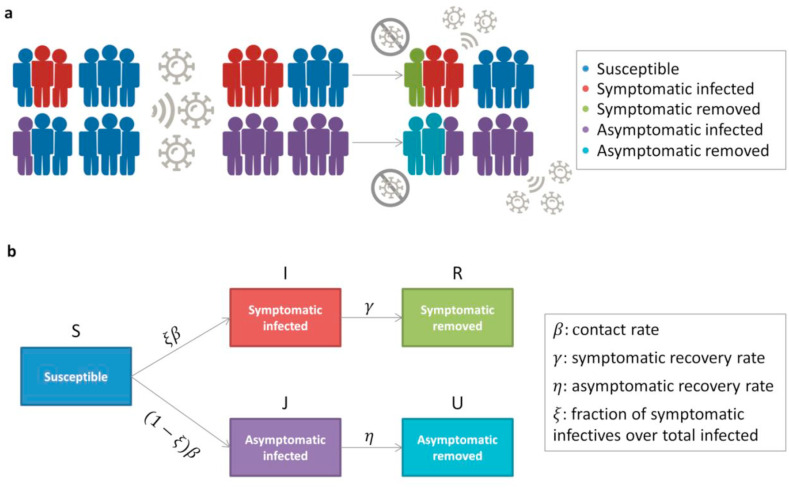
In order to investigate how the presence of a large class of asymptomatic infectives can affect the dynamics within a SIR-type framework, we applied a variant of the SIR–type model, called A-SIR [31], which takes explicitly into account asymptomatic people and the long-time asymptomatic spend being infective and not isolated. In the A-SIR model, each individual can belong either to the susceptibles class S(t), to the two classes of infected and infective people: symptomatic I(t) and asymptomatic J(t); or to the two classes of removed people: symptomatic removed R(t) and asymptomatic removed U(t), mostly passing unnoticed through the infection (Fig. 4 ).
Fig. 4.
A-SIR model. a) Infection spread scenario. At the initial condition, the total population is composed of a percentage of symptomatic infected (red), of asymptomatic infected (purple) that are assumed to be half of the symptomatic ones, and the remaining one of susceptible individuals (blue). Upon exposure, the percentage of susceptible becoming asymptomatic infected (purple) is greater than the one of becoming symptomatic infected (red); then, asymptomatic and symptomatic infected die or recover and thus become removed (light blue or green) with the same initial probability . Infected individuals can still spread the infection, while removed individuals are no longer susceptible to infection. b) Model flow diagram. Upon exposure, individuals progress from susceptible (S) to symptomatic infected (I) with probability ξ and to asymptomatic infected (J) with probability (1-ξ), both with the same contact rate. Then, symptomatic infected individuals that die or recover will be removed (R) with a recovery rate ; whereas, asymptomatic infected individuals that die or recover will be removed (U) with a recovery rate.
The model is described by the following equations:
with the parameter describing the contact rate (as for the above discussed SIR model), the parameters and describing the recovery rate at which symptomatic and asymptomatic people are removed from the epidemic dynamics, respectively; and the parameter ξ describing the fraction of symptomatic patients over the total of infectives.
The assumptions of the A-SIR model are the following:
-
-
the population is constant, thus disregarding deaths and new births,
-
-
the population is isolated and homogenous, with permanent immunity of individuals who have been infected and recovered,
-
-
an infected individual is immediately infective,
-
-
both classes of infected people are infective in the same way,
-
-
an individual who gets infected belongs with probability ξ to the class I(t) and with probability (1-ξ) to the class J(t).
To obtain the best fit of the A-SIR parameters, we used the same procedure described for the SIR model with the initial configuration reported in Table 3 .
Table 3.
Initial configuration for the A-SIR model.
| Initial parameters | Value | Constraints interval |
|---|---|---|
| 0.5 | (0,1) | |
| 0.5 | (0,1) | |
| η | 0.5 | (0,1) |
| ξ | 0.15 | (0.1,0.3) |
| Initial condition | ||
| N | 60′317′116 | |
| S | ||
| I | ||
| J | ||
| R | 0 | |
| U | 0 |
For the definition of (i.e., infected at time zero) and see the text.
In particular, we set the same time zero (t0) of the simulation as for the SIR model, both for the first and second wave. That is, for the first-wave modelling t0 was set to the day after that 655 cases were reported in Italy (the 27th of February 2020), which corresponds to the moment when the infection starts to spread more and more rapidly, and the curve of the infected begins to sharply rise. For the second-wave modelling, t0 was set to the 29th of September 2020, which approximately corresponds to the moment when the course of the infected curve closely resembles the condition observed for the first wave. For both situations, we concentrated on a period of about two months (64 days) during the growth phase of the infected curve starting from the time zero and immediately before peaking.
Then, we assumed that at the time zero (t0) the event of individuals becoming (a)symptomatic infective occurs with the same probability of becoming (a)symptomatic recovered (i.e., , , and η were set to 0.5), that is, an individual could be either infected or recovered with the same initial rate. Then, the parameters , , and η were varied in the range (0–1).
Instead, the estimate of the fraction of symptomatic infectives ξ is part of an ongoing and heated debate, as witnessed by the huge number of recently published studies on this topic [19,31,[42], [43], [44], [45]]. During the early phase of pandemic, in the first infection foci in Italy (i.e., Vo’ Euganeo, near Padua), a significant number of asymptomatic infectives was observed when the whole population (about 3000 people) were tested twice – at one week distance – for the virus [42]. Even the initial estimates produced by the MRC Centre for Global Infectious Disease Analysis of the Imperial College of London were that the registered infectives would be between 1/3 and 1/4 of the actual infectives [45], and later the British Government scientific advisers claimed that this ratio could be as little as 1/10 [46]. In addition, the estimate provided by Li et al. [19] was a ratio of about 1/7 of detected infections, whereas other studies suggested that the fractions of undetected infections could be even higher [43,44]. Furthermore, the author of [31] confirmed the early estimate by the British Government scientific advisers [46], estimating that 10% of infectives in Italy was symptomatic. In accordance with the above discussed, we chose an arbitrary (but realistic) initial value of ξ equal to 0.15 and we constrained it in the range (0.1–0.3).
As for the SIR model, as uninfected initial population N, we still assumed a constant population equal to the population of Italy in January 2020 according to the Italian National Institute of Statistics [40]. As the number of symptomatic infected at time zero (), we set the cumulative number of infectives registered by the Italian healthcare system on the 27th of February 2020 for the first infection wave (i.e., 593 infectives) and on the 29th of September 2020 for the second infection wave (i.e., 25′315 infectives). Given that the number of asymptomatic infectives is not ascertained, setting their initial number is not trivial. We assumed that at time zero they were a fraction of the total infectives registered by the Italian healthcare system. Then, we chose an arbitrary value of equal to 0.5, but an analysis of the dependence of the results on this value is provided in Supplementary Fig. 1.
The optimization algorithm converged within 150 iterations and the first and second wave-modelling resulting values for the optimized parameters are reported in Table 4 .
Table 4.
Parameters for the A-SIR model obtained through the fit of I(t) for the first wave and the second wave.
| Estimated Parameters | First wave | Second wave |
|---|---|---|
| 1 | 0.34 | |
| 0.53 | 0.10 | |
| η | 0.88 | 0.29 |
| ξ |
0.10 |
0.14 |
| 1.87 | 3.31 |
We observed that the estimate of asymptomatic recovery rate described by η parameter (estimated to be 0.88 for the first wave and 0.29 for the second wave) was always higher than the symptomatic rate described by parameter (estimated to be 0.53 for the first wave and 0.10 for the second wave). It means that the time of symptomatic recovery was higher than the time of asymptomatic recovery η−1. This finding is consistent with the observation that, even if the symptomatic infection is promptly recognized and swiftly treated, symptomatic patients took longer to discharge than asymptomatic ones [47]. Meanwhile, we found that the optimal estimate for the ratio of clearly symptomatic versus total infections was = 1/10 for the first wave and ξ = 1/7 for the second wave, which is in a good agreement with what has been observed so far [19,31,[42], [43], [44], [45]]. ξIn particular, some studies showed that after 6 months of the outbreak the R0 value oscillated between 1.3 and 7.7, a range wider than other recent pandemic and it reached 13.3 in nosocomial structures [25]. Meanwhile, other studies reported that the R0 value oscillated from 0.5 to 2.5 within the time window from March to May 2020 in Italy and was predicted to be equal to 1.98 in October 2020 in Italy [26]. In the next section, we will present a novel methodology we implemented to estimate R0 that shows how its value oscillates between 0.5 and 8 in Italy in the time frame from the 27th of February 2020 to the 28th of February 2021.
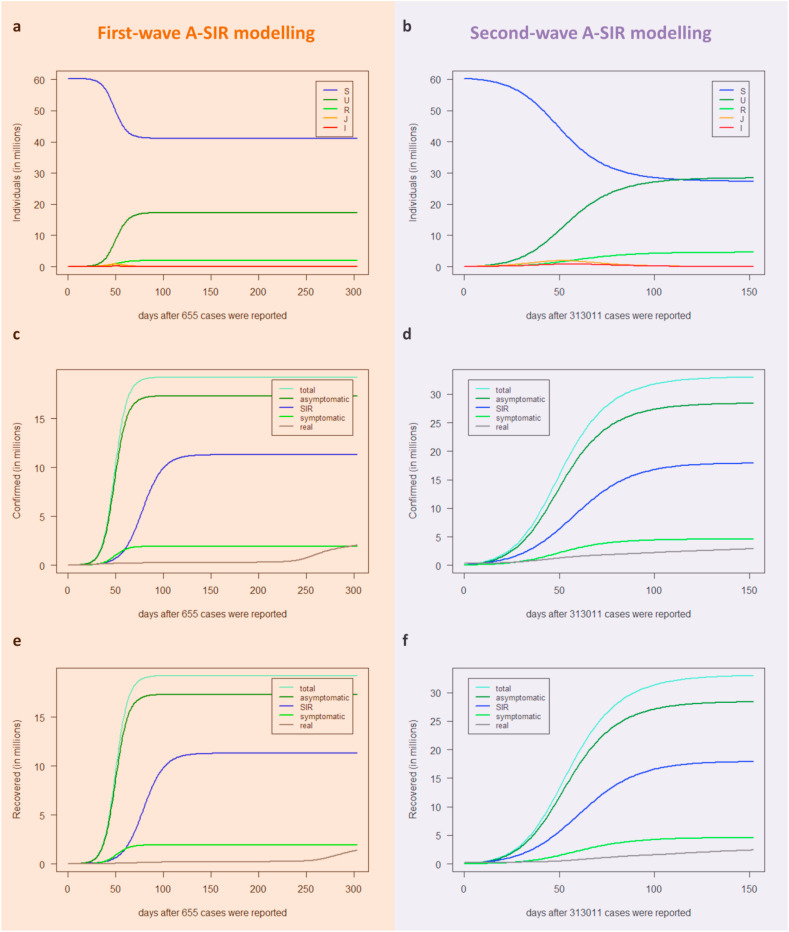
By using the optimal estimated parameters (Table 4), we run the A-SIR model to simulate the behaviour of the epidemic dynamics in Italy during the first and second wave of infection for 304 days and for 153 days starting from time zero, respectively.
The first and second-wave modelling results of the A-SIR model as a function of the number of days after the day corresponding to point zero (t0) are shown (Fig. 5 ). In simulating the first epidemic wave (Fig. 5a), we observed that the height of the epidemic peak of the symptomatic infectives (red curve) was lower than the one predicted by the SIR model (blue curve), and mostly it occurred at an earlier time. Yet, the symptomatic infected curve quite resembled the wavy behaviour of the actual infectives curve (grey curve). Then, the A-SIR model estimated that 10% of the total infectives (yellow curve) were symptomatic (red curve). These findings confirmed the already established observation that the registered infectives, those known to the national health systems and thus isolated and monitored, were only a part of the total pool of infectives and appeared in accordance with the results of [31]. By considering the infectives class as the contribution of symptomatic and asymptomatic people (yellow curve), the A-SIR model overcame the SIR model in simulation of the first wave of infection, since it better estimates the timing of the epidemic peak. On the other hand, these discrepancies are reduced in simulating the second infection wave, where we found that the curve predicted by the A-SIR model for the symptomatic infectives (red curve) nearly coincided with the one predicted by the SIR model (blue curve) and the timing of the epidemic peak is well-estimated by both of them (Fig. 5b). As abovementioned, during this second wave of the infection, the number of infective people registered by the Italian healthcare system already included detected asymptomatic infectives (tested due to contacts with known infectives) and thus also the simpler SIR model was able to provide more reliable predictions.
Fig. 5.
Predictions for the infectives provided by the A-SIR model for the first (a) and second wave (b) in Italy. The total number of infected individuals I + J (yellow lines), symptomatic infected I (red lines), and asymptomatic infected J (orange lines) predicted by the A-SIR model are plotted as a function of days, together with the infected individuals predicted by the SIR model (blue lines) and the real observed infected people in Italy (grey lines). The dark blue points represent real data used to estimate the optimal parameters for the best fitting, i.e. the cumulative number of individuals reported to be infected in Italy up to the 30th of April 2020 after the day that 655 cases were reported (27th of February 2020) for the first peak (a) and from the 29th of September 2020 up to the 30th of November 2020 for the second peak (b).
The epidemic dynamics of the three classes of individuals predicted by the A-SIR model for both the first and the second wave of SARS-CoV-2 infection are shown, together with the comparison with the predictions obtained by the standard SIR model (Fig. 6 ). Both SIR and A-SIR models overestimate the confirmed cases compared to the real data, or, equivalently, underestimate the number of susceptible individuals (Fig. 6a–d). In the A-SIR model the overestimation is even more marked but if, consistently with the model itself, we compare the real confirmed cases to the modelled symptomatic cases (I(t)+R(t)) the overestimation is significantly reduced and becomes less than the SIR counterpart. Similar conclusions can be drawn from the comparison between the removed cases (Fig. 6e–f). In fact, if we only include the symptomatic removed cases for the A-SIR evaluation, the difference between real and modelled data is much less than that obtained with the SIR model.
Fig. 6.
Predictions for the three classes provided by the A-SIR model during the first wave (a-c-e) and the second wave (b-d-f) in Italy. The model simulates the long-term behaviour of the epidemic dynamics in Italy, i.e. 304 days after the 27th of February 2020 (a-c-e) and 153 days after the 29th of September 2020 (b-d-f) when the epidemic broke out in Italy for the first and second wave infection, respectively. (a–b) Blue lines represent susceptible S(t); dark green lines represent the asymptomatic recovered U(t); green lines represent the symptomatic recovered R(t); orange lines represent asymptomatic infectives J(t); red lines represent symptomatic infectives I(t). (c–d) Water blue lines represent the total number of confirmed I(t) + J(t) + R(t) + U(t) (i.e., symptomatic and asymptomatic) predicted by the A-SIR model; dark green lines represent the asymptomatic confirmed J(t) + U(t) predicted by the A-SIR model; blue lines represent the confirmed cases predicted by the SIR model; green lines represent the symptomatic confirmed I(t)+R(t) predicted by the A-SIR model; and grey lines correspond to the actual registered confirmed cases in Italy. (e–f): Water blue lines represent the total number of recovered R(t) + U(t) (i.e., symptomatic and asymptomatic) predicted by the A-SIR model; dark green lines represent the asymptomatic recovered U(t) predicted by the A-SIR model; blue lines represent the recovered individuals predicted by the SIR model; green lines represent the symptomatic recovered R(t) predicted by the A-SIR model; and grey lines correspond to the actual registered recovered people in Italy.
Eventually, we applied both the standard SIR and A-SIR model to study the COVID-19 epidemic dynamic in other countries (i.e. Spain, Germany, and France), which we selected as, similarly to Italy, they faced a long phase of lockdown with severe restrictions in social contacts and mobility, managing to drastically reduce the number of daily COVID-19 infections, and released almost simultaneously lockdown measures. In particular, for both the first and second wave modelling of those countries, we chose time windows of comparable lenghts and whose start dates showed a comparable number of confirmed cases with respect to Italy. The scenarios of COVID-19 infections in those countries predicted by SIR and A-SIR models are reported in Supplementary File 1. Our finding confirmed what we have already observed for Italy, that is the SIR model failed to properly reproduce data in the presence of undetected asymptomatic infectives (first peak of infection), overestimating certain very relevant parameters and underestimating others; whereas the SIR model well-fitted in most cases with the wavy behaviour characterizing the infected population curve when detected asymptomatic infectives were part of the total pool of infectives (second peak of infection).
2.2. Basic reproduction number estimation
In the previous sections, we discussed the ability of SIR models to reproduce the data of the two Italian waves of pandemic infections. We showed that the inclusion of asymptomatic infected in the A-SIR model allows to reduce the modelling error especially in the first wave in which, as known, the quality of the measured data is considerably limited by the scarcity of performed swabs. However, the trends of the different populations – infected, susceptible and removed – still show significant discrepancies between models and measured data, and, in particular, a single set of modelling parameters is not able to reproduce the trends of more than one wave thus making the use of the model itself very limited as a predictive tool. Among the intrinsic limitations of the adopted SIR models, the assumption of constant contagion parameters over time appears critical to reproduce time-dependent factors affecting the pandemic evolution, e.g., the imposition and relaxation of confinement measures. In this section, we focus on the temporal variability of the measured data, estimating the basic reproduction number R0 not as a fixed characteristic of a certain wave – as occurs in the considered SIR models – but as a continuous function of time throughout the time range of the pandemic. Different estimation methods of the R0 are available and the optimal choice is still a debated topic [48]. In the present work, we propose and discuss a simple but robust method of evaluating R0. The estimation strategy follows a similar reasoning to that used to derive the Lotka-Euler equation [49,50]. In particular, let be as the transmissibility of a random infected individual at infection age a (time after the infection). This quantity can be interpreted as the product between the probability that the subject is infected at time a and the transmission rate always at the same time. The entire population is assumed to be susceptible to infection, a reasonable hypothesis considering an epidemic phase in which a large majority of individuals have not contracted the virus. The reproduction number can therefore be evaluated as:
We also assume that the population has a uniform rate of contact. Let be the incidence rate of infections, i.e. is the number of new infections in the interval . New infections can be expressed as the sum of all infections caused by infected individuals at time , weighted by the transmissibility of such individuals at infection age a.
Assuming an exponential trend for , it is possible to develop the previous equations and obtain an expression for which involves the exponential growth rate and the moment generating function of normalized transmissibility (serial interval distribution) [47]. More simply, an estimate of can be obtained from the previous formulas assuming that the transmissibility of an individual is constant during an infection age interval between and . These values can be considered reasonably uniform during the evolution of the epidemic and can therefore be extracted from sample studies during the epidemic itself (e.g., contact tracing investigations). Under these assumptions, the previous formulas are simplified as:
from which it is found that:
The function can therefore be evaluated as the ratio between new infections at time t and the mean of new infections between time and time (. In conclusion, it is possible to roughly estimate the trend of starting from the data of the new infections by setting the start and end times of contagiousness. In the following, we chose to estimate by selecting different values of and to have a comparative evaluation of the range of obtainable values. In particular, measuring infection ages as number of days, , and have been evaluated, that are i) the new infections at time t over the mean of infections occurred during the previous 7 days, ii) the new infections at time t over the mean of infections occurred during the previous 25 days, iii) the new infections at time t over the mean of the infections occurred from 18 to 4 days before. The last choice is the most theoretically consistent, as it includes a start infection age greater than zero, thus allowing to eliminate the possibility that a contagion was caused by an immediately previous contagion. It is worth noting that this possibility of including a non-infectious incubation period is absent in the SIR modelling. To mitigate the fluctuations due to measurements of non-uniform data within the week, the smoothed versions – within the weekly window – of the estimates of in the three above-mentioned scenarios in Italy were calculated and shown (Fig. 7 ).
Fig. 7.
Estimation of the basic reproduction numberin Italy. The smoothed versions of the estimates of as a function of time t (days) are plotted for the three contagiousness scenarios: (a), (b), and (c). We assumed as t = 0 the 22nd of January 2020, typical assessment of the start date of the pandemic outbreak in Wuhan. The orange and violet rectangles highlight the time frames we used to simulate, within the SIR and A-SIR frameworks, the first (i.e., from 27th of February 2020 up to 27th of September 2020) and second wave (i.e., from 29th of September 2020 up to 28th of February 2021) in Italy. For each time frame, the maximum and the minimum value of the estimated were highlighted.
In the time frame we used to simulate, within the SIR and A-SIR frameworks, the first wave of infection in Italy (from 27th of February 2020 up to 27th of September 2020), we observe that the estimates of highly fluctuated around 1, reaching values much greater than 1 within the first 30 days when the pandemic prompted a spike of outbreaks in Italy (with a peak varying from 2 to 8), and showing a growing amplitude of fluctuations in the three scenarios: from the estimates of with values varying in the range of 0.8–2.3 (Fig. 7a), to those ones of in the range of 0.48–7.2 (Fig. 7b), up to those ones of in the range of 0.53–8.2 (Fig. 7c). Even though such a discontinuous trend certainly represents a sudden explosion of infections, it is also likely to be attributed to the reduced quality of the data due to the limited use of swabs in the initial phase.
On the other hand, in the time frame we used to simulate the second wave of infection in Italy (from the 29th of September 2020 to 28th of February 2021), we observe a quite steady trend of the estimates, with less broad fluctuations around 1, whose amplitude slightly grows in the three scenarios leading to more coherent estimations among each other, especially for the second and third scenarios: from with values varying in the range of 0.87–1.38 (Fig. 7a), to in the range of 0.67–2.5 (Fig. 7b), and up to in the range of 0.69–2.6 (Fig. 7c).
All in all, the trends of over time shows a more complex dynamic than the rigid categorization in waves, with a continuously fluctuating trend that is also driven by time-dependent external factors – such as confinement rules – and possibly by the evolution of the virus itself in its most recent variants. The reproduction of such an evolution using predictive models is still challenging. The estimates of for other selected countries (i.e. Spain, Germany, and France) compaired with the ones obtained for Italy are reported in Supplementary File 1, showing mostly comparable trends.
3. Discussion
The occurrence of subsequent waves of COVID-19 cases represents a unique pattern orchestrated by SARS-CoV-2 virus, which was not observed in the other coronaviruses, such as SARS-CoV and MERS-CoV. In fact, unlike the latter showing a controlled and very low human-to-human transmission and therefore were characterized by contained outbreaks in more limited geographic areas, SARS-CoV-2 has an uncontrolled and high human-to-human transmission: even vaccinated people become infected and can transmit the virus, as well as asymptomatic unvaccinated people. This could likely lead to an endemic virus that may never go away. Therefore, having models for simulating how the virus will circulate is of fundamental importance for setting up adequate control strategies and prevention measures.
However, the quality of the data is not always adequate to face the complexity of many computational models and hampers a fair calibration of the parameters and the evaluation of their relative performance. A bear witness of poor data reliability is the clear difference of detection of the large cohort of asymptomatic infectives during the two infection waves. In the early epidemic phase, swabs were made only to patients with severe symptoms taken to hospital or intensive care unit, since the priorities of every national health system, heavily struck by COVID-19, were to deal with the emergency. As consequence, asymptomatic people, not seeking medical assistance and hence hidden to the national health system, remained undetected. On the contrary, during the second wave of infection, a percentage of asymptomatic infectives was included in the total ammount of infected people, since they were tested due to close contacts with swab positives and thus being detected by the health system.
To address this issue, in the present study we started from the simplest standard SIR model and then we compared its outcomes with the ones resulting from the more sophisticated A-SIR model proposed in Ref. [31], which explicitly takes into account the presence of a large set of asymptomatic infectives as further fuel to the spread of infection.
Our goal was to assess the performance of both models in predicting the first and second wave of infection in different countries that simultaneously faced a long phase of lockdown - including Italy, Spain, Germany, and France - with data reflecting the enforcing/relaxing of confinement measures. Yet, we aimed to verify whether the conclusions drawn up by the authors of [31] while simulating the first wave of COVID-19 infection, continued to hold even when the quality of the data is higher as the case of the second wave.
Thus, we firstly applied both the SIR and the A-SIR model to the COVID-19 epidemic in Italy and we solved them via numerical simulations for realistic values of the parameters obtained by calibrating the model with the same epidemiological data available for a time frame of two months before the flattening of the first (March–April 2020) and second infection peak (October–November 2020). Then, we simulated the COVID-19 epidemics dynamics also in Spain, Germany, and France starting from the same initial configuration of the model parameters as in Italy.
As expected, we found that the predictions extracted for the infectives outside the period used to fix the model parameters, but still remaining far from the second wave peaking period, grossly differed if these were analyzed using the SIR or the A-SIR models, with the A-SIR model resulting much better in predicting the evolution of the first wave of infection. In fact, in the presence of a large number of undetected asymptomatic infectives the standard SIR model leads to overestimating certain very relevant parameters and underestimate others. These findings confirmed the results of [31], when applied in an analogous time frame nearby the first wave peaking period, and point out the unquestionable and absolute necessity of considering the presence of undetected asymptomatic individuals to obtain more realistic outcomes.
The situation drastically changed, when we dealt with more accurate data to calibrate the model that considered detected asymptomatic infectives, being tested due to close contacts with swab positives and thus registered by the health system. Since they do not think to be sick and therefore do not self-isolate, asymptomatic people come into contact with more people than symptomatic individuals posing a serious threat to public health and leading to an increase of the actual value of R0 (Table 4, First wave column). Thus, differently from what was predicted by our previous analysis and by the one in Ref. [31] for the first wave modelling, we found that the outcomes of both the models nearly coincided and well-fit with the shape of the actual epidemic curve of infected during the time span nearby the occurrence of the second peak of the infection (Fig. 5d).
4. Conclusions
In this study, we demonstrated that with the same set of model parameters it is not possible to simulate different trends of a relevant epidemic when available data used to calibrate the model strongly depends on the situations at hand and don't show any periodicity that could aid the model training process. The first and the second wave of SAR-Cov-2 infection were completely different from each other and the SIR-type models we implemented here have to use different values for the equation parameters to obtain the best fit of the data. Our findings thus indicate that increasing the complexity of the model is useless and unnecessarily wasteful if not supported by an increased quality of the available data. Of course, more detailed models can surely be cast, but the very simple SIR model is sufficient to explain the infection dynamics when the quality of the real data is fairly good to provide a well model fitting, but not high enough to justify additional parameters, which can barely be inferred by the available data. Certainly, the usage of more complex models is mandatory when interested in understanding how the infection dynamics depends on specific variables, like the deploying different non-pharmaceutical interventions by governments around the world [51], the enforcing/relaxing ‘stay-at-home’ restrictions [33,34], the level of casual contacts [34], the number of patients taken to hospitals or to intensive care units [34], the percentage of patients with a weak immunity system [35] and so forth [32].
4.1. Limitations of the study and future directions
The main limitation of the SIR-types models implemented in this study relies in their deterministic nature that disregards typical evolution parameters of the COVID-19 dynamics, including the containment measurements adopted by the governments across the world and the rapid spread of the new virus variants. As future direction, we intend to develop a more complex model that will explicitly consider these parameters in order to highlight how the reactivity of certain measures plays a fundamental role in limiting the spread of the infection and therefore the overall number of deaths, the most important factor for evaluating the success of an epidemic management. In fact, the evaluation of the impact of the various containment measures potentially allows to re-calibrate the adopted strategies through the evaluation of faster and more precise strategies, thus limiting the dramatic sanitary consequences and, at the same time, not compromising the economic and social stability of the country.
However, developing models capable of replicating past epidemiological trends of the ongoing COVID-19 pandemic – or even more ambitiously able to predict future trends – is extremely challenging, given the poor quality of the available data and the lack of recurrent pattern. In order to overcome this limitation, we will use the Italian past context as case study. In fact, in order to control the SARS-CoV-2 epidemic, the Italian government adopted a national tiered system that divided Italian regions into red, orange, yellow and white zones depending on how severe the coronavirus situation was locally. Since this tiered framework has been uniformly applied on a national scale, it led to high-quality data available at a regional level, which in turn can be analyzed in parallel to increase the reliability of the parameters estimation.
5. Methods
5.1. Data accessibility
The time-series data for the coronavirus disease (COVID-19) were obtained from the COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University available at https://github.com/CSSEGISandData/COVID-19. In particular, we downloaded the available time series tables for the global confirmed cases, recovered cases, and deaths and we extracted data of countries here investigated (i.e. Italy, Spain, Germany, and France).
5.2. The SIR model
The SIR model was implemented in R (version 3.6.1) and tested on the following operating systems: macOS High Sierra 10.13.6 and Windows 10 Pro version 20H2 (OS builds 19042.867). The equations describing the model are defined in the corresponding subsection of the Results and Discussion section. The input parameters that determine the probabilities of events occurring are: β describing the contact rate, and γ describing the removal rate. The SIR model was solved via numerical simulations by using ode function of deSolve R package. It takes as input the optimal values of β and γ parameters obtained by using the optim function of stats R package. We chose the algorithm called “L-BFGS-B” as the method for the optim function, referring to the algorithm developed in Ref. [41]. For the fitting, we used time-series data of the two months preceding the flattening of the first and second peak in Italy, from the 27th of February 2020 to the 30th of April 2020 and from the 29th of September 2020 to the 30th of November 2020, respectively. The initial model configuration and the first and second wave-modelling resulting parameters are given in Table 1, Table 2, respectively. Details about the fitting process, the initial configuration and the first and second wave-modelling resulting parameters when simulation the COVID-19 epidemic dynamics in Spain, Germany, and France, are provided in Supplementary File 1.
5.3. The A-SIR model
The A-SIR model was implemented in R (version 3.6.1) and tested on the following operating systems: macOS High Sierra 10.13.6 and Windows 10 Pro version 20H2 (OS builds 19042.867). The equations describing the model are defined in the corresponding subsection of the Results and Discussion section. The input parameters that determine the probabilities of events occurring are: β describing the contact rate; and describing the recovery rate at which symptomatic and asymptomatic people are removed from the epidemic dynamics, respectively; and ξ describing the fraction of symptomatic individuals over the total of infectives. The A-SIR model was solved via numerical simulations by using ode function of deSolve R package. It takes as input the optimal values of the parameters obtained by using the optim function of stats R package. We chose the algorithm called “L-BFGS-B” as the method for the optim function, referring to the algorithm developed in Ref. [41]. For the fitting, we used time-series data of the two months preceding the flattening of the first and second peak in Italy, from the 27th of February 2020 to the 30th of April 2020 and from the 29th of September 2020 to the 30th of November 2020, respectively. The initial model configuration and the first and second wave-modelling resulting parameters are given in Table 3, Table 4, respectively. Details about the fitting process, the initial configuration and the first and second wave-modelling resulting parameters when simulation the COVID-19 epidemic dynamics in Spain, Germany, and France, are provided in Supplementary File 1.
5.4. R-code availability
All data generated during this study are included in this published article. The R-code of the SIR model and the A-SIR model is open-source and freely available at https://github.com/sportingCode/COVID-19_dynamicsSimulation.git.
Author contributions
Conceptualization: PP and ARG; Supervision and Project administration: PP; Methodology: PP and GF; Software: PP and GF implemented SIR and A-SIR models in R-code; FS developed the new methodology to evaluate the basic reproduction number R0; VG implemented a deep learning approach in Python; Formal analysis: all the authors; Writing – original draft: all the authors; Writing – review & editing: all the authors.
Acknowledgements
This work was financially supported by PRIN 2017 - Settore ERC LS2 - Codice Progetto 20178L3P38.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.compbiomed.2021.104657.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.Lefkowitz E.J., Dempsey D.M., Hendrickson R.C., et al. Virus taxonomy: the database of the international committee on taxonomy of viruses (ICTV) Nucleic Acids Res. 2018;46:D708–D717. doi: 10.1093/nar/gkx932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhu N., Zhang D., Wang W., et al. A novel coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 2020;382:727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Woo P.C.Y., Lau S.K.P., Huang Y., et al. Coronavirus diversity, phylogeny and interspecies jumping. Exp Biol Med Maywood NJ. 2009;234:1117–1127. doi: 10.3181/0903-MR-94. [DOI] [PubMed] [Google Scholar]
- 4.Woo P.C., Lau S.K., Yuen K. Infectious diseases emerging from Chinese wet-markets: zoonotic origins of severe respiratory viral infections. Curr. Opin. Infect. Dis. 2006;19:401–407. doi: 10.1097/01.qco.0000244043.08264.fc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Woo P.C.Y., Lau S.K.P., Lam C.S.F., et al. Discovery of seven novel Mammalian and avian coronaviruses in the genus deltacoronavirus supports bat coronaviruses as the gene source of alphacoronavirus and betacoronavirus and avian coronaviruses as the gene source of gammacoronavirus and deltacoronavirus. J. Virol. 2012;86:3995–4008. doi: 10.1128/JVI.06540-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cui J., Li F., Shi Z.-L. Origin and evolution of pathogenic coronaviruses. Nat. Rev. Microbiol. 2019;17:181–192. doi: 10.1038/s41579-018-0118-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chan J.F.-W., Kok K.-H., Zhu Z., et al. Genomic characterization of the 2019 novel human-pathogenic coronavirus isolated from a patient with atypical pneumonia after visiting Wuhan. Emerg. Microb. Infect. 2020;9:221–236. doi: 10.1080/22221751.2020.1719902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lu R., Zhao X., Li J., et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding. Lancet. 2020;395:565–574. doi: 10.1016/S0140-6736(20)30251-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schoeman D., Fielding B.C. Coronavirus envelope protein: current knowledge. Virol. J. 2019;16:69. doi: 10.1186/s12985-019-1182-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sikkema R.S., Farag E.a., Ba, Islam M., et al. Global status of Middle East respiratory syndrome coronavirus in dromedary camels: a systematic review. Epidemiol. Infect. 2019;147:e84. doi: 10.1017/S095026881800345X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weekly epidemiological update - 29 December 2020. https://www.who.int/publications/m/item/weekly-epidemiological-update---29-december-2020
- 12.Zheng J. SARS-CoV-2: an emerging coronavirus that causes a global threat. Int. J. Biol. Sci. 2020;16:1678–1685. doi: 10.7150/ijbs.45053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wrapp D., Wang N., Corbett K.S., et al. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science. 2020;367:1260–1263. doi: 10.1126/science.abb2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wadman M., Couzin-Frankel J., Kaiser J., et al. A rampage through the body. Science. 2020;368:356–360. doi: 10.1126/science.368.6489.356. [DOI] [PubMed] [Google Scholar]
- 15.Huang C., Wang Y., Li X., et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet Lond Engl. 2020;395:497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pan F., Ye T., Sun P., et al. Time course of lung changes at chest CT during recovery from coronavirus disease 2019 (COVID-19) Radiology. 2020;295:715–721. doi: 10.1148/radiol.2020200370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bai Y., Yao L., Wei T., et al. Presumed asymptomatic carrier transmission of COVID-19. J. Am. Med. Assoc. 2020;323:1406–1407. doi: 10.1001/jama.2020.2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kimball A., Hatfield K.M., Arons M., et al. Asymptomatic and presymptomatic SARS-CoV-2 infections in residents of a long-term care skilled nursing facility - king county, Washington, March 2020. MMWR Morb. Mortal. Wkly. Rep. 2020;69:377–381. doi: 10.15585/mmwr.mm6913e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li R., Pei S., Chen B., et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368:489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qiu J. Covert coronavirus infections could be seeding new outbreaks. Nature. Epub ahead of print 20 March 2020. DOI: 10.1038/d41586-020-00822-x. [DOI] [PubMed]
- 21.Zou L., Ruan F., Huang M., et al. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N. Engl. J. Med. 2020;382:1177–1179. doi: 10.1056/NEJMc2001737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tan J, Liu S, Zhuang L, et al. Transmission and clinical characteristics of asymptomatic patients with SARS-CoV-2 infection. Future Virol.. DOI: 10.2217/fvl-2020-0087.
- 23.Baggett T.P., Keyes H., Sporn N., et al. Prevalence of SARS-CoV-2 infection in residents of a large homeless shelter in Boston. J. Am. Med. Assoc. 2020;323:2191–2192. doi: 10.1001/jama.2020.6887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Arevalo-Rodriguez I., Buitrago-Garcia D., Simancas-Racines D., et al. False-negative results of initial RT-PCR assays for COVID-19: a systematic review. PloS One. 2020;15 doi: 10.1371/journal.pone.0242958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Temime L., Gustin M.-P., Duval A., et al. A conceptual discussion about the basic reproduction number of severe acute respiratory syndrome coronavirus 2 in healthcare settings. Clin Infect Dis Off Publ Infect Dis Soc Am. 2021;72:141–143. doi: 10.1093/cid/ciaa682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fernández-Villaverde J, Jones CI. Estimating and simulating a SIRD model of COVID-19 for many countries, states, and cities. Natl Bur Econ Res. Epub ahead of print 11 May 2020. DOI: 10.3386/w27128. [DOI] [PMC free article] [PubMed]
- 27.Chen J. Pathogenicity and transmissibility of 2019-nCoV-A quick overview and comparison with other emerging viruses. Microb. Infect. 2020;22:69–71. doi: 10.1016/j.micinf.2020.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kermack W.O., McKendrick A.G., Walker G.T. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. - Ser. A Contain. Pap. a Math. Phys. Character. 1927;115:700–721. [Google Scholar]
- 29.Anastassopoulou C., Russo L., Tsakris A., et al. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PloS One. 2020;15 doi: 10.1371/journal.pone.0230405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos, Solit. Fractals. 2020;134:109761. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gaeta G., Gaeta G. A simple SIR model with a large set of asymptomatic infectives. Math Eng. 2021;3:1–39. [Google Scholar]
- 32.Peirlinck M., Linka K., Sahli Costabal F., et al. Visualizing the invisible: the effect of asymptomatic transmission on the outbreak dynamics of COVID-19. Comput. Methods Appl. Mech. Eng. 2020;372:113410. doi: 10.1016/j.cma.2020.113410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Faranda D., Alberti T. Modeling the second wave of COVID-19 infections in France and Italy via a stochastic SEIR model. Chaos Interdiscip J Nonlinear Sci. 2020;30:111101. doi: 10.1063/5.0015943. [DOI] [PubMed] [Google Scholar]
- 34.Renardy M., Eisenberg M., Kirschner D. Predicting the second wave of COVID-19 in Washtenaw county, MI. J. Theor. Biol. 2020;507:110461. doi: 10.1016/j.jtbi.2020.110461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ghanbari B. On forecasting the spread of the COVID-19 in Iran: the second wave. Chaos, Solit. Fractals. 2020;140:110176. doi: 10.1016/j.chaos.2020.110176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fokas A.S., Dikaios N., Kastis G.A. Mathematical models and deep learning for predicting the number of individuals reported to be infected with SARS-CoV-2. J. R. Soc. Interface. 2020;17:20200494. doi: 10.1098/rsif.2020.0494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Diekmann O., Heesterbeek J.A.P., Metz J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- 38.Heesterbeek J.A.P. A brief history of R0 and a recipe for its calculation. Acta Biotheor. 2002;50:189–204. doi: 10.1023/a:1016599411804. [DOI] [PubMed] [Google Scholar]
- 39.Sanyaolu A., Okorie C., Marinkovic A., et al. Comorbidity and its impact on patients with COVID-19. Sn Compr Clin Med. 2020:1–8. doi: 10.1007/s42399-020-00363-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.The Italian National Istitute of Statistics www.istat.itwww.istat.it
- 41.Byrd R.H., Lu P., Nocedal J., et al. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995;16:1190–1208. [Google Scholar]
- 42.Lavezzo E., Franchin E., Ciavarella C., et al. Suppression of a SARS-CoV-2 outbreak in the Italian municipality of Vo’. Nature. 2020;584:425–429. doi: 10.1038/s41586-020-2488-1. [DOI] [PubMed] [Google Scholar]
- 43.Lourenço J., Paton R., Thompson C., et al. Fundamental principles of epidemic spread highlight the immediate need for large-scale serological surveys to assess the stage of the SARS-CoV-2 epidemic. medRxiv. 2020:2020. [Google Scholar]
- 44.Flaxman S., Mishra S., Gandy A., et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020;584:257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- 45.http://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/
- 46.https://www.theguardian.com/world/2020/mar/12/uk-governments-coronavirus-advice-and-why-it-gave-it
- 47.Lee Y-H, Hong CM, Kim DH, et al. Clinical course of asymptomatic and mildly symptomatic patients with coronavirus disease admitted to community treatment centers, South Korea - volume 26, number 10—october 2020 - emerging infectious diseases journal - CDC. DOI: 10.3201/eid2610.201620. [DOI] [PMC free article] [PubMed]
- 48.Cori A., Ferguson N.M., Fraser C., et al. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013;178:1505–1512. doi: 10.1093/aje/kwt133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wallinga J., Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc R Soc B Biol Sci. 2007;274:599–604. doi: 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ma J. Estimating epidemic exponential growth rate and basic reproduction number. Infect Dis Model. 2020;5:129–141. doi: 10.1016/j.idm.2019.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Brauner JM, Mindermann S, Sharma M, et al. Inferring the effectiveness of government interventions against COVID-19. Science; 371. Epub ahead of print 19 February 2021. DOI: 10.1126/science.abd9338. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The time-series data for the coronavirus disease (COVID-19) were obtained from the COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University available at https://github.com/CSSEGISandData/COVID-19. In particular, we downloaded the available time series tables for the global confirmed cases, recovered cases, and deaths and we extracted data of countries here investigated (i.e. Italy, Spain, Germany, and France).