Abstract
The pathophysiology of major depressive disorder (MDD) has been explored to be highly associated with the dysfunctional integration of brain networks. It is therefore imperative to explore neuroimaging biomarkers to aid diagnosis and treatment. In this study, we developed a spatiotemporal graph convolutional network (STGCN) framework to learn discriminative features from functional connectivity for automatic diagnosis and treatment response prediction of MDD. Briefly, dynamic functional networks were first obtained from the resting‐state fMRI with the sliding temporal window method. Secondly, a novel STGCN approach was proposed by introducing the modules of spatial graph attention convolution (SGAC) and temporal fusion. A novel SGAC was proposed to improve the feature learning ability and special anatomy prior guided pooling was developed to enable the feature dimension reduction. A temporal fusion module was proposed to capture the dynamic features of functional connectivity between adjacent sliding windows. Finally, the STGCN proposed approach was utilized to the tasks of diagnosis and antidepressant treatment response prediction for MDD. Performances of the framework were comprehensively examined with large cohorts of clinical data, which demonstrated its effectiveness in classifying MDD patients and predicting the treatment response. The sound performance suggests the potential of the STGCN for the clinical use in diagnosis and treatment prediction.
Keywords: functional connectivity, graph convolutional network, individual diagnosis, major depressive disorder, treatment response prediction
In this study, we developed a spatiotemporal graph convolutional network framework to learn discriminative features from functional connectivity for automatic diagnosis and treatment response prediction of major depressive disorder. Performances of the framework were comprehensively examined with large cohorts of clinical data, which demonstrated its effectiveness in classifying major depressive disorder patients and predicting the treatment response.
1. INTRODUCTION
Major depressive disorder (MDD) is a severe psychiatric disorder characterized by deep sadness, low energy and a high risk of suicide, which is accompanied by substantial mortality (Dwyer et al., 2020, Sekhon, Patel, & Sapra, 2020). During the past decades, various efforts have been made to combat the heightened mortality caused by MDD. Typically, syndrome‐based clinical routines are utilized to aid in its diagnosis as well as inform clinical treatment. However, due to the limited diagnosis accuracies (Stephan et al., 2016), a significant portion of patients fails to respond to the first‐line treatment with antidepressants, and the response can only be determined after about 1 month (Bauer et al., 2015). The treatment resistance not only affects the compliance of antidepressant treatment and but also incurs the risk of developing mental disability for poorly responsive patients. Given the serious prevalence of the MDD and a lack of its effective management, it is highly imperative to explore objective biomarkers for detection and treatment response prediction of MDD.
It has been established that the pathophysiology of MDD is intimately associated with dysfunctional integrations of brain networks (Hou et al., 2018; Kaiser, Andrews‐Hanna, Wager, & Pizzagalli, 2015). As such, brain functional connectivity derived from functional magnetic resonance imaging (fMRI) has been widely used in the recent past to discriminate MDD from healthy controls and to predict treatment response for MDD as well. Indeed, many endeavors have been made with the intent to explore potential biomarkers for MDD diagnosis on the basis of functional connectomes (Bhaumik et al., 2017; Rosa et al., 2015; Zhao et al., 2020). Most of these studies resorted to multivariate pattern analysis of functional connectivity measures derived among brain regions. While promising in offering novel neuroimaging biomarkers for MDD, these methods, or diagnosis models, typically utilize static features of functional connectivity with topological and dynamic features basically ignored. The topologies and dynamics of functional connectivity have in fact been found to be closely related to the pathophysiology of MDD (Hultman et al., 2018; Ramirez‐Mahaluf, Roxin, Mayberg, & Compte, 2017; Sendi et al., 2021), which thus may provide vital clues to accurate diagnosis of MDD.
Recently, the notion of deep learning has gained considerable popularity in the research realm of computer vision and pattern recognition (Badrinarayanan, Kendall, & Cipolla, 2017; Bao et al., 2020), and deep graph learning has achieved unprecedented success in numerous applications (Chang et al., 2020; Valsesia, Fracastoro, & Magli, 2020). As the brain network can be described as a graph, in which parcellated brain regions are treated as nodes and connectivity metrics between these regions as edges, deep graph learning can be naturally extended to characterizations of intrinsic features of brain functional connectivity (Jiang et al., 2020; Zhang, Kong, Wu, Coatrieux, & Shu, 2019). The power of deep graph learning lies in its capability of learning intrinsic topological features from graph, which allows it to yield performances superior to traditional deep learning approaches. The powerful technique has recently been introduced for diagnosis of brain disorders. Ktena et al. (2018) applied the spectral graph convolutional network with each subject as nodes and functional connectivity as features. The diagnosis was performed by classifying the nodes into different classes with spectral graph convolutional network. Yao et al. (2021) proposed a mutual multi‐scale triplet graph convolutional network to analyze static functional connectivity and structural connectivity for brain disorder diagnosis. Notwithstanding the greatly successful application widely reported in nascent literature, the ability of deep graph learning in individualized diagnosis and treatment response prediction of MDD remains to be explored.
In this study, we developed a spatiotemporal graph convolutional network (STGCN) framework to learn discriminative features from functional connectivity measures for automatic diagnosis and treatment response prediction of MDD. Briefly, dynamic functional networks were first obtained from resting‐state fMRI data with the sliding temporal window method. Secondly, a novel STGCN approach was proposed by introducing modules of spatial graph attention convolution (SGAC) and temporal fusion. A novel SGAC was proposed to improve the feature learning ability and special anatomy prior guided pooling was developed to enable the feature dimension reduction. A temporal fusion module was proposed with the SGAC to capture the dynamic features of functional connectivity between adjacent sliding windows. Finally, the proposed framework was utilized for diagnosis and antidepressant treatment response prediction for MDD. Performances of the framework were comprehensively examined with large cohorts of clinical data, which demonstrated its effectiveness in classifying MDD patients and predicting the treatment response. Insights obtained from our experimentation can help redefine the clinical de facto standard for MDD management, and offer the potential of opening fundamentally novel avenues for individualized treatment of depression.
2. MATERIALS AND METHODS
2.1. Participant
This study‐utilized data sets from two sites, including the Affiliated ZhongDa Hospital of Southeast University and the Second Affiliated Hospital of Xinxiang Medical University. The patients were recruited from the hospitals and the healthy controls (HCs) were recruited through community health screening. All the subjects were unequivocally and naturally right‐handed. Written informed consent was obtained from all the participants. All participants completed a semi‐structured clinical interview for DSM‐IV Axis I Disorders (SCID‐I/P), Clinician Version (First, Spitzer, Gibbon, & Williams, 1997) with two senior psychiatrists. All the participants also had an identical assessment protocol, including the review of medical history and demographic inventory. The patients met the following inclusion criteria: (a) they met the MDD in DSM‐IV criteria at the time of enrollment; (b) they were in the first depressive episode and the age of onset was over 18 years old; (c) 24 items Hamilton Depression Rating Scale (HAMD) were > 20; (d) absence of other major psychiatric illnesses, including substance abuse or dependence; (e) absence of primary neurological illnesses, including dementia or stroke; (f) absence of medical illness impairing cognitive function; (g) no history of receiving electroconvulsive therapy; (h) no gross structural abnormalities on T1‐weight images, and no gross white matter changes such as infarction or other vascular lesions T2‐weighted MRI; (i) no psychotic symptoms (e.g., hallucination/bizarre delusions). The MRI scans were obtained before patients having antidepressant treatment.
After removal of poor quality of imaging due to head motion or ghost intensity, this study included 82 MDD patients and 50 controls from the Affiliated ZhongDa Hospital of Southeast University, and 98 MDD patients and 47 controls from the Second Affiliated Hospital of Xinxiang Medical University.
The patients in the Affiliated ZhongDa Hospital of Southeast University completed the HAMD assessment at the zero and second week. According to the reduction of HAMD (Leucht et al., 2013) (HAMDbaseline − HAMDweek‐2)/HAMDbaseline), the MDD patients were classified into nonresponsive depression (NRD, n = 40) (HAMD score reduction ≤50%) and responsive depression (RD, n = 42) (HAMD score reduction >50%). In total, there were 132 samples, consisting of 50 HCs, 42 RDs, and 40 NRDs.
2.2. Image acquisition
The MRI scans were performed at the Affiliated ZhongDa Hospital of Southeast University and the Second Affiliated Hospital of Xinxiang Medical University. The images were obtained from 3.0 Tesla whole‐body scanner (Siemens Medical Systems, Erlangen, Germany) with a 12‐channel head coil. Subjects laid supine with the head snugly fixed with a belt and foam pads to minimize the head motion. All the subjects were instructed to keep eyes closed, relax, and remain awake with no thinking of anything during the scanning. High resolution three‐dimensional T1 weighted images were obtained using magnetization prepared rapid gradient echo sequences with the following parameters: repetition time (TR) = 1900 ms; echo time (TE) = 2.48 ms; flip angle (FA) = 9°; acquisition matrix = 256 × 256; field of view (FOV) = 250 × 250 mm2; thickness = 1.0 mm; gap = 0, 176 slices; in‐plane resolution = 0.97 × 0.97 mm2. An 8 min resting‐state fMRI was acquired with the following parameters: TR = 2000 ms; TE =25 ms; FA = 90°; acquisition matrix = 64 × 64; FOV = 240 × 240 mm2; thickness = 4.0 mm; gap = 0 mm; 36 axial slices; 240 volumes; 3.75 × 3.75 mm2 in‐plane resolution parallel to the anterior–posterior commissure line.
2.3. Data preprocessing
All the rsfMRI data were preprocessed using the Data Processing Assistant for Resting‐State Function (DPARSF 2.3 Advanced Edition) toolkit. For each subject, the first 10 frames were discarded for magnetic saturation. The following steps were performed: (a) slice timing correction; (b) motion correction; (c) co‐registering T1 to functional image; (d) spatial normalization to Montreal Neurological Institute space; (e) spatial smoothing using a 6 mm full‐width at half‐maximum Gaussian kernel; (f) linear detrend; (g) regression of nuisance signals (white matter, cerebrospinal fluid signals, and global signal), and the head‐motion parameters; (h) temporal band‐passing (0.01–0.08 Hz) to minimize low‐frequency drift and filtering the high‐frequency noise.
2.4. Deep dynamic graph learning for diagnosis and treatment response prediction
A novel STGCN was proposed for diagnosis and treatment response prediction for MDD. The main framework is illustrated in Figure 1. To begin with, dynamic functional networks were obtained from the resting‐state fMRI with the sliding temporal window method. Secondly, a novel STGCN framework was proposed by introducing the modules of SGAC and temporal fusion at each stage. A novel SGAC was proposed to improve the feature learning ability and a special anatomy prior guided pooling was developed to enable the feature dimension reduction. A temporal fusion module was proposed to capture the dynamic features of functional connectivity between adjacent sliding windows with the SGAC. The key modules of the framework were SGAC, anatomy prior graph pooling, and temporal fusion, which will be given detailed description in the following. Finally, the proposed framework was utilized for the two tasks of diagnosis and antidepressant treatment response prediction for MDD.
FIGURE 1.
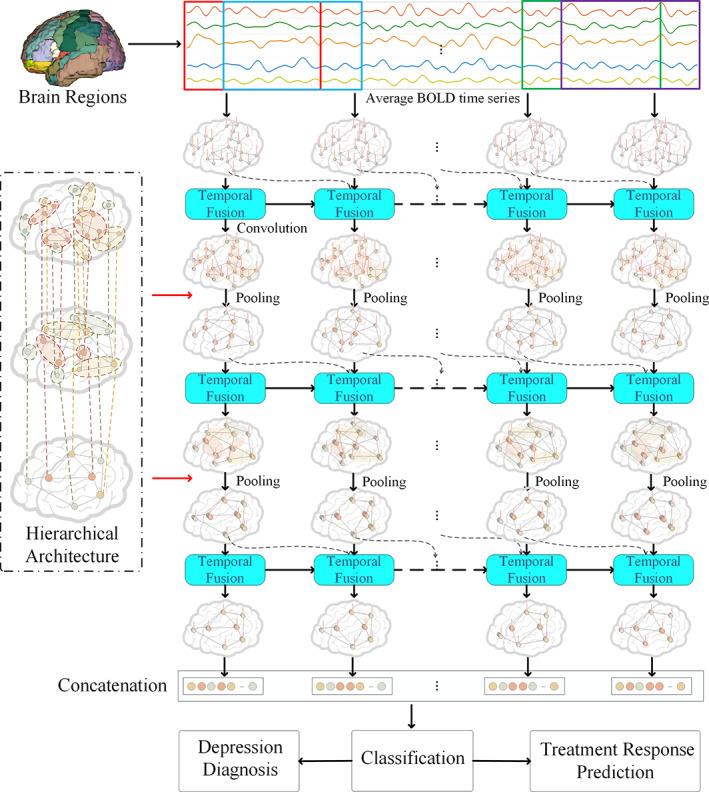
The framework of the proposed spatiotemporal graph convolutional network (STGCN) framework for diagnosis and treatment response prediction of major depressive disorder (MDD). Dynamic functional networks were first obtained from the resting‐state functional magnetic resonance imaging (fMRI) with the sliding temporal window method. Secondly, a novel STGCN framework was proposed by introducing the modules of spatial graph attention convolution (SGAC) and temporal fusion at each stage. A novel SGAC was proposed to improve the feature learning ability. A special anatomy prior graph pooling module was developed to enable the feature dimension reduction with a hierarchical brain parcellation. A temporal fusion module was proposed to capture the dynamic features of functional connectivity between adjacent sliding windows with the spatial graph attention convolution module. Finally, the proposed framework was utilized for the two tasks of diagnosis and antidepressant treatment response prediction for MDD
2.4.1. Construction of the dynamic functional network
Functional connectivity has been demonstrated to be dynamic with temporal variations in recent years (Zalesky, Fornito, Cocchi, Gollo, & Breakspear, 2014; Zhang et al., 2020). Therefore, a set of dynamic functional networks were constructed from resting‐state fMRI data. Firstly, with a selected atlas and the preprocessed data, averaged time courses were computed for each brain region. Secondly, the entire time courses were divided into many overlapping sliding windows, and the Pearson correlation was utilized to calculate the functional connectivity in each sliding window. Several functional connectivities can be obtained with a sliding stride. Finally, the functional connectivity was further thresholded by the proportional quantization to obtain the brain network at each window. The edge number was the same for the functional connectivity at each window (Luo et al., 2021).
These dynamic functional networks can be represented with a set of graphs. The brain regions were the nodes of the graph as V = {V 1, V 2, …, V N }. Each node was represented with the degree and average time courses TS i , i = 1, 2, …, N, where i represents different brain region. The connections between nodes for the kth window were represented as an adjacency matrix A k , where A kij denotes the connection between node i and j at the kth window. Each subject can get K adjacency matrices A = {A 1, A 2, …, A K }, A k ∈ R N × N , and K was number of sliding windows. The feature of a node X ki can be obtained by concatenating the normalized signal feature and the degree of the node D ki is defined with the adjacency matrices as the following
| (1) |
Therefore, a set of dynamic brain networks were obtained with for each sample, and C is the feature dimension of the node.
2.4.2. SGAC
A SGAC module was introduced to learn the features from the graph at each time window. A linear filter is defined to make a combination of the adjacency matrix as following
| (2) |
where I represents the identity matrix, which means the reflexive connection, and h 0, h 1 are the filter coefficients. A k is the adjacency matrix of the graph at the kth sliding window. As each node is represented with the feature of the degree and the average time course, the filter coefficient h 0 or h 1 is a vector with the length C. The size of the output H k is N * N * C. A single feature channel of the linear filter can be described as the following
| (3) |
where represents a slice of H k , which means the corresponding filter of the kth feature h (c) represents the weight corresponding to the cth node feature. The graph convolutional layer can also be utilized to perform on the vertex signal X k as following
| (4) |
where, means the cth column of X k , which represents the cth feature of the vertex, and the parameter b is the bias.
The traditional convolution operation gives the same weights of the neighbor nodes. However, some neighbors are more important than the other ones. Therefore, the attention mechanism is further utilized to identify the effective nodes during the convolution (Petar Velickovic, Casanova, Romero, Lio, & Bengio, 2018). The important neighbor nodes are given larger weights, and while the irrelevant neighbors are suppressed to avoid potentially confusing information. After introducing the attention mechanism, the convolution filter of Equation (4) can be modified as follows,
| (5) |
where att = {att 1 , att 2, …, att N } is the attention weight of each node, which can be learnable with an initial value of 0.
2.4.3. Anatomy prior graph pooling
Graph pooling layer could make the dimension reduction to enable a larger receptive field and a low computational burden. Moreover, the pooling operation can help extracting more distinctive feature information. Commonly utilized graph embedded pooling approach adaptively learns an embedding matrix. This method merges nodes with similar features to generate new nodes. However, the nodes of the graph are the anatomical regions of the brain, and certain neighborhood regions have strong relationships and functional dependencies (Liu et al., 2018). It is better to merge the regions with a similar function. To utilize the prior knowledge, a novel anatomy prior graph pooling method is proposed based on anatomy information between the graph nodes. A hierarchical brain parcellations are utilized at different scales, as shown in Figure 1. The three parcellations of L 1, L 2, and L 3 include 90, 54, and 14 regions of interest. The embedding matrix V emb is obtained by mapping the corresponding brain parcellations with a hierarchical architecture. The 90 nodes with the L 1 level is pooling to 54 nodes at the L 2 level and the 54 nodes at the L 2 level is pooling to 14 nodes at the L 3 level.
With the embedding matrix, a pooled graph can be obtained as follows,
| (6) |
| (7) |
where A in,k and X in,k are the adjacent matrix and feature of the input graph, A out,k and X out,k are the adjacent matrix and feature of the output graph after the pooling operation.
2.4.4. Temporal fusion
MDD has exhibited abnormal temporal dynamics of the functional connectivity (Hou et al., 2018; Hou, Kong, Yin, Zhang, & Yuan, 2021). Therefore, a temporal fusion module is introduced to capture the dynamic feature of functional connectivities among different windows based on the above proposed SGAC module and long short‐term memory. The detailed structure is illustrated in Figure 2. The temporal fusion consists of the forget stage, the select memory stage, and the output stage. The inputs consist of the learned graph feature at current temporal window and the difference between current and previous temporal windows. The SGAC operator is utilized to perform the feature learning.
FIGURE 2.
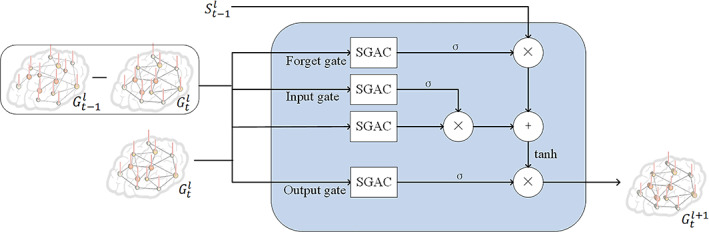
Detailed structure of the temporal fusion module for capturing the dynamic features of the functional connectivity. The temporal fusion consists of the forget stage, the select memory stage, and the output stage. The inputs consist of the learned graph feature at the current temporal window and the difference between current and previous temporal windows. The spatial graph attention convolution (SGAC) operator is utilized to perform the feature learning
The forget stage selectively forgets the stage passed at the last moment, and only keeps the important part. This stage can be calculated with the Equation (8)
| (8) |
where is the output of last window, is the input of this window, g* denotes the SGAC operator in Equation (5) with adjacency and vertex feature as input, and the function Diff calculates the difference between the graph features at temporal window t‐1 and t, which capture the dynamic features of functional connectivity between adjacent temporal windows.
The select memory stage selectively remembers the input of the moment, which includes an input stage and a state vector. The input stage is made up of the sigmoid layer with Equation (9), which determines the values to update.
| (9) |
where g* represents the SGAC operator.
The state vector consists of the tanh layer with Equation (10), which might be entered into the next cell.
| (10) |
The current cell state is thus obtained by multiplying the previous cell state and forget stage, and multiplying the state vector multiplied with input stage, as the Equation (11).
| (11) |
The output stage determines the output of the current moment. A sigmoid layer determines which cell state will be output with Equation (12).
| (12) |
At the same time, the cell state is sent to the tanh layer, and is multiplied by the output of sigmoid gate to obtain the final output with Equation (13).
| (13) |
2.4.5. Optimization and implementation
In the network, the activation function was Rectified Linear Unit (ReLU) and max pooling ϕ(x) = max(0, x) was utilized. The Adam optimization was applied with the learning rate η of 0.01. W represented the parameters to be trained, and the loss function is L(W). Back propagation was utilized for the optimization and the gradient of the loss function g t = ∇ W L(W) was imposed along W.
For Adam optimization, two intermediate variables and their conversions are introduced: m t , v t , , and . The formulas are as follows:
| (14) |
| (15) |
| (16) |
| (17) |
where momentums β is 0.9 in general, m t and v t are the accumulation of all gradients from the beginning of the algorithm to the current step. As all the variables are ready, we can update the parameters with the formula below:
| (18) |
The k‐fold cross‐validation strategy was used to evaluate the performance in the diagnosis and prediction, and the k was set to 10. The k‐fold cross evaluation was performed on each site with the two tasks of diagnosis and prediction. The proposed STGCN method was compared with several methods, including support vector machine (SVM), random forest (RF), deep auto‐encoder (DAE), graph convolutional network (GCN). The performance was quantified using accuracy, sensitivity, and specificity. The k‐fold cross‐evaluation procedure was repeated 10 times to obtain the means and SD of accuracy, sensitivity, and specificity. The two‐sample t test was utilized to compare the classification performance between different methods.
Experiments were performed to evaluate classification performance with the influence of different modules in the proposed STGCN framework. The performance was also quantified using accuracy, sensitivity, and specificity. The k‐fold cross‐evaluation procedure was repeated 10 times to obtain the means and standard deviations of accuracy, sensitivity, and specificity. The two‐sample t test was utilized to compare the classification performance between results varying key modules.
The most discriminating regions were calculated for the diagnosis and treatment response prediction. For each node, the weights were averaged for 10 experiments on the 10‐fold cross‐validation. The top 10 nodes with the largest values were retained as the most discriminating regions for the two tasks of diagnosis and treatment response prediction.
3. RESULTS
3.1. Ten‐fold classification for diagnosis and prediction
The proposed STGCN approach was used for the two tasks of MDD diagnosis and treatment response prediction. The MDD diagnosis was evaluated on the data sets from Zhongda hospital and Xinxiang hospital, and the treatment response prediction was assessed on the data set from the Zhongda hospital. The results of 10‐fold cross‐validation were illustrated as Figure 3. The STGCN achieved accuracies of 84.14 and 83.93%, sensitivities of 89.43%, and 92.93%, specificities of 68.26 and 67.90% on the diagnosis task for the two data sets, respectively. The proposed STGCN obtained significant higher accuracy, sensitivity, specificity than the other four competitive methods for the MDD diagnosis task on both two data sets from Zhongda hospital and Xinxiang hospital (p < .05, two‐sample t test). The proposed STGCN further achieved the performance with accuracy of 89.63%, sensitivity of 84.57%, and specificity of 92.57% for the treatment response prediction on the data set from Zhongda hospital. The accuracy, sensitivity, and specificity are significantly higher than the other four competitive methods for the task of treatment response prediction (p < .05, two‐sample t test).
FIGURE 3.
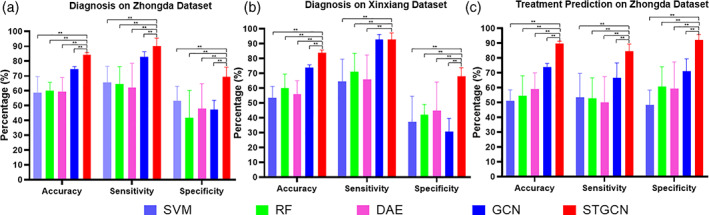
Statistical summary of 10‐fold cross‐validation for MDD diagnosis and treatment prediction. SVM, support vector machine; RF, random forest; DAE, deep auto‐encoder; GCN, graph convolutional network; STGCN, spatiotemporal graph convolutional network. **Denotes the significant differences (p < .05) with two sample t test
3.2. Performance with different modules
The classification performance can be influenced by different modules of the proposed STGCN framework. Experiments were performed with varying the modules of feature, convolution, and pooling, shown in Figure 4. Three kinds of features were validated, including the BOLD signal, node degree, and concatenation of signal and node degree. Concatenation of signal and node degree achieved better performance for the two tasks, shown in Figure 4a. For the convolution module, the proposed SGAC obtained better performance than the traditional edge attention and the result without attention, shown in Figure 4b. As for the pooling module, the proposed anatomy prior graph pooling obtained significantly better performance than the traditional graph embedding pooling, shown in Figure 4c.
FIGURE 4.
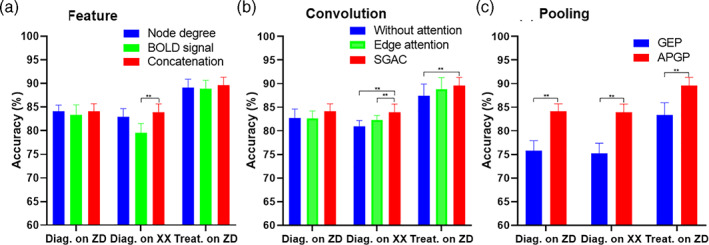
Classification accuracy with different modules for diagnosis on Zhongda hospital and Xinxiang hospital, treatment prediction on Zhongda hospital. (a) Node with different types of features, including node degree (blue), BOLD signal (green), and their concatenation (red). (b) Convolution without attention (blue), with edge attention (green), and with proposed spatial graph attention convolution (SGAC, red). (c) Pooling using graph embedding pooling (GEP, blue) and anatomy prior graph pooling (APGP, red). **Denotes the significant differences (p < .05) with two sample t test
3.3. Performance with key parameters
The proportion of edges and the window length for dynamic functional connectivity generation were two key parameters in the proposed STGCN framework. Experiments were performed to evaluate the performance with varying these two parameters. The performance of accuracy, sensitivity, and specificity were calculated and the results were illustrated in Figure 5 and Figure 6. The proportion of edges was assessed from 0.02 to 0.30 with a step of 0.02. Both the diagnosis and treatment response tasks obtained the best performance at the proportion value of 0.20. The window lengths were evaluated ranging from 60 to 120 with a step of 10. The optimal window length was 100 for both the two tasks.
FIGURE 5.
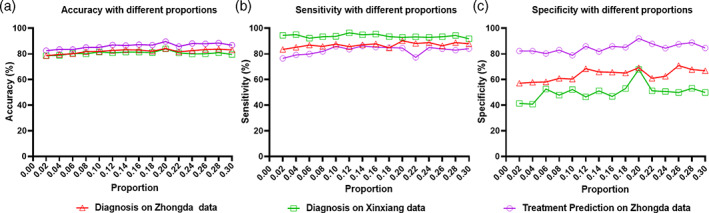
Classification performance of diagnosis on Zhongda hospital (red) and Xixiang hospital (green), treatment prediction (purple) with different proportions of edges. (a) Accuracy (b) Sensitivity, and (c) Specificity
FIGURE 6.
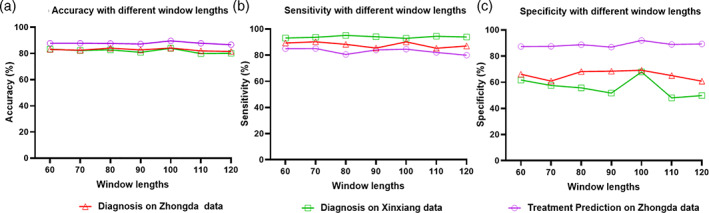
Classification performance of diagnosis on Zhongda hospital (red) and Xixiang hospital (green), treatment prediction (purple) with different lengths of sliding window. (a) Accuracy (b) Sensitivity, and (c) Specificity
3.4. Most discriminative regions
We further analyzed the most discriminating regions for the diagnosis and treatment response prediction, shown in Figure 7. The most discriminating regions for diagnosis regions include the left and right pallidum, right putamen, left and right middle frontal gyrus, right postcentral gyrus, right heschl gyrus, right caudate, right olfactory cortex, right inferior frontal gyrus, and triangular part. The most discriminating regions for treatment response prediction include left and right putamen, right pallidum, left hippocampus, right amygdala, right Caudate, left inferior frontal gyrus, triangular part, left insula, left lingual, and left rectus.
FIGURE 7.
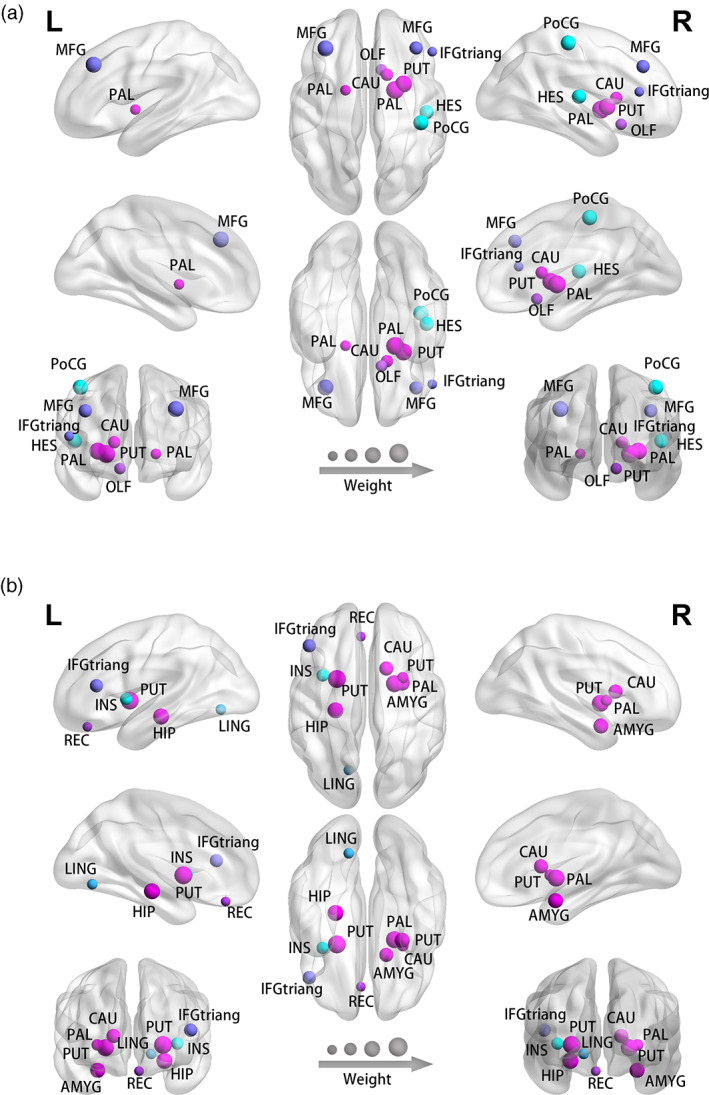
The most discriminative regions of the proposed STGCN approach for (a) diagnosis and (b) treatment response prediction. The most discriminating regions for diagnosis include the left and right pallidum, right putamen, left and right middle frontal gyrus, right postcentral gyrus, right heschl gyrus, right caudate, right olfactory cortex, right inferior frontal gyrus, and triangular part. The most discriminating regions for treatment response prediction include left and right putamen, right pallidum, left hippocampus, right amygdala, right Caudate, left inferior frontal gyrus, triangular part, left insula, left lingual, and left rectus
4. DISCUSSION
In this study, we proposed a novel STGCN framework based on dynamic functional connectivity, which is demonstrated to successfully discriminate MDD patients from healthy controls and predict the treatment response of patients. To the best of our knowledge, this is the first study that simultaneously identifies and predicts treatment response of MDD using dynamic topologic features derived from resting‐state fMRI. The diagnosis accuracies are 84.14 and 83.93% across two study sites and the accuracy of treatment response prediction is as high as 89.63% for the Zhongda site. The performance of the proposed framework transcends that of other traditional algorithms, suggestive of its potential of being used clinically for diagnosis and treatment prediction.
As alluded to earlier, the current diagnosis of MDD primarily relies on patients' clinical manifestations and the treatment response is determined about a month posttreatment. In the recent decade, important progresses have been achieved in establishing robust neuroimaging biomarkers for individualized identification and treatment response prediction. Methodologically, the proposed method enhances the capabilities of diagnosis and treatment prediction by introducing a STGCN, whereas previous studies commonly used multivariate pattern analysis of static or dynamic functional connectivity in the brain network (Hultman et al., 2018; Ramirez‐Mahaluf et al., 2017), which have ignored topological features that could provide vital clues for diagnosis. Mechanistically, the enhanced performance of the STGCN framework we proposed may have derived from several technical innovations. Firstly, the STGCN approach could have outperformed the GCN method, which indicates the importance of the temporal fusion of dynamic functional connectivities. Secondly, the proposed SGAC module could have achieved higher accuracies than the traditional graph convolution module. In principle, the proposed convolution module could give larger weights to the important nodes with more contribution to the classification task, which could help improve feature learning on each dynamic functional connectivity. Thirdly, the performance of the proposed pooling approach was superior to traditional pooling methods on the clinical evaluations, in that the proposed anatomy prior graph pooling module could obtain more effective dimension reduction due to the hierarchical architecture of multiscale parcellations.
The clinical findings from the STGCN are that there are shared and specific brain regions of diagnosis and treatment, much to our expectations. Our experiments indicate that some basal nuclei including pallidum and putamen are not only involved in the pathogenesis of depression, but also related to the prognosis of the disease. The pallidum is an important brain structure that distinguishes disease and prognosis of MDD with a high contribution degree (Knowland et al., 2017). Physiologically, the pallidum is a major convergent point related to reward circuitry, which is critical to clinical manifestations of depression, such as anhedonia. Moreover, the pallidum is essential for antidepressant effects of ketamine (Yamanaka et al., 2014). Meanwhile, the putamen, as part of the striatum, is considered to be composed of the limbic, associative, and sensorimotor subregions, which also plays a major role in emotional/motivational functions and reward processing (Postuma & Dagher, 2006). In addition to these two structures, the present study also found that some other brain structures such as hippocampus, amygdala, and insula were important for distinguishing curative effects. In previous studies, decreased hippocampal and increased amygdala volumes were considered a potential marker in first‐episode MDD patients, which are positively correlated with the severity of depression (Frodl et al., 2002; van Eijndhoven et al., 2009). In this study, enhanced functional activity and connectivity in amygdala were found in remitted women depressive patients as well, which implicates that amygdala dysfunction is also an effective indicator of prognosis (Albert, Gau, Taylor, & Newhouse, 2017). Taken together, these findings suggest that the STGCN could provide a new strategy for finding imaging markers for the diagnosis and treatment of depression.
Finally, a few limitations of this work should be pointed out. As mentioned previously, the sample size used in this study is relatively large for learning discriminative features of diagnosis and treatment response for MDD. A larger size preferably from more diverse study sites will be undoubtedly beneficial to parameter optimizations and thus further increases in the accuracies of both diagnosis and treatment response prediction. Moreover, the current study only utilizes functional connectivity information derived from functional MRI. It is anticipated that multi‐modal imaging with added parameter dimensions, which will be included in our future studies, will further enhance the performance of the proposed framework. Lastly but not least importantly, the efficacy observation in the present study is made only 2 weeks posttreatment, so it is not possible to predict mid‐ and long‐term effects or the final outcome of the patients with MDD. In spite of these limitations, this study demonstrates that the proposed STGCN framework, which features dynamic functional connectivity, outperforms other classification algorithms in accurately diagnosing MDD and predicting early efficacy, which provides a promising future direction for effective management of MDD.
5. CONCLUSION
In this work, we have developed a novel STGCN framework to capture brain dynamic functional connectivity for diagnosis and treatment response prediction of MDD. The proposed framework can achieve superior performance for both the purposes. Our experiments with large clinical data sets suggest a high potential of spatiotemporal graph learning with dynamic functional connectivity in exploring biomarkers for effective clinical diagnosis and treatment response prediction of MDD. In addition, the proposed STGCN framework can also be adapted to investigate other brain diseases.
CONFLICT OF INTEREST
All the authors have no conflict of interest to declare.
ACKNOWLEDGMENTS
The research is supported by grant 2018ZX10201‐002 National Science and Technology Major Project of China, grant 31800825, 81971277, 31640028 National Natural Science Foundation of China and grant BE2019748 Natural Science Foundation of Jiangsu Province. This work is supported in part by grant 81830040 National Natural Science Key Foundation of China and grant 2018B030334001 Science and Technology Program of Guangdong Province. This work is supported in part by grant 2242020K40039 Fundamental Research Funds for the Central Universities. We thank all the patients and volunteers for participating in this study. We also wish to express gratitude to Professor Zhaohua Ding (Vanderbilt University) for his valuable suggestions.
Kong, Y. , Gao, S. , Yue, Y. , Hou, Z. , Shu, H. , Xie, C. , Zhang, Z. , & Yuan, Y. (2021). Spatio‐temporal graph convolutional network for diagnosis and treatment response prediction of major depressive disorder from functional connectivity. Human Brain Mapping, 42(12), 3922–3933. 10.1002/hbm.25529
Funding information National Science and Technology Major Project of China: 2018ZX10201‐002; National Natural Science Foundation of China, Grant/Award Numbers: 31800825, 81971277: 31640028; Natural Science Foundation of Jiangsu Province, Grant/Award Number: BE2019748; National Natural Science Key Foundation of China: 81830040; Science and Technology Program of Guangdong Province: 2018B030334001; Fundamental Research Funds for the Central Universities, Grant/Award Number: 2242020K40039
Contributor Information
Youyong Kong, Email: kongyouyong@seu.edu.cn.
Yonggui Yuan, Email: yygylh2000@sina.com.
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
REFERENCE
- Albert, K. , Gau, V. , Taylor, W. D. , & Newhouse, P. A. (2017). Attention bias in older women with remitted depression is associated with enhanced amygdala activity and functional connectivity. Journal of Affective Disorders, 210, 49–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badrinarayanan, V. , Kendall, A. , & Cipolla, R. (2017). SegNet: A deep convolutional encoder‐decoder architecture for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 39, 2481–2495. [DOI] [PubMed] [Google Scholar]
- Bao, F. , Deng, Y. , Kong, Y. Y. , Ren, Z. Q. , Suo, J. L. , & Dai, Q. H. (2020). Learning deep landmarks for imbalanced classification. IEEE Transactions on Neural Networks and Learning Systems, 31, 2691–2704. [DOI] [PubMed] [Google Scholar]
- Bauer, M. , Severus, E. , Kohler, S. , Whybrow, P. C. , Angst, J. , Moller, H. J. , & Wfsbp Task Force on Treatment Guidelines for Unipolar Depressive D . (2015). World Federation of Societies of biological psychiatry (WFSBP) guidelines for biological treatment of unipolar depressive disorders. Part 2: Maintenance treatment of major depressive disorder‐update 2015. The World Journal of Biological Psychiatry, 16, 76–95. [DOI] [PubMed] [Google Scholar]
- Bhaumik, R. , Jenkins, L. M. , Gowins, J. R. , Jacobs, R. H. , Barba, A. , Bhaumik, D. K. , & Langenecker, S. A. (2017). Multivariate pattern analysis strategies in detection of remitted major depressive disorder using resting state functional connectivity. Neuroimage‐Clinical, 16, 390–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, J. L. , Wang, L. F. , Meng, G. F. , Zhang, Q. , Xiang, S. M. , & Pan, C. H. (2020). Local‐aggregation graph networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 42, 2874–2886. [DOI] [PubMed] [Google Scholar]
- Dwyer, J. B. , Aftab, A. , Radhakrishnan, R. , Widge, A. , Rodriguez, C. I. , Carpenter, L. L. , … Biomarkers APACoRTFoN, Treatments . (2020). Hormonal treatments for major depressive disorder: State of the art. The American Journal of Psychiatry, 177, 686–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- First, M. B. , Spitzer, R. L. , Gibbon, M. , & Williams, J. B. W. (1997). Structured clinical interview for DSM‐IV Axis I disorders (SCID‐I). Washington, D.C.: American Psychiatric Association. [Google Scholar]
- Frodl, T. , Meisenzahl, E. M. , Zetzsche, T. , Born, C. , Groll, C. , Jager, M. , … Moller, H. J. (2002). Hippocampal changes in patients with a first episode of major depression. The American Journal of Psychiatry, 159, 1112–1118. [DOI] [PubMed] [Google Scholar]
- Hou, Z. , Kong, Y. , He, X. , Yin, Y. , Zhang, Y. , & Yuan, Y. (2018). Increased temporal variability of striatum region facilitating the early antidepressant response in patients with major depressive disorder. Progress in Neuro‐Psychopharmacology & Biological Psychiatry, 85, 39–45. [DOI] [PubMed] [Google Scholar]
- Hou, Z. H. , Kong, Y. Y. , Yin, Y. Y. , Zhang, Y. Q. , & Yuan, Y. G. (2021). Identification of first‐episode unmedicated major depressive disorder using pretreatment features of dominant coactivation patterns. Progress in Neuro‐Psychopharmacology, 104, 110038. [DOI] [PubMed] [Google Scholar]
- Hultman, R. , Ulrich, K. , Sachs, B. D. , Blount, C. , Carlson, D. E. , Ndubuizu, N. , … Dzirasa, K. (2018). Brain‐wide electrical spatiotemporal dynamics encode depression vulnerability. Cell, 173(166–180), e114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang, J. , Xu, C. , Cui, Z. , Zhang, T. , Zheng, W. , & Yang, J. (2020). Walk‐steered convolution for graph classification. IEEE Transactions on Neural Networks and Learning Systems, 31(11), 4553–4566. [DOI] [PubMed] [Google Scholar]
- Kaiser, R. H. , Andrews‐Hanna, J. R. , Wager, T. D. , & Pizzagalli, D. A. (2015). Large‐scale network dysfunction in major depressive disorder: A meta‐analysis of resting‐state functional connectivity. JAMA Psychiatry, 72, 603–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knowland, D. , Lilascharoen, V. , Pacia, C. P. , Shin, S. , Wang, E. H. , & Lim, B. K. (2017). Distinct ventral Pallidal neural populations mediate separate symptoms of depression. Cell, 170(284–297), e218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ktena, S. I. , Parisot, S. , Ferrante, E. , Rajchl, M. , Lee, M. , Glocker, B. , & Rueckert, D. (2018). Metric learning with spectral graph convolutions on brain connectivity networks. NeuroImage, 169, 431–442. [DOI] [PubMed] [Google Scholar]
- Leucht, S. , Fennema, H. , Engel, R. , Kaspers‐Janssen, M. , Lepping, P. , & Szegedi, A. (2013). What does the HAMD mean? Journal of Affective Disorders, 148, 243–248. [DOI] [PubMed] [Google Scholar]
- Liu, J. , Li, M. , Lan, W. , Wu, F. X. , Pan, Y. , & Wang, J. X. (2018). Classification of Alzheimer's disease using whole brain hierarchical network. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 15, 624–632. [DOI] [PubMed] [Google Scholar]
- Luo, L. K. , Li, Q. , You, W. F. , Wang, Y. X. , Tang, W. J. , Li, B. , … Gong, Q. Y. (2021). Altered brain functional network dynamics in obsessive‐compulsive disorder. Human Brain Mapping, 42, 2061–2076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petar Velickovic GC, Casanova Arantxa, Romero Adriana, Lio Pietro, and Bengio Yoshua. (2018) Graph Attention Networks. In: International Conference on Learning Representations.
- Postuma, R. B. , & Dagher, A. (2006). Basal ganglia functional connectivity based on a meta‐analysis of 126 positron emission tomography and functional magnetic resonance imaging publications. Cerebral Cortex, 16, 1508–1521. [DOI] [PubMed] [Google Scholar]
- Ramirez‐Mahaluf, J. P. , Roxin, A. , Mayberg, H. S. , & Compte, A. (2017). A computational model of major depression: The role of glutamate dysfunction on Cingulo‐frontal network dynamics. Cerebral Cortex, 27, 660–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosa, M. J. , Portugal, L. , Hahn, T. , Fallgatter, A. J. , Garrido, M. I. , Shawe‐Taylor, J. , & Mourao‐Miranda, J. (2015). Sparse network‐based models for patient classification using fMRI. NeuroImage, 105, 493–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekhon, S. , Patel, J. , & Sapra, A. (2020). Late onset depression. Island (FL): StatPearls Treasure. [Google Scholar]
- Sendi, M. S. E. , Zendehrouh, E. , Sui, J. , Fu, Z. , Zhi, D. , Lv, L. , … Calhoun, V. (2021). Aberrant dynamic functional connectivity of default mode network predicts symptom severity in major depressive disorder. Brain Connectivity, brain.2020.0748. 10.1089/brain.2020.0748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan, K. E. , Bach, D. R. , Fletcher, P. C. , Flint, J. , Frank, M. J. , Friston, K. J. , … Breakspear, M. (2016). Charting the landscape of priority problems in psychiatry, part 1: Classification and diagnosis. Lancet Psychiatry, 3, 77–83. [DOI] [PubMed] [Google Scholar]
- Valsesia, D. , Fracastoro, G. , & Magli, E. (2020). Deep graph‐convolutional image Denoising. IEEE Transactions on Image Processing, 29, 8226–8237. [DOI] [PubMed] [Google Scholar]
- van Eijndhoven, P. , van Wingen, G. , van Oijen, K. , Rijpkema, M. , Goraj, B. , Jan Verkes, R. , … Tendolkar, I. (2009). Amygdala volume marks the acute state in the early course of depression. Biological Psychiatry, 65, 812–818. [DOI] [PubMed] [Google Scholar]
- Yamanaka, H. , Yokoyama, C. , Mizuma, H. , Kurai, S. , Finnema, S. J. , Halldin, C. , … Onoe, H. (2014). A possible mechanism of the nucleus accumbens and ventral pallidum 5‐HT1B receptors underlying the antidepressant action of ketamine: A PET study with macaques. Translational Psychiatry, 4, e342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao, D. , Sui, J. , Wang, M. , Yang, E. , Jiaerken, Y. , Luo, N. , … Shen, D. (2021). A mutual multi‐scale triplet graph convolutional network for classification of brain disorders using functional or structural connectivity. IEEE Transactions on Medical Imaging, 40(4), 1279–1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky, A. , Fornito, A. , Cocchi, L. , Gollo, L. L. , & Breakspear, M. (2014). Time‐resolved resting‐state brain networks. Proceedings of the National Academy of Sciences of the United States of America, 111, 10341–10346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, G. , Cai, B. , Zhang, A. , Stephen, J. M. , Wilson, T. W. , Calhoun, V. D. , & Wang, Y. P. (2020). Estimating dynamic functional brain connectivity with a sparse hidden Markov model. IEEE Transactions on Medical Imaging, 39, 488–498. [DOI] [PubMed] [Google Scholar]
- Zhang, Y. , Kong, Y. Y. , Wu, J. S. , Coatrieux, G. , & Shu, H. Z. (2019). Brain tissue segmentation based on graph convolutional networks (pp. 1470–1474). Taipei, Taiwan: IEEE International Conference on Image Processing. [Google Scholar]
- Zhao, J. , Huang, J. , Zhi, D. , Yan, W. , Ma, X. , Yang, X. , … Sui, J. (2020). Functional network connectivity (FNC)‐based generative adversarial network (GAN) and its applications in classification of mental disorders. Journal of Neuroscience Methods, 341, 108756. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.


