Abstract
We classify gapped topological superconducting (TSC) phases of one-dimensional quantum wires with local magnetic symmetries, in which the time-reversal symmetry  is broken, but its combinations with certain crystalline symmetries, such as
is broken, but its combinations with certain crystalline symmetries, such as 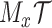 ,
, 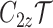 ,
,  and
and  , are preserved. Our results demonstrate that an equivalent BDI class TSC can be realized in the
, are preserved. Our results demonstrate that an equivalent BDI class TSC can be realized in the 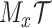 or
or 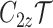 superconducting wire, which is characterized by a chiral Zc invariant. More interestingly, we also find two types of totally new TSC phases in the
superconducting wire, which is characterized by a chiral Zc invariant. More interestingly, we also find two types of totally new TSC phases in the 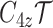 and
and  superinducting wires, which are beyond the known AZ class, and are characterized by a helical Zh invariant and Zh⊕Zc invariants, respectively. In the Zh TSC phase, Z pairs of Majorana zero modes (MZMs) are protected at each end. In the
superinducting wires, which are beyond the known AZ class, and are characterized by a helical Zh invariant and Zh⊕Zc invariants, respectively. In the Zh TSC phase, Z pairs of Majorana zero modes (MZMs) are protected at each end. In the 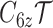 case, the MZMs can be either chiral or helical, and even helical-chiral coexisting. The minimal models preserving
case, the MZMs can be either chiral or helical, and even helical-chiral coexisting. The minimal models preserving  or
or 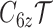 symmetry are presented to illustrate their novel TSC properties and MZMs.
symmetry are presented to illustrate their novel TSC properties and MZMs.
Keywords: topological superconductor, magnetic symmetry, Majorana zero mode, superconducting wire
Topological superconducting phases of one-dimensional quantum wires with local magnetic symmetries are classified and new types of Majorana modes are discussed.
INTRODUCTION
Topological superconductors (TSCs) are new kinds of topological quantum states, which are fully superconducting gapped in the bulk but support gapless excitations called Majorana zero modes (MZMs) at the boundaries [1–5]. As analogues of the famous Majorana fermions [6], MZMs are their own antiparticles, and are proposed as the qubits of topological quantum computation because of their nonlocal correlation and non-Abelian statistic nature [7–10]. Hence, searching for TSC materials with MZMs is now an important topic in condensed matter physics, and a series of schemes have been proposed in the last decade, including the proximity effect on the surface of topological insulators [11–16] and the recently predicted intrinsic superconducting topological materials [17–25].
To identify whether a superconductor is topologically nontrivial, we should first ascertain to what topological classification it belongs. The topological classification can be highly enriched by symmetries, including time-reversal symmetry 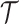 , particle-hole symmetry
, particle-hole symmetry 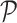 and especially the crystalline symmetries [26–35]. The topology for noninteracting Hamiltonians of the 10 Altland–Zirnbauer (AZ) classes with or without
and especially the crystalline symmetries [26–35]. The topology for noninteracting Hamiltonians of the 10 Altland–Zirnbauer (AZ) classes with or without 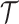 and
and 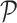 has been well classified [26,27]. Particularly, the Bogoliubov–de Gennes (BdG) Hamiltonians of the one-dimensional (1D) superconductors, with
has been well classified [26,27]. Particularly, the Bogoliubov–de Gennes (BdG) Hamiltonians of the one-dimensional (1D) superconductors, with 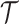 breaking or preserving, belong to the D and DIII classes, respectively. In both cases we only have the Z2 classification. In addition to these local symmetries, crystalline symmetries are considered for each AZ class to generalize the topological classification [28–31], and the topological crystalline superconductors protected by mirror reflection symmetry [32,33] or rotational symmetries [34,35] have been proposed. Furthermore, the TSC phase protected by the magnetic symmetries
breaking or preserving, belong to the D and DIII classes, respectively. In both cases we only have the Z2 classification. In addition to these local symmetries, crystalline symmetries are considered for each AZ class to generalize the topological classification [28–31], and the topological crystalline superconductors protected by mirror reflection symmetry [32,33] or rotational symmetries [34,35] have been proposed. Furthermore, the TSC phase protected by the magnetic symmetries 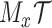 and
and 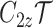 has been discussed in [34,36–38]. Nevertheless, the topological classification of superconductors with general magnetic symmetries is still an open question, and the corresponding theoretical analysis is necessary for understanding and searching for new magnetic TSC materials and MZMs.
has been discussed in [34,36–38]. Nevertheless, the topological classification of superconductors with general magnetic symmetries is still an open question, and the corresponding theoretical analysis is necessary for understanding and searching for new magnetic TSC materials and MZMs.
In this paper, we focus on the topological phases of gapped superconducting wires with local magnetic symmetries (LMSs), in which 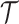 is broken, but its combinations with certain crystalline symmetries—those leaving each site invariant, including
is broken, but its combinations with certain crystalline symmetries—those leaving each site invariant, including 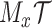 ,
, 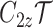 ,
, 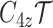 and
and 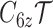 —are preserved. Our analysis shows that, with
—are preserved. Our analysis shows that, with 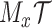 or
or 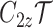 symmetry, an effective BDI class TSC can be realized, which is characterized by a chiral Zc topological invariant and protects an integer number of MZMs at each end. Remarkably, two totally new TSC phases are discussed in the superconducting wire with
symmetry, an effective BDI class TSC can be realized, which is characterized by a chiral Zc topological invariant and protects an integer number of MZMs at each end. Remarkably, two totally new TSC phases are discussed in the superconducting wire with 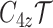 or
or 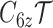 symmetry. In the
symmetry. In the  case, the BdG Hamiltonian is characterized by a helical Zh invariant, which can protect Z pairs of MZMs at each end. The BdG Hamiltonian with
case, the BdG Hamiltonian is characterized by a helical Zh invariant, which can protect Z pairs of MZMs at each end. The BdG Hamiltonian with  symmetry possesses Zh⊕Zc invariants, which means that the helical and chiral MZMs can coexist in a single wire system. The minimal models with the LMSs
symmetry possesses Zh⊕Zc invariants, which means that the helical and chiral MZMs can coexist in a single wire system. The minimal models with the LMSs 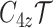 and
and  are presented separately, in which the TSC with helical MZMs and the TSC with helical-chiral coexisting MZMs are discussed. Our results may facilitate the ongoing search for novel TSCs.
are presented separately, in which the TSC with helical MZMs and the TSC with helical-chiral coexisting MZMs are discussed. Our results may facilitate the ongoing search for novel TSCs.
TOPOLOGICAL CLASSIFICATION OF GAPPED SUPERCONDUCTING WIRE
We first introduce the LMSs for a magnetic superconducting wire along the 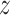 direction. Among the 1D space groups (the so-called rod group) [39], the local symmetry operators include the mirror reflection Mx and the n-fold rotation Cnz with n = 2, 3, 4, 6. Combined with
direction. Among the 1D space groups (the so-called rod group) [39], the local symmetry operators include the mirror reflection Mx and the n-fold rotation Cnz with n = 2, 3, 4, 6. Combined with 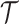 , we obtain four types of LMSs,
, we obtain four types of LMSs, 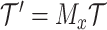 ,
, 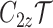 ,
, 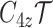 and
and 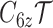 , as tabulated in Table 1. We consider a 1D BdG Hamiltonian preserving
, as tabulated in Table 1. We consider a 1D BdG Hamiltonian preserving 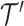 . Note that the operation of
. Note that the operation of  does not change the positions of electrons. Hence, it acts on the BdG Hamiltonian like a time-reversal operator
does not change the positions of electrons. Hence, it acts on the BdG Hamiltonian like a time-reversal operator
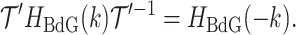 |
(1) |
Here, LMS  takes the form
takes the form 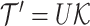 with
with 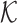 being the complex conjugate operator and U being a unitary matrix determined by the spatial operation and spin flipping. We employ the convention that
being the complex conjugate operator and U being a unitary matrix determined by the spatial operation and spin flipping. We employ the convention that 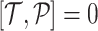 and set
and set 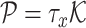 , where the Pauli matrix τx acts on the particle-hole degree of freedom. Combining
, where the Pauli matrix τx acts on the particle-hole degree of freedom. Combining 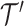 and
and 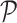 leads to a chiral symmetry
leads to a chiral symmetry 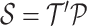 . Both
. Both 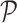 and
and 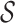 act on the BdG Hamiltonian as
act on the BdG Hamiltonian as
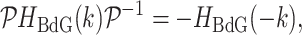 |
(2) |
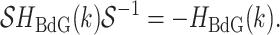 |
(3) |
Table 1.
The topological classification of the 1D gapped superconducting systems with the LMSs 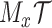 ,
, 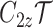 ,
, 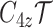 and
and 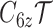 , respectively. 2×AIII form a helical Zh classification.
, respectively. 2×AIII form a helical Zh classification.
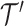
|
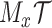
|

|

|
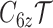
|
|---|---|---|---|---|
| (n = 2) | (n = 2) | (n = 4) | (n = 6) | |

|
1 | 1 | −1 | 1 |

|
1 | 1 | 1 | 1 |
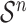
|
1 | 1 | −1 | 1 |
| Invariant | Z c | Z c | Z h | Z h ⊕Zc |
| (BDI) | (BDI) | (2×AIII) | (2×AIII ⊕ BDI) |
The chiral symmetry 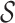 has a series of eigenvalue pairs ±s1, ±s2, … and it can take a block-diagonal form as
has a series of eigenvalue pairs ±s1, ±s2, … and it can take a block-diagonal form as 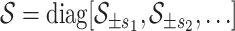 , where the subscript ±s1 denotes the direct sum of eigenvector spaces |s1〉 and | − s1〉. The anticommute relation (3) means that HBdG(k) can be block diagonalized according to the eigenvalues of
, where the subscript ±s1 denotes the direct sum of eigenvector spaces |s1〉 and | − s1〉. The anticommute relation (3) means that HBdG(k) can be block diagonalized according to the eigenvalues of  . In other words, HBdG(k) can adopt the form
. In other words, HBdG(k) can adopt the form 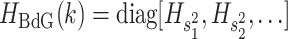 . Hence, the topological classification of the whole Hamiltonian is decomposed into examining the topology of each block and their compatibility. For each block Hamiltonian
. Hence, the topological classification of the whole Hamiltonian is decomposed into examining the topology of each block and their compatibility. For each block Hamiltonian 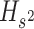 , its topology is equivalent to either the BDI or the AIII class, depending on the chiral symmetry eigenvalue s. To be specific, when s is a real number,
, its topology is equivalent to either the BDI or the AIII class, depending on the chiral symmetry eigenvalue s. To be specific, when s is a real number, 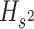 is invariant under
is invariant under 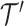 or
or 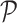 , which means that it belongs to the BDI class and possesses a Z invariant expressed as
, which means that it belongs to the BDI class and possesses a Z invariant expressed as  = Ns − N−s, where the N±s are the numbers of MZMs with chiral symmetry eigenvalue ±s, respectively. Additionally, when s is a complex number,
= Ns − N−s, where the N±s are the numbers of MZMs with chiral symmetry eigenvalue ±s, respectively. Additionally, when s is a complex number, 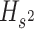 is transformed into
is transformed into  under
under 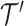 or
or 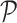 . Hence, the
. Hence, the 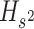 (
(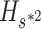 ) belongs to the AIII class that is characterized by a Z invariant
) belongs to the AIII class that is characterized by a Z invariant 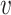 = Ns − N−s (
= Ns − N−s (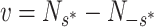 ), which is equal to the number of MZM pairs on each wire end.
), which is equal to the number of MZM pairs on each wire end.
We next consider the compatibility between the different MZMs possessing different 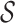 eigenvalues. To do this, we introduce a coupling term m|s1〉〈s2|, which satisfies the chiral symmetry, i.e.
eigenvalues. To do this, we introduce a coupling term m|s1〉〈s2|, which satisfies the chiral symmetry, i.e. 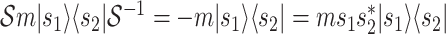 . Here m is a perturbation parameter, and |s1〉 and |s2〉 are the eigenstates of
. Here m is a perturbation parameter, and |s1〉 and |s2〉 are the eigenstates of 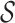 . Then we see that m can be nonzero only when
. Then we see that m can be nonzero only when 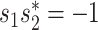 , which means that MZMs within one block having chiral eigenvalues s and −s can couple to each other and be eliminated. However, MZMs from different blocks are noninterfering due to the protection of
, which means that MZMs within one block having chiral eigenvalues s and −s can couple to each other and be eliminated. However, MZMs from different blocks are noninterfering due to the protection of 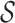 . Therefore, the topological classification of the whole BdG Hamiltonian is determined by the summation of the topology for each block. We summarize the topological classification of 1D gapped superconductors in Table 1 and analyse each case in the following.
. Therefore, the topological classification of the whole BdG Hamiltonian is determined by the summation of the topology for each block. We summarize the topological classification of 1D gapped superconductors in Table 1 and analyse each case in the following.
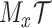 and
and 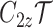 cases. These two cases are equivalent to the BDI class with
cases. These two cases are equivalent to the BDI class with 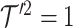 and
and 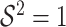 . The chiral topological invariant
. The chiral topological invariant  = N1 − N−1 ∈ Z is given by the winding number [5,26]
= N1 − N−1 ∈ Z is given by the winding number [5,26]
Here W(k) is a unitary matrix that diagonalizes the BdG Hamiltonian and θ(k) is the phase angle of Det[W(k)]. The identity Tr[ln(W)] = ln(Det[W]) is used to derive the above equation. These results agree well with the conclusions reached in previous studies [34,36–38,40,41].
(4) 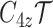 case. The chiral symmetry satisfies
case. The chiral symmetry satisfies 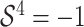 and has eigenvalues ±e±iπ/4 (see Fig. 1). We can conclude that the topological invariants are given by
and has eigenvalues ±e±iπ/4 (see Fig. 1). We can conclude that the topological invariants are given by 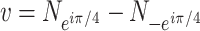 (or
(or 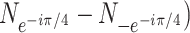 . The TSC phase is hence characterized by the helical topological invariant
. The TSC phase is hence characterized by the helical topological invariant 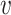 ∈ Z, which means that the MZMs always appear in Kramers pairs. This is obviously different from the chiral Z invariant in the BDI class, in which the MZMs can arise one by one as Z increases. To distinguish the chiral Z and helical Z invariants, we use Zc and Zh in the following. The Zh TSC phase of the
∈ Z, which means that the MZMs always appear in Kramers pairs. This is obviously different from the chiral Z invariant in the BDI class, in which the MZMs can arise one by one as Z increases. To distinguish the chiral Z and helical Z invariants, we use Zc and Zh in the following. The Zh TSC phase of the 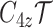 -preserving wire can be understood from the following perspective. The BdG Hamiltonian can be block diagonalized into two sectors according to the eigenvalues ±i of
-preserving wire can be understood from the following perspective. The BdG Hamiltonian can be block diagonalized into two sectors according to the eigenvalues ±i of 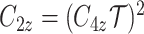 as Hi(k)⊕H−i(k). Both
as Hi(k)⊕H−i(k). Both  and
and 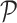 can map these two sectors to each other. However, their combination, i.e. the chiral symmetry
can map these two sectors to each other. However, their combination, i.e. the chiral symmetry 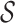 , keeps each sector invariant. As a consequence, each sector belongs to the AIII class, whose Zc topological invariant can be calculated by exploiting (4). Yielding to the
, keeps each sector invariant. As a consequence, each sector belongs to the AIII class, whose Zc topological invariant can be calculated by exploiting (4). Yielding to the 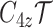 symmetry, the Zc invariants of two sectors must be equal, which finally gives a Zh invariant for the whole BdG Hamiltonian. That is, the topological invariant
symmetry, the Zc invariants of two sectors must be equal, which finally gives a Zh invariant for the whole BdG Hamiltonian. That is, the topological invariant 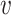 is given by the winding number of each C2
is given by the winding number of each C2 eigenvalue sector as defined in (4).
eigenvalue sector as defined in (4).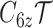 case. We have
case. We have  and
and 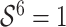 . As illustrated in Fig. 1, the chiral symmetry has eigenvalues ±e±iπ/3, ±1. The topology is characterized by Zh⊕Zc invariants that are given by
. As illustrated in Fig. 1, the chiral symmetry has eigenvalues ±e±iπ/3, ±1. The topology is characterized by Zh⊕Zc invariants that are given by 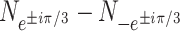 and N1 − N−1, respectively. Similar to the
and N1 − N−1, respectively. Similar to the  case, the BdG Hamiltonian can be block diagonalized as
case, the BdG Hamiltonian can be block diagonalized as  according to the eigenvalues e±i2π/3, 1 of
according to the eigenvalues e±i2π/3, 1 of 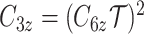 . The
. The 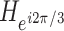 and
and 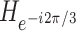 sectors both belong to the AIII class, forming a Zh classification together, whereas the H1 sector itself forms a Zc classification (i.e. BDI class) with
sectors both belong to the AIII class, forming a Zh classification together, whereas the H1 sector itself forms a Zc classification (i.e. BDI class) with 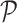 and an effective
and an effective 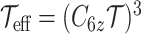 . Therefore, the topology of the whole BdG Hamiltonian is classified by Zh⊕Zc, whose topological invariants (
. Therefore, the topology of the whole BdG Hamiltonian is classified by Zh⊕Zc, whose topological invariants ( h,
h,  c) are given by the winding numbers of the
c) are given by the winding numbers of the  and H1 sectors, respectively. As a consequence, in a 1D superconducting wire with the LMS
and H1 sectors, respectively. As a consequence, in a 1D superconducting wire with the LMS 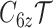 , the helical and chiral MZMs can coexist. Such novel TSC phase stimulate further interests in the manipulation of such helical-chiral coexisting MZMs [42–44].
, the helical and chiral MZMs can coexist. Such novel TSC phase stimulate further interests in the manipulation of such helical-chiral coexisting MZMs [42–44].
Figure 1.

The eigenvalues of 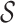 and their transformations in the
and their transformations in the 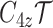 and
and 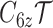 cases. Complex conjugating partners s and s* are related by the LMSs and always coexist. A perturbation term can be introduced to couple the chiral states with opposite eigenvalues, as illustrated by the red, blue and black double-head arrows.
cases. Complex conjugating partners s and s* are related by the LMSs and always coexist. A perturbation term can be introduced to couple the chiral states with opposite eigenvalues, as illustrated by the red, blue and black double-head arrows.
MODEL REALIZATION
To illustrate the TSC phase with the LMS  , we construct a 1D antiferromagnetic chain along the
, we construct a 1D antiferromagnetic chain along the 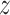 direction, as shown in Fig. 2(a), where each unit cell contains four subsites and each subsite is occupied by one spin polarized s orbital. We consider that the intra-cell coupling between the same spin states is much larger than the spin-orbit coupling, and thus the four orbitals are well split into two double-degenerate manifolds, as illustrated in Fig. 2(a). More details of the full model have been given in the online supplementary material. Here, to capture the topological phase of the model, we take the |px, ↑〉 and |py, ↓〉 subspaces to build an effective tight-binding model. Up to the nearest-neighbor hopping, it can be written as
direction, as shown in Fig. 2(a), where each unit cell contains four subsites and each subsite is occupied by one spin polarized s orbital. We consider that the intra-cell coupling between the same spin states is much larger than the spin-orbit coupling, and thus the four orbitals are well split into two double-degenerate manifolds, as illustrated in Fig. 2(a). More details of the full model have been given in the online supplementary material. Here, to capture the topological phase of the model, we take the |px, ↑〉 and |py, ↓〉 subspaces to build an effective tight-binding model. Up to the nearest-neighbor hopping, it can be written as
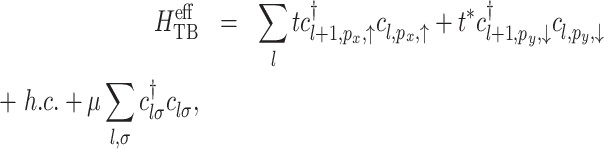 |
(5) |
where t = |t|eiα is the complex hopping, μ is the chemical potential and σ acts on the orbital degree of freedom of the |px, ↑〉 and |py, ↓〉 states. The 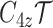 is given by
is given by  . Note that the hopping terms between opposite spins are prohibited by the C2
. Note that the hopping terms between opposite spins are prohibited by the C2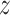 symmetry. The s-wave pairing Hamiltonian takes the form
symmetry. The s-wave pairing Hamiltonian takes the form
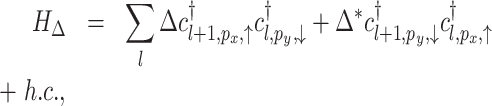 |
(6) |
with Δ = |Δ|eiφ. The pairing terms between the same spin are also prohibited by the C2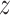 symmetry.
symmetry.
Figure 2.

(a) A  -preserving superconducting wire aligned along the
-preserving superconducting wire aligned along the  direction, in which the red and blue dots denote the spin up (+
direction, in which the red and blue dots denote the spin up (+ ) and spin down (−
) and spin down (−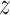 ) polarized s orbitals, respectively. The intra-cell coupling between the same spin orbitals is much larger than the spin-orbit coupling, which split the four states into one symmetric (SY) manifold and one antisymmetric (AS) manifold. Both manifolds are double degenerate. For simplicity, only the AS manifold is considered in our tight-binding model (5). (b) The topological phase diagram of (8) as the function of μ and δ, in which 0, ±1 are the winding numbers, μ is the chemical potential and δ = π/2 + φ − α is the phase difference between the coefficients of τy and τ
) polarized s orbitals, respectively. The intra-cell coupling between the same spin orbitals is much larger than the spin-orbit coupling, which split the four states into one symmetric (SY) manifold and one antisymmetric (AS) manifold. Both manifolds are double degenerate. For simplicity, only the AS manifold is considered in our tight-binding model (5). (b) The topological phase diagram of (8) as the function of μ and δ, in which 0, ±1 are the winding numbers, μ is the chemical potential and δ = π/2 + φ − α is the phase difference between the coefficients of τy and τ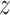 .
.
In the Nambu basis 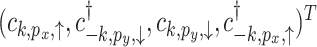 ,
,  and
and 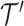 are given by
are given by 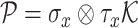 and
and  , respectively, which give
, respectively, which give 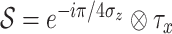 . The BdG Hamiltonian anticommutes with
. The BdG Hamiltonian anticommutes with 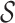 and takes a block-diagonal form as
and takes a block-diagonal form as
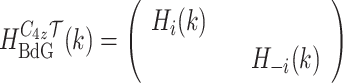 |
(7) |
with
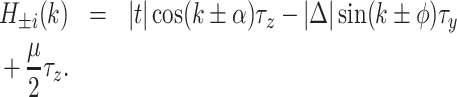 |
(8) |
Then the spectrum is given by
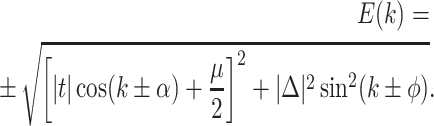 |
(9) |
Note that the two blocks in (7) are Kramers pairs related by the  symmetry and have the same winding number. A straightforward way to determine the topology is to calculate the winding number
symmetry and have the same winding number. A straightforward way to determine the topology is to calculate the winding number  using (4) for the upper or lower blocks. Here we provide a much simpler way to obtain
using (4) for the upper or lower blocks. Here we provide a much simpler way to obtain 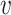 by analogizing the coefficients of the block Hamiltonians with elliptically polarized lights, whose electric field is described by Ex = Axcos (kz − ωt), Ey = Aycos (kz − ωt + δ). In the following we analyze the winding number of Hi(k), where the coefficients of the Pauli matrices are h
by analogizing the coefficients of the block Hamiltonians with elliptically polarized lights, whose electric field is described by Ex = Axcos (kz − ωt), Ey = Aycos (kz − ωt + δ). In the following we analyze the winding number of Hi(k), where the coefficients of the Pauli matrices are h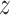 − μ/2 = |t|cos (k + α) and hy = |Δ|sin (k + φ). When |t||sin δ| > μ/2 (<μ/2), the parameter curve of hy(k) and h
− μ/2 = |t|cos (k + α) and hy = |Δ|sin (k + φ). When |t||sin δ| > μ/2 (<μ/2), the parameter curve of hy(k) and h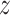 (k) will (not) wind around the zero point h
(k) will (not) wind around the zero point h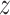 = hy = 0 (we assume that μ > 0 for simplicity), and the superconducting wire is in a topological nontrival (trivial) phase. Furthermore, when δ ∈ (0, π) [δ ∈ (−π, 0)], we have a left-handed (right-handed) parameter curve, and the topological phase is characterized by winding number +1 ( − 1). The phase diagram in the δ − μ parameter space is plotted in Fig. 2(b). We point out that, when next-nearest-neighbor hopping and pairing are considered, the competition with nearest-neighbor hopping and pairing gives rise to the opportunity for TSC phase with higher winding numbers.
= hy = 0 (we assume that μ > 0 for simplicity), and the superconducting wire is in a topological nontrival (trivial) phase. Furthermore, when δ ∈ (0, π) [δ ∈ (−π, 0)], we have a left-handed (right-handed) parameter curve, and the topological phase is characterized by winding number +1 ( − 1). The phase diagram in the δ − μ parameter space is plotted in Fig. 2(b). We point out that, when next-nearest-neighbor hopping and pairing are considered, the competition with nearest-neighbor hopping and pairing gives rise to the opportunity for TSC phase with higher winding numbers.
In the nontrivial TSC phase, the open quantum wire traps integer pairs of MZMs at its ends. By using t = 1, Δ = 1.3eiπ/3, μ = 0.2, we observe two pairs of MZMs in total on the open wire spectrum, as shown in Fig. 3(b), which is in contrast with the gapped bulk spectrum in Fig. 3(a). These MZMs can also be solved from the continuous low-energy model [45]. Here, we need only consider Hi(k) since the other block in (7), as well as its zero energy solution, can be obtained by a 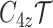 transformation. By assuming that the wire is placed on the
transformation. By assuming that the wire is placed on the  > 0 side, the low-energy massive Dirac Hamiltonian close to k = π/2 is given by
> 0 side, the low-energy massive Dirac Hamiltonian close to k = π/2 is given by
 |
(10) |
Its zero energy solution Ψ1 and the 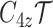 -related partner
-related partner 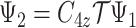 are given by
are given by
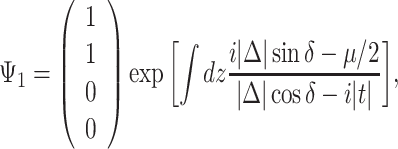 |
(11) |
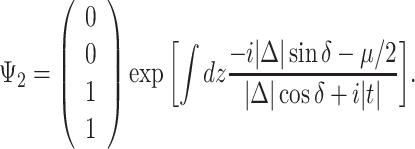 |
(12) |
These two states are the eigenstates of the chiral symmetry  with eigenvalues e±iπ/4, respectively. Therefore, they are immune to perturbations preserving
with eigenvalues e±iπ/4, respectively. Therefore, they are immune to perturbations preserving 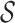 (and
(and  ). Their combinations give the
). Their combinations give the 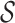 protected MZMs as γ1 = Ψ1 + Ψ2 and γ2 = i(Ψ1 − Ψ2).
protected MZMs as γ1 = Ψ1 + Ψ2 and γ2 = i(Ψ1 − Ψ2).
Figure 3.

The bulk spectrum and MZMs in the  -preserving TSC model. (a) The gapped bulk spectrum of the
-preserving TSC model. (a) The gapped bulk spectrum of the  -preserving TSC phase with t = 1, Δ = 1.3eiπ/3, μ = 0.2. (b) The corresponding spectrum of (a) with an open boundary on both sides, in which four MZMs appear at zero energy.
-preserving TSC phase with t = 1, Δ = 1.3eiπ/3, μ = 0.2. (b) The corresponding spectrum of (a) with an open boundary on both sides, in which four MZMs appear at zero energy.
The 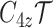 -preserving BdG Hamiltonian can be easily generalized to a
-preserving BdG Hamiltonian can be easily generalized to a  invariant quantum wire. For this purpose, we assume that the chiral symmetry is expressed as
invariant quantum wire. For this purpose, we assume that the chiral symmetry is expressed as  . The BdG Hamiltonian can then be written in three blocks
. The BdG Hamiltonian can then be written in three blocks  with
with
 |
(13) |
The first two blocks are Kramers pairs and take the same form as in (8), while the last block is transformed to itself under  or
or 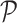 . For this BdG Hamiltonian, the topology is characterized by Zh⊕Zc numbers, which correspond to the number of helical and chiral MZMs, respectively. The topological phase diagram of the helical part Hamiltonian is the same as in Fig. 2(b). The chiral part is determined by the winding number of H1(k), which gives a nontrivial TSC phase when |t′| > μ/2.
. For this BdG Hamiltonian, the topology is characterized by Zh⊕Zc numbers, which correspond to the number of helical and chiral MZMs, respectively. The topological phase diagram of the helical part Hamiltonian is the same as in Fig. 2(b). The chiral part is determined by the winding number of H1(k), which gives a nontrivial TSC phase when |t′| > μ/2.
CONCLUSION
We have classified the TSC phases of quantum wires with LMSs. In the case of 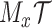 or
or 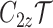 , an equivalent BDI class TSC can be realized [37,38,40]. More importantly, we find two new types of TSC phases in the superconducting wire with
, an equivalent BDI class TSC can be realized [37,38,40]. More importantly, we find two new types of TSC phases in the superconducting wire with 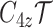 or
or 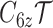 , which are beyond the already known AZ classes and can be characterized by Zh or Zh⊕Zc topological invariants, respectively. These results not only enrich the variety of the 1D TSC, but also provide luxuriant building blocks for the construction of new type 2D and 3D TSCs, by following the general method proposed in [46]. For example, one can couple the 1D TSCs in the y direction to construct a 2D TSC. The high symmetry lines ky = 0 and ky = π in momentum space preserve the 1D LMS. With proper parameters, the ky = 0 and ky = π lines can belong to distinct topological phases, and result in the gapless propagating Majorana edge states connecting the conducting bands and valence bands. The superconductivity and antiferromagnetism coexisting SmOFeAs [47,48] with a proper magnetic configuration satisfying C4
, which are beyond the already known AZ classes and can be characterized by Zh or Zh⊕Zc topological invariants, respectively. These results not only enrich the variety of the 1D TSC, but also provide luxuriant building blocks for the construction of new type 2D and 3D TSCs, by following the general method proposed in [46]. For example, one can couple the 1D TSCs in the y direction to construct a 2D TSC. The high symmetry lines ky = 0 and ky = π in momentum space preserve the 1D LMS. With proper parameters, the ky = 0 and ky = π lines can belong to distinct topological phases, and result in the gapless propagating Majorana edge states connecting the conducting bands and valence bands. The superconductivity and antiferromagnetism coexisting SmOFeAs [47,48] with a proper magnetic configuration satisfying C4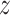 T symmetry is a possible material to study the 1D TSC phase on its high-symmetry lines.
T symmetry is a possible material to study the 1D TSC phase on its high-symmetry lines.
Supplementary Material
Acknowledgements
The authors thank Chaoxing Liu for valuable discussions.
Contributor Information
Jinyu Zou, Wuhan National High Magnetic Field Center & School of Physics, Huazhong University of Science and Technology, Wuhan 430074, China.
Qing Xie, Wuhan National High Magnetic Field Center & School of Physics, Huazhong University of Science and Technology, Wuhan 430074, China.
Zhida Song, Department of Physics, Princeton University, Princeton, NJ 08544, USA.
Gang Xu, Wuhan National High Magnetic Field Center & School of Physics, Huazhong University of Science and Technology, Wuhan 430074, China.
FUNDING
This work was supported by the National Key Research and Development Program of China (2018YFA0307000) and the National Natural Science Foundation of China (11874022).
AUTHOR CONTRIBUTIONS
Z.-D.S. and G.X. proposed the project. J.-Y.Z. carried out the topological classification and conceived the model. J.-Y.Z., Q.X., Z.-D.S. and G.X. analyzed the results. All authors contributed to the manuscript writing.
Conflict of interest statement. None declared.
REFERENCES
- 1. Kitaev AY. Unpaired Majorana fermions in quantum wires. Phys Usp 2001; 44: 131–6. [Google Scholar]
- 2. Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys 2011; 83: 1057–110. [Google Scholar]
- 3. Sato M, Tanaka Y, Yada Ket al. Topology of Andreev bound states with flat dispersion. Phys Rev B 2011; 83: 224511. [Google Scholar]
- 4. Ando Y, Fu L. Topological crystalline insulators and topological superconductors: from concepts to materials. Annu Rev Condens Matter Phys 2015; 6: 361–81. [Google Scholar]
- 5. Sato M, Ando Y. Topological superconductors: a review. Rep Prog Phys 2017; 80: 076501. [DOI] [PubMed] [Google Scholar]
- 6. Majorana E. Teoria simmetrica dell'elettrone e del positrone. Nuovo Cim 2008; 14: 171. [Google Scholar]
- 7. Ivanov DA. Non-abelian statistics of half-quantum vortices in p-wave superconductors. Phys Rev Lett 2001; 86: 268–71. [DOI] [PubMed] [Google Scholar]
- 8. Kitaev AY. Fault-tolerant quantum computation by anyons. Ann Phys 2003; 303: 2–30. [Google Scholar]
- 9. Nayak C, Simon SH, Stern Aet al. Non-Abelian anyons and topological quantum computation. Rev Mod Phys 2008; 80: 1083–159. [Google Scholar]
- 10. Sato M, Fujimoto S. Majorana fermions and topology in superconductors. J Phys Soc Japan 2016; 85: 072001. [Google Scholar]
- 11. Fu L, Kane CL. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys Rev Lett 2008; 100: 096407. [DOI] [PubMed] [Google Scholar]
- 12. Qi XL, Hughes TL, Zhang SC. Chiral topological superconductor from the quantum Hall state. Phys Rev B 2010; 82: 184516. [Google Scholar]
- 13. Linder J, Tanaka Y, Yokoyama Tet al. Unconventional superconductivity on a topological insulator. Phys Rev Lett 2010; 104: 067001. [DOI] [PubMed] [Google Scholar]
- 14. Wang MX, Liu C, Xu JPet al. The coexistence of superconductivity and topological order in the Bi2Se3 thin films. Science 2012; 336: 52–5. [DOI] [PubMed] [Google Scholar]
- 15. Xu JP, Liu C, Wang MXet al. Artificial topological superconductor by the proximity effect. Phys Rev Lett 2014; 112: 217001. [Google Scholar]
- 16. Wang J, Zhou Q, Lian Bet al. Chiral topological superconductor and half-integer conductance plateau from quantum anomalous Hall plateau transition. Phys Rev B 2015; 92: 064520. [Google Scholar]
- 17. Fu L, Berg E. Odd-parity topological superconductors: theory and application to CuxBi2Se3. Phys Rev Lett 2010; 105: 097001. [DOI] [PubMed] [Google Scholar]
- 18. Hosur P, Ghaemi P, Mong Ret al. Majorana modes at the ends of superconductor vortices in doped topological insulators. Phys Rev Lett 2011; 107: 097001. [DOI] [PubMed] [Google Scholar]
- 19. Tanaka Y, Sato M, Nagaosa N. Symmetry and topology in superconductors -odd-frequency pairing and edge states. J Phys Soc Japan 2012; 81: 011013. [Google Scholar]
- 20. Fu L. Odd-parity topological superconductor with nematic order: application to CuxBi2Se3. Phys Rev B 2014; 90: 100509. [DOI] [PubMed] [Google Scholar]
- 21. Hosur P, Dai X, Fang Zet al. Time-reversal-invariant topological superconductivity in doped Weyl semimetals. Phys Rev B 2014; 90: 045130. [Google Scholar]
- 22. Wang Z, Zhang P, Xu Get al. Topological nature of the FeSe0.5Te0.5 superconductor. Phys Rev B 2015; 92: 115119. [Google Scholar]
- 23. Xu G, Lian B, Tang Pet al. Topological superconductivity on the surface of Fe-based superconductors. Phys Rev Lett 2016; 117: 047001. [DOI] [PubMed] [Google Scholar]
- 24. Zhang P, Yaji K, Hashimoto Tet al. Observation of topological superconductivity on the surface of an iron-based superconductor. Science 2018; 360: 182–6. [DOI] [PubMed] [Google Scholar]
- 25. Wang D, Kong L, Fan Pet al. Evidence for Majorana bound states in an iron-based superconductor. Science 2018; 362: 333–5. [DOI] [PubMed] [Google Scholar]
- 26. Schnyder AP, Ryu S, Furusaki Aet al. Classification of topological insulators and superconductors in three spatial dimensions. Phys Rev B 2008; 78: 195125. [Google Scholar]
- 27. Ryu S, Schnyder AP, Furusaki Aet al. Topological insulators and superconductors: tenfold way and dimensional hierarchy. New J Phys 2010; 12: 065010. [Google Scholar]
- 28. Morimoto T, Furusaki A. Topological classification with additional symmetries from Clifford algebras. Phys Rev B 2013; 88: 125129. [Google Scholar]
- 29. Benalcazar WA, Teo JCY, Hughes TL. Classification of two-dimensional topological crystalline superconductors and Majorana bound states at disclinations. Phys Rev B 2014; 89: 224503. [DOI] [PubMed] [Google Scholar]
- 30. Chiu CK, Teo JCY, Schnyder APet al. Classification of topological quantum matter with symmetries. Rev Mod Phys 2016; 88: 035005. [Google Scholar]
- 31. Cornfeld E, Chapman A. Classification of crystalline topological insulators and superconductors with point group symmetries. Phys Rev B 2019; 99: 075105. [Google Scholar]
- 32. Zhang F, Kane CL, Mele EJ. Topological mirror superconductivity. Phys Rev Lett 2013; 111: 056403. [DOI] [PubMed] [Google Scholar]
- 33. Chiu CK, Yao H, Ryu S. Classification of topological insulators and superconductors in the presence of reflection symmetry. Phys Rev B 2013; 88: 075142. [Google Scholar]
- 34. Shiozaki K, Sato M. Topology of crystalline insulators and superconductors. Phys Rev B 2014; 90: 165114. [Google Scholar]
- 35. Fang C, Bernevig BA, Gilbert MJ. Topological crystalline superconductors with linearly and projectively represented Cn symmetry. arXiv: 1701.01944.
- 36. Mizushima T, Sato M, Machida K. Symmetry protected topological order and spin susceptibility in superfluid 3He–B. Phys Rev Lett 2012; 109: 165301. [DOI] [PubMed] [Google Scholar]
- 37. Mizushima T, Sato M. Topological phases of quasi-one-dimensional fermionic atoms with a synthetic gauge field. New J Phys 2013; 15: 075010. [Google Scholar]
- 38. Fang C, Gilbert MJ, Bernevig BA. New class of topological superconductors protected by magnetic group symmetries. Phys Rev Lett 2014; 112: 106401. [DOI] [PubMed] [Google Scholar]
- 39. Kopsky V, Litvin D (eds.). International Tables for Crystallography: Subperiodic Groups, Vol. E, 2nd edn. Dordrecht: Kluwer Academic Publishers, 2002. [Google Scholar]
- 40. Tewari S, Sau JD. Topological invariants for spin-orbit coupled superconductor nanowires. Phys Rev Lett 2012; 109: 150408. [DOI] [PubMed] [Google Scholar]
- 41. Samokhin KV. Superconductivity in quantum wires: a symmetry analysis. Ann Phys 2017; 385: 563–83. [Google Scholar]
- 42. Tanaka Y, Yokoyama T, Nagaosa N. Manipulation of the Majorana fermion, Andreev reflection, and Josephson current on topological insulators. Phys Rev Lett 2009; 103: 107002. [DOI] [PubMed] [Google Scholar]
- 43. Alicea J, Oreg Y, Refael Get al. Non-abelian statistics and topological quantum information processing in 1D wire networks. Nat Phys 2011; 7: 412–7. [Google Scholar]
- 44. Feng JJ, Huang Z, Wang Zet al. Hysteresis from nonlinear dynamics of Majorana modes in topological Josephson junctions. Phys Rev B 2018; 98: 134515. [Google Scholar]
- 45. Bernevig BA, Hughes TL. Topological Insulators and Topological Superconductors. Princeton: Princeton University Press, 2013. [Google Scholar]
- 46. Song Z, Fang C, Qi Y. Real-space recipes for general topological crystalline states. arXiv: 1810.11013. [DOI] [PMC free article] [PubMed]
- 47. Yildirim T. Origin of the 150-K anomaly in LaFeAsO: competing antiferromagnetic interactions, frustration, and a structural phase transition. Phys Rev Lett 2008; 101: 057010. [DOI] [PubMed] [Google Scholar]
- 48. Mebrahtu A, Singh P. Coexistence of superconductivity and antiferromagnetism in SmAsO1-xFxFe. World J Condens Matter Phys 2015; 5: 138–47. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


