Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2021 Jun 22;196(3):649–665. doi: 10.1007/s00442-021-04967-y

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2021

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

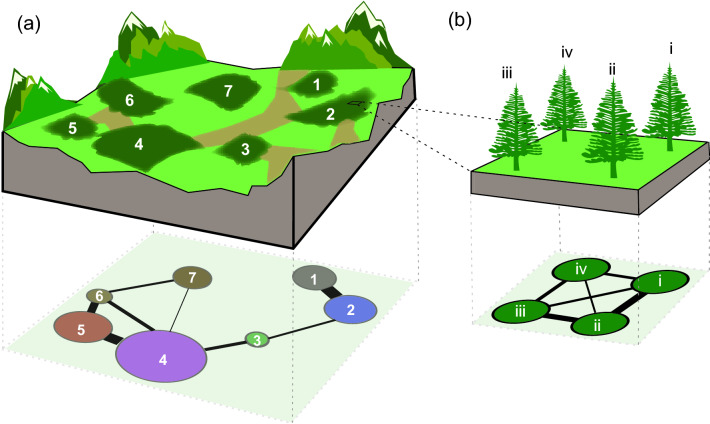
Fig. 2 — Networks explicitly characterizing the physical configurations of animal habitats. We illustrate how five dimensions for assessing habitat configuration proposed by Tokeshi and Arakaki (2012) can be integrated and applied to construct animal habitat networks. These dimensions are (1) spatial scale (spatial resolution and extent), (2) composition diversity (heterogeneity), (3) size (area), (4) abundance or density (number of discrete habitat units per area), and (5) spatial arrangement (distribution) of habitat components. (a) A hypothetical landscape composed by forest fragments (numbered components) within a heterogeneous matrix with potential movement corridors (light green, which account for the presences of links between nodes) and physical barriers (light brown, which account for the absence of links between nodes). The physical features and spatial organization of the habitat components can be represented by a connected network at a large spatial scale, with a high composition diversity (fragments of different tree species), different habitat sizes (small and large fragments), high abundance (7 fragments), and heterogeneous spatial arrangement (fragments unequally distributed and connected by movement corridors across the landscape). (b) The physical features and spatial arrangement of habitat components can be characterized at different spatial scales. Here, part of the forest (fragment 2) can be represented by a connected network at a finer spatial scale (e.g. trees as habitat components), with a low composition diversity (the same tree species), small habitat size (single trees), low abundance of components (4 trees), and uniform spatial arrangement. In the two habitat networks, the compositional diversity (or quality) and size (or carrying capacity) of habitat components are characterized by node attributes (colours and sizes), the abundance by the number of nodes in the networks, and the spatial arrangement by the patterns of connectivity and the distribution of link weights (both as a function of the Euclidean distances between habitat components)