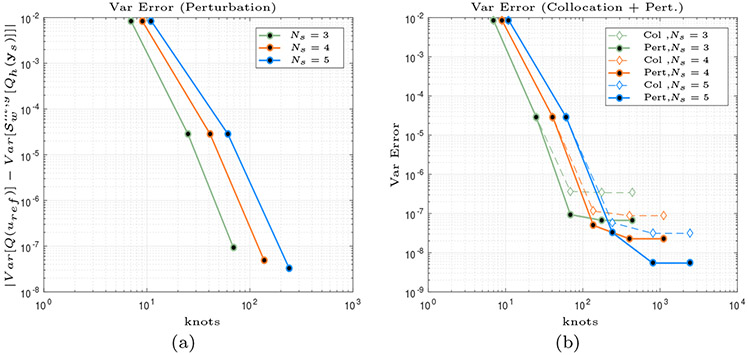
Fig. 5.

Hybrid Collocation-Perturbation results with k = 3 (cubic decay) and c = 1/15. (a) Variance error for the hybrid collocation-perturbation method as a function of the number of collocation samples with a isotropic sparse grid and Clenshaw Curtis abscissas. The maximum level is set to w = 3. (b) Comparison between the pure collocation (Col) and the hybrid collocation-perturbation (Pert) approaches. As we observe the error decays significantly with the addition of the variance correction. However, the graphs saturate once the perturbation/truncation error is reached. Note that the number of knots of the sparse grid are computed up to w = 5 for the pure collocation method. For the variance correction the sparse grid level is set to w = 3 since at this point the error is smaller than the perturbation error and there is no benefit to increasing w. The sparse grid knots needed for the variance correction are almost negligible compared to the pure collocation.