Accelerating Global Tractography Using Parallel Markov Chain Monte Carlo

Abstract

Global tractography estimates brain connectivity by determining the optimal configuration of signal-generating fiber segments that best describes the measured diffusion-weighted data, promising better stability than local greedy methods with respect to imaging noise. However, global tractography is computationally very demanding and requires computation times that are often prohibitive for clinical applications. We present here a reformulation of the global tractography algorithm for fast parallel implementation amendable to acceleration using multi-core CPUs and general-purpose GPUs. Our method is motivated by the key observation that each fiber segment is affected by a limited spatial neighborhood. That is, a fiber segment is influenced only by the fiber segments that are (or can potentially be) connected to its both ends and also by the diffusion-weighted signal in its proximity. This observation makes it possible to parallelize the Markov chain Monte Carlo (MCMC) algorithm used in the global tractography algorithm so that updating of independent fiber segments can be done concurrently. The experiments show that the proposed algorithm can significantly speed up global tractography, while at the same time maintain or improve tractography performance.

1. Introduction

Diffusion magnetic resonance imaging (DMRI) is a key imaging technique for in vivo investigation of white matter pathways in the brain. It probes water diffusion in various directions and at various diffusion scales to characterize micro-structural compartments that are much smaller than the voxel size and presents unique opportunities for non-invasive investigation of white matter connectivity [1–8]. To trace white matter brain connections, local [9–12] or global [13, 14] tractography algorithms can be utilized.

In local algorithms [9, 10], fibers are initiated from a random or predetermined region and are then traced point-by-point using a greedy approach via small successive steps by following local voxel-wise distributions of axonal directions. These algorithms are hence susceptible to error accumulation, which might cause the reconstructed trajectories to deviate from the true trajectories [15]. On the other hand, global tractography (GT) approaches try to reconstruct all fiber trajectories simultaneously by considering their agreement with the underlying diffusion data [13, 14]. They are more resilient to error accumulation and are more robust to imaging noise and artifacts. While effective, the reconstruction of white matter trajectories for the whole brain via GT approaches usually requires much longer time than the local approaches. It was reported in [16, 17] that the computation can take up to one day on a standard PC. This high computational cost reduces the applicability of GT approaches in clinical settings.

Several algorithms were applied to accelerate local deterministic and probabilistic tractography methods via parallelization [18, 19]. They typically spawn an independent thread for each seed voxel so that the tracing of different fiber tracts can be performed in parallel. To the best of our knowledge, there is no existing discussion in the literature about the parallelization of the GT algorithm. In this paper, our goal is to leverage recent advancements in parallel big-data MCMC techniques [20] to improve the speed of the original GT algorithm proposed by Reisert and his colleagues [14], which at its core uses a popular MCMC technique called the Metropolis-Hastings algorithm. As the number of posterior samples grows, MCMC techniques guarantee asymptotically exact recovery of the posterior distribution. However, MCMC methods can be prohibitively slow, since for N data points, most methods must perform $\mathcal{O}(N)$ operations to draw a sample. Furthermore, MCMC methods might require a large number of “burn-in” steps before producing representative samples.

Recently, an embarrassingly parallel approach was proposed in [20] to parallelize burn-in and sampling in MCMC. The key idea is to apply any MCMC method independently to subsets of data without requiring much communication between them. First, the data are partitioned in multiple subsets. Then an MCMC method is used to draw samples from the posterior distribution associated with each data subset. Finally, the samples resulting from all subsets are combined to form samples from the full posterior. This method is termed embarrassingly parallel because the processing of each subset is performed independently without communication with other subsets until the final combination stage.

Building on this concept, we provide a proof of concept in this work that the GT algorithm can be improved significantly in terms of speed by MCMC parallelization. The key observation is that the spatial extent of the influence of each fiber segment is limited. In other words, each fiber segment depends only on the fiber segments that are connected (or can potentially be connected) to its both ends and also on the diffusion-weighted signal that is in its proximity. That is, despite the fact we are trying to decrease the total fitting energy in a global sense, the influence of each fiber segment on the variation of the energy is in fact local. Based on this observation, significant parallelism can be harnessed for improving the speed of the GT algorithm. The data can be partitioned into statistically independent subsets similar to [20] and processed separately before combining the results to form samples for the original problem. Experimental results confirm the effectiveness of the proposed method and demonstrate that similar tractography performance can be achieved in a significantly reduced amount of time.

2. Method

2.1. Background

The goal of GT [14] is to determine the optimal configuration $\mathcal{M}$ of a set of signal-generating fiber segments given the measured diffusion-weighted signals $\mathcal{D}$. That is, one is interested in determining the $\mathcal{M}$ that maximizes the posterior probability $P(\mathcal{M}\mid \mathcal{D})$ defined as

$$P(\mathcal{M}\mid \mathcal{D})=\frac{1}{Z}\text{exp}\left(-E_{\text{int }}(\mathcal{M})-E_{\text{ext }}(\mathcal{M},\mathcal{D})\right),$$ (1)

where $E_{\text{int }}(\mathcal{M})$ and $E_{\text{ext }}(\mathcal{M},\mathcal{D})$ are the internal energy and the external energy, respectively, Z is the partition function. The internal energy characterizes the smoothness of the fibers and is defined as the sum of all the interaction potentials between two connected segments:

$$E_{\text{int}}(\mathcal{M})={\lambda }_{\text{int}}\sum _{\left(e_i^{{\alpha }_{i\to j}},e_j^{{\alpha }_{j\to i}}\right)}\frac{1}{l^2}\left({\Vert e_i^{{\alpha }_{i\to j}}-{\overline{x}}_{ij}\Vert }^2+{\Vert e_j^{{\alpha }_{j\to i}}-{\overline{x}}_{ij}\Vert }^2\right)-L,$$ (2)

where α ∈ {+, −} indicates the positive or negative endpoint of a segment, $e_i^{{\alpha }_{i\to j}}$ is the location of the endpoint of the ith segment that is connected to the jth fiber segment, and ${\overline{x}}_{ij}$ represents the midpoint of the line that connects these two segments. Parameter l is the half length of a fiber segment and the bias L affects the probability of connections between segments. The external energy measures the difference between the observed data $\mathcal{D}$ and the predicted signal given by the configuration $\mathcal{M}$:

$$E_{\text{ext}}(\mathcal{M},\mathcal{D})={\lambda }_{\text{ext}}\Vert F_{\mathcal{M}}-\mathcal{D}\Vert ={\lambda }_{\text{ext}}{\int }_{{\mathfrak{N}}^3\times S^2}{\left|F_{\mathcal{M}}(x,n)-\mathcal{D}(x,n)\right|}^2{d}^{3}x{d}^{2}n$$ (3)

where λ_ext is a weighting for the external energy. Let x_i and n_i be respectively the position and the orientation of ith fiber segment, the signal predicted by the fiber segments at location x and orientation n is defined as

$$F_{\mathcal{M}}(x,n)=w\sum _{i=1}^N\text{exp}\left(-c{\left(n^{\text{T}}{n}_i\right)}^2\right)\text{exp}\left(\frac{-{\left|x-x_i\right|}^2}{{\sigma }^2}\right).$$ (4)

The constant w controls the amount of signal contribution from each fiber segment. Parameter σ > 0 controls the spatial extent of the influence of each fiber segment. Parameter c > 0 controls the shape of the signal profile generated by each fiber segment [14]. The goal of GT is to determine a configuration $\mathcal{M}$ that maximizes the posterior distribution

$$P(\mathcal{M}\mid \mathcal{D})\propto P(\mathcal{D}\mid \mathcal{M})P(\mathcal{M})=\text{exp}\left(\frac{-E(\mathcal{M},\mathcal{D})}{T}\right),$$ (5)

where $E(\mathcal{M},\mathcal{D})=E_{\text{int}}(\mathcal{M})+E_{\text{ext}}(\mathcal{M},\mathcal{D})$ is the total energy and T is the temperature associated with simulated annealing [21].

2.2. Parallel Global Tractography (PGT)

To maximize the posterior probability, an MCMC method called the Metropolis-Hastings (MH) algorithm [22] is employed in [14]. The MH algorithm draws samples from the posterior distribution defined in Eq.(5). However, MCMC methods usually take a long time to draw a sample, proportional to the number of data points [20]. In view of this, we randomly partition the image data into K regions that are mutually non-influential and statistically independent. Then the MH algorithm is applied in parallel by proposing changes to the fiber segments in these regions based on the corresponding transition probabilities. The proposals in these regions are accepted/rejected based on their individual acceptance ratios. The independence condition ensures that the proposals for each of the K regions can be accepted and rejected separately but in parallel. The details are described next.

We first partition the posterior density into subposterior densities [20] based on K randomly determined and statistically independent subregions:

$$P(\mathcal{M}\mid \mathcal{D})=P\left({\mathcal{M}}_0\mid \mathcal{D}\right)\prod _{k=1}^{K}P\left({\mathcal{M}}_k\mid \mathcal{D},{\mathcal{M}}_0\right),$$ (6)

where ${\mathcal{M}}_0$ denotes configuration of the fiber segmentations in the region that separates the K regions to ensure their independence, and ${\mathcal{M}}_k$ denotes the configuration of the fiber segments in the k-th region, including their existence, spatial positions, orientations, and connections at both ends to other fiber segments. Proposals for modification of configuration are made for the fiber segments in each region according to its subposterior density by randomly selecting at each time a fiber segment, perturbing it using a creation/deletion and shifting mechanism, and examining if the regional energy can be decreased. In this process, ${\mathcal{M}}_0$ remains fixed and $\left\{{\mathcal{M}}_k\right\}$ are updated. After $\left\{{\mathcal{M}}_k\right\}$ are sufficiently updated, they are combined to form $\mathcal{M}$. The random partitioning of the image space into subregions is performed iteratively so that each time the fiber configurations of a different set of K random subregions can be updated.

The decision of whether to accept a proposal is based on the individual Green’s ratio of the k-th region

$$R_k=\frac{P\left({\mathcal{M}}_k^{\prime }\mid \mathcal{D},{\mathcal{M}}_0\right)Q\left({\mathcal{M}}_k\mid {\mathcal{M}}_k^{\prime }\right)}{P\left({\mathcal{M}}_k\mid \mathcal{D},{\mathcal{M}}_0\right)Q\left({\mathcal{M}}_k^{\prime }\mid {\mathcal{M}}_k\right)},$$ (7)

where $Q\left({\mathcal{M}}_k^{\prime }\mid {\mathcal{M}}_k\right)$ is the transition probability associated with the MH algorithm. The internal energy contributed by the fiber segments in the k-th region alone is

$$E_{\text{int }}\left({\mathcal{M}}_k\right)={\lambda }_{\text{int }}\sum _{\left(e_i^{{\alpha }_{i\to j}},e_j^{{\alpha }_{j\to i}}\right),i,j\in {\mathcal{N}}_k}\frac{1}{l^2}\left({\Vert e_i^{{\alpha }_{i\to j}}-{\overline{x}}_{ij}\Vert }^2+{\Vert e_j^{{\alpha }_{j\to i}}-{\overline{x}}_{ij}\Vert }^2\right)-L$$ (8)

and the external energy is

$$E_{\text{ext}}\left({\mathcal{M}}_k,\mathcal{D}\right)={\lambda }_{ext}{\int }_{{\mathcal{N}}_k\times S^2}{\left|F_{\mathcal{M}}(x,n)-\mathcal{D}(x,n)\right|}^{2}d{x}^{3}d{n}^2.$$ (9)

where ${\mathcal{N}}_k$ is the index set containing the indices of all fiber segments in the k-th region. The subposterior distribution is

$$P\left({\mathcal{M}}_k\mid \mathcal{D},{\mathcal{M}}_0\right)\propto P\left({\mathcal{M}}_k,{\mathcal{M}}_0\right)P\left(\mathcal{D}\mid {\mathcal{M}}_k,{\mathcal{M}}_0\right).$$ (10)

Note that some proposals are parallelizable and some are not. For each fiber segment, the change in internal energy associated with the creation/deletion and shifting proposals is affected only by the fiber segments it is (or will be) connected to. The change in external energy involves only the diffusion signals in a localized neighborhood surrounding the fiber segment. Hence, the creation/deletion and shifting proposals can be performed independently and simultaneously in different subregions. However, the connection/disconnection proposals, which attempt to determine new fibers with lower energy, involve a larger spatial extent and are hence more difficult to parallelize. To overcome this problem, we alternate between parallel proposals (i.e., creation/deletion and shifting) and serial proposals (i.e., connection/disconnection) according to MH transition probabilities assigned to them. In summary, the PGT algorithm involves repeating the following steps until convergence.

1. Data Partitioning: Randomly partitioning the image space into K subregions, between which the configurations of the fiber segments are not dependent.

2. Parallel Proposals: Make creation/deletion and shifting proposals in parallel for the fiber segments in these regions according to the corresponding transition probabilities and accept/reject the proposals based on their acceptance ratios. Repeat this step for a sufficient number of times.

3. Serial Proposals: Make connection/disconnection proposals and determine fiber tracts that better explain the data.

3. Evaluation

We report here preliminary results from our evaluation of the PGT algorithm using synthetic and in vivo data. The synthetic data consist of a set of 60 × 60 diffusion-weighted images, simulating fiber bundles crossing at 90°. The signal at each voxel was generated using a tensor model or its mixture with principal diffusivities [23] λ₁ = 1.5×10⁻³ mm²/s, λ₂ = λ₃ = 1.0×10⁻³ mm²/s and diffusion weighting b = 2000s/mm². The in vivo dataset for an adult subject was acquired with (2 mm)³ resolution using a Siemens 3T TIM Trio MR scanner. Diffusion gradients were applied in 120 non-collinear directions with diffusion weighting b = 2000 s/mm².

First, we compared the convergence of GT (PGT with one thread) and PGT (eight threads). The parameters used for GT and PGT were set as suggested in [14]. Figure 1 shows the plots of the total energy against the number of proposals for the synthetic and in vivo data. The total energy decreases rapidly at the beginning when less proposals have been made and when the configuration of the fiber segments is more arbitrary. The decrease slows down and flattens when the configuration becomes stable. It can also be observed that PGT is slightly advantageous over GT in its ability to yield lower total energy. This can be attributed to the fact that multiple adjustments of fiber segments are done concurrently, making it easier and faster to reach a configuration with lower energy.

Fig. 1.

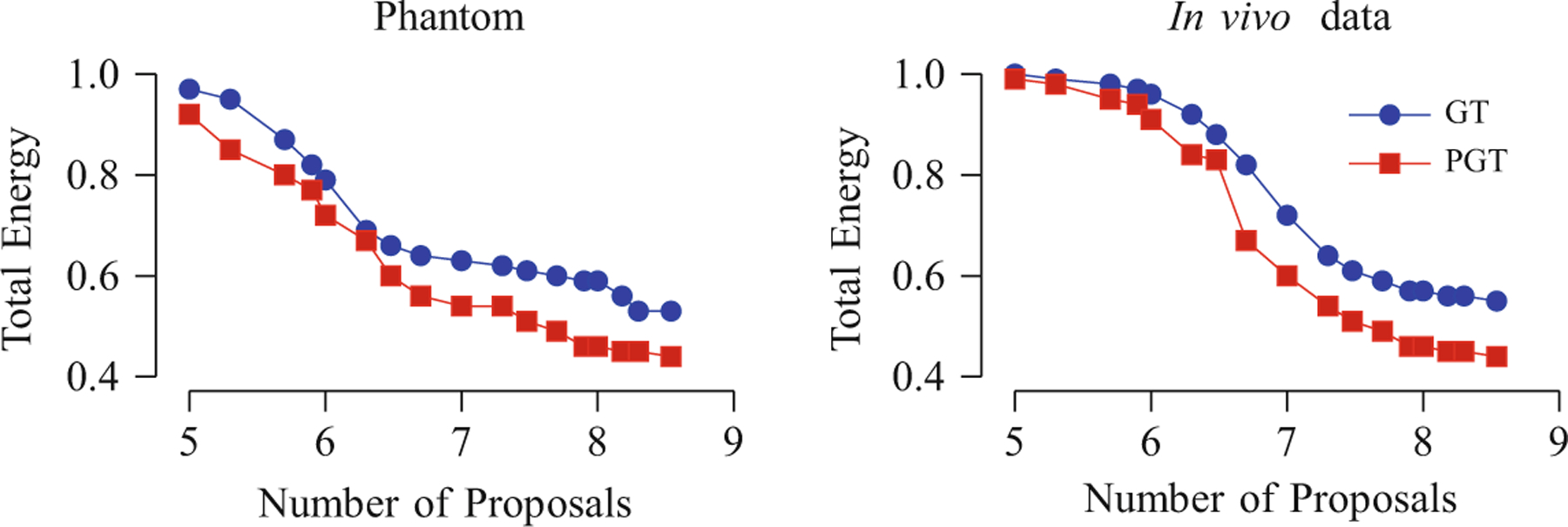
Normalized total energy plotted against the number of proposals (in logarithmic scale)

Next, we evaluated the speed improvement given by PGT over GT. The evaluation was performed using an iMac with Intel 4-Core i7 CPU (3.4GHz each) and 8GB of DDR3 RAM. Figure 2 shows that, on both synthetic and in vivo data, PGT always consumes less than approximately 1=3 the time required by GT. Note that it is not possible to achieve the ideal 8× speed increase because the GT algorithm is only partially parallelized, as discussed in Sect. 2.2. Part of the time also goes to the computational overhead involved in the parallelized implementation.

Fig. 2.

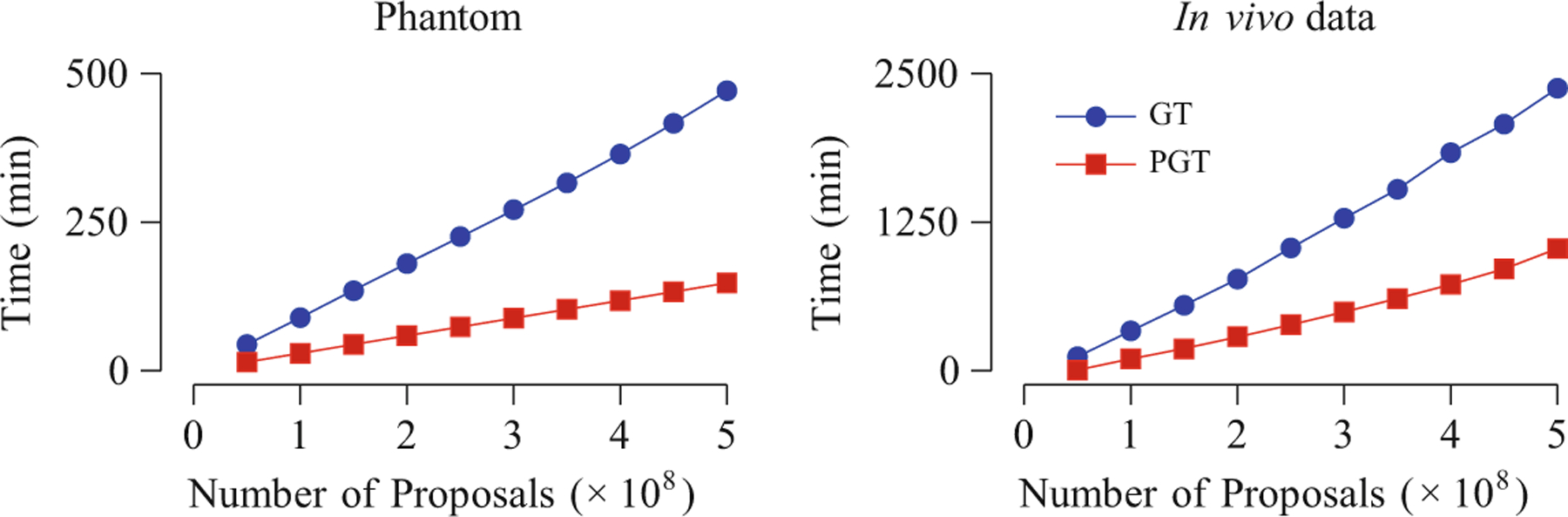
Time costs of GT and PGT

Figure 3 shows the tractography results of GT and PGT on the synthetic data after 2 × 10⁸ proposals. Both GT and PGT create reasonable fiber tracts that are in agreement with the data. The normalized total energy values for GT and PGT are 0.56 and 0.45, respectively. For the in vivo data, fiber bundles extracted with multiple ROIs [24] are shown in Fig. 4. These fiber bundles are similar to those in [14]: the part of the callosal fibers coming from the left motor cortex (CCtoM1), corticospinal tracts to the left motor cortex (CST), and the cingulum (CG). These are shown from top to bottom in the figure. PGT results in fiber bundles that are similar to GT, but in a fraction of time.

Fig. 3.

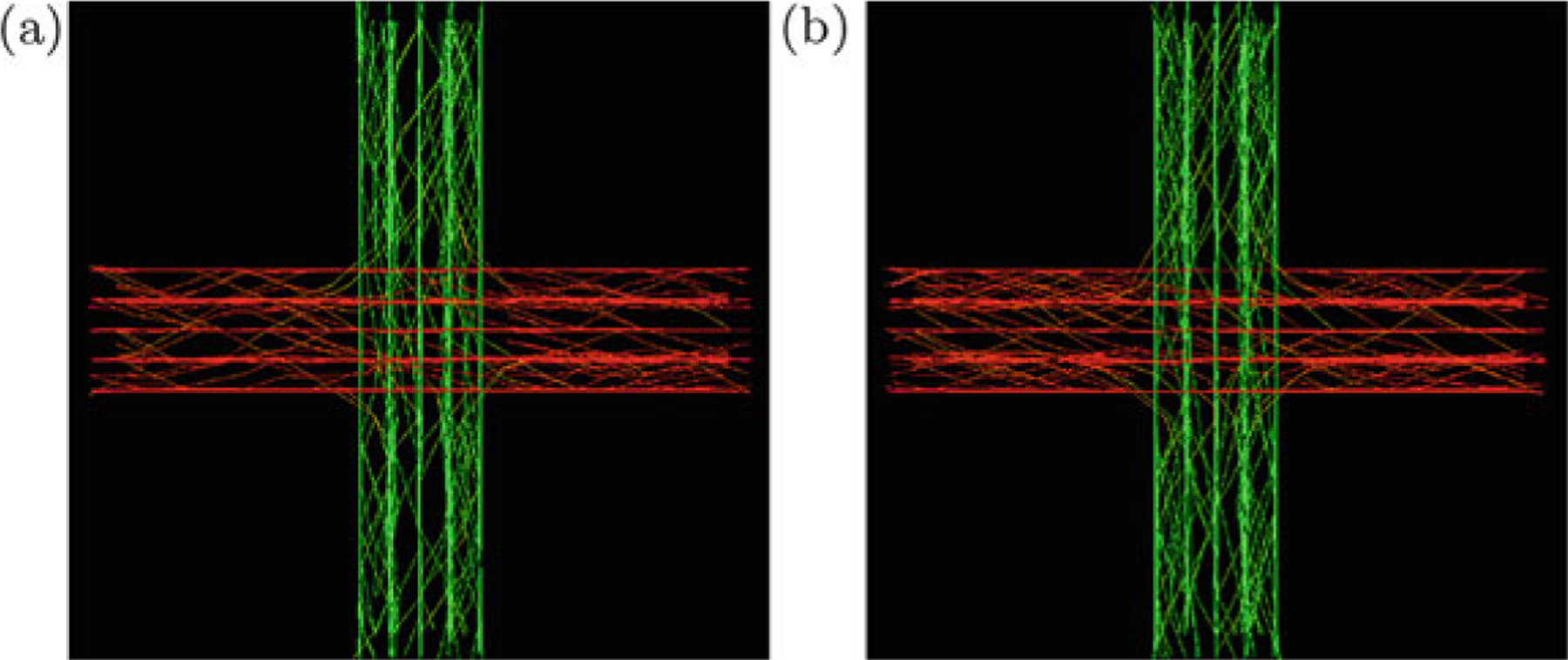
Tractography results on synthetic data using (a) GT and (b) PGT

Fig. 4.

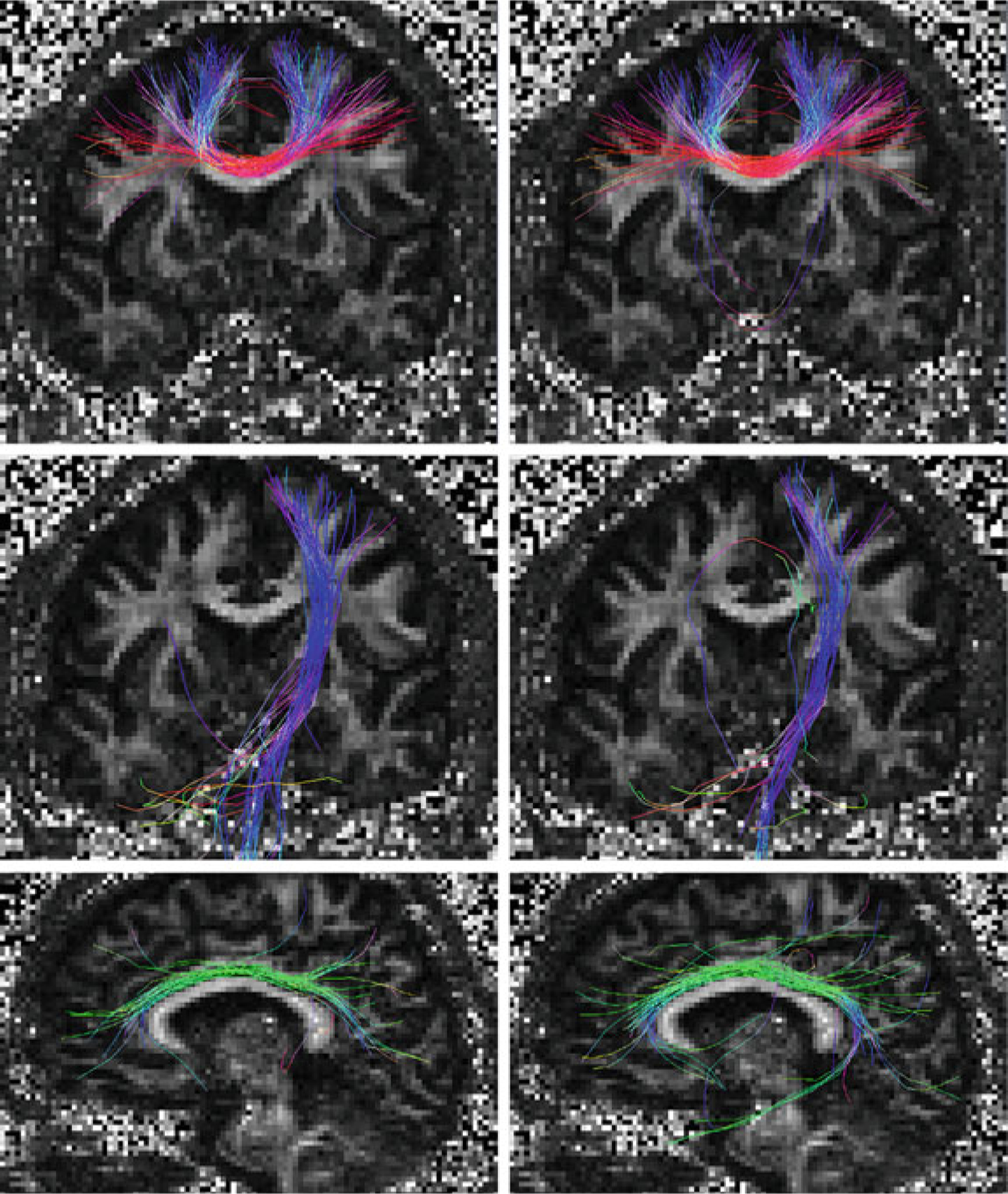
Fiber bundles given by GT (left) and PGT (right)

4. Discussion and Future Work

The proposed algorithm helps to reduce the time cost associated with the global optimization process required in global tractography. We run in parallel multiple independent chains of MCMC on a number of dynamically determined subregions, resulting in faster convergence and producing results that are comparable to the non-parallelized version. Future implementation based on GPUs will further improve the speed of global tractography and hence its feasibility in large-scale studies.