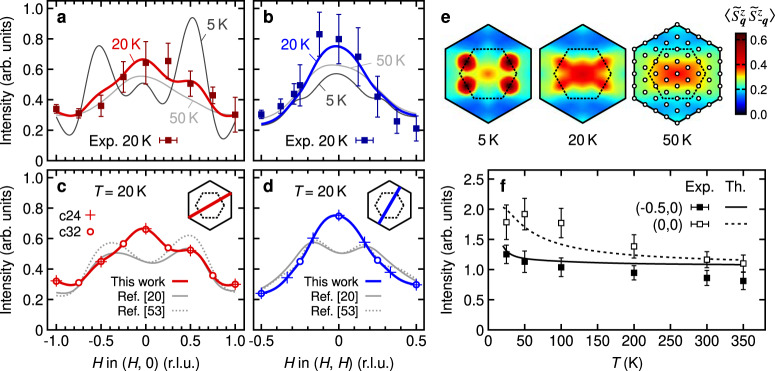
Fig. 5. Theoretical RIXS intensity and pseudospin correlations in the Kitaev–Heisenberg model.

a, b Momentum dependence of the theoretical RIXS intensity calculated at T = 5 K (dashed), 20 K (solid blue), and 50 K (solid cyan), using the pseudospin Hamiltonian [Eq. (1)]. To obtain the best fit to the experimental data (squares), the exchange parameters K = −5, J = −3, Γ = 2.5, ${\mathrm{\Gamma }}^{\prime }=0.1$ and J₃ = 0.75 meV were used. c, d Comparison of the RIXS intensity computed with different parameter sets. The optimal theoretical curve is compared with those for the parameter sets proposed in refs. ²⁰ and ⁵³. The insets show the q paths. The points represent results at the accessible q vectors for the 24-site cluster (crosses) and 32-site cluster (circles) that were used to construct the smooth profiles. e Temperature evolution of the equal-time pseudospin correlation function $⟨{\tilde{S}}_{\mathit{q}}^z{\tilde{S}}_{-\mathit{q}}^z⟩$ for the optimal parameter set. The maps were calculated for the 32-site cluster with the accessible q vectors (circles) marked on the 50 K map. f Temperature dependence of the RIXS intensity at q = (0, 0) and (−0.5, 0). The data points were collected with the azimuthal angle of ϕ = 0 [the geometry for the (H, 0) path]. The lines show the theoretical curves obtained by a simulation for the 24-site cluster.