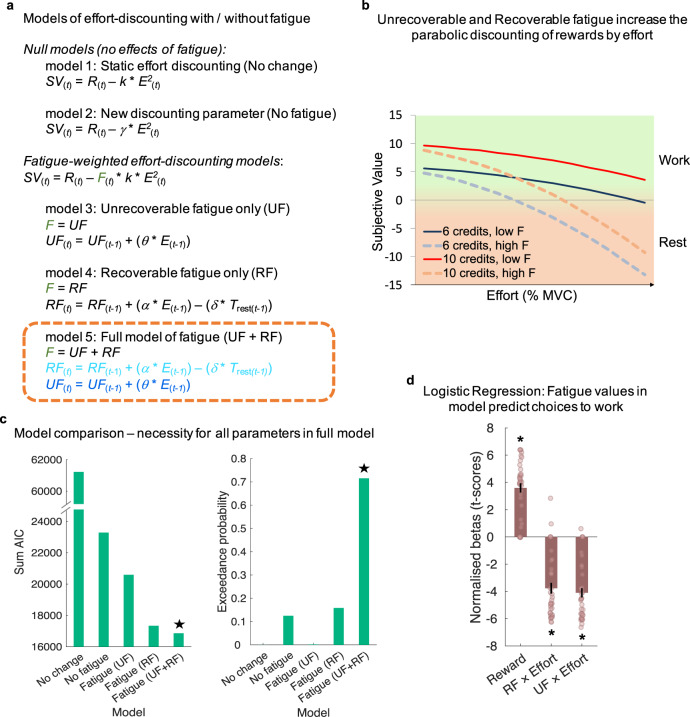
Fig. 3. Modelling the fatigue-weighted subjective value of effort and reward.

a List of main models compared. All models assume that rewards (R) increase subjective value (SV), effort (E) decreases SV, and people discount the rewards by effort idiosyncratically—modelled with a discount parameter (k) fitted to the pre-task. Two null models assume that the willingness to exert effort for reward remains static across the trials of the main task, either with the same discounting parameter as for the pre-task (k; model 1) or with a new discounting parameter ($\gamma$; model 2). Models 3–5 capture changes in effort discounting due to fatigue. The full model (model 5) assumes that exerting effort increases recoverable fatigue (RF), but time (T_rest) spent resting decreases it. Both of these are scaled for each participant by two corresponding free parameters that define a person’s short-term fatigability ($\alpha$, $\delta$). Unrecoverable fatigue also increases through exerted efforts, but never declines. This is also weighted by an idiosyncratic free parameter ($\theta$), which defines long-term fatigability. These are summed to create F, which then serves to increase the discounting of rewards by effort as they increase. Models 3 and 4 include only the effects of UF or RF. b Schematic representation for how F (both UF and RF combined) affect value and choices to work or rest, with greater discounting of rewards by effort as fatigue increases. c Model comparison highlights that the full model is a better predictor of choice data than the simpler models in terms of AIC (left) and in exceedance probabilities (right), highlighting that both RF and UF are necessary to understand the willingness to exert effort. Star indicates winning model. d Furthermore, the model-estimated RF and UF—from model 5—significantly interacted with effort to predict choice behaviour in a logistic regression. The asterisks show significant t-scores (two-tailed p < 0.001) and the error bars represent SEM; n = 36.