Table 2.

Partial Differential Equations for the Relative Error, 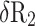, for in the Calculation of Corneal Back Surface Radius

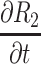	[2(t - B - √C)V - 2U]/V2
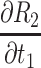	[4(K1t1) + 2t1 −2h1K1 + {2K2(t1+K1t1)/√[t12+(K1t1)2]}]/V – U{2t1(1+K1)/ √[t12+(K1t1)2]}/ V2
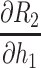	h1(2+2K52+4K5)+[2K8(K6+K7)]/V – U(K6 + 2K7)/V2
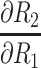	2{V[K11 - K12 + ([B-t+ √C]x[1- K9 –K10])] – U[1 - K9 -(h12t12/R13√C)]}/V2

Notes: Where, with reference to Figure 1, h₁= distance from the apex of the cornea and a peripheral location on corneal surface, t₁= the length of the perpendicular stretching from this peripheral location on the corneal front surface to the peripheral corneal surface (ie, the thickness of the cornea at this peripheral location); t = thickness at the apex of the cornea; R₁ = corneal front surface radius, and A = h₁ - (h₁t₁/R₁); B= R₁ - √(R₁² – h₁²); C= t₁² + (h₁t₁/R₁)²; U= A² + (B + √C – t)²; V= 2(B + √C - t); K₁= h₁/R₁; K₂= B-t; K₃=K₁+1; K₄= h₁t₁; K₅= t₁/R₁; K₆= h₁/√(R₁² - h₁²); K₇ = h₁K₅²/√(t₁² + [h₁K₅]²); K₈ = B + √(t₁² + [h₁K₅]²; K₉ = R₁/√(R₁² - h₁²); K₁₀ = h₁²t₁²/R₁³√C]; K₁₁= h₁²t₁/R₁²; K₁₂= h₁²t₁²/R₁³.