Insights into the Binding of Intrinsically Disordered Proteins from Molecular Dynamics Simulation

Abstract

Intrinsically disordered proteins (IDPs) are a class of protein that, in the native state, possess no well-defined secondary or tertiary structure, existing instead as dynamic ensembles of conformations. They are biologically important, with approximately 20% of all eukaryotic proteins disordered, and found at the heart of many biochemical networks. To fulfil their biological roles, many IDPs need to bind to proteins and/or nucleic acids. And while unstructured in solution, IDPs typically fold into a well-defined three-dimensional structure upon interaction with a binding partner. The flexibility and structural diversity inherent to IDPs makes this coupled folding and binding difficult to study at atomic resolution by experiment alone, and computer simulation currently offers perhaps the best opportunity to understand this process. But simulation of coupled folding and binding is itself extremely challenging; these molecules are large and highly flexible, and their binding partners, such as DNA or cyclins, are also often large. Therefore, their study requires either or both simplified representations and advanced enhanced sampling schemes. It is not always clear that existing simulation techniques, optimized for studying folded proteins, are well-suited to IDPs. In this article, we examine the progress that has been made in the study of coupled folding and binding using molecular dynamics simulation. We summarise what has been learnt, and examine the state of the art in terms of both methodologies and models. We also consider the lessons to be learnt from advances in other areas of simulation and highlight the issues that remain of be addressed.

Graphical Abstract

Introduction

Over the last twenty years, the traditional structure-function paradigm has undergone a fundamental re-evaluation. While we have long been taught that proteins rely on their three dimensional structure for their biological function, we now know that this is not necessarily the case. Intrinsically disordered proteins (IDPs) are a class of protein that are natively unfolded.^1,2,3,4,5 When unbound and in solution, they do not possess a single well-defined secondary or tertiary structure. They exist instead as dynamic ensembles of conformations that may be largely unstructured but possessing transient residual structure, consist of multiple structured states that rapidly interchange, or something in between.^6,7,8,9 IDPs are also recognized to play important functional roles in biology:¹⁰ a survey of 194 eukaryotic proteomes revealed that 15–25% of proteins in multicellar eukaryotes (and up to 36% in unicellular eukaryotes) are disordered,¹¹ and evolution is known to specifically conserve protein disorder.¹²

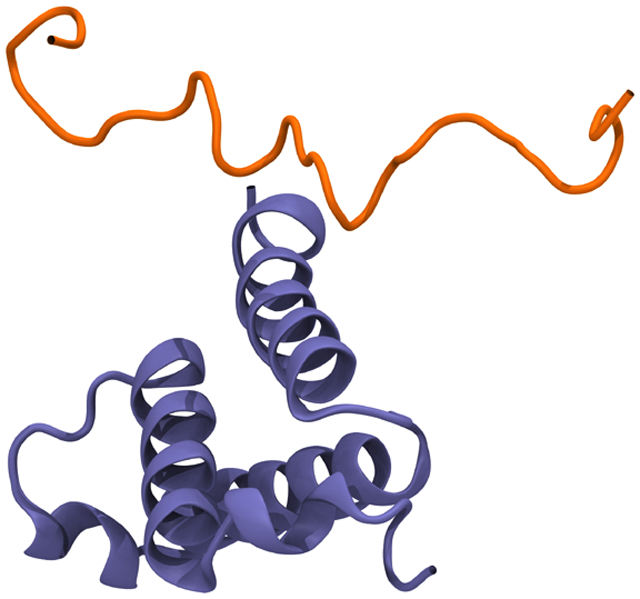
Intimately associated with the biological function of IDPs is the process of coupled folding and binding.^13,14 While IDPs are unstructured in solution, they typically (though not always^15,16,17) fold into a well-defined three-dimensional structure upon interaction with a binding partner. The binding partner can be another IDP,^18,19 a globular protein¹³ or a nucleic acid,^20,21 but the result is a well-ordered complex in which the IDP usually adopts a well-defined secondary structure, and is said to have undergone coupled folding and binding (Figure 1). With ~20% of the proteome consisting of disordered proteins, these coupled folding and binding events are biologically common. In particular, they are “at the heart of many signaling and regulatory cascades”.²² Since coupled folding and binding is at the heart of many biological networks, it is also strongly associated with diseases including cancer, cardiovascular disease, amyloidosis, nueurodegenerative disease and diabetes.^23,24,25

Figure 1.

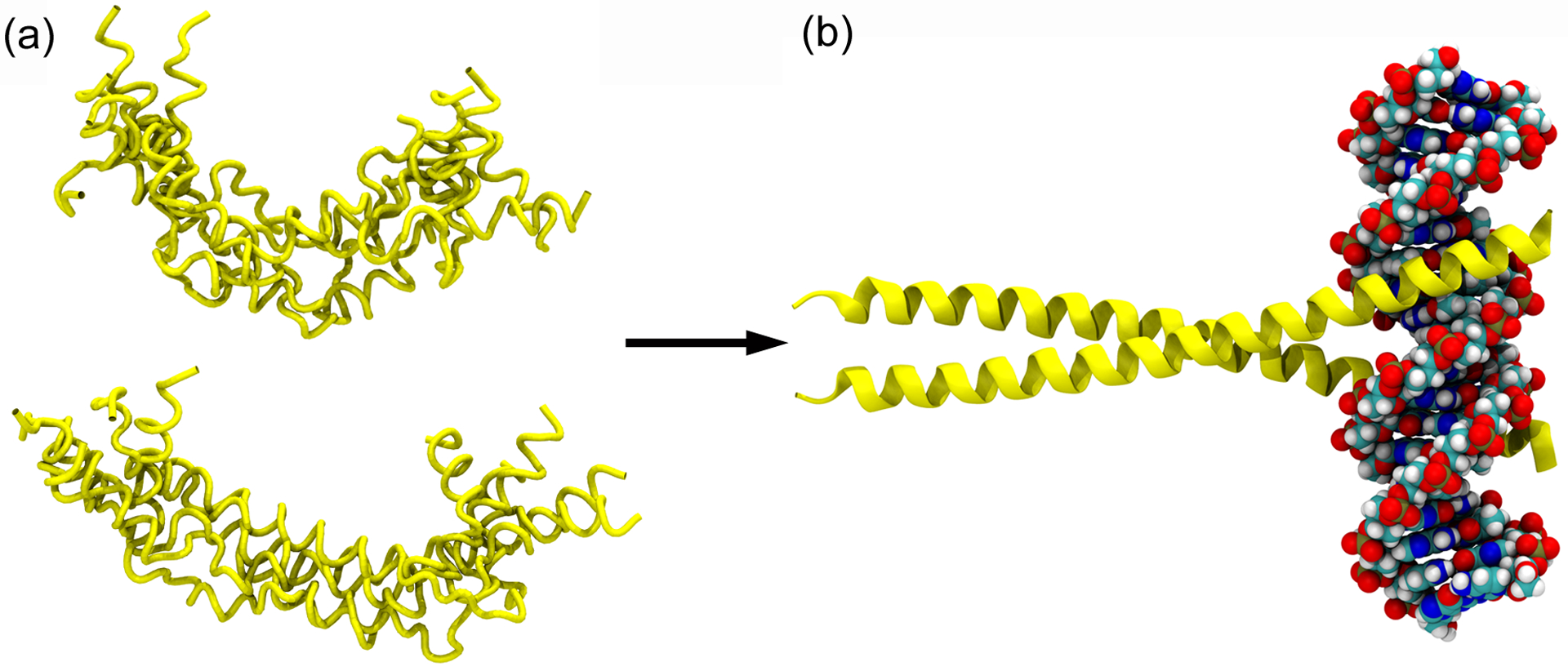
The protein Jun is an IDP that undergoes coupled folding and binding to form homo- or hetero- dimeric complexes with DNA.¹⁷² (a) Two jun monomers, each shown as an ensemble of five conformations taken every 200 ns from a 1 μs Gō model simulation of the isolated protein. (b) The crystal structure of the Jun-Jun homodimer in complex with DNA, from PDB 2H7H.¹⁷³

Understanding the Function of Intrinsic Disorder

Coupled folding and binding is so widely employed in biology that it must confer some kind of functional advantage. But the exact reasons why biology employs this mechanism remain unclear, though a number of possible explanations have been proposed. For an IDP, the favourable contact free energy upon binding is offset by the loss of configurational entropy associated with folding, resulting in complexes that can be highly specific but have a low overall binding free energy (affinity).²⁶ It has also been suggested that the conformational plasticity of IDPs allows them to achieve excellent complementarity with the binding surface of their binding partner,²² and it has been observed that IDPs can adopt a variety of different conformations to interact with multiple different binding partners.²⁷ In DNA binding proteins, where disordered regions are common,²⁸ it has been suggested that they help the protein to search the DNA sequence by increasing the affinity of the protein for the DNA²⁹ and encouraging ‘sliding’.³⁰ And in the same DNA binding proteins, disordered regions are believed to facilitate intersegment transfer – the movement between different DNA chains – via a so-called ‘monkey bar’ mechanism, in which the disordered region forms a bridge from one strand to another, allowing the rest of the protein to then jump between the strands.^30,31 It has also been noted that IDPs form binding surfaces that are very large in comparison to the number of residues they possess, and that a globular protein would need to be much larger to form a binding interface of comparable size.³² In addition to these advantages accessible to IDPs, the ‘fly-casting’ mechanism³³ holds that IDPs possess a kinetic advantage for binding that arises from their extended structures. In these extended structures, IDPs have a large capture radius, meaning that they can make initial contact with their binding partners at large separations, reducing the three-dimensional search space. The mechanism suggests that the IDPs subsequently fold as they are ‘reeled in’ towards their partners. The disordered state of IDPs may also allow them to take advantage of non-specific interactions which keep them in the vicinity of their binding partner, thus enhancing their binding rate.³⁴

While these explanations help us to understand the biological role of coupled folding and binding, the molecular mechanism of binding remains unclear. One of the most active debates in the field, for example, is whether coupled folding and binding occurs via ‘conformational selection’ or ‘induced fit’³⁵ (Figure 2). The induced fit mechanism says that an IDP binds to its partner in an unfolded state, subsequently folding (while bound) to form the well-structured complex. The conformational selection mechanism says that an IDP exists as a fluctuating dynamic equilibrium of conformations, some of which will correspond to the conformation in the bound state; these will be selected for binding by the partner molecule. This then also raises the question: if not conformational selection, what is the role (if any) of the transient secondary structure formed in the disordered ensemble?^36,37

Figure 2.

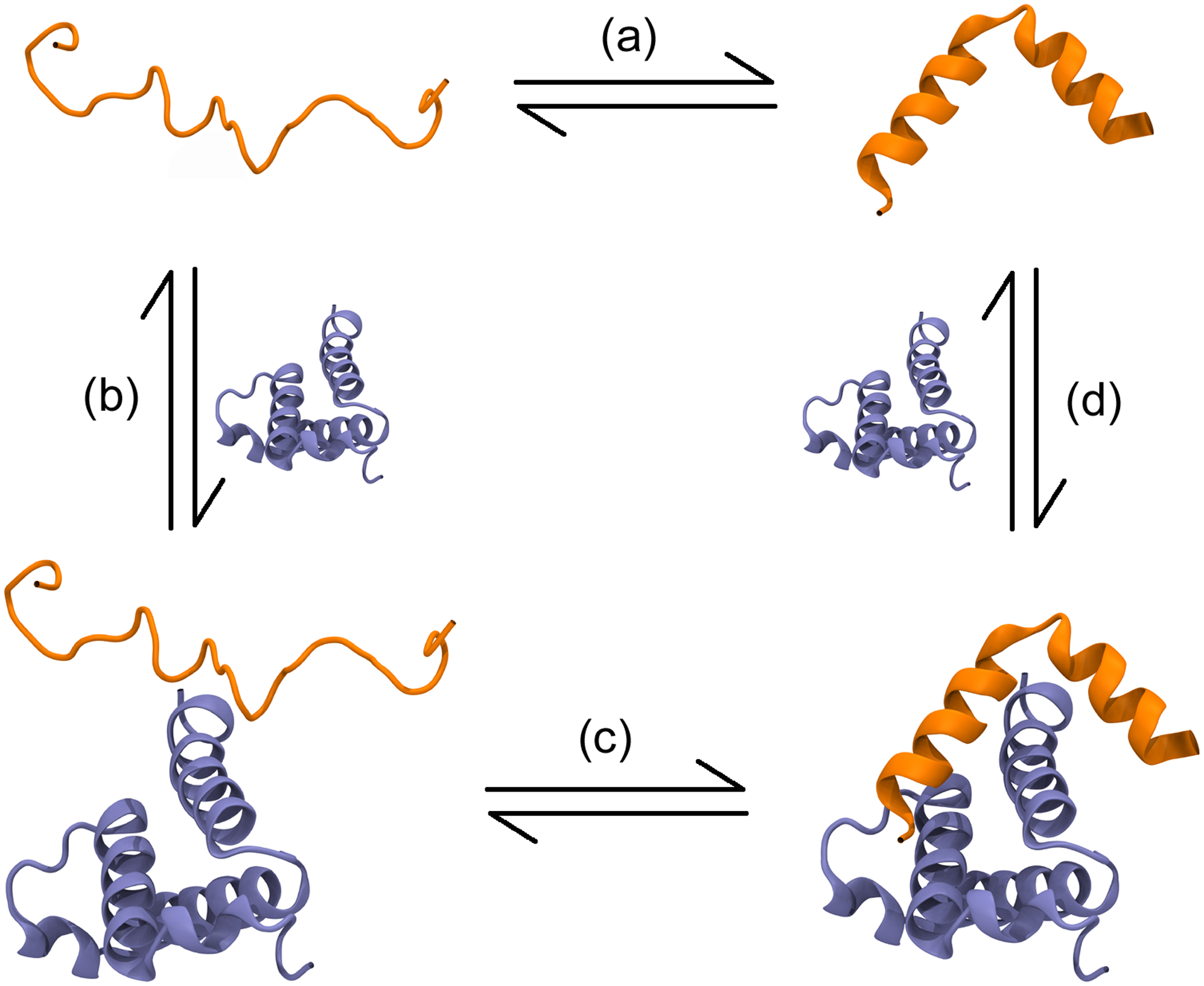
Possible mechanisms for coupled folding and binding, illustrated using the proteins pKID and KIX. (a) When unbound, an IDP exists as an equilibrium between multiple distinct structures, which may include the fully folded structure. (b) According to the induced fit folding mechanism, the IDP binds to its partner in the unfolded state before (c) folding while attached to its partner. (d) The conformation selection mechanism suggests that the partner protein selects folded structures from the equilibrium ensemble of the IDP, and binds only to them.

Experimental Information on IDP Ensembles

One reason that we do not have a complete understanding of coupled folding and binding is that it is difficult to study experimentally. Bound and folded states with well defined secondary and tertiary structures can be characterized using standard methods of protein structure determination. However in the unbound state, IDPs exist as dynamic ensembles of conformations, making it extremely difficult to characterize their structures: the size of the disordered ensembles is so vast that they cannot be uniquely determined from ensemble-averaged experimental data.^26,38 Single molecule experiments, most notably FRET, can in principle overcome the problem of ensemble averaging, but yield relatively coarse structural information (i.e. the distance between a pair of residues). However, while FRET may not yet have the time resolution needed to resolve directly the fast fluctuations in distance in the unbound state, it can nonetheless probe those time scales by using photon correlation functions.³⁹ Of the ensemble experimental methods which are applicable to IDP ensembles, nuclear magnetic resonance (NMR) spectroscopy is a very rich source of information, although typically with low time resolution; its application to IDPs has been recently reviewed.⁴⁰ It can provide both local probes of structure such as scalar couplings (reporting on torsion angles), short-range NOE’s (reporting on local turn or helix formation), and chemical shifts which can be related mainly to local structure via empirical shift prediction algorithms such as SPARTA+⁴¹ or Camshift.⁴² Residual dipolar couplings, which provide information on relative bond orientations, can be a source of both local and long-range structural information – however, their interpretation in the case of IDPs is relatively complex, due to the need to predict the alignment tensor. A very useful source of long-range structural restraints is NMR paramagnetic relaxation enhancement (PRE) data: in recent work, Monte-Carlo based structure calculations were used to obtain high-resolution inter-residue contact maps describing transient tertiary contacts in disordered states of proteins, consistent with PRE data.⁴³ While each NMR method provides only restricted information, the accumulation of a sufficiently large amount of NMR data on disordered peptides can, in principle, be used to derive information on structure and dynamics.⁴⁴ A second major source of structural information for IDPs is small-angle X-ray scattering (SAXS), whose application to IDPs has also been recently reviewed.⁴⁵ SAXS primarily provides information on long-range structural correlations, and is most powerful in combination with methods such as NMR which provide complementary short-range information; indeed, there is an increasing trend towards a global analysis of different types of experimental data, either to determine ensembles using restraints, or as a means to validate ensembles.³⁷

Studying the mechanism of binding experimentally is also challenging. NMR relaxation-dispersion experiments can be used to determine structural details of intermediate states on the folding/binding pathway, though are limited by a requirement for slow exchange and practical restriction on the description of processes with many intermediate states.²⁶ Kinetic measurements can however lead to important insights, such as whether or not the binding is limited by translational diffusion or barrier crossing.⁴⁶ Alternatively, measuring changes in kinetics and stability upon binding can be used to obtain residue-specific information on mechanism.⁴⁷ The interpretation of this information is not unambiguous, however.

A Role for Simulation

One technique that could be used to overcome these problems, and that has the potential to provide an explicit atomic-level description of coupled folding and binding, is molecular simulation, but simulating these systems also presents significant challenges.

The first major challenge is that of simulation time. Coupled folding and binding occurs on the microsecond-millisecond timescale, similar to protein folding. In recent years, enormous effort has been expended on simulating protein folding at atomic resolution in explicit solvent, and significant progress has been achieved.⁴⁸ However, long timescale equilibrium simulations that sample multiple folding and unfolding events are still limited to researchers working with extremely powerful bespoke computer hardware.^49,50,51 For the simulation of coupled folding and binding, the problem is even more challenging because the system size cannot be reduced to the extent that it can in protein folding, purely because coupled folding and binding requires the presence of at least two biomolecules. With this in mind, we are probably forced to conclude that, for the average researcher, long timescale equilibrium simulations of coupled folding and binding at atomistic resolution are not currently a realistic possibility. But this need not be the end of the story. Work on protein folding has shown us that there is much important information that can be obtained using simplified models, enhanced sampling techniques and careful design of simulation systems.⁴⁸

The second major challenge to the simulation of coupled folding and binding has the potential to be even more serious, and concerns the accuracy of the potential functions used in simulations. Again, experiences from protein folding are instructive. When the simulation of protein folding at atomic resolution in explicit solvent first became possible, it was quickly apparent that the results obtained were not in agreement with experimental data. In particular, many all-atom force fields favoured formation of either the α-helical or β-sheet structure,^{48,52,53,54,55,56} meaning that researchers were required to choose their force field based on the secondary structure of the protein that they were trying to fold. This situation inspired the re-optimization of parameters for several force fields until the correct balance between different secondary structures could be achieved,^57,58,59 and more recent results are much improved.^50,60,61 At the same time, however, the details of the folding mechanism are still dependent on the force field used,⁵⁹ and there is a tendency to predict the folded states of proteins to be more compact than experiment suggests.⁶² By extension, one might also expect that current force fields will predict protein complexes to be too ‘compact’: that they will overestimate their stability. Observed deficiencies in the representation of weakly-structured proteins have also led to re-optimization of parameters for several force fields,^63,64,65 providing a more accurate representation of the unfolded states of IDPs.⁶⁶ But the optimization of classical force fields for the simulation of IDPs still presents some unique challenges. As discussed above, the data that can be obtained from experiments is often limited, while an IDP can only be described by an ensemble of structures. This means that there is often not enough information to unambiguously determine the optimum set of force field parameters: several different sets of parameters may give structural ensembles that are all slightly different, but that all reproduce the available experimental data. How exactly to resolve this issue remains unclear, though it can be reduced by maximising the amount of experimental data considered, and targeting multiple ordered and disordered proteins during the parameter optimization. Due to the large size and complexity of the systems in question, atomistic simulation of coupled folding and binding under equilibrium conditions has not yet been achieved, and this means that a critical assessment of the ability of existing force fields to reproduce the details of this process is not possible. We can surmise that the work performed to optimize force fields for protein folding and simulation of weakly structured proteins should have resulted in force fields that provide a good representation of IDPs and their folding, but we cannot be certain that these force fields will be able to accurately capture the perturbation introduced by the presence of the binding partner. And we will also need to consider molecules that are not proteins. In the nucleic acids, for example, force field parameters have again been under constant revision to provide the best possible fit to experimental data,^67,68,69 but never tested in the context of coupled folding and binding. Overall, if the case of protein folding has taught us one thing, is that all-atom simulations of coupled folding and binding will provide a very stringent test of the quality of existing force fields, and may provide insights into the nature of any inaccuracies.

Where are we now?

Gō model simulations

One approach that allows us to circumvent the problems described above is the use of topology-based Gō models.⁷⁰ Gō models are coarse-grained⁷¹ representations, most typically with a single interaction site per residue, located at the Cα position (Figure 3). The small number of particles included in the model means that simulations are much faster than equivalent all-atom simulations, with speeds of the order of 1 μs per day achievable on a single core. In a Gō model, the non-bonded interaction terms are based on the native topology of the system being studied. Specifically, a short-range attractive pair potential is used to describe interactions between residues that are in contact in the folded state. All interactions between residues that are not in contact in the native state are then described using an excluded-volume repulsion term.⁷²

Figure 3.

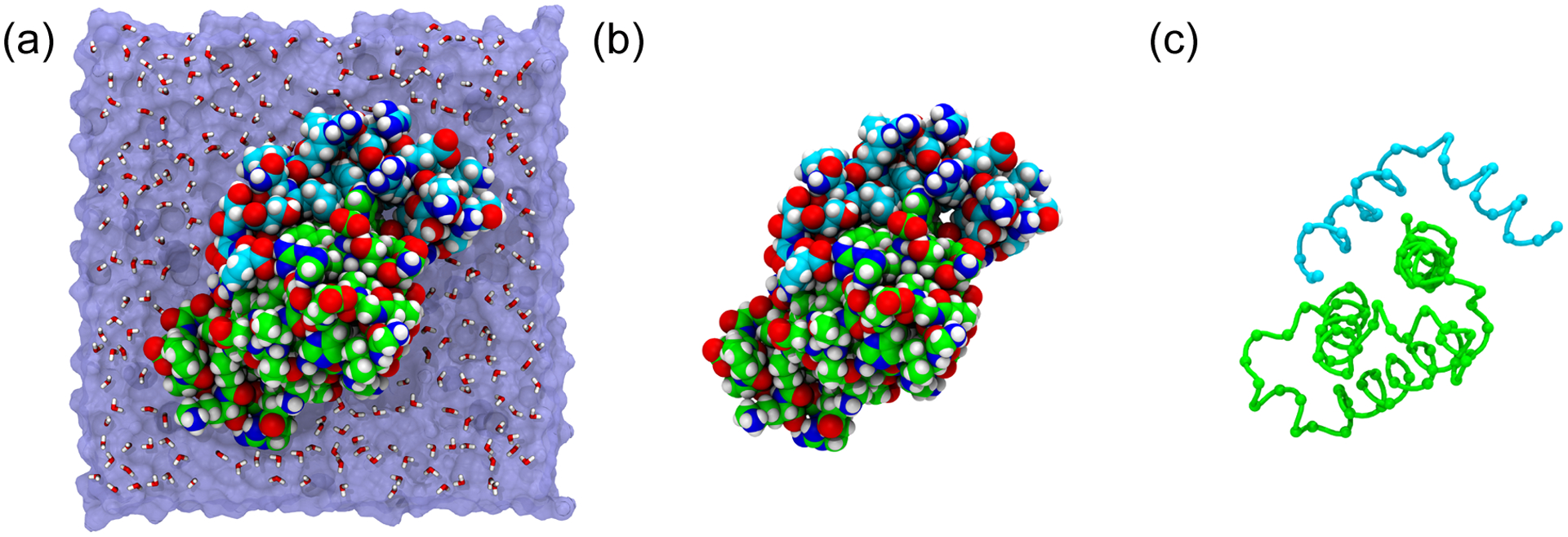
Different scales of representation for molecular dynamics simulations of the pKID-KIX system. (a) All-atom model with explicit water. (b) All-atom model with implicit water. (c) Coarse-grained Cα model.

Gō models have been widely applied in the study of protein folding, where they have been remarkably successful.^73,74 Including only native interactions, Gō models describe the folding energy surface as smooth and funnel-like. Their success, therefore, has been interpreted as a validation of energy landscape theory,^75,76,77 which is based on the hypothesis that protein sequences have evolved to minimize the influence of non-native interactions on folding such that their energy landscapes are smooth and possess a “funnel–like” bias toward the native state, allowing them to fold on biological timescales.⁷²

Levy et al.⁷⁸ extended Gō model simulation to the study of protein binding, simulating¹¹ different peptide sequences known to form homodimers. A variety of different binding mechanisms were observed, including coupled folding and binding, but the authors’ most important conclusion was “that the binding mechanism is robust and is governed by protein topology.” In short, that Gō models are as appropriate for studying protein:protein binding as they are for studying protein folding. Several groups have since employed Gō models to study coupled folding and binding. Wang et al.⁷⁹ studied the complex between the proteins Cdc42 and CBD. By monitoring Q, the fraction of native contacts, they showed that CBD is unstable in isolation, but folds during binding to Cdc42. They also identified a number of residues that act as nucleation points in the folding/binding pathway and explained the mechanism by which this process occurs, finding that “folding and binding do not proceed independently (individually) but are intimately coupled. It is more likely that the whole binding process progresses first as the partial folding of CBD to very limited amount (only 20%, mostly through local folding), then as significant interface binding (70%, without much further folding), and finally as binding and folding cooperatively to the native state.” The same authors subsequently performed single molecule fluorescence experiments that lent further support to the conclusions drawn from their simulations.⁸⁰

Ganguly et al.⁸¹ took the Gō model approach a step further by using it to simulate the synergistic coupled folding and binding of two IDPs, NCBD and ACTR. Their main interest was in evaluating the mechanism by which coupled folding and binding occurs, and they ultimately concluded that it was somewhere between induced fit and conformational selection, though slightly closer to induced fit. In fact, the conclusions from these two studies are in line with what is becoming the generally accepted view: that neither conformational selection nor induced fit provides a perfect description of the mechanism by which coupled folding and binding occurs. Csermely et al.⁸² have argued that these two models actually represent the limiting cases in what they term the “extended conformational selection” mechanism. According to this view, binding occurs via a series of steps – initially, the binding partner selects conformations of the IDP that are appropriate for binding. This is then followed by a structural rearrangement of the resulting complex (i.e. an induced fit), which gives rise to a new structure with its own ensemble of conformations. The most appropriate conformations for further binding are selected from this ensemble, followed by additional rearrangements and so on until the fully bound/folded structure is formed. Further support for this mechanism comes from work on ubiquitin binding, where studies considering both experimental⁸³ and simulation⁸⁴ data have concluded that an initial conformational selection is followed by induced fit in the binding site. Naganathan and Orozco also studied NCBD with a hierarchy of models, ranging from an analytically solvable Ising-like phenomenological model, to an off-lattice Gō model and finally atomistic simulations, finding that the protein has many characteristics of a “downhill folder”, namely a protein for which there is no free energy barrier to the formation of folded structure.⁸⁵ From their models, the authors also predicted the presence of a minor conformation with a population of ~8%: subsequent NMR experiments confirmed the existence of this conformation, and found it to have a population of 8%.⁸⁶ This result highlights the potential value of using a range of different models, where the different time and length scales considered allow for the direct inclusion of/comparison to a wider range of experimental data than would otherwise be possible.

Probably the mostly widely simulated coupled folding and binding is that between the phosphorylated kinase inducible domain (pKID) of CREB, an IDP, and the natively structured KIX domain of the co-activator CBP (Figure 3).^87,88 Turjanski et al.⁸⁹ used Gō model simulations to identify that binding occurs prior to folding, in agreement with NMR experiments published simultaneously,⁸⁸ and used φ value^90,91 analysis to identify a leucine residue important to the process. This study also found that, if pKID was given additional structure, then binding occurred more slowly, in accord with the fly-casting mechanism. Huang and Liu,⁹² however, used Gō model simulations of pKID-KIX to question whether the fly casting mechanism really does explain the kinetic advantage enjoyed by IDPs. In their simulations, intrachain interactions in pKID were made progressively stronger, resulting in a transition from disordered to ordered protein, with binding to KIX studied in each case. They concluded that while IDPs do have a larger capture radius, they also have a larger hydrodynamic radius and therefore diffuse more slowly, resulting in a capture rate that is similar to that obtained for a natively structured protein. An important caveat to this work, however, is that (like most Gō models) it did not include long-range interactions; furthermore, the effect of the change in temperature on the diffusion coefficient was not considered. IDPs are known to contain more charged residues than natively folded proteins,² and electrostatic interactions would be expected to increase diffusion rates via a long-range attractive potential. Indeed, Levy et al.⁹³ included a Coulombic attraction term in a Gō model simulation of the coupled folding and binding between Ets-1 and DNA and found that the initial unspecific binding was driven by electrostatics, and that the higher the charge on the two molecules, the faster they came together. Using a similar approach to study the p27-cyclin A complex, Ganguly et al.⁹⁴ concluded that electrostatic interactions not only increase the encounter rate but also promote the formation of “folding-competent topologies in the encounter complex.”

In a follow-up to the study mentioned above, Huang and Liu⁹⁵ went on to propose another phenomenon that might help to explain the kinetic advantage enjoyed by IDPs. They performed multiple Gō model simulations in which the parameters controlling the strengths of interactions within pKID (α) and between pKID and KIX (β) were systematically varied. α is effectively a measure of the disorder of pKID, and the authors found that when pKID was highly disordered, its binding was a lot less sensitive to changes in β than when it was ordered. Their interpretation of this was that binding of disordered proteins is less sensitive to changes in the environment (such as mutations, or changes in T) that would impact the binding interaction energy: the authors term this the “kinetic buffer effect.”

Although the Gō model simulations discussed above have taught us much about coupled-folding and binding, there are limitations to their use. Most importantly, they can only be applied in situations where an experimental structure for the native state exists. They also rely on that experimentally-determined structure being an accurate representation of the protein in aqueous solution, which is not always the case.⁹⁶ In addition, the dihedral angle potentials used in Gō models are often taken from the distributions of dihedral angles within the protein data bank⁹⁷ (PDB): these PDB distributions are known to be biased towards helical conformations. A similar bias exists for Gō models whose torsion angles target the native state itself. To assess the importance of this helical bias, de Sancho and Best³⁴ simulated the association of HIF1α with CBP using a standard Gō model and a Gō model that included a dihedral correction. The simulations with the dihedral correction gave a more cooperative folding-binding transition, by destabilizing partially bound intermediates. Ganguly and Chen⁹⁸ have also noted this weakness, and suggested that Gō models developed for globular proteins are not transferable to IDPs. Instead, they argue that Gō models for IDPs need to carefully calibrated against experimental data to ensure that they can accurately reproduce unfolded state conformational ensembles and binding energies. Having calibrated a Gō model in this way, they simulated p53 extreme C-terminus binding to S100B(ββ) and pKID to KIX, finding significant differences in the mechanisms of folding and binding compared to those obtained with uncalibrated Gō models.

Another potential weakness of Gō models is that they may not correctly describe encounter complexes on the folding/binding pathway if they are dominated by non-native interactions. In addition to studying the impact of the helical bias in the dihedral potential, de Sancho and Best³⁴ considered Gō model simulations of HIF1α-CBP that included favourable non-native interactions. This lowered the free energy barrier to binding and resulted in faster binding, improving the agreement with experiment – a phenomenon referred to as “non-native steering”. Huang and Liu⁹⁹ also examined the effect of adding non-native interactions to a Gō model, by including a non-specific, favourable hydrophobic interaction in simulations of pKID-KIX. They also found that non-native interactions increased the binding rate, by stabilizing the encounter complex. Moreover, they found that this effect was greater for complexes involving IDPs than for complexes involving folded proteins “thereby indicating that weak non-native hydrophobic interactions further amplify the kinetic advantages of IDPs.” They also found, however, that strong non-native interactions were more likely to result in aggregation for IDPs than for globular proteins.

Implicit Solvent Simulations

As noted above, two of the principal weaknesses of Gō models are that they may not correctly sample configurations dominated by non-native interactions, and that they do not provide an atomic-level description. Both of these problems can be overcome with atomistic simulations using force fields that attempt to account for the underlying physics of the system.¹⁰⁰ Gō model simulations also do not specifically include effects due to solvent. Instead, the role of the solvent is limited to the role that it plays in determining the native structure. When performing simulations with models that do not explicitly include native contacts, we cannot treat the solvent in this way, and must account for its presence. The most obvious way to do this is to include an explicit representation of each individual water molecule, but this significantly increases the system size and computational cost (Figure 3). An alternative is to use implicit solvation,^{101,102,103,104} in which we explicitly include only the solute degrees of freedom, and consider that the mean influence of solvent on equilibrium properties can be captured by the free energy cost of solvating the solute in a given configuration.¹⁰² Whilst this is in principle a formally exact procedure, the problem becomes the determination of the form of the solvation free energy function (which should include many-body effects). If a relatively simple form can be assumed for the solvation free energy, however, such that it can be calculated rapidly, simulations are far faster than those employing explicit solvent because: (a) there are fewer particles for which forces must be explicitly calculated, and (b) the friction due to the solvent is eliminated. This speed-up has obvious benefits for sampling during production simulations; equally important is that implicit solvent simulations are sufficiently fast that details of conformational equilibria from protein folding/unfolding can be explicitly incorporated into force field parameter optimization.^105,106

Using one such optimized force field,¹⁰⁵ Ganguly and Chen¹⁰⁷ performed MD simulations of pKID and its non-phosphorylated analogue KID. Using implicit solvent in combination with temperature replica exchange MD (REMD)¹⁰⁸ they were able to obtain well-converged conformational ensembles with 200 ns of simulation per replica. KID only binds to KIX in its phosphorylated form, pKID, and the authors did not attempt to simulate either protein in the presence of KIX. They did observe, however, that the protein conformational ensembles have similar helical content, but different conformational substates. In particular, they observed that phosphorylation restricts the conformational space accessible to a specific loop within KID, and suggest that this would lower the entropic cost associated with coupled folding and binding, explaining why pKID binds KIX but KID does not. Zhang, Ganguly and Chen⁵⁶ used a similar approach to study the synergistic coupled folding and binding that occurs between NCBD and ACTR. In this case, they found that 100 ns of REMD simulation was insufficient to obtain converged conformational ensembles of the individual proteins and complex, illustrating the challenges associated with simulation of these systems. They were still able to make qualitative observations on the disordered state ensemble, noting in particular that NCBD is well structured in the absence of ACTR, but adopts a different structure to that observed in the complex. High temperature simulations allowed the authors to observe unfolding/unbinding, and conclude that it occurs via an induced fit mechanism. Chen¹⁰⁹ also used implicit solvation simulations to probe the mechanism of coupled folding and binding in the interaction between the extreme C-terminus of p53 and S100B(ββ). p53 is notable in that it is one of the few IDPs that is known to adopt different folded conformations in different complexes²⁷ and Chen observed that all of its folded conformations are sampled in the absence of any binding partner. This suggests a conformational selection mechanism for folding/binding, which Chen tested by calculating PMFs to construct 2D energy surfaces considering the centre of mass separation and the extent of folding. He found that p53 needs to unfold at intermediate distances from S100B(ββ), binding in an unstructured conformation. This led him to conclude that the pre-existence of folded-like conformations need not be evidence of conformational selection.

Implicit solvent simulations allow us to probe conformational transitions on timescales that would be difficult, or even impossible, to achieve with explicit solvation. But the removal of the solvent degrees of freedom is an approximation that inevitably limits the amount of information that we can obtain, and simplified continuum representations of water will fail in situations^110,111,112 where there are correlations between the solute and water structure.²⁶ There are also important limitations to the methodology itself^113,114,115 and, for these reasons, it would ultimately be desirable to be able to perform simulations in which both solvent and solute are explicitly included with atomic resolution.

High Temperature Unfolding Simulations

The principle of microscopic reversibility¹¹⁶ requires that, for any system at thermodynamic equilibrium, “the total number of molecules leaving a given state in unit time shall on the average equal the number arriving in that state in unit time, (and) that the number leaving by any particular path shall on the average be equal to the number arriving by the reverse of that particular path.” What this tells us is that the mechanism of coupled folding and binding should be the reverse of the mechanism of coupled unfolding and unbinding, and therefore that any information that we can obtain about the unfolding/unbinding mechanism will be highly relevant to the folding and binding problem. This is a result that has been heavily exploited in the protein folding field, because the unfolding process is much more easily simulated than the folding process. While folding and unfolding are both rare events under equilibrium conditions, proteins can be denatured by force, chemical denaturants or high temperature.^117,118

However, it has been shown that applying force to unfold a protein results in a different mechanism to that obtained in the absence of force,^119,120 and adding chemical denaturants can also alter the mechanism by which protein unfolding occurs.¹²¹ In high temperature simulations, the principle of microscopic reversibility tells us that folding at 450 K will be the reverse of unfolding at 450 K, but not that folding at 298 K will necessarily be the reverse of unfolding at 450 K. Dinner and Karplus¹²² used lattice simulations to show that the most probable unfolding paths can depend on the temperature, and that intermediates present at low temperature may not be present at high temperature. Numerous MD simulations of protein unfolding at high temperature have been performed,¹²³ however, and it has been argued “that MD simulations at high temperature provide a credible description of protein unfolding at experimentally accessible temperatures”,¹¹⁷ even if in some cases “the order of loss of specific native contacts was not conserved across these temperatures.”¹¹⁷

For the study of coupled folding and binding, high-temperature unfolding and unbinding simulations have been most heavily exploited by Hai-Feng Chen and co-workers. They have applied this method to study the coupled folding and binding that occurs in p52-MDM2,¹²⁴ siRNA-PAZ,¹²⁵ pKID-KIX,¹²⁶ mRNA-TIS11D,¹²⁷ RNA-U1A (an interesting case where it is actually the RNA molecule that folds upon binding),¹²⁸ brinker-DNA¹²⁹ and LEF-1-DNA.¹³⁰ The methodology used in these studies is well established: all atom simulations of the individual proteins and the complex are performed at 298 K to generate reference states for the folded/bound structures; equivalent simulations are performed at 498 K, during which unfolding and unbinding will typically occur.

The data obtained from these high temperature simulations can be used to calculate a range of kinetic and thermodynamic properties, as well as to directly observe the mechanism of coupled unfolding and unbinding (and therefore coupled folding and binding). In simulations of pKID-KIX unfolding and unbinding,¹²⁶ for example, Chen used this approach to: determine that pKID follows different folding pathways in the bound and apo states; to identify the sequence of events that occurs in the coupled folding and binding of pKID, including “that KIX-binding induces the folding of pKID”, and to identify (by calculating φ values^90,91) the key residues in the folding of bound pKID. Importantly, the simulations provide this information with a level of detail that cannot be achieved using coarse-grain simulations, such as an atomic-level description of the H bonding interactions that help to stabilize the binding interface.

All-atom Simulation at Room Temperature

Current limitations in computing power mean that equilibrium simulations of coupled folding and binding have not been achieved. And even if such simulations were possible, it is debateable that this approach represents efficient use of available resources. If we are interested in studying the mechanism of coupled folding and binding, the size and complexity of the system means that a typical equilibrium simulation will spend the vast majority of its time locating the binding site by diffusive search (if binding) or awaiting a fluctuation sufficient to drive it over the energy barrier (in the case of unbinding). If we can find a way to focus our sampling on degrees of freedom relevant to the reaction, then all-atom simulations become a lot more feasible. Zhang et al.¹³¹ have adopted such an approach, employing targeted MD¹³² to study the interaction between the calmodulin binding doman, an IDP, and calmodulin. In their simulations, a harmonic biasing potential was added to the energy function based on the root mean square deviation (RMSD) of the structure at time t from the reference folded/bound structure. Starting from an unbound/unfolded state, they decreased the target RMSD by 0.5 Å over 300 ps, before allowing the system to equilibrate for 400 ps and then repeating the cycle until they reached an RMSD of 1.5 Å from the reference state. This took a total of ~25 ns and allowed the authors to identify the mechanism by which the coupled folding and binding occurs. Higo et al.¹³³ used another enhanced sampling technique, multicanonical MD¹³⁴ (McMD), to study the binding of the IDP N-terminal repressor domain of neural restrictive silencer factor (NRSF) to the paired amphipathic helix (PAH) domain of mSin3. In the McMD approach, MD is performed at constant temperature on a deformed potential energy surface, generating “a multicanonical ensemble characterized by a flat energy distribution.”¹³⁴ This multicanonical ensemble is then reweighted to generate a canonical ensemble. From their simulations, Higo et al. found that, while not natively structured, NSRF does not occupy an ensemble of random conformations, but rather fluctuates among a variety of partially structured conformations. They also found that the system does not form only a single native-like complex, but multiple complexes with a range of structures. As a result of these observations, and the atomic-level description obtained from their simulations, the authors ultimately concluded that the coupled folding and binding occurs by “an integrated mechanism, where the population-shift (conformational selection) and the induced-fit work sequentially and cooperatively to enhance the complex formation:” the “extended conformational selection” mechanism,⁸² discussed above.

An alternative approach to the study of complexes that undergo coupled folding and binding has been to simulate the initial unbound/unfolded state and final bound/folded state separately. Performing equilibrium simulations of only the two end states of the reaction, with no attempt to sample the pathways by which they interconvert, means that we obtain no direct information about the mechanism of coupled folding and binding. But it does not mean that we cannot learn anything about it. Kamberaj and van der Vaart¹³⁵ were the first to employ such an approach, studying the complex between the protein Ets-1 and DNA in which the HI-1 helix of the protein actually unfolds upon DNA binding. From their simulations, each of 15 ns, the authors observed that in apo-Ets-1, the motion of helix HI-1 is correlated with that of helix 4, whereas in the Ets-1-DNA complex, the motion of these two helices is anti-correlated. They found that this change was caused by the formation of hydrogen bonds between helix 1 and the DNA, and “that the hydrogen bonds between H1 and DNA act as a conformational switch and show that the presence of DNA is communicated from H1 to H4, destabilizing HI-1”. Wostenberg et al.¹³⁶ used the same approach to study the interaction between the natively structured protein RAP74 and the IDP C-terminal domain of FCP1. Interestingly, they identified that RAP74 adopts a significantly different conformation in the bound state than in the unbound state (i.e., despite being natively structured it also undergoes ‘folding’ upon binding), and that “FCP1 retains substantial conformational flexibility in the RAP74-FCP1 complex, that is, the complex is fuzzy”. Janowska et al.¹³⁷ used this approach to study the interactions of one IDP, the GTP-ase binding domain (GBD) of the protein WASP, with two distinct binding partners, the VCA domain of WASP and a fragment of the protein EspFu. Knott and Best³⁷ have used atomistic simulations to study the unbound state of the nuclear coactivator binding domain of the transcriptional coactivator CBP, known as NCBD; they found evidence for significant native secondary structure formation in the unbound state, as well as a preference for the formation of contacts near to the interface for binding the protein ACTR. This suggests a mechanism for how NCBD may be able to take advantage of being intrinsically disordered, whilst still retaining elements of the binding interface in the unbound state.

Future Directions

As discussed above, and in spite of recent advances, there is probably room for improvements in the force field parameters used for MD simulation, especially with regard to unfolded/disordered states. However, there is a limit to how far systematic reparameterization can take us: the accuracy of force fields is also limited by the underlying mathematical functions used to represent the physics of the systems. By necessity, these mathematical functions provide only an approximate description of the underlying physics, with various simplifications introduced to make the simulation of large systems computationally feasible. These simplifications inevitably introduce errors into the calculations, and a number of approaches have been used to try and reduce their impact, from adding additional point charges^{138,139,140,141,142} to extra terms in the potential function.¹⁴³ Perhaps the most promising, and eagerly anticipated, development in force field design, however, is the inclusion of an explicit representation of polarizability. One of the key approximations used in force fields commonly employed for biomolecular simulation is that the electrostatic properties of molecules can be represented using point charges at the nuclear sites. In reality, the charge distribution within a molecule changes in response to its environment: molecules are polarizable. Polarizability is expected to be important in many biological situations. Calculations have already indicated that polarizability influences protein folding,¹⁴⁴ and it may be even more important in coupled folding and binding: electrostatic interactions are known to play a vital role in this process,^145,146 and QM calculations have shown that the charge distribution within a ligand changes when it binds to a protein,¹⁴⁷ and that the charge distribution in a peptide changes according to its conformation.¹⁴⁸

Multiple polarizable force fields are currently being developed,^149,150 including several based on the CHARMM^151,152,153 and AMBER^154,155,156 force fields commonly used for biomolecular simulation. The great drawback with polarizable force fields is that the extra complexity in the potential function makes them significantly slower than all-atom force fields. With coupled folding and binding already at (or beyond) the limit of what can be simulated with an all atom force field, an important question becomes: are the gains in accuracy obtained with a polarizable force field sufficient to justify the increased computational cost, and in particular the reduced level of sampling compared to what could be obtained using a non-polarizable force field and the same computational resources?

For the time being, equilibrium all-atom MD simulations of coupled folding and binding are out of reach of the majority of researchers, especially if they wish to use a polarizable force field. It is clear that the best opportunity for obtaining atomic-resolution information on coupled folding and binding lies in the use of enhanced sampling methods. Broadly speaking, these methods fall into two categories: those that enhance the sampling of the equilibrium distribution, and those that focus sampling on the transition of interest. For enhancing sampling of equilibrium distributions, replica exchange MD¹⁰⁸ (REMD) and Markov state models^157,158 have both been successfully applied to the study of protein folding.^159,160 Alternatively, umbrella sampling¹⁶¹ can be used to enhance sampling along a given reaction coordinate, though care must be taken to define a coordinate appropriate for the system being studied.¹⁶² For coupled folding and binding, the fraction of native bound contacts would seem like a reasonable starting point. In order to sample transitions between unbound and bound states from an equilibrium distribution, a number of approaches are possible, for example, transition path sampling^163,164 or forward flux sampling.^165,166,167 These can be limited by the requirement that the states to be transitioned between must be known in advance, but transition-path sampling has been successfully applied to the study of protein folding.¹⁶⁸ A third possibility is path optimization, in which the path between two end states is not directly sampled but explicitly optimized. Such an approach has already been applied to the study of coupled folding and binding by Wang et al.¹⁶⁹ who used a steepest descent algorithm to optimize the path between the folded/bound and unfolded/unbound states of the IA3-YprA complex. In their study, Wang et al. also used Gō models to study the same system. And although the information from these Gō model simulations was not used in their atomistic simulations, this does hint at another possibility for enhancing sampling: the use of multiscale modelling. At its simplest level, one could, for example, use implicit solvent simulations to generate initial, final and intermediate states for transition path simulations including explicit solvent. At a more sophisticated level, we have shown that it is possible to directly connect additive and polarizable simulations via a Hamiltonian replica exchange scheme, significantly enhancing sampling with the polarizable force field.¹⁷⁰ Most ambitiously, one could even imagine coupling implicit solvent (or even Gō model) simulations to atomistic simulations via a replica exchange scheme with multiple intermediate states.

Conclusion

The biological significance of IDPs is well-established, but the mechanism by which they interact with their binding partners remains poorly understood, despite its importance to their biological function. Given the difficulty (or even impossibility) of obtaining atomic level descriptions of coupled folding and binding events directly from experiment, molecular simulation represents one of the most promising tools available for their study. Simulating coupled folding and binding events is challenging, but significant progress has been made, particularly through the use of simplified models based on reduced representations of the full systems. The Holy Grail remains, however, the simulation of coupled folding and binding in atomic detail under equilibrium conditions. The size and complexity of the systems to be simulated makes this an extremely challenging problem, and the road to its completion is likely to be long and difficult: force field parameters will probably need modifying, and force field potential functions themselves may need to take a different form. But as recent progress in the simulation of protein folding has shown us, with intelligent use of resources and clever application of enhanced sampling schemes, these challenges are far from insurmountable. As ever, close comparison with experimental results, for example binding rates or φ-values,¹⁷¹ will be essential in order to benchmark the accuracy of the results.