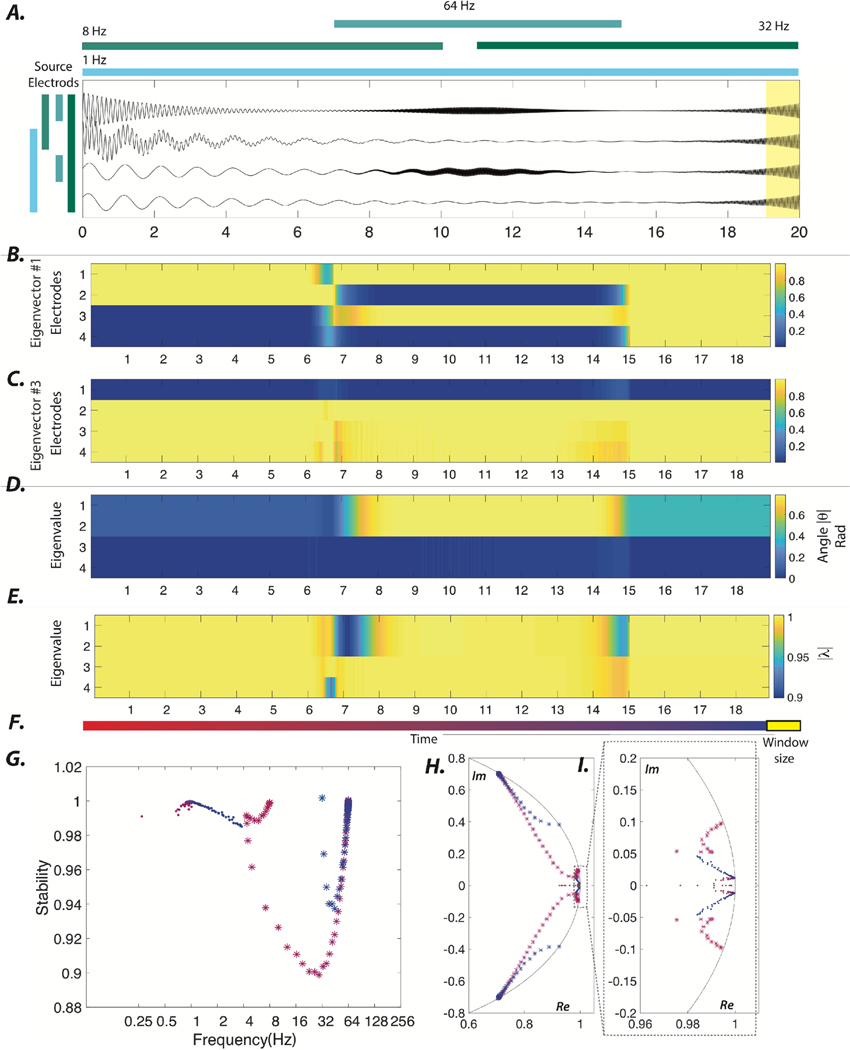
Figure 1.
Dynamical stability of synthetic time series. (A) To gain intuition, we constructed synthetic time series sampled at 512 Hz that capture an underlying emerging process defined by an enveloped (exponential, Gaussian) sinusoid. Briefly, the simulated time series captures various partially overlapping spatiotemporal patterns of oscillations with varying frequencies. The colored bar at the top of the panel represents the duration over which the oscillation with that specific frequency is present. The colored bars on the left code the sources of the oscillations, where the top source leads the following source by . The yellow shaded area on the right indicates the size of the moving window. (B), (C) The absolute values of the normalized eigenvectors 1 and 3 obtained using a 1 s window shifted by 100 ms intervals. (D), (E) The evolution of the angle (reflecting the oscillation frequency) and radius (reflecting the stability) associated with the four eigenvectors of the 4-sensor system. Note that the changes in the angle and radius associated with higher frequency eigenmodes (i.e. eigenmodes 1 and 2) between the 6 and 8 s timepoints mark the transition and emergence of high frequency (64 Hz) oscillations between electrodes 1 and 3. (F) The temporal progression of the sliding window illustrated in changing hues of red; the yellow box represents the relative size of the moving window used to estimate the linear model. (G) The temporal evolution of the frequency (Hz) and stability associated with the first eigenmode (‘dot’) and third eigenmode (‘star’). (H) The temporal evolution of the four eigenvalues in the Argand complex plane. (I) A zoomed-in version of the panel (H) is provided to show the changes in the angle and radius of the low angle eigenvalues in greater detail. Panels (G)–(I) use the same color-coding as in panel (F). In sum, this example demonstrates how the dynamical properties of oscillatory sources that are spatiotemporally overlapping are reflected in the eigenvalue-eigenvector pairs and their fluctuations over time.