Figure 4.

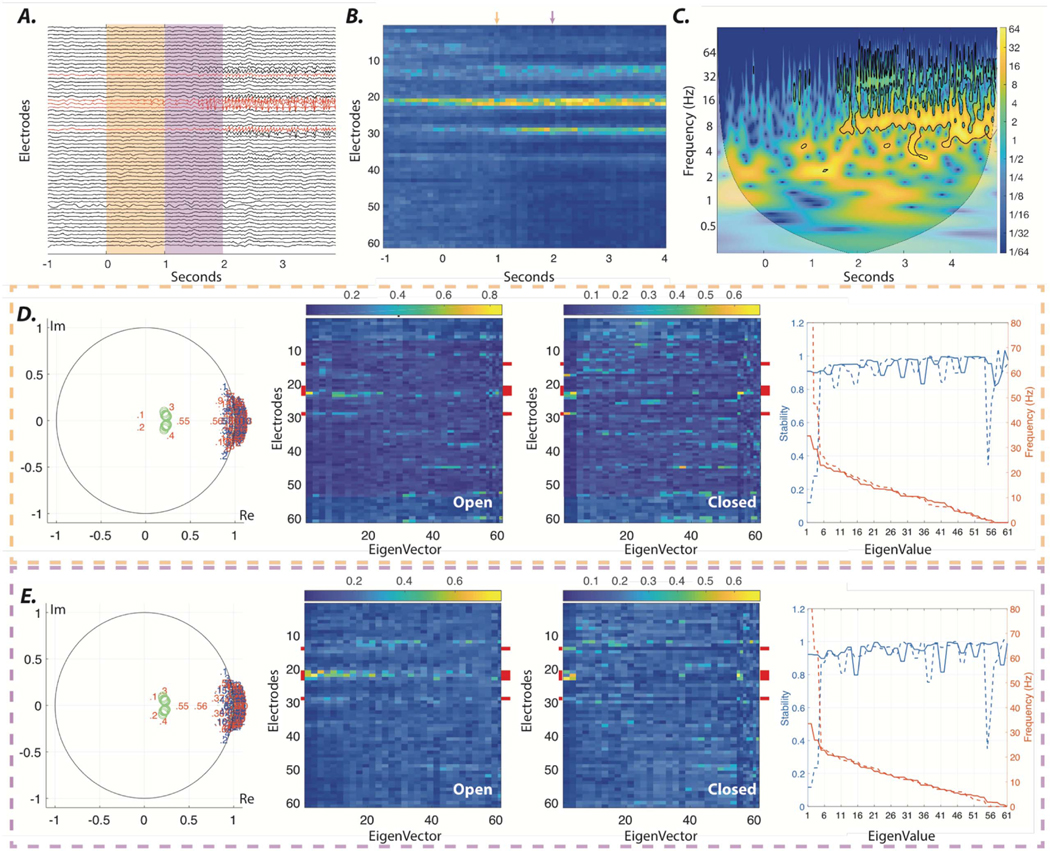
Stabilizing ictal onset oscillations using closed-loop feedback control. (A) Seizure onset sampled from a patient with iEEG recordings from which we can clearly localize the SOZ. (B) Mean absolute values of all eigenvectors, whose associated eigenvalues reside at β- and γ—band frequencies (15–50 Hz) across the 1-sec sliding windows. The orange and purple arrows highlight the high loading of a few electrodes in two selected windows at the seizure onset presented in panel A. (C) Wavelet decomposition of a SOZ electrode highlights the emergence of oscillations at high frequencies following seizure onset. (D) The left panel shows the distribution of the estimated eigenvalues at seizure onset (orange window in panel A). Eigenvalues are sorted based on their frequencies, from highest to lowest. Blue numbered dots represent the empirically estimated values. We simulate the effect of closed-loop static feedback between a few electrodes (marked by red in panel A), by representing eigenvalues of the closed system (red numbered dots). Only five electrodes with the highest eigenvector loading at seizure onset (as seen in panel B) were selected as sensing and stimulating electrodes to mimic the limited channels of implantable neurostimulation devices. The static output feedback gains were calculated using the generalized pole placement method [31], with the control-theoretic objective of shifting all the higher frequency (>15 Hz) eigenvalues of systems that were estimated from ten consecutive sliding widows following the seizure onset to the predefined zones, represented by green circle (for more details see supplementary information). The two middle panels show the absolute values of eigenvectors of the open and closed systems. The right panel shows the stability (i.e. absolute values of eigenvalues) and frequency of all eigenvalues in both open (solid lines) and closed (dashed lines) systems. Note the reduced stability of all the closed system eigenvalues with associated eigenvectors with high loading on stimulating electrodes (marked by red in middle panels); namely, eigenmodes 1–4 (See supplementary figure 4 for statistical test results). (E) Same results as those represented in panel D, calculated for the purple window in panel A. Together, this demonstration suggest that the calculated static feedback can similarly stabilize the seizure activity across all seizure onset windows.