Fig. 3.

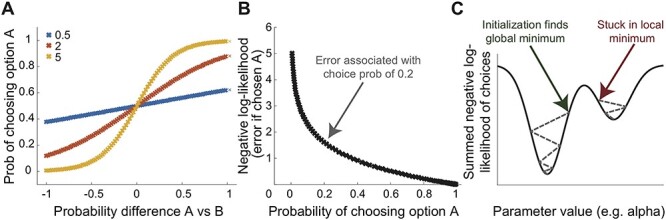
Softmax temperature, negative log-likelihood and error minimization: (A) obtained choice probabilities are shown for three different values of the inverse temperature parameter of the softmax function (‘beta’). Larger inverse temperature values correspond to a steeper function and thus less noisy choices. Note that the range of the beta values will depend on the range of the ‘decision variable’, here the probability difference between A and B which can vary between [−1, 1]. It can be helpful to scale decision variables in comparable ranges so that the scale of the temperature parameter becomes interpretable (note that only multiplicative scaling, but no additive shifting, should be applied to decision variables). (B) The choice probabilities are log-transformed and inverted (−log(choiceProb)) to obtain the negative log-likelihood of each choice. This not only makes it practically possible to compute the likelihood (product) of all choices because the log of the product is the sum of the log-transformed values. But it also means that very wrong predictions (e.g. a low 0.2 predicted probability of choosing option A when the participant actually choses option A) will be given a stronger weight in the overall error. (C) The summed negative log-likelihood of all choices needs to be minimized to obtain the best fit. This is done internally by fitting algorithms by varying the parameter values (here just alpha) until the parameter value that is associated with the minimum error is found. Because of local minima, it is sometimes important to run fitting algorithms with multiple parameter starting values.