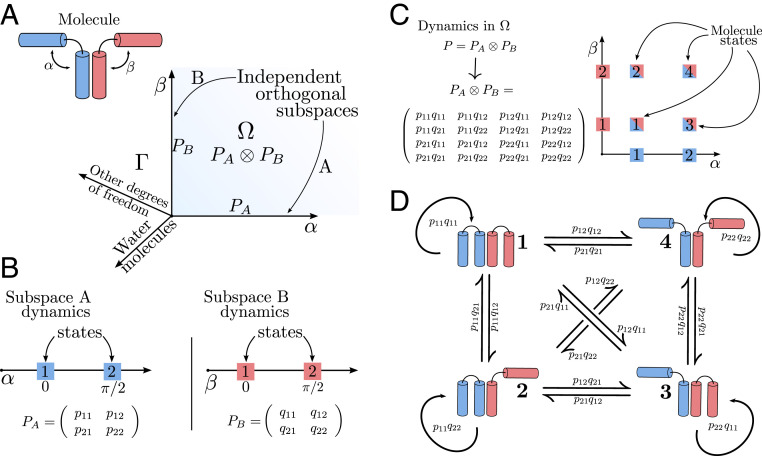
Fig. 2.

Operator decomposition and discretization on a test molecule. (A) A test molecule is decomposed into two subsystems (blue and red). The two angles $\alpha$ and $\beta$ span subspaces $A$ and $B$ corresponding to the two subsystems, respectively. The space $\mathrm{\Gamma }$ is composed of all system degrees of freedom. The space $\mathrm{\Omega }$ is the Cartesian product of $A$ and $B$ and its dynamics are described by Perron–Frobenius operators $P_A$ and $P_B$, respectively. The dynamics in $\mathrm{\Omega }$ are given as the tensor product $P_A\otimes P_B$. (B) The molecule has metastable states at $\alpha =0,\pi /2$ and $\beta =0,\pi /2$; the subspaces $A$ and $B$ can be discretized into MSMs with transition probability matrices ${\mathit{P}}_A$ and ${\mathit{P}}_B$. The quantities $p_{ij}$ and $q_{ij}$ are the transition probabilities from state $i$ to $j$ of subspaces $A$ and $B$, respectively. (C) The discretized dynamics in $\mathrm{\Omega }$ are given by the tensor product ${\mathit{P}}_A\otimes {\mathit{P}}_B$, yielding the four states of the full molecule. (D) Illustration of the four possible states of the molecule and the transitions between them.