Non-Markovian modeling of protein folding

Significance

Protein-folding kinetics is often described as Markovian (i.e., memoryless) diffusion in a one-dimensional free energy landscape, governed by an instantaneous friction coefficient that is fitted to reproduce experimental or simulated folding times. For the $\alpha$-helix forming polypeptide ${\mathrm{a}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{e}}_9$ and a specific reaction coordinate that consists of the summed native hydrogen-bond lengths, we demonstrate that the friction extracted from molecular dynamics simulations exhibits significant memory with a decay time that is in the nanosecond range and thus, of the same order as the folding and unfolding times. Our non-Markovian modeling not only reproduces the molecular dynamics simulations accurately but also demonstrates that memory friction effects lead to anomalous and drastically accelerated protein kinetics.

Abstract

We extract the folding free energy landscape and the time-dependent friction function, the two ingredients of the generalized Langevin equation (GLE), from explicit-water molecular dynamics (MD) simulations of the $\alpha$-helix forming polypeptide ${\mathrm{a}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{e}}_9$ for a one-dimensional reaction coordinate based on the sum of the native H-bond distances. Folding and unfolding times from numerical integration of the GLE agree accurately with MD results, which demonstrate the robustness of our GLE-based non-Markovian model. In contrast, Markovian models do not accurately describe the peptide kinetics and in particular, cannot reproduce the folding and unfolding kinetics simultaneously, even if a spatially dependent friction profile is used. Analysis of the GLE demonstrates that memory effects in the friction significantly speed up peptide folding and unfolding kinetics, as predicted by the Grote–Hynes theory, and are the cause of anomalous diffusion in configuration space. Our methods are applicable to any reaction coordinate and in principle, also to experimental trajectories from single-molecule experiments. Our results demonstrate that a consistent description of protein-folding dynamics must account for memory friction effects.

Biological macromolecular function relies on coupled processes that take place on widely different timescales; this makes the theoretical description of such systems challenging. For proteins, the topic of this paper, folding occurs in the range of microseconds to many minutes or even hours and involves bond vibrations and hydration water motion on subpicosecond times (1–3). In order to enable large-scale simulations as well as meaningful theories, which should concentrate on the essential features of such processes, several methods for the elimination of irrelevant degrees of freedom have been introduced. For the classical dynamics of an interacting many-body system, the rigorous treatment is based on the Liouville equation and employs the projection operator formalism to integrate out all degrees of freedom except one or a few reaction coordinates (4, 5). Instead of $6N$ equations of motion for all positions and momenta of an $N$-particle system, the dynamics is described by few equations for the observables of interest. This coarse-graining procedure leads from a deterministic Hamiltonian to a stochastic description by the generalized Langevin equation (GLE), which for the case of a one-dimensional coordinate $q\left(t\right)$, reads (4–7)

$$m\ddot{q}\left(t\right)=-\nabla U\left[q\left(t\right)\right]-{\int }_0^t\mathrm{d}s\hspace{0.17em}\mathrm{\Gamma }\left(t-s\right)\dot{q}\left(s\right)+F_R\left(t\right),$$ [1]

where $m$ is the effective mass of the coordinate $q$. The potential of mean force $U\left(q\right)$, which for proteins, corresponds to the folding free energy landscape, is obtained from the equilibrium probability distribution $\rho \left(q\right)$ via $U\left(q\right)=-k_{B}T\ln \rho \left(q\right)$, where $k_{B}T$ is the thermal energy with $k_B$ the Boltzmann constant and $T$ the absolute temperature. The elimination of degrees of freedom introduces non-Markovian effects in terms of the memory function $\mathrm{\Gamma }\left(t\right)$, which describes time-dependent friction and thereby, couples the present dynamics to the past states, and stochastic effects in terms of the random force $F_R\left(t\right)$. In equilibrium, the random force $F_R\left(t\right)$ is related to $\mathrm{\Gamma }\left(t\right)$ via the fluctuation–dissipation theorem $⟨F_R\left(t\right)F_R\left(t^{\prime }\right)⟩=k_{B}T\mathrm{\Gamma }\left(|t-t^{\prime }|\right)$ (7). The derivation of the GLE in Eq. 1 relies on several approximations (8–11). Thus, for a given reaction coordinate that is a nonlinear function of the microscopic coordinates, the validity of Eq. 1 is not guaranteed and needs to be explicitly checked.

The folding free energy $U\left(q\right)$ can be straightforwardly obtained from simulations; it can also be obtained from single-molecule experiments (12–15). Clearly, there is no guarantee that a given reaction coordinate, which could be an experimental observable such as the distance between two attached fluorophores, is a good reaction coordinate, meaning that it leads to a Markovian description of the folding process. Different reaction coordinates have been proposed for the efficient description of protein-folding simulations (16); schemes to construct reaction coordinates that optimally yield the transition state, which separates unfolded and folded basins of attraction from each other, have been developed (17). As an alternative to continuous reaction coordinates, Markov models describe protein dynamics in terms of a set of metastable states (18, 19), for which full access to the underlying microscopic coordinates is typically needed. These works have in common that descriptions are sought that minimize memory effects, so that stochastic Markovian theory applies. In the opposite direction, various methods were developed to extract the memory function $\mathrm{\Gamma }\left(t\right)$ from time series data for a given reaction coordinate (9, 20–25), but the complexities of the GLE, in particular for a nonlinear protein-folding free energy in combination with a numerically determined memory function, prevented predictions of protein-folding times from the GLE, with the notable exception of dialanine (26). This is why in protein-folding theory, the Markovian Langevin equation (LE), where the memory integral is replaced by an instantaneous friction term, is predominantly used. Such a Markovian theory yields many useful insights into protein-folding dynamics and culminated in the comparison of transition-path times and mean folding times (27, 28). However, the success of free energy folding theory on the Markovian level relies partly on the fact that the friction, which determines the prefactor of the Kramers folding time, is normally used as a fitting parameter. Even when the friction is allowed to vary with the reaction coordinate and is extracted from simulations, it is typically computed from folding or reconfiguration times, which by construction, leads to self-consistent predictions of the kinetics (29, 30). In fact, recent experiments revealed significant inconsistencies when comparing directly measured free energy barrier heights with those inferred from transition path and folding times (15), which were suggested to be due to memory effects (31, 32). The same inconsistencies are obtained when the friction of a reaction coordinate is not fitted to folding times but rather, extracted directly from simulation trajectories and used in the framework of Markovian theory, as we demonstrate here.

In our approach, instead of searching for a good reaction coordinate, we employ a standard one-dimensional coordinate that consists of the sum of the separations between native contacts. We use accurate tools for extracting all parameters of the GLE from molecular dynamics (MD) simulations for the helix-forming polypeptide ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ in water. The free energy $U\left(q\right)$ shows multiple minima separated by low barriers, indicative of the sequential formation of the helix, while the longest decay time of the multiexponential memory function $\mathrm{\Gamma }\left(t\right)$ is of the order of the unfolding time. These properties render ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ as a very sensitive test of kinetic theory. We simulate the resulting GLE by Markovian embedding techniques. By comparison of the MD and GLE results for the mean folding and unfolding times, we demonstrate that the one-dimensional GLE is an accurate and practical tool for the description of protein-folding dynamics. On the other hand, the Markovian version of the overdamped GLE cannot describe the folding and unfolding kinetics of the peptide as long as the friction is not a fitting parameter but rather, taken as extracted from the MD simulations. This stays true even when the friction coefficient is allowed to depend on the reaction coordinate. As predicted by the Grote–Hynes theory, memory typically accelerates barrier crossing, where the acceleration magnitude depends primarily on the ratio of the memory time and the distance between the minimum and the barrier in reaction coordinate space (33–38). This memory-induced speedup of folding and unfolding is found to be accompanied by pronounced anomalous diffusion in reaction coordinate space. Our results are corroborated by a systematic Kramers–Moyal coefficient (KMC) analysis, which shows that higher-order quartic KMCs are nonnegligible and that the linear and quadratic KMCs vanish in the short time limit, as expected in the presence of non-Markovian effects. This implies that the description of protein folding in terms of the Fokker–Planck equation is only valid above a certain timescale that needs to be suitably chosen. We also find that a spurious reaction coordinate–dependent friction profile arises when non-Markovian protein dynamics is described using a Markovian model.

Results and Discussion

MD Simulations and GLE Parameter Extraction.

The effective GLE is constructed from a 10-$\mathrm{\mu }$s-long MD trajectory for ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ in water, which is the simplest polypeptide that forms an $\alpha$-helix (39) (Methods and SI Appendix, section 1 have details). As a reaction coordinate, we use the summed separations between the H-bond donor nitrogen of residue n and the acceptor oxygen of residue n + 4,

$$q\left(t\right)=\frac{1}{3}\sum _{i=2}^4\Vert {\mathbf{r}}_i^N\left(t\right)-{\mathbf{r}}_{i+4}^O\left(t\right)\Vert ,$$ [2]

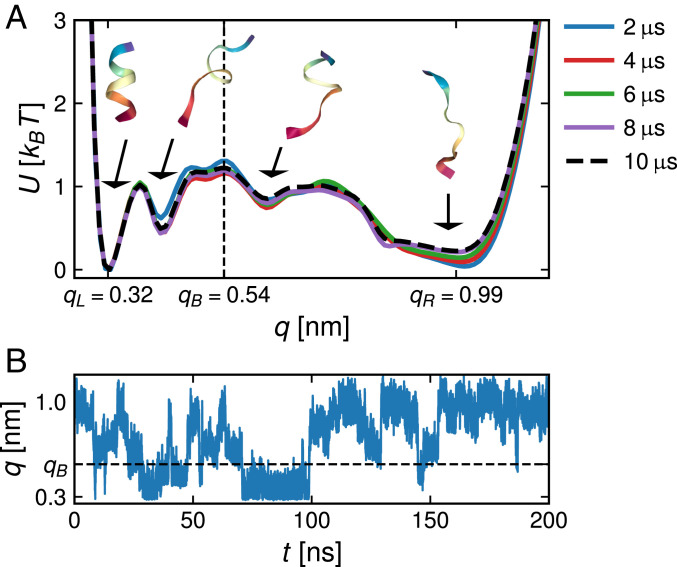
which characterize the left-handed $\alpha$-helical conformation. In the $\alpha$-helical state, $q$ has a value around $0.3\hspace{0.17em}$ nm, the mean H-bond length between nitrogen and oxygen. We will further also consider the end-to-end distance as an alternative reaction coordinate. The free energies $U\left(q\right)$ in Fig. 1A for different simulation lengths demonstrate that the simulation is fully converged after about $6\hspace{0.17em}\mathrm{\mu }$s. The free energy displays several metastable states, which are also discernible in the trajectory in Fig. 1B and make this simple polypeptide challenging for theoretical description.

Fig. 1.

(A) The free energy $U\left(q\right)$ for the mean hydrogen-bond distance reaction coordinate of ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ for different simulation lengths; representative snapshots of the polypeptide backbone in all local minima are shown. The barrier used for the calculation of unfolding and folding times is positioned at $q_B=0.54\hspace{0.17em}$ nm. (B) A $200\hspace{0.17em}$-ns-long segment of the trajectory is shown.

Using a generalization of earlier methods (40), we extract the running integral $G\left(t\right)={\int }_0^{t}ds\mathrm{\Gamma }\left(s\right)$ (SI Appendix, section 2 has details), from which the memory function $\mathrm{\Gamma }\left(t\right)$ is obtained via a numerical derivative and fitted using least-square methods to a multiexponential of the form

$$\mathrm{\Gamma }\left(t\right)=\sum _{n=1}^5\frac{{\gamma }_n}{{\tau }_n}{e}^{-t/{\tau }_n}.$$ [3]

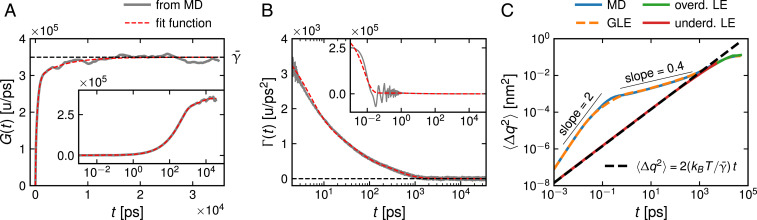
The extracted $G\left(t\right)$ (gray line) is compared with the corresponding fit (red line) in Fig. 2A; no significant deviations can be discerned. The comparison of the extracted and fitted memory function $\mathrm{\Gamma }\left(t\right)$ in Fig. 2B reveals oscillations below a picosecond, which are not reproduced by the exponential fit function but also do not play a role for the kinetics, as will be shown below. The fitted memory times ${\tau }_n$ and friction coefficients ${\gamma }_n$ are presented in Table 1; the typical reconfiguration time, which can be qualitatively inferred from the trajectory in Fig. 1B, is of the order of the longest decay time ${\tau }_5\approx 5$ ns. This means that the reaction coordinate is not particularly good since it exhibits pronounced non-Markovian effects and thus, constitutes a suitable test of our methods.

Fig. 2.

(A) Running integral $G\left(t\right)$ over the memory function; Inset shows a lin-log plot. The horizontal dashed line denotes the total friction coefficient $\overline{\gamma }$. (B) Memory function $\mathrm{\Gamma }\left(t\right)$; Inset includes short times. Gray lines correspond to the numerical data; red lines correspond to the multiexponential fit according to Eq. 3. (C) Mean-square displacement of the reaction coordinate; MD (blue line) and GLE (orange broken line) simulation results agree perfectly and exhibit superdiffusion for times up to 0.1 ps and subdiffusion up to 1 ns. Underdamped (underd.; red line) and overdamped (overd.; green line, underneath the red line) Markovian Langevin simulations agree perfectly with each other but miss the anomalous diffusion.

Table 1.

Fitted memory function parameters from Eq. 3

$n$	${\gamma }_n$ (u/ps)	${\tau }_n$ (ps)
1	$2.2\cdot 10^3$	0.007
2	$1.2\cdot 10^4$	4.6
3	$4.2\cdot 10^4$	40.3
4	$2.4\cdot 10^5$	399
5	$5.7\cdot 10^4$	4,970
$\overline{\gamma }={\sum }_n{\gamma }_n$	$3.5\cdot 10^5$

The effective mass follows from the equipartition theorem according to $m=k_{B}T/⟨{\dot{q}}^2⟩$ and turns out to be independent of $q$ and given by $m=31.3$ u (SI Appendix, section 3). The motion described by the GLE is expected to become diffusive after the inertial time ${\tau }_m=m/\overline{\gamma }$, where the total friction coefficient is given by $\overline{\gamma }={\sum }_n{\gamma }_n=3.5\cdot 10^5\hspace{0.17em}$ u/ps (Table 1). It follows that ${\tau }_m=0.1$ fs, even shorter than the MD integration time step; thus, inertial effects are completely negligible. Nevertheless, the acceleration term in Eq. 1 is kept in the GLE simulations, as it stabilizes the numerical integration. In order to estimate the importance of memory effects, the memory times ${\tau }_n$ are compared with the diffusion timescale ${\tau }_D=\beta \overline{\gamma }{L}^2/2$ (36), which is the time it takes a free Brownian particle to diffuse over a length $L$ in reaction coordinate space where $\beta =1/k_{B}T$ is the inverse thermal energy. For $L=0.22\hspace{0.17em}$ nm, the distance between the folded minimum at $q=0.32\hspace{0.17em}$ nm and the barrier at $q=0.54\hspace{0.17em}$ nm in Fig. 1, one obtains ${\tau }_D=6.8$ ns, which is of the order of the longest memory time ${\tau }_5$. This places the system in the so-called memory-acceleration regime, where memory effects are relevant and significantly accelerate barrier crossing (36–38).

Comparison of MD and GLE Simulations.

Numerical integration of the GLE is straightforwardly achieved by Markovian embedding (i.e., by transforming the GLE into a system of linearly coupled LEs) (22) (SI Appendix, section 4).

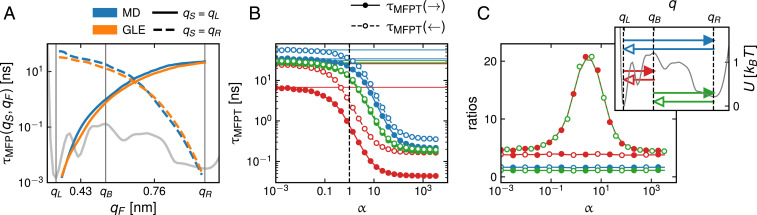
In Fig. 3A, we show profiles of the mean first-passage time (MFPT) ${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_S,q_F\right)$ for unfolding (start position $q_S=q_L=0.32\hspace{0.17em}$nm; solid lines) and folding kinetics (start position $q_S=q_R=0.99\hspace{0.17em}$ nm; broken lines) as a function of the final position $q_F$. Statistical errors are determined accounting for data correlations (41) (SI Appendix, section 5) and are smaller than the line thickness. MD and GLE simulation results (blue and orange lines, respectively) agree nicely; this demonstrates that GLE-based non-Markovian modeling of protein folding is feasible and accurate. Even first-passage time distributions from GLE and MD simulations agree satisfactorily with each other, as shown in SI Appendix, section 6.

Fig. 3.

(A) Comparison of unfolding and folding MFPTs ${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_S,q_F\right)$ from MD (blue) and GLE (orange) simulations as a function of the final position $q_F$ for start positions $q_S=q_L=0.32\hspace{0.17em}$ nm (solid lines) and $q_S=q_R=0.99\hspace{0.17em}$ nm (broken lines). The gray curve shows the folding free energy $U\left(q\right)$. (B) Dependence of different MFPTs from GLE simulations on the memory time rescaling factor $\alpha$; the corresponding start and final positions are illustrated in C, Inset. Open and filled circles correspond to open and filled arrows, respectively, in C, Inset. The colored horizontal lines denote corresponding results for the overdamped Markov limit from Eq. 10. (C) Ratios of the MFPTs shown in B. Ratios of reciprocal MFPTs do not depend on $\alpha$ (red, green, and blue lines that connect colored circles); only the ratio of the folding and unfolding times to the barrier top, ${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_R,q_B\right)/{\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_L,q_B\right)$ (open green and filled red spheres), depends on $\alpha$.

Beyond reproducing MD results, the GLE is a diagnostic tool that allows us to quantify the importance of memory effects. In order to modulate memory effects in the GLE, we rescale the memory times according to ${\tau }_n\to \alpha {\tau }_n$ for $n=\mathrm{2,3,4,5}$ while keeping the memory time ${\tau }_1$ of the fastest exponential contribution fixed. Since ${\tau }_1=7$ fs is above the simulation time step of 1 fs, this ensures that in the limit $\alpha \to 0$, we obtain a regularized model that, as we will show below, corresponds to the Markovian limit. In Fig. 3B, we show MFPTs between the three positions $q_L=0.32\hspace{0.17em}$ nm, $q_B=0.54\hspace{0.17em}$ nm, and $q_R=0.99\hspace{0.17em}$ nm as a function of the rescaling factor $\alpha$ from GLE simulations. The six different MFPTs are illustrated in Fig. 3 C, Inset by filled and closed arrows and indicated in Fig. 3B by corresponding filled and open colored spheres. We see that reducing the memory time increases all MFPTs; in other words, memory accelerates barrier crossing (36). As expected, the GLE results approach the overdamped Markov limit, denoted by the horizontal lines in the corresponding color and calculated from the exact expression in Eq. 10, without adjustable parameters as $\alpha$ tends to zero. Interestingly, for folding to the barrier (open green circles), the MFPT for $\alpha =1$ and the Markovian limit for $\alpha \to 0$ differ only by a factor of around 2.5. On the other hand, for unfolding to the barrier (filled red circles), the $\alpha \to 0$ and $\alpha =1$ MFPTs differ by a factor of around nine. This means that even when treating the total friction coefficient $\overline{\gamma }$ as a free parameter, the Markovian overdamped theory Eq. 10, because it is linear in the friction, can reproduce either the MD folding or unfolding times to the barrier but not both simultaneously. This is not due to inertial effects since the overdamped Markovian theory works perfectly for $\alpha \to 0$, as seen in Fig. 3B. Rather, memory effects influence the times of folding and unfolding to the barrier top differently. This is demonstrated by the plot of MFPT ratios as a function of $\alpha$ in Fig. 3C, where it is seen that the ratio of the folding and unfolding times to the barrier top ${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_R,q_B\right)/{\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_L,q_B\right)$, denoted by open green and filled red spheres, depends sensitively on $\alpha$. In contrast, the ratios of reciprocal MFPTs (i.e., MFPTs with interchanged start and final positions), denoted by red, green, and blue lines with identically colored open and filled circles, do not depend on $\alpha$, which shows that the memory dependence of ratios of MFPTs depends on the precise MFPT definition and by no means indicates a breakdown of the detailed balance or the law-of-mass action. In SI Appendix, section 6, we demonstrate that the memory-induced speedup is even more pronounced for transition-path times compared with folding and unfolding times, in agreement with previous findings (15, 31, 32).

The high accuracy of GLE simulations is furthermore reflected by the good agreement of the mean-square displacement $⟨\mathrm{\Delta }q{\left(t\right)}^2⟩=⟨{\left(q\left(t^{\prime }+t\right)-q\left(t^{\prime }\right)\right)}^2⟩$ from MD and GLE simulations in Fig. 2C, which exhibits pronounced subdiffusive behavior with an exponent 0.4 for times between 1 ps and 1 ns. Anomalous diffusion is often modeled by fractional theories (31, 42). Fig. 2C shows that it is accurately reproduced by multiexponential memory and that it disappears when memory effects are eliminated, in line with recent theoretical analysis (43). The overall good agreement between MD and GLE simulation results shows that the GLE in the form of Eq. 1 describes the kinetics of ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ very accurately. This is not due to our specific choice of reaction coordinate, as demonstrated in SI Appendix, section 7, where we present a similar GLE-based analysis using the ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ end-to-end distance as reaction coordinate.

Reaction Coordinate–Dependent Friction.

We so far demonstrated that the GLE in the form of Eq. 1 reproduces the MD simulation kinetics and that memory effects are significant. We now investigate whether reaction coordinate–dependent friction effects, which are not included in the GLE, are relevant. The Markovian LE that incorporates a friction function $\gamma \left(q\right)$ has been amply used to describe protein-folding dynamics (29, 30, 44). In the underdamped version, it reads

$$m\ddot{q}\left(t\right)=-U^{\prime }\left(q\right)-\gamma \left(q\right)\dot{q}\left(t\right)+\sqrt{k_{B}T\gamma \left(q\right)}\hspace{0.17em}\eta \left(t\right),$$ [4]

which for general $U\left(q\right)$, unfortunately is analytically intractable. The overdamped version

$$0=-U^{\prime }\left(q\right)-\gamma \left(q\right)\dot{q}\left(t\right)-\frac{k_{B}T}{2}\frac{{\gamma }^{\prime }\left(q\right)}{\gamma \left(q\right)}+\sqrt{k_{B}T\gamma \left(q\right)}\hspace{0.17em}\eta \left(t\right)$$ [5]

is much more useful since the MFPTs can be calculated analytically. In these expressions, the random force $\eta \left(t\right)$ has vanishing mean, and its correlator is given by $⟨\eta \left(t\right)\eta \left(t^{\prime }\right)⟩=2\delta \left(t-t^{\prime }\right)$. For constant friction, the underdamped LE (Eq. 4) can be derived from the GLE (Eq. 1) by a systematic expansion of the integral kernel (SI Appendix, section 8). The overdamped LE (Eq. 5) follows from Eq. 4 by neglecting the inertia term; the term proportional to the gradient ${\gamma }^{\prime }\left(q\right)$ cancels a spurious drift term and follows by mapping on the Fokker–Planck equation (SI Appendix, section 9) (6). In fact, from the overdamped LE with constant friction, an arbitrary friction profile $\gamma \left(q\right)$ can be created by a nonlinear transformation of the reaction coordinate (29, 30) (SI Appendix, section 10); this suggests that spatially dependent friction is related to nonlinearities in the reaction coordinate that are not straightforwardly captured by the projection techniques used to derive the GLE Eq. 1.

Various methods to extract $\gamma \left(q\right)$ from experimental or simulated trajectories have been proposed; a systematic approach involves the KMCs, which for the overdamped case and for finite lag time $\mathrm{\Delta }t$, read

$$D_k\left(q\right)=\frac{1}{k!}\frac{1}{\mathrm{\Delta }t}{⟨{\left(q\left(t+\mathrm{\Delta }t\right)-q\left(t\right)\right)}^k⟩}_{q\left(t\right)=q}.$$ [6]

The Fokker–Planck equation for the time-dependent probability distribution $P\left(q,t\right)$ in terms of the KMCs follows in the limit $\mathrm{\Delta }t\to 0$ as (7)

$$\frac{\partial P\left(q,t\right)}{\partial t}=\sum _{k=1}^{\infty }\frac{{\partial }^k}{\partial q^k}\left[D_k\left(q\right)P\left(q,t\right)\right],$$ [7]

and the underdamped case is treated in SI Appendix, section 11. According to Pawula’s theorem, for a Markovian process, all KMCs with $k>2$ vanish for $\mathrm{\Delta }t\to 0$, and Eq. 7 takes the standard form of a second-order partial differential equation (7). For a non-Markovian process [i.e., if the memory function $\mathrm{\Gamma }\left(t\right)$ in Eq. 1 has a finite range], all KMCs with $k>1$ vanish for $\mathrm{\Delta }t\to 0$, and thus, the stochastic properties of the process cannot be described by a partial differential equation for $P\left(q,t\right)$ at all (SI Appendix, section 12).

For the underdamped LE, the relation between the second-order velocity KMC $D_{vv}$ and the friction profile ${\gamma }_{\mathrm{U}\mathrm{D}}\left(q\right)$ reads (7)

$$D_{vv}\left(q\right)=\frac{1}{2\mathrm{\Delta }t}{⟨{\left(v\left(t+\mathrm{\Delta }t\right)-v\left(t\right)\right)}^2⟩}_{q\left(t\right)=q}=k_{B}T\frac{{\gamma }_{\mathrm{U}\mathrm{D}}\left(q\right)}{m^2}.$$ [8]

For the overdamped LE, ${\gamma }_{\mathrm{O}\mathrm{D}}\left(q\right)$ follows from the second-order position KMC $D_{qq}$ as

$$D_{qq}\left(q\right)=\frac{1}{2\mathrm{\Delta }t}{⟨{\left(q\left(t+\mathrm{\Delta }t\right)-q\left(t\right)\right)}^2⟩}_{q\left(t\right)=q}=\frac{k_{B}T}{{\gamma }_{\mathrm{O}\mathrm{D}}\left(q\right)}$$ [9]

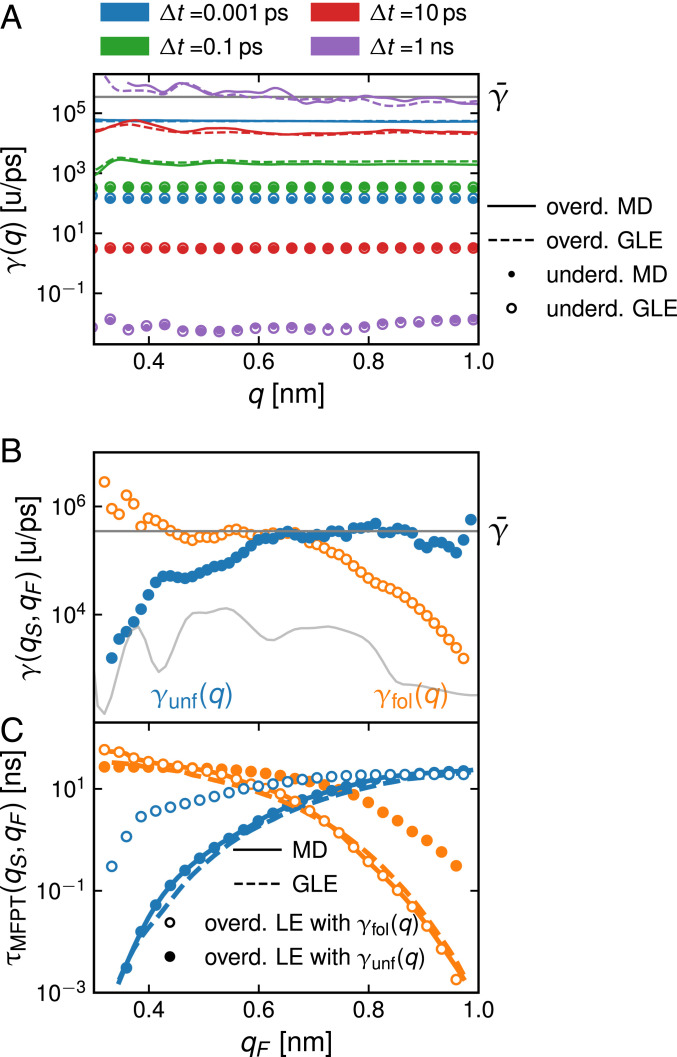
(SI Appendix, section 9). For the numerical computation of the KMCs, we use kernel-density estimators (45) (SI Appendix, section 13). In Fig. 4A, we show the friction profiles ${\gamma }_{\mathrm{U}\mathrm{D}}\left(q\right)$ (circles) and ${\gamma }_{\mathrm{O}\mathrm{D}}\left(q\right)$ (lines) computed from the KMCs for different lag times $\mathrm{\Delta }t$; a number of points are noteworthy. 1) We find no significant deviations between the friction profiles extracted from MD (solid lines and filled circles) and GLE (broken lines and open circles) trajectories; this reverberates that the GLE describes the protein dynamics very faithfully. 2) The underdamped and overdamped friction profiles ${\gamma }_{\mathrm{U}\mathrm{D}}\left(q\right)$ and ${\gamma }_{\mathrm{O}\mathrm{D}}\left(q\right)$ disagree for all lag times $\mathrm{\Delta }t$, which very clearly demonstrates an inconsistency in the Markovian description of protein folding. In fact, in the limit $\mathrm{\Delta }t\to 0$, both $D_{qq}$ and $D_{vv}$ vanish; thus, ${\gamma }_{\mathrm{O}\mathrm{D}}\left(q\right)$ diverges, while ${\gamma }_{\mathrm{U}\mathrm{D}}\left(q\right)$ goes to zero (SI Appendix, section 12). 3) While the underdamped friction ${\gamma }_{\mathrm{U}\mathrm{D}}\left(q\right)$ never reaches a realistic value close to $\overline{\gamma }$, the overdamped friction ${\gamma }_{\mathrm{O}\mathrm{D}}\left(q\right)$ approaches $\overline{\gamma }$ for $\mathrm{\Delta }t\approx 1$ ns. This shows that lag times of the order of the longest memory time have to be used in order to generate realistic friction values. 4) The friction profiles extracted from the GLE simulations are position dependent, seen most clearly in ${\gamma }_{\mathrm{O}\mathrm{D}}\left(q\right)$ for $\mathrm{\Delta }t=1\hspace{0.17em}$ ns (purple broken line); this is clearly a spurious effect since the GLE has no position-dependent friction. We conclude that the mapping of a non-Markovian process onto a Markovian LE produces spurious position-dependent friction effects. Presumably, the effective friction of proteins will in general exhibit a dependence on the reaction coordinate, but the extraction of friction profiles would have to account for memory effects in order to avoid spurious effects. The capability of the GLE Eq. 1 to very accurately reproduce the MD simulation kinetics suggests that for the present case of ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$, the spatial dependence of friction is negligible.

Fig. 4.

(A) Friction coefficient profiles $\gamma \left(q\right)$ from KMC analysis for different lag times $\mathrm{\Delta }t$ (different colors) for the underdamped (underd.) Langevin model, Eq. 8, from MD (filled circles) and GLE simulations (open circles) and for the overdamped (overd.) Langevin model, Eq. 9, from MD (solid lines) and GLE simulations (broken lines). The gray horizontal line shows the total friction coefficient $\overline{\gamma }$ extracted from MD simulations. (B) Friction profiles computed from the MD MFPT profiles in Fig. 3A using Eq. 11. ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q_F\right)$ follows from the unfolding MFPTs for start position $q_S=0.32\hspace{0.17em}$ nm, and ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q_F\right)$ follows from folding MFPTs for $q_S=0.99\hspace{0.17em}$ nm. The gray horizontal line denotes the friction coefficient $\overline{\gamma }$ extracted from MD simulations. The gray curve in the background shows the folding free energy $U\left(q\right)$. (C) MFPTs from MD and GLE simulations are compared with overd. Markovian predictions according to Eq. 10 using ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q_F\right)$ and ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q_F\right)$ from B.

An alternative way to determine a friction profile $\gamma \left(q\right)$ in the overdamped limit uses the one-to-one relation between the MFPT profiles in Fig. 3A and $\gamma \left(q\right)$. From the expressions for the folding and unfolding times (Eq. 10), $\gamma \left(q\right)$ follows by inversion according to Eq. 11 (30). In Fig. 4B, we show ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q_F\right)$ and ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q_F\right)$ computed from unfolding and folding MFPTs from MD simulations for start positions $q_S=q_L$ and $q_S=q_R$, respectively. Not surprisingly, the profiles ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q_F\right)$ and ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q_F\right)$ are rather close to $\overline{\gamma }$ extracted from the MD simulations, which is shown as a gray horizontal line in Fig. 4B, but differ significantly from each other. This suggests that a single friction profile cannot describe folding and unfolding of ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ simultaneously. In fact, the values of ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q_F\right)$ and ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q_F\right)$ go down as $q_F$ moves to the respective start positions (i.e., as the folding and unfolding times become shorter). This reflects that memory effects particularly accelerate fast transitions (36–38).

To demonstrate the limitations of the friction profiles in Fig. 4B, we show in Fig. 4C folding and unfolding MFPT profiles that are calculated according to Eq. 10 from ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q\right)$ (filled circles) and ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q\right)$ (open circles). By construction, the MFPTs using ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q\right)$ reproduce the unfolding simulation data, while the MFPTs using ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q\right)$ reproduce the folding simulation data. In contrast, the MFPTs using ${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q\right)$ fail to reproduce the simulated folding times, and the MFPTs using ${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q\right)$ fail to reproduce the simulated unfolding times, in particular when the folding/unfolding times become smaller than about 10 ns. In contrast, the GLE model (broken lines) reproduces both folding and unfolding MD dynamics (solid lines). This underlines that there is no consistent way of describing the complete folding/unfolding dynamics with a Markovian model.

Conclusions

By extracting the time-dependent friction from MD simulations for the polypeptide ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ from explicit-water MD simulations, we demonstrate that the resulting GLE model can be straightforwardly integrated numerically and reproduces the folding and unfolding kinetics of the MD simulations very accurately. Our findings are not restricted to a reaction coordinate based on the summed distances between native H bonds. As we show in SI Appendix, section 7, the same analysis of the Ala9 end-to-end distance leads to similar results. Decreasing the memory time in the GLE while keeping the friction coefficient (i.e., the integral over the memory function) constant, the folding kinetics changes significantly for folding and unfolding events. This shows that memory effects are important even for the formation kinetics of a single $\alpha$-helix.

In contrast, the Markovian LE cannot reproduce the full ${\mathrm{A}\mathrm{l}\mathrm{a}}_9$ reconfiguration dynamics, even with a fitted friction profile; this follows from the comparison of the folding and unfolding kinetics, which would need to be modeled with different friction profiles in order to reproduce the MD simulation kinetics.

We have mostly used the GLE model as a diagnostic tool to understand and quantify non-Markovian effects; since non-Markovian simulations are rather inexpensive, they can also be used as an efficient tool to simulate the response of proteins to environmental changes (e.g., externally applied forces). In fact, our extraction technique for the memory function can in principle also be applied to trajectories from single-molecule experiments (13–15), which would enable us to perform non-Markovian GLE simulations on experimental systems directly, without the need of atomistic MD simulations. Because of the limited time resolution of typical experimental data, suitable extraction techniques would have to be used (24, 46).

Methods

MD and GLE Simulation Details.

We use the all-atom Amber03 force field (47) with extended simple point-charge (SPC/E) water (48). The cubic simulation box has side lengths of $4.95\hspace{0.17em}$ nm and contains 4,023 water molecules. The Lennard–Jones interactions are cut off after $1.0\hspace{0.17em}$ nm. For long-range electrostatic interactions, we use the particle Mesh Ewald method (49). The simulation time step is 1 fs, and the total simulation time is $10\hspace{0.17em}\mathrm{\mu }$s. All simulations are performed in the NVT ensemble using the Gromacs 2019 MD package (50). Further details are given in SI Appendix, section 1. In the GLE simulations, we used the same time step and simulation time as in the MD simulations. Input files of the MD simulations are available for download under (http://dx.doi.org/10.17169/refubium-29935). Our Python scripts for the numerical extraction of the memory kernel, for performing a GLE simulation, and computing MFPTs can be found in GitHub (https://github.com/lucastepper/memtools).

From MFPTs to Friction Profiles.

The MFPT is defined as the mean time needed to reach the final position $q_F$ for the first time when starting from a position $q_S$. For the overdamped LE in Eq. 5, it reads for $q_S<q_F$ (51),

$${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_S,q_F\right)=\beta {\int }_{q_S}^{q_F}\mathrm{d}q\hspace{0.17em}{e}^{\beta U\left(q\right)}\gamma \left(q\right){\int }_{q_{min}}^q\mathrm{d}{q}^{\prime }\hspace{0.17em}{e}^{-\beta U\left(q^{\prime }\right)}$$ [10a]

and for $q_S>q_F$,

$${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}\left(q_S,q_F\right)=\beta {\int }_{q_F}^{q_S}\mathrm{d}q\hspace{0.17em}{e}^{\beta U\left(q\right)}\gamma \left(q\right){\int }_q^{q_{max}}\mathrm{d}{q}^{\prime }\hspace{0.17em}{e}^{-\beta U\left(q^{\prime }\right)}.$$ [10b]

Taking the derivative of Eq. 10 w.r.t. $q_F$ gives the friction profile $\gamma \left(q_F\right)$ as (30)

$${\gamma }_{\mathrm{u}\mathrm{n}\mathrm{f}}\left(q_F\right)=k_{B}T\hspace{0.17em}\frac{e^{-\beta U\left(q_F\right)}}{Z_1}\frac{\partial {\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}}{\partial q_F}\text{for}{q}_S<q_F,$$ [11a]

$${\gamma }_{\mathrm{f}\mathrm{o}\mathrm{l}}\left(q_F\right)=-k_{B}T\hspace{0.17em}\frac{e^{-\beta U\left(q_f\right)}}{Z_2}\frac{\partial {\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}\mathrm{T}}}{\partial q_F}\text{for}{q}_S>q_F,$$ [11b]

where $Z_1={\int }_{q_{min}}^{q_F}\mathrm{d}q\hspace{0.17em}{e}^{-\beta U\left(q\right)}$ and $Z_2={\int }_{q_F}^{q_{max}}\mathrm{d}q\hspace{0.17em}{e}^{-\beta U\left(q\right)}$.

Data Availability

Derivations that support the findings of this study are included in SI Appendix. Simulation input files data have been deposited in Institutional Repository (http://dx.doi.org/10.17169/refubium-29935). Our codes for extracting the memory kernel, running GLE simulations, and for computing MFPTs are available in GitHub (https://github.com/lucastepper/memtools).