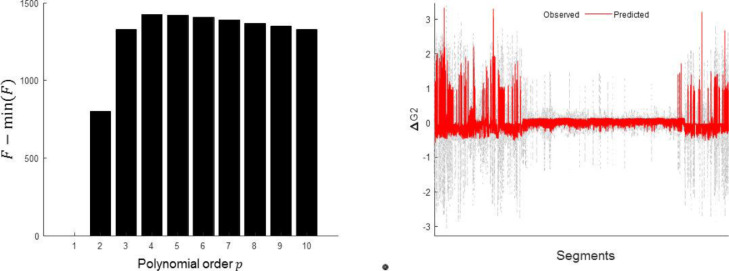
Fig. 6.

Modelling the evolution of parameter ($\Delta {\mathit{G}}_2$) with respect to empirical frequency content in the data. a) This panel shows relative free energy (with respect to the smallest model evidence) of the second level GLM. We estimated the model evidence associated with models of changes in synaptic parameters based on a linear-in-coefficients polynomial of the empirical frequency content of the ensuing neuronal responses – as captured by the data (Eq. 6). Here the optimal power of the polynomial is 4. b) Observed and predicted model of the parameter dynamic ($\Delta {\mathit{G}}_2$) with polynomial order 4 in Eq. 6. In this and all subsequent figures, changes in the parameters are expressed in terms of log scaling. In other words, a value of 0 corresponds to a scaling by exp(0)=1. For small changes, the log scaling is roughly equal to the proportional change (i.e., -.1 is roughly a decrease of 10%). The free energy of a model with order 4 was 30674 and for order 5 was 30557 < 30674. By converting these log evidence approximations to the posterior probability of each model (which by Bayes rule under equal priors is a softmax function), we would select the model order of 4, which has posterior probability approaching 100%.