Plasma Turbulence at Comet 67P/Churyumov-Gerasimenko: Rosetta Observations

Abstract

We perform a power spectral analysis of magnetic field fluctuations measured by the Rosetta spacecraft’s magnetometer at comet 67P/Churyumov-Gerasimenko. We interpret the power spectral signatures in terms of plasma turbulent processes and discover that different turbulent processes are prominent during different active phases of the comet. During the weakly active phase of the comet, dominant injection is prominent at low frequencies near 10⁻² Hz, while partial energy cascade or dispersion is prominent at high frequencies near 10⁻¹ Hz. During the intermediately active phase, uniform injection is prominent at low frequencies, while partial energy cascade or dispersion is prominent at high frequencies. During the strongly active phase of the comet, we find that partial energy cascade or dissipation is dominant at low frequencies, while partial energy cascade, dissipation, or dispersion is dominant at high frequencies. We infer that the temporal variations of the turbulent processes occur due to the evolution of the plasma environment of the comet as it orbits the Sun.

1. Introduction

1.1. Turbulence

Turbulence refers to fluctuations and nonlinear interactions that occur among these fluctuations in fluids, gases, and plasmas (Bruno & Carbone, 2016). Investigation of turbulence enables tracking of the evolution of energy in fluid, gas, or plasma systems from its injection to its dissipation. In a fluid, for example, energy injected at large spatial scales first undergoes an energy cascade in which the energy is transferred to successively smaller spatial scales (Kolmogorov, 1941). Then, when the energy reaches spatial scales that are comparable to viscous spatial scales of the fluid, the energy is ultimately dissipated.

Solar wind plasma and plasmas in planetary and lunar environments behave analogously to fluids, exhibiting turbulent processes such as energy injection, energy cascade, and dissipation. The power spectra of magnetic field fluctuations in these plasmas exhibit different slopes or spectral indices in different frequency ranges, which indicates the existence of these different turbulent processes in different frequency ranges (Alexandrova et al., 2008, 2012; Bruno & Carbone, 2016; Cattaneo et al., 2000; Coleman, 1968; Dwivedi et al., 2015; Glassmeier, 1995; Goldstein et al., 1995; Hadid et al., 2015; Kiyani et al., 2009, 2015; Leamon, Matthaeus, et al., 1998; Leamon, Smith, et al., 1998; Luo et al., 2016; Matthaeus & Goldstein, 1986; Matthaeus et al., 1994; Roberts et al., 2013, 2015; Ruhunusiri et al., 2017; Sahraoui et al., 2006, 2009, 2010, 2013; Saur et al., 2002; Tao et al., 2015; TenBarge et al., 2013; Tu & Marsch, 1995; Uritsky et al., 2011; von Papen et al., 2014; Vörös, Zhang, Leaner, et al., 2008; Vörös, Zhang, Leubner, et al., 2008; Zimbardo et al., 2010). For example, in the solar wind at 1 AU (astronomical unit), the magnetic field power spectrum has spectral indices near −1 and −5/3 for frequencies below 10⁻⁴ Hz and for frequencies between 10⁻⁴ and 0.1 Hz. Thus, energy injection or containment is interpreted to occur for frequencies below 10⁻⁴ Hz (Bruno & Carbone, 2016; Goldstein et al., 1995; Kiyani et al., 2015; Matthaeus & Goldstein, 1986; Matthaeus et al., 1994; Tu & Marsch, 1995), and energy cascade is interpreted to occur for frequencies between 10⁻⁴ and 0.1 Hz (Bruno & Carbone, 2016; Coleman, 1968; Goldstein et al., 1995; Kiyani et al., 2015; Tu & Marsch, 1995) in the solar wind at 1 AU.

The Rosetta mission enabled for the first time a long-term characterization of turbulence at a comet. Plasma turbulence has been previously studied at four comets: 21P/Giacobini-Zinner (Tsurutani & Smith, 1986; Tsurutani et al., 1995), 1P/Halley (Glassmeier et al., 1989; Neubauer et al., 1986; Tsurutani et al., 1995; Yumoto et al., 1986), 26P/Grigg-Skjellerup (Glassmeier & Neubauer, 1993; Tsurutani et al., 1995), and 19P/Borrelly (Richter et al., 2011). Since these studies are all based on flyby missions, determining if and how turbulent processes vary spatially and temporally as these comets orbited around the Sun was not possible. The Rosetta spacecraft, on the other hand, made comprehensive in situ measurements in the plasma environment of comet 67P/Churyumov-Gerasimenko for nearly 2 years (from August 2014 to September 2016), covering a large spatial region surrounding the comet as it orbited the Sun. The 2-year observation period was centered on the comet’s perihelion which occurred on August 2015. During this time, the comet’s heliocentric distance varied in the range from ~4 to ~1.3 AU. Thus, Rosetta measurements are ideal for determining if and how turbulent processes vary at a comet temporally and spatially as it orbits the Sun, and this will be the objective of our paper.

1.2. The Plasma Environment of Comet 67P

The plasma environment of a comet changes as it orbits the Sun. A comet is composed of frozen volatiles and dust, and their sublimation leads to a loss of neutral cometary material to space, usually water and carbon dioxide. These neutrals become photoionized by Sun’s extreme ultraviolet radiation (Mendis & Ip, 1976). As the comet orbits the sun, its outgassing rate can increase, leading to a change in the interaction between solar wind plasma and the cometary plasma.

Based on the outgassing rate of a comet, it can have three active phases: weak, intermediate, and strong (Götz et al., 2019). Farther from the sun, when the outgassing rate Q is low (or Q < 5 × 10²⁶ molecules/s), the comet is weakly active. During this phase, the deflection and deceleration of solar wind ions are expected to be small (see Figure 1a). When the heliocentric distance decreases, and when 5 × 10²⁶ < Q < 5 × 10²⁷ molecules/s, the comet enters the intermediately active phase. At this phase, the solar wind ions can be significantly decelerated and deflected by the cometary ions due to mass loading (Neubauer, 1988), forming a solar wind ion cavity near the comet that is devoid of solar wind ions (see Figure 1b). The interplanetary magnetic field also drapes around the comet and piles up in the comet’s sunward-facing side (Israelevich & Ershkovich, 1994). Near perihelion, when the outgassing rate becomes maximum and if Q > 5 × 10²⁷ molecules/s, the comet becomes strongly active. During this phase, a diamagnetic cavity can form surrounding the comet (Neubauer et al., 1986), downstream of the solar wind ion cavity (see Figure 1c). The diamagnetic cavity is a magnetic field-free region. During this strongly active phase of the comet, a well-developed bow shock can form farther upstream from the solar wind ion cavity (Götz et al., 2019).

Figure 1.

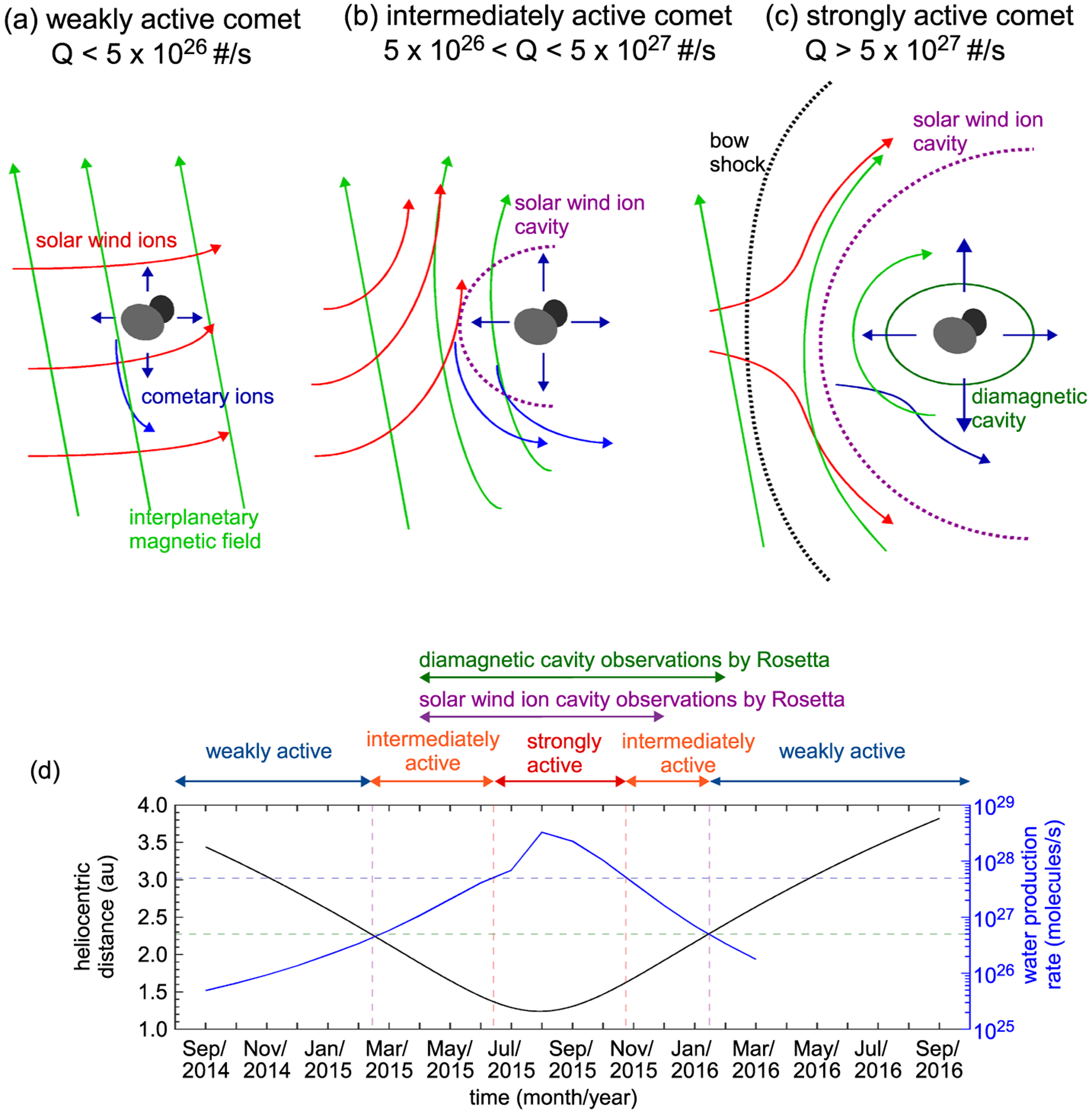
The plasma environment of a comet as it transitions from a weakly active comet to a strongly active comet is shown in (a–c). This figure is based on Figure 1.1 of Götz et al. (2019). Heliocentric distance of comet 67P from September 2014 to September 2016 is shown in (d). The empirical fits for water production rate Q determined by Hansen et al. (2016) are also shown in (d).

Water production rates measured at comet 67P indicate that it underwent all the three active phases discussed above (Götz et al., 2019; Hansen et al., 2016). In Figure 1d, we plot the heliocentric distance variation for comet 67P from September 2014 to September 2016, which will be our analysis period, along with the empirical fits for the water production rate at comet 67P determined by Hansen et al. (2016) based on the measurements made by Rosetta and earth-based observations. We have marked in Figure 1d the time intervals that we expect to observe the weakly, intermediately, and strongly active phases of the comet based on the outgassing rates as described above.

Water ion pickup or acceleration by solar wind convective electric field was observed at comet 67P (Goldstein et al., 2015; Nilsson, Wieser, Behar, Wedlund, Kallio, et al., 2015). Conservation of momentum leads to the deflection of solar wind opposite to the solar wind convection electric field. This was indeed observed at comet 67P, and the deflection was found to increase with decreasing heliocentric distances, with deflections reaching as large as 90° near 2 AU (Behar, Lindkvist, et al., 2016; Behar, Nilsson, et al., 2016; Broiles et al., 2015). Rosetta observed a solar wind ion cavity almost continuously from April 2015 to December 2015 (Behar et al., 2017; Nilsson et al., 2017). Magnetic field pileup and draping were observed at comet 67P (Koenders et al., 2016; Nilsson, Wieser, Behar, Wedlund, Gunell, et al., 2015; Volwerk et al., 2017, 2019). Rosetta also observed a diamagnetic cavity, frequently (about 600 times) from April 2015 to February 2016 (Goetz et al., 2016). So the diamagnetic cavity at comet 67P was present during the comet’s intermediately active phase as well. A bow shock in its infant phase of development was observed at a distance of 80 km from the comet when the heliocentric distance was near 2 AU, and it was estimated that the bow shock would have been located at least 4,000 km upstream of the comet during perihelion (Gunell et al., 2018).

Rosetta also observed several plasma dynamical processes, including low-frequency waves (frequently referred to as “the singing of the comet” in the literature) in the frequency range from 10 to 100 mHz, which were prominently observed upon the spacecraft’s arrival at the comet prior to perihelion. These waves were interpreted to be excited by an ion Weibel instability (Breuillard et al., 2019; Glassmeier, 2017; Richter et al., 2015, 2016). Near perihelion, these waves were not observed. Instead, large-amplitude chaotic magnetic field fluctuations were observed (Glassmeier, 2017). Six months after the perihelion, near February 2016, the low-frequency waves were observed to reappear (Glassmeier, 2017).

The nominal plasma parameters at comet 67P during the weakly active phase, within the solar wind ion cavity, and the diamagnetic cavity observed during the intermediately active and strongly active phases of the comet estimated based on Rosetta observations are summarized in Table 1. These parameters will be useful to interpret our observations as described in the next section.

Table 1.

Nominal Plasma Parameters at Comet 67P

Parameter	Weakly active phase	Intermediately/strongly active phase Solar wind ion cavity	Diamagnetic cavity
np (cm−3)	1–2a	~0b	~0c
Vp (km/s)	300–600d	~0b	~0c
nH 2O+ (cm−3)	50–200 (near comet)e	50–400f	100–1,500g
V H 2O+ (km/s)	30–60 (near comet/mainly antisunward)d	10–40 (mostly antisunward)f	2–4 (mostly radially outward from comet)h
B (nT)	10–24	20–37	<1c
f di (Hz)	1.3–3.7 0.2–0.9 (near comet)	0.07–0.8	0.02–0.2

Note. Here, n_p is the proton density, V_p is the proton speed, n_{H 2O+} is the H₂O⁺ ion density, V_{H 2O+} is the H₂O⁺ ion velocity, B is the magnetic field magnitude, and f _di is the ion inertial frequency.

^aMeier et al. (2016).

^bBehar et al. (2017).

^cGoetz et al. (2016).

^dNilsson, Wieser, Behar, Wedlund, Kallio, et al. (2015).

^eGunell et al. (2017).

^fVolwerk et al. (2016).

^gHenri et al. (2017).

^hOdelstad et al. (2018).

2. Identification of Turbulent Processes at Comet 67P

We interpret turbulent processes by determining the spectral indices of the magnetic field power spectra. For this determination, we analyzed Rosetta’s 20-Hz outboard magnetometer data (Glassmeier et al., 2007).

Our analysis procedure is as follows. First, we fast Fourier transformed each of the three mutually perpendicular components of the magnetic field by selecting an 820-s time segment. This step yielded the power of fluctuations for each of the components, as a function of frequency. Then, we summed the power of these three components to obtain the total power spectra of the magnetic field fluctuations. Six examples of magnetic field power spectra computed in this manner are shown in Figure 2.

Figure 2.

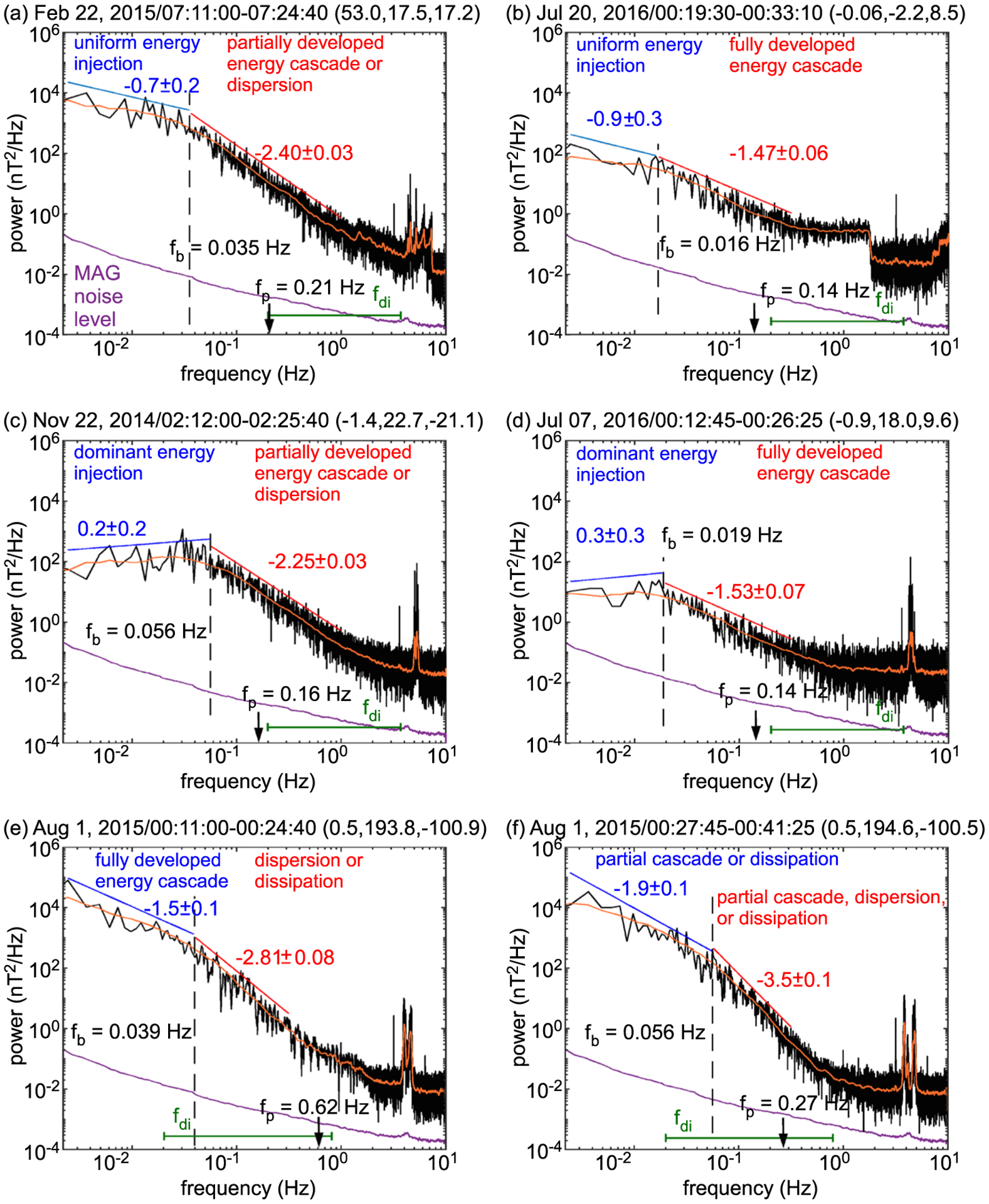
Six different power spectra of magnetic field fluctuations observed at comet 67P, which depict six different combinations of turbulent processes, are shown in (a–f). The frequency at which a sharp transition of the spectral indices occurs is indicated by f b, which is the spectral break frequency. The local proton gyrofrequency is indicated by f p. The time interval associated with each power spectrum is provided above each panel. The mean solar equatorial frame (CSEQ) coordinates for the spacecraft are also provided in kilometers, within brackets above each panel.

As can be seen in the power spectra in Figure 2, the selection of 820-s time windows enabled us to obtain magnetic field power fluctuation information over a broad frequency range from 0.002 (corresponds to two wavelengths that fit the 820-s time window) to 10 Hz (corresponds to the Nyquist frequency for 20-Hz data), which enabled us to identify turbulent processes over a broad range of frequencies. Large spectral peaks can be seen near 5 Hz in these power spectra. These are artifacts due to the spacecraft reaction wheels. The spectra also flatten in this high-frequency range due to the magnetometer reaching its noise floor.

The power spectra shown in Figure 2 can generally be divided into two separate ranges with different spectral indices: a low-frequency range with a higher value of the spectral index (or a less-steep slope) and a high-frequency range with a lower value of the spectral index (or a more-steep slope). This indicates that the turbulent processes in the low-frequency range are generally different from those in the high-frequency range.

Now, we will discuss how spectral indices of magnetic field power spectra can be used to interpret the underlying turbulent processes. Spectral indices near −1 indicate energy injection via multiple sources leading to excitation of uncorrelated waves over a broad range of frequencies (Bruno & Carbone, 2016; Goldstein et al., 1995; Kiyani et al., 2015; Matthaeus & Goldstein, 1986; Ruhunusiri et al., 2017; Tu & Marsch, 1995; Uritsky et al., 2011; Vörös, Zhang, Leubner, et al., 2008). Henceforth, we will refer to this scenario as uniform energy injection. In Figures 2a and 2b, for low frequencies (near 10⁻² Hz), the spectral indices are near −1, which indicates uniform energy injection at low frequencies. Here we note that a spectral index of −1 does not necessarily indicate that active energy injection is occurring at the time of the observation. The active energy injection could have occurred prior to the observation time.

Positive values or low negative numbers of spectral indices indicate the presence of a dominant energy injection mechanism confined to a certain frequency range (Ruhunusiri et al., 2017; Uritsky et al., 2011). In Figures 2c and 2d, the spectral indices at low frequencies (near 10⁻² Hz) have positive values. The power spectra shown in Figures 2c and 2d are peaked near 0.06 and 0.02, respectively. Richter et al. (2015, 2016) reported an observation of low-frequency waves in the frequency range from 0.01 to 0.10 Hz, which were attributed to excitation by an ion Weibel instability. Since the frequencies for the peaks in Figures 2c and 2d fall within the 0.01 to 0.10 Hz range, it is possible that these peaks correspond to waves excited by the aforementioned ion Weibel instability.

Spectral indices near −1.6 (the Kolmogorov value) are consistent with the presence of fully developed energy cascade (Bruno & Carbone, 2016; Coleman, 1968; Goldstein et al., 1995; Kiyani et al., 2015; Matthaeus et al., 1994; Ruhunusiri et al., 2017; Tu & Marsch, 1995; Tsurutani & Smith, 1986) in which the energy is transferred from low frequencies to high frequencies via a nonlinear interaction among waves. In Figures 2b and 2d, in the high-frequency range (near 10⁻¹ Hz), the spectral indices are near the Kolmogorov value. Thus, Figures 2b and 2d depict two examples at comet 67P, where the spectral indices indicate the presence of fully developed energy cascade at high frequencies. In Figure 2e, the low-frequency spectral index has a value near the Kolmogorov value. Thus, Figure 2e is an example where the spectral index is indicative of the presence of fully developed energy cascade at low frequencies.

Spectral indices steeper than the Kolmogorov value indicate the presence of either partially developed energy cascade (Ruhunusiri et al., 2017; Tsurutani & Smith, 1986), dissipation (Kiyani et al., 2009, 2015; Leamon, Matthaeus, et al., 1998; Leamon, Smith, et al., 1998; Ruhunusiri et al., 2017; TenBarge et al., 2013; Tsurutani & Smith, 1986), or dispersion due to Hall effects (Galtier, 2006; Galtier & Buchlin, 2007; Ghosh et al., 1996; Krishan & Mahajan, 2004; Stawicki et al., 2001). Figures 2a, 2c, 2e, and 2f have spectral indices steeper than the Kolmogorov value in the high-frequency range, and Figure 2f has spectral indices steeper than the Kolmogorov value in the low-frequency range. So, based on only the spectral index values, partially developed energy cascade, dissipation, and dispersion are all possibilities for physical processes that can occur in the high-frequency range in Figures 2a, 2c, 2e, and 2f and the low-frequency range in Figure 2f. Below, we will discuss whether we can confirm the existence of these possibilities or eliminate some of them by determining which kinetic physics is significant or possible for the different frequency ranges.

Dispersion is inferred to be significant for length scales less than the ion inertial length d_i but greater than the electron inertial length as Hall effects are significant for these length scales (Huba, 2003). The ion inertial length $d_i=m_i^{\left(1/2\right)}/{\left(n_i{q}_i^2{\mu }_o\right)}^{\left(1/2\right)}$, where m_i is the mass of the ion, n_i is the ion density, q_i is the ion charge, and μ₀ is the magnetic permeability of vacuum. The frequency equivalent of d_i is f _di = V_bulk/d_i, where V_bulk is the bulk ion speed, and Hall effects should be important for frequencies higher than f _di.

Determining d_i or f _di requires knowledge of ion moments at comet 67P. While the Rosetta spacecraft had instruments for determining ion moments such as the ion and electron sensor, the bulk of the distribution is inferred to fall outside the field of view for a majority of times. Thus, high accuracy ion moments are not available for the majority of times at comet 67P, and we cannot determine the frequencies corresponding to the ion inertial length for each of the spectra shown in Figure 2. Therefore, we use the nominal values of plasma parameters in Table 1 (which are determined in previous literature mainly from observations when there are minimal field of view issues or by long-term averaging) to compute f _di, and these are tabulated in the last row of Table 1. Since based on Figure 1d, we know the most probable environment in which Rosetta was in for each month, we can infer the most probable range for f _di for each spectrum shown in Figure 2. So, from September 2014 to February 2015 and from February 2016 to September 2016, 0.2 < f _di < 3.7 Hz, and from March 2015 to January 2016, 0.02 < f _di < 0.8 Hz. These estimated f _di coincide with the high-frequency range in our power spectra. Thus, dispersion should be a possibility for a process that can occur in the high-frequency ranges in Figures 2a, 2c, 2e, and 2f. The estimated f _di does not coincide with the low-frequency range in our power spectra. Thus, dispersion should not be a possible process that can occur in the low-frequency range in Figure 2f.

A partially developed energy cascade means that waves, which are excited at low frequencies, do not have sufficient time to nonlinearly interact with one another. Thus, the fully developed energy cascade is not achieved. Now we will determine whether there is a way to eliminate either partially developed energy cascade or dissipation when the spectral index alone indicates that both are possibilities for turbulent processes that can occur in a certain frequency range. In Figures 2a and 2c, the high-frequency spectral indices indicate the presence of either partially developed energy cascade or dissipation in the high-frequency range. However, as inferred earlier, the physical process operating in the low-frequency range is energy injection. According to the phenomenology of turbulence, energy transfers to smaller scales or higher frequencies while evolving from energy injection, through cascade to eventual dissipation. Thus, energy cascade, not dissipation, should be observed for higher frequencies immediately adjacent to the energy injection frequencies (Goldstein et al., 1995). Using this argument for Figures 2a and 2c, we can eliminate dissipation from the possible turbulent process that can occur in the high-frequency ranges in those spectra. So, Figure 2a is an example where uniform injection occurs in the low frequencies and either partially developed energy cascade or dispersion occurs in the high frequencies. Figure 2c is an example where dominant injection occurs in the low frequencies and either partially developed energy cascade or dispersion occurs in the high frequencies.

Now, we consider Figure 2e. Above, we determined that the physical process operating in the low-frequency range is fully developed energy cascade. Since, according to the phenomenology of turbulence, dissipation should be observed for higher frequencies immediately adjacent to the frequencies where fully developed energy cascade is present, the process present in the high-frequency range in Figure 2e should be dissipation and not partial cascade. Thus, Figure 2e is an example where fully developed energy cascade occurs for low frequencies, while either dissipation or dispersion occurs for high frequencies.

To determine which turbulent processes are prominent at comet 67P, we classified ranges of spectral indices that can be associated with various turbulent processes (see Table 2). Within the frequency range in the solar wind that is associated with the fully developed energy cascade, spectral indices typically have values in the range from −1.4 to −1.7 (Podesta, 2011). Thus, we associate spectral indices in that range with the fully developed energy cascade. Since spectral indices closer to −1 indicate uniform energy injection as discussed above, and since −1.4 is selected as the upper limit of the fully developed energy cascade, and low negative values can indicate dominant injection, spectral indices between −1.4 and −0.5 are associated with uniform injection. Since −0.5 is selected as the upper limit for uniform injection, spectral index values ≥ − 0.5 are associated with dominant injection. We associate spectral index values <−1.7 with partial cascade, dissipation, and dispersion as −1.7 is selected as the lower limit for fully developed energy cascade. In Table 2, we outline eight possible combinations of turbulent processes that can occur concurrently in the low- and high-frequency ranges. For brevity, we will use TP1 through TP8 designations to refer to these eight combinations of turbulent processes in the remainder of the paper.

Table 2.

Classification of Turbulent Processes Based on Spectral Indices

Turbulent process designator	Low-frequency turbulent processes and spectral index range	High-frequency turbulent processes and spectral index range
TP1	Dominant energy injection	Partial cascade or dispersion
	sl ≥ −0.5	sh < −1.7
TP2	Uniform energy injection	Partial cascade or dispersion
	−0.5>sl > −1.4	sh < −1.7
TP3	Partial cascade or dissipation	Partial cascade, dissipation, or dispersion
	sl < −1.7	sh < −1.7
TP4	Fully developed energy cascade	Dissipation or dispersion
	−1.4 ≥ sl ≥ −1.7	sh < −1.7
TP5	Dominant energy injection	Fully developed energy cascade
	sl ≥ −0.5	−1.4 ≥ sh ≥ −1.7
TP6	Uniform energy injection	Fully developed energy cascade
	−0.5>sl > −1.4	−1.4 ≥ sh ≥ −1.7
TP7	Dominant or uniform energy injection	Dominant or uniform energy injection
	sl > −1.4	sh > −1.4
TP8	Fully developed energy cascade	Fully developed energy cascade
	−1.4 ≥ sl ≥ −1.7	−1.4 ≥ sh ≥ −1.7

Note. Here, s_l and s_h refer to the low- and high-frequency spectral indices, respectively.

3. Spectral Break Frequency and Spectral Indices Determination

To determine low- and high- frequency spectral indices, we first computed the magnetic field power spectra using a sliding 820-s time window that was shifted each time by 30 s for the entire time frame from September 2014 to September 2016. We smoothed each power spectra (as shown in Figure 3a) between 10^−2.7 to 1 Hz. Frequencies above 1 Hz were not included in this analysis to avoid any misinterpretations due to the reaction wheel artifacts often seen for frequencies >1 Hz (see Figure 2). Then, centered on four frequencies within 10^−2.5 to 1 Hz that have the same log frequency separation of 0.5, we fitted two straight lines to the smoothed power spectrum in the low-frequency side and the high-frequency side. Then, using the gradients and intercepts of the two straight lines, we computed the frequency at which they would intersect and computed the difference between this intercept frequency and the frequency that we selected to fit the two straight lines to the power spectrum. At the spectral break frequency, this difference should be a global minimum, and we found a coarse value for the spectral break frequency by finding the frequency at which this difference became a global minimum (see Figure 3b). Then, centered on the coarse frequency in which the frequency difference was found to be a global minimum, we performed a second iteration of the two-line fitting procedure for finer frequency increments for a log frequency interval of 1 (see Figure 3c). Then, we found the frequency at which the frequency difference became a global minimum for this second iteration and used that as the spectral break frequency. Then, fitting a straight line between 10^−2.7 Hz and the spectral break frequency to the original or the unsmoothed spectrum, we determined the low-frequency spectral index along with its uncertainty. High-frequency spectral index and its uncertainty were determined by fitting a straight line to the original spectrum between the spectral break frequency and 1 Hz. The uncertainties of spectral indices were determined using equation 4.31 of Squires (1999).

Figure 3.

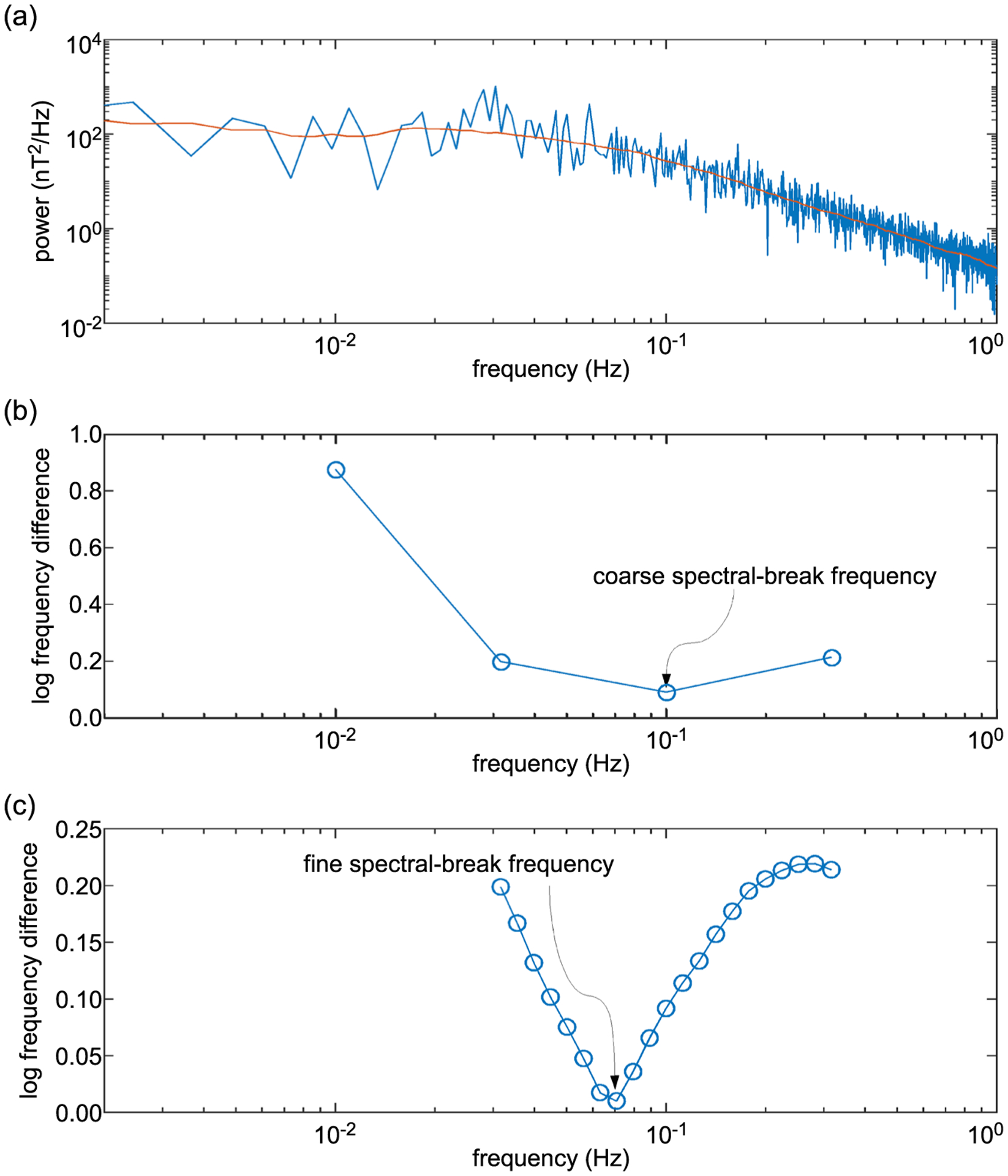
Procedure for determining the spectral break frequency for a power spectrum is depicted in (a–c).

The median spectral break frequencies for each month from September 2014 to September 2016 are shown in Figure 4a with their quartiles. As can be seen in Figure 4a, the spectral break frequencies are lower during the intermediately active and strongly active phases of the comet than during the weakly active phase of the comet. The medians for low- and high-frequency spectral indices determined for each month from September 2014 to September 2016 are shown in Figure 4b. The low- and high-frequency spectral indices are steeper during the intermediately active and strongly active phases of the comet than during the weakly active phase of the comet.

Figure 4.

Median spectral break frequencies and median low- and high-frequency spectral indices for each month with their quartiles are shown in (a) and (b).

4. Temporal Variations of Turbulent Processes

In Figures 5 and 6, we depict the occurrence rates for the eight possible combinations of turbulent processes for each month with their uncertainties. We find that different turbulent processes became prominent during the different active phases of the comet. In particular, the turbulent process interpreted to be either dominant injection-partial cascade or dominant injection-dispersion (TP1) had the highest occurrence rate during the weakly active phase of the comet, whereas its occurrence rate became negligible during the intermediately and strongly active phases of the comet (see Figure 5a).

Figure 5.

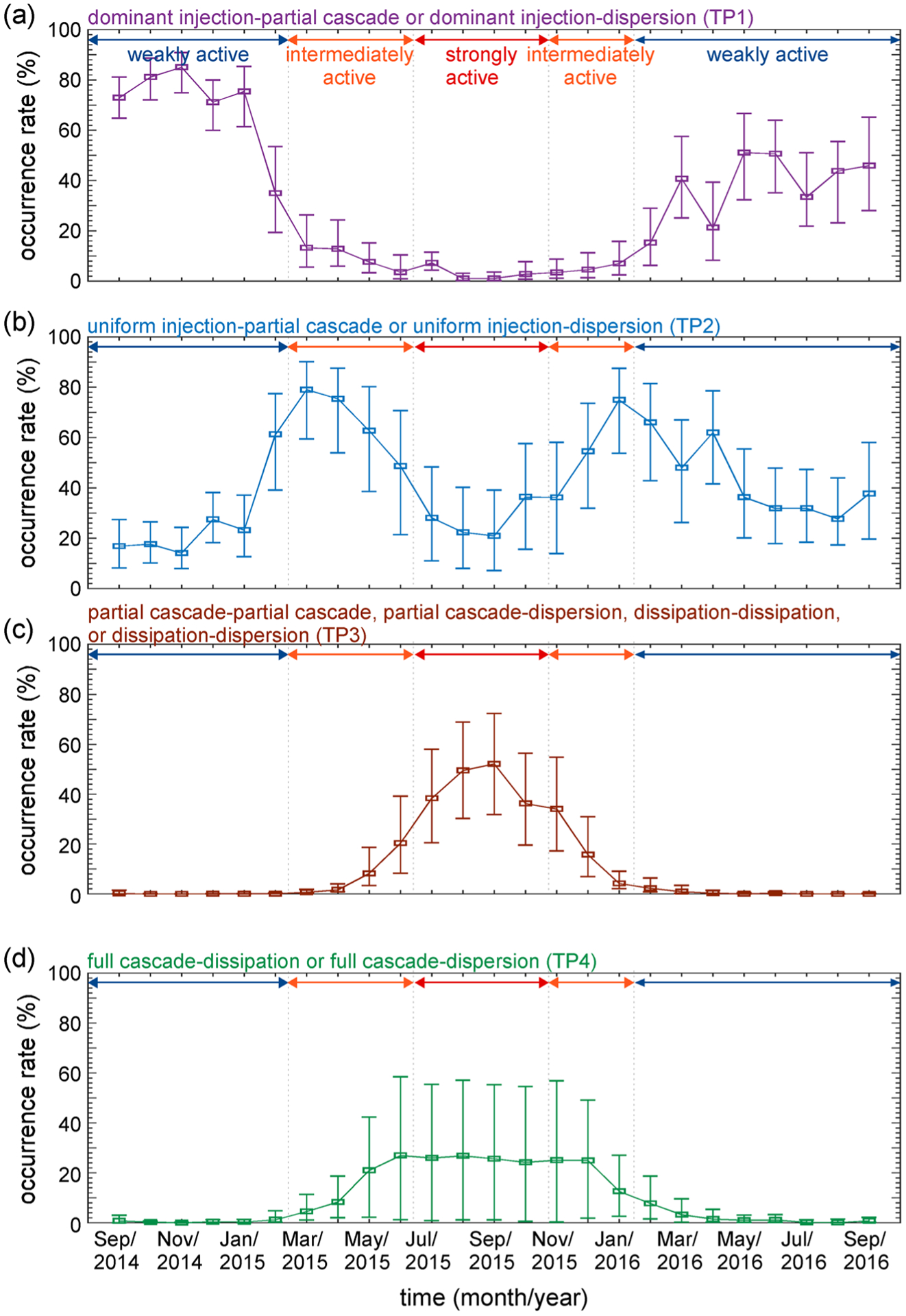
Occurrence rates for TP1–TP4 turbulent processes from September 2014 to September 2016 are shown in (a–d).

Figure 6.

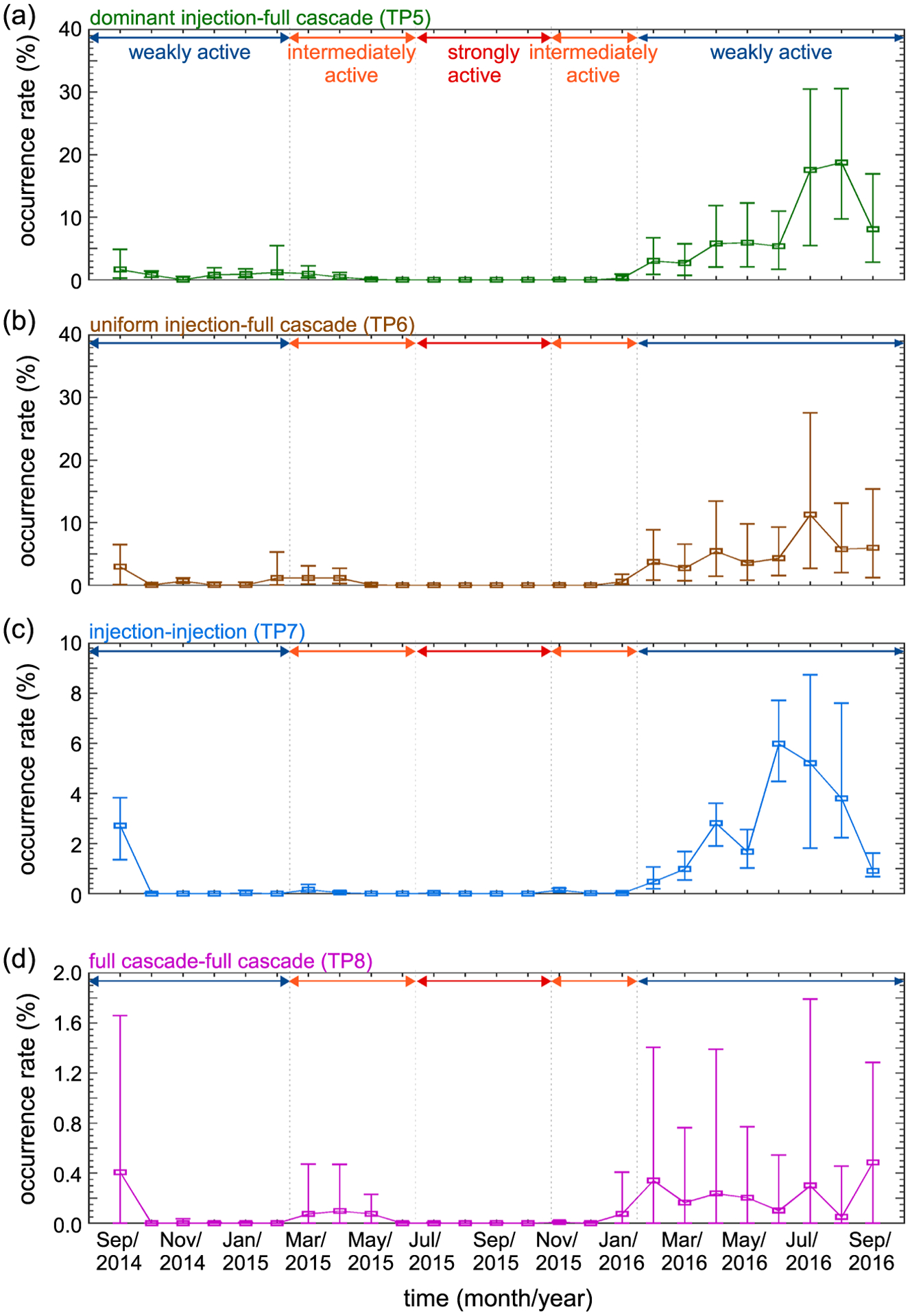
Occurrence rates for TP5–TP8 turbulent processes from September 2014 to September 2016 are shown in (a–d).

The turbulent process interpreted to be either uniform injection-partial cascade or uniform injection-dispersion (TP2) had the second-highest occurrence rate during the weakly active phase of the comet (see Figure 5b). During the transition from the weakly active phase to the intermediately active phase and also from the intermediately active phase to the weakly activity phase, the occurrence rate of TP2 peaked. During the intermediately active phase, the occurrence rate of TP2 was the highest among all the processes. However, during the strongly active phase, the occurrence rate of this process diminished and achieved an occurrence rate comparable to that during the weakly active phase. The turbulent process interpreted to be either partial cascade-partial cascade, partial cascade-dispersion, dissipation-dissipation, or dissipation-dispersion (TP3) was negligible during the weakly active phase of the comet. However, its occurrence rate increased during the intermediately and strongly active phases of the comet, becoming highest during the strongly active phase.

The occurrence rate of the turbulent process interpreted to be either full cascade-dissipation or full cascade-dispersion (TP4) was negligible during the weakly active phase of the comet. Its occurrence rate has large uncertainties for the intermediately and strongly active phases, which indicates that during that time, its occurrence rate could have been as low as 0% or as high as 60% (see Figure 5d).

The occurrence rate of the dominant injection-full cascade (TP5), uniform injection-full cascade (TP6), uniform or dominant injection-uniform or dominant injection (TP7), and full cascade-full cascade (TP8) generally remained relatively low for the period considered (see Figures 6a–6d).

5. Spatial Distributions of Turbulent Processes

To investigate the spatial distributions of the turbulent processes with the highest occurrence rates, specifically TP1, TP2, TP3, and TP4, we plot their spatial occurrence rates in Figure 7 for the weakly active phase and the intermediately and strongly active phases of the comet separately. The spatial maps shown in Figure 7 are plotted using the body-centered solar equatorial frame (CSEQ) in which the x axis points toward the Sun, the z axis is the component of the solar north pole perpendicular to the x axis, and y axis completes the right-handed coordinate system. We refer to X_CSEQ > 0 side of the comet or the sunward-facing side as the dayside and X_CSEQ < 0 side as the nightside of the comet.

Figure 7.

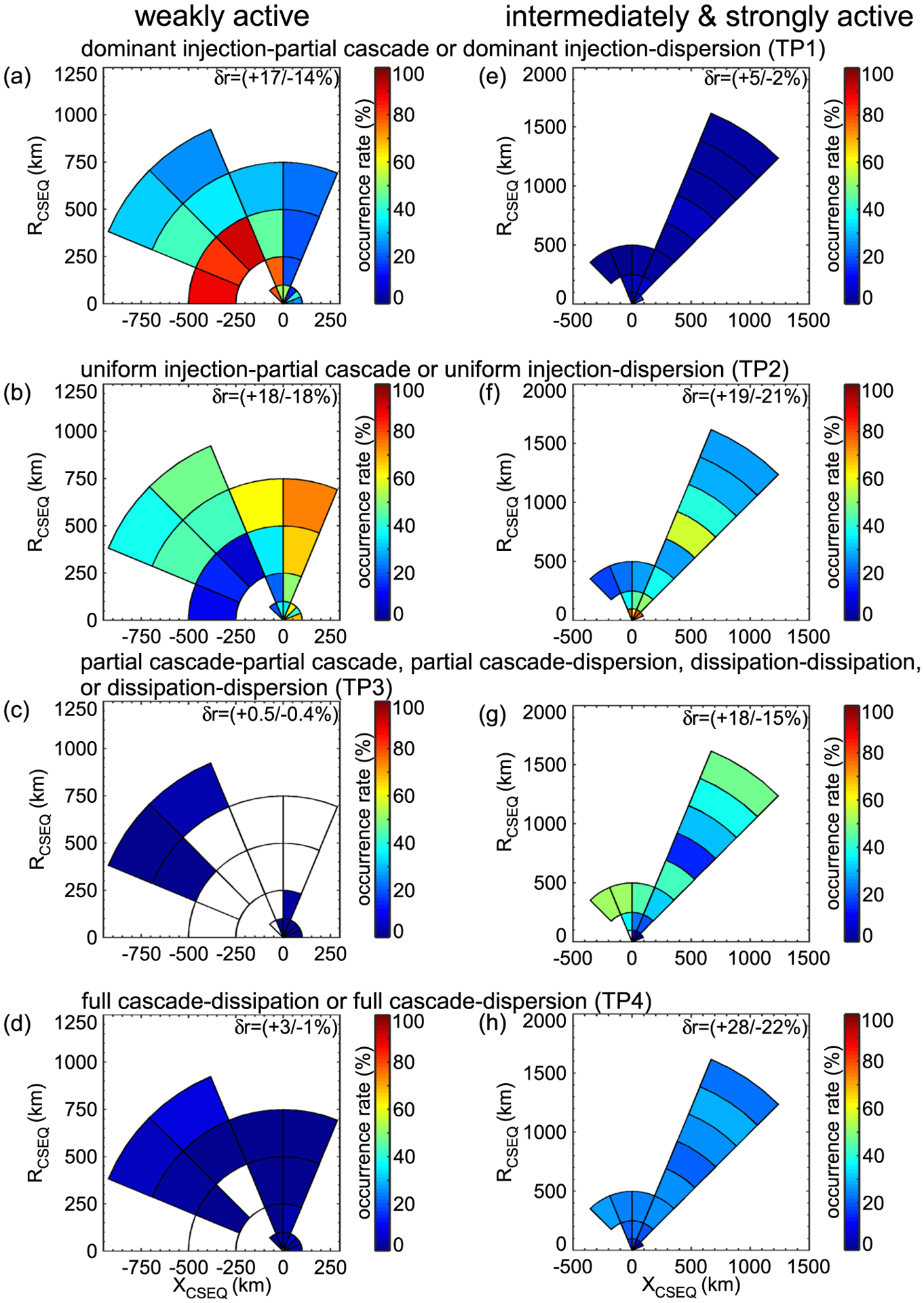
Spatial occurrence rate maps for TP1–TP4 turbulent processes during the weakly active phase are shown in (a–d). Spatial occurrence rate maps for TP1–TP4 turbulent processes during the intermediately and strongly active phases are shown in (e–h). In these figures, $R_{\mathit{\text{CSEQ}}}=\sqrt{Y_{\mathit{\text{CSEQ}}}^2+Z_{\mathit{\text{CSEQ}}}^2}$ is the radial distance from the comet. X_CSEQ > 0 side is the sunward side of the comet or the dayside. δr in each panel indicates the uncertainty of the occurrence rates.

During the weakly active phase of the comet, we find that TP1 had a high occurrence rate on the nightside than on the dayside (see Figure 7a), while TP2 process had a low occurrence rate on the nightside than on the dayside (see Figure 7b). TP2 had similar occurrence rates on both the dayside and nightside during comet’s intermediately and strongly active phases (see Figure 7f). The occurrence rates for TP2 were also much higher near the comet than farther from it during this time. The occurrence rates of TP3 were similar on both the dayside and nightside during the intermediately and strongly active phases of the comet (see Figure 7g).

6. Observability of Full Cascade at Comet 67P

Now, we turn to the observation of TP4, which had a large range for its occurrence rate from near 0% to 60% during the intermediately and strongly active phases of the comet. To make sense of this observation, in this section, we will attempt to answer the question, was observation of full cascade possible at comet 67P?

The spacecraft speed was <30 m/s which is much smaller than the bulk flow speed V_bulk of plasma at the comet and the Alfvén speed V_A (see Table 3 for typical values for these parameters at comet 67P). Thus, fluctuations observed by the spacecraft should have been the ones that convected past the spacecraft due to the bulk flow of the plasma past the spacecraft or the waves that reached the spacecraft that overcame the plasma flow away from the spacecraft. The latter case is certainly possible within the solar wind ion cavity and the diamagnetic cavity where the Alfvén speed can exceed the bulk plasma flow speed. Full cascade can be observed in a plasma environment if the nonlinear timescales T_NL associated with energy cascade are much smaller than the time it takes for the fluctuations to be observed after their generation T_obs. We can estimate T_obs as T_obs = T_CV or T_obs = T_A, where T_CV = R_s/V_bulk is the convection time and T_A = R_s/V_A is the Alfvén time. Here, R_s is the interaction scale size of the comet.

Table 3.

Evaluation of the Observability Criteria for Full Cascade at the Comet

Parameter	Weakly active comet	Intermediately/strongly active comet
Vbulk (km/s)	30–600	2–40
VA (km/s)	4–305	5–27
δb (nT)	1.3–3.2	3.5–7.9
δVA (km/s)	0.5–45	0.9–5.7
Rs (km)	1,000	400–800
τc (s)	135–1,557	117–837
TNL1 = τcVbulk/δVA (s)	90–1.8 × 106	41–3.7 × 104
TNL2 = τcVA/δVA (s)	12–9.5 × 105	102–2.5 × 104
Tobs1 = TCV = Rs/Vbulk (s)	2.7–33	10–400
Tobs2 = TA = Rs/VA (s)	3.3–250	15–160
Tnl1/TCV	2.7–1.1 × 106	0.1–3.7 × 103
Tnl2/TA	0.05–2.9 × 105	0.6–1.7 × 103

Note. V_A and V_bulk are computed by using the parameters listed in Table 1.

The nonlinear times can be estimated as T_NL = τ_cV_bulk/δV_A (Saur et al., 2002) or T_NL = τ_cV_A/δV_A, where τ_c is the autocorrelation time and δV_A = V_AδB. To estimate τ_c, first, we computed the autocorrelation for the magnetic field as < B(t + τ)B(t) >/< B(t)B(t) >, where τ denotes the time increment and <> denotes the mean. We repeated this for many time intervals for each month and computed the median and quartiles for magnetic field autocorrelation function (see a couple of examples shown in Figures 8a and 8b). The autocorrelation time is the time where the autocorrelation function attains a value of e⁻¹. We used the autocorrelation function curves associated with the median and the quartiles to estimate the median autocorrelation time and its uncertainties. We plot the autocorrelation times and their uncertainties for each month in Figure 8c. τ _c values often had a smaller range of values during the intermediately and strongly active phases than during the weakly active phase as can be seen in Figure 8c. We use the median autocorrelation times and quartiles computed in the weakly active and intermediately/strongly active phases separately to determine the range of values possible for τ _c for these times and list them in Table 3. We use these values along with the nominal values of V_bulk, V_A, and δV_A to estimate T_NL, which are also listed in Table 3.

Figure 8.

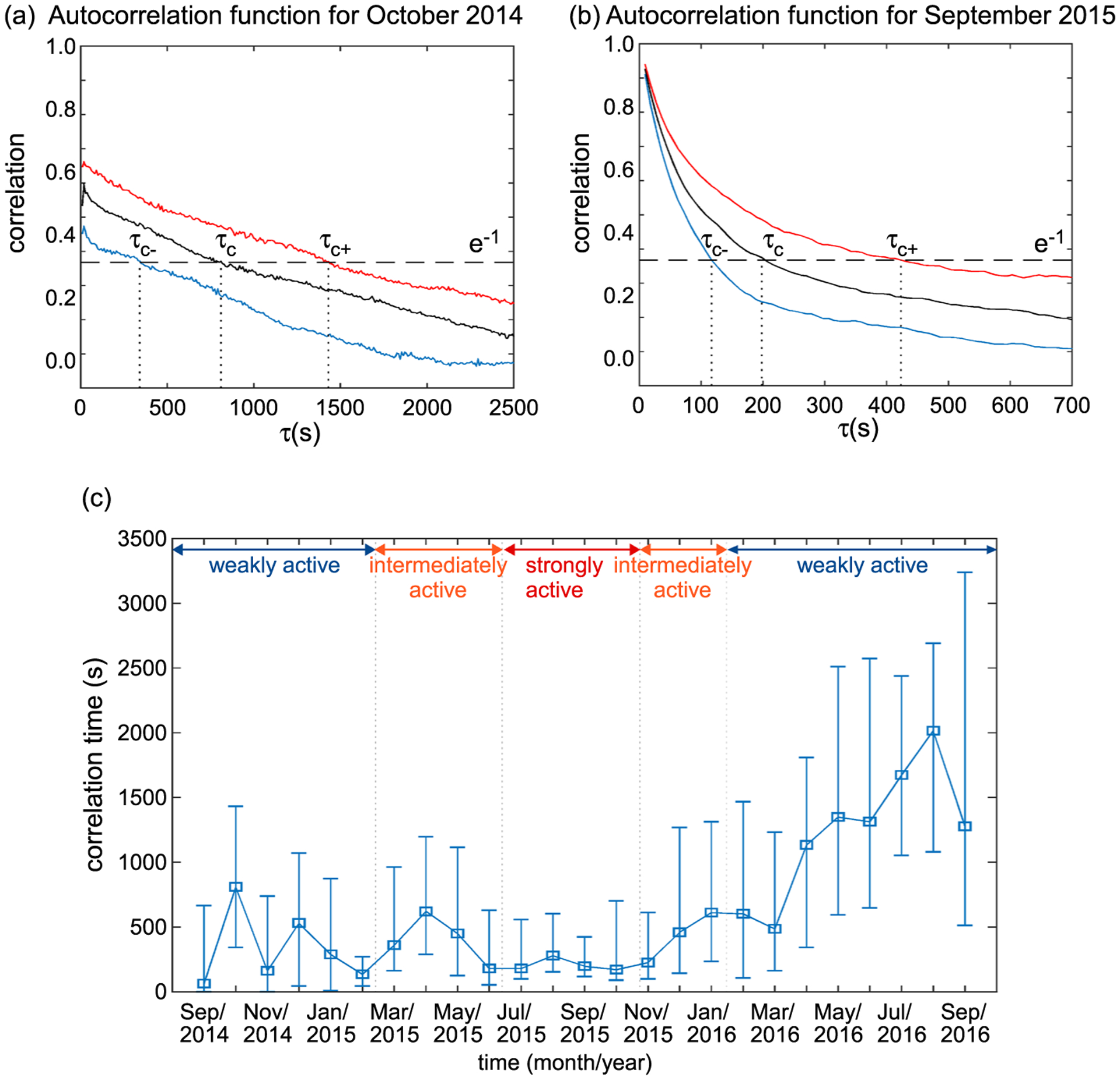
Median and quartiles of autocorrelation function for magnetic field for two representative times are shown in (a) and (b). Median correlation times and their uncertainties for each month from September 2014 to September 2016 are shown in (c).

We use R_s ≈ 1,000 km for the weakly active phase (Glassmeier, 2017) and use R_s ≈ 400–800 km for the intermediate/strongly active phases, which is the estimated size range for the solar wind ion cavity/diamagnetic cavity (Behar et al., 2017), to compute T_CV and T_A using values for V_bulk and V_A. In Table 3, we list the T_NL/T_CV and T_NL/T_A ratios estimated for the weakly active phase and the intermediately/strongly active phases separately.

We find that T_NL/T_CV and T_NL/T_A are biased toward values which are much greater than 1, which is not favorable for the observation of full cascade at comet 67P. However, the T_NL/T_CV and T_NL/T_A ratios have a much smaller range of values during the intermediately and strongly active phases than during the weakly active phase, which implies that full cascade can have a higher probability for observation during the intermediately and strongly active phases of the comet. Thus, TP4 may had a higher occurrence rate during that time than during the weakly active phase. However, T_NL/T_CV and T_NL/T_A ratios do not favor an occurrence rate for TP4 as large as 60%.

7. Discussion and Conclusions

Our main discovery is that different turbulent processes became prominent during the different active phases of the comet 67P. During the weakly active phase of the comet, TP1 was dominant, followed by TP2. During the intermediately active phase, TP2 was dominant, followed by TP3. During the strongly active phase, TP3 was dominant, followed by TP2.

The pristine solar wind should have full cascade in the low-frequency range and dissipation in the high-frequency range (full cascade-dissipation for short) (Kiyani et al., 2015) for the frequency range that we surveyed. We find near 0% occurrence rate for the TP4 process, as described in section 4, which is the turbulent process interpreted to be either full cascade-dissipation or full cascade-dispersion, during the weakly active phase. This observation indicates that the plasma turbulent characteristics at comet 67P were significantly different from those of the pristine solar wind during the weakly active phase.

The high occurrence rate of TP1 during the weakly active phase (see section 4) indicates that dominant injection occurred preferentially at low frequencies at comet 67P during that time. The dominant injection at low frequencies should be due to the ion Weibel instability, as the low-frequency waves inferred to be excited by this instability were also prominently observed during the weakly active phase of the comet (Glassmeier, 2017). The higher occurrence rate of TP1 on the nightside than on the dayside during the weakly active phase, as described in section 5, indicates that dominant injection was preferentially observed on the nightside than on the dayside. The reason for this asymmetry remains an open question. However, a possibility is the role that the wave growth rate might have played in the observability of the waves. If the growth rates are low, the waves require some convection/propagation time before they attain a sufficient amplitude in order to be detected. If this is indeed the case, the waves that are excited on the dayside, which have low amplitudes, can be discerned preferentially on the nightside as they have larger amplitudes on the nightside due to the wave growth.

The high occurrence rate of TP2 during the transition times between the weakly active phase and the intermediately active phase (see section 4) indicates that uniform injection was prominent for low frequencies during these times. This is also near the time Gunell et al. (2018) reported the observation of the formation of a bow shock near comet 67P. For planetary plasma environments, uniform injection is often observed at low frequencies downstream of a bow shock in shocked and thermalized solar wind (Ruhunusiri et al., 2017). Thus, we find that the turbulent processes at comet 67P, at least for the low frequencies, are similar to those that occur downstream of planetary bow shocks near the times when it was in the process of developing a bow shock. While the exact sources of the uniform injection remain unknown, possible sources of uniform injection at a cometary plasma environment, in general, can include instabilities that can be excited due to pickup ions and temperature anisotropies (Hada & Matsumoto, 1997).

TP1, which indicates the presence of dominant injection at low frequencies, was observed with a much lower occurrence rate during these transition times (see section 4). A possibility for the observation of the lack of dominant injection at these transition times could be masking of the dominant injection processes by uniform injection processes that occur during these times. Such masking of monochromatic waves has indeed been observed at other planetary plasma environments (Ruhunusiri et al., 2018).

During the intermediately and strongly active phases of the comet, Rosetta mainly orbited the comet within the solar wind ion cavity while also making frequent short-duration excursions to the diamagnetic cavity as described in section 1.2. As we find a high occurrence rate for TP2 and TP3 during the intermediately and strongly active phases, as described in section 4, the dominant processes that occurred in the low frequencies within these plasma environments are uniform injection and either partial cascade, dissipation, or both. Since the solar wind flow is absent within the solar wind ion cavity, the turbulent processes that we identify for the intermediately and strongly active phases should be mainly those that occurred within the solar wind ion cavity and the diamagnetic cavity rather than the turbulent processes that were generated at the bow shock or in the shocked and thermalized solar wind downstream of the bow shock.

Partial cascade and dispersion are the possibilities for the high-frequency turbulent processes that occurred at comet 67P during the weakly active phase of the comet since we observe TP1 and TP2 with a high occurrence rate during that time as described in section 4. Partial cascade, dissipation, and dispersion are the possibilities for the turbulent processes that occurred at the comet in the high-frequency range during the intermediately and strongly active phases of the comet since we observe high occurrence rates for TP2 and TP3 during those times.

We find that the T_NL/T_obs ratios generally have larger values as discussed in section 6, which indicates that the plasma environment of comet 67P did not provide sufficient time for the energy cascade to develop fully and be observed by the Rosetta spacecraft. This is consistent with our finding of the partial cascade as one of the possibilities for high-frequency processes. However, T_NL/T_obs ratios have a much lower range of values during the intermediately and strongly active phases of the comet than during the weakly active phase of the comet (see section 6), which implies that full cascade could have been observed with a higher probability during the intermediately and strongly active phases of the comet. Thus, TP4 could have had a higher occurrence rate during that time. The large uncertainties of TP4 indicate that its occurrence rate could have been as low as 0% or as high as 60% during the intermediately and strongly active phases. However, T_NL/T_obs ratios do not favor an occurrence rate for TP4 as large as 60%. If full cascade occurs generally in a cometary plasma environment, it should have important implications for the energy budget of the comet such as substantially heating the plasma in its environment.

Key Points:

• Plasma turbulent processes at comet 67P vary temporally as it orbits the Sun

• For low frequencies, energy injection and partial energy cascade or dissipation are dominant

• For high frequencies, partial energy cascade, dissipation, or dispersion is dominant

Data Availability Statement

The Rosetta magnetometer data (https://www.cosmos.esa.int/web/psa/rosetta) and data analysis software (https://doi.org/10.5281/zenodo.3964959) are publicly available and can be accessed online.