Flexible pivoting of dynamin pleckstrin homology domain catalyzes fission: insights into molecular degrees of freedom

Abstract

The neuronal dynamin1 functions in the release of synaptic vesicles by orchestrating the process of GTPase-dependent membrane fission. Dynamin1 associates with the plasma membrane–localized phosphatidylinositol-4,5-bisphosphate (PIP₂) through the centrally located pleckstrin homology domain (PHD). The PHD is dispensable as fission (in model membranes) can be managed, even when the PHD-PIP₂ interaction is replaced by a generic polyhistidine- or polylysine-lipid interaction. However, the absence of the PHD renders a dramatic dampening of the rate of fission. These observations suggest that the PHD-PIP₂–containing membrane interaction could have evolved to expedite fission to fulfill the requirement of rapid kinetics of synaptic vesicle recycling. Here, we use a suite of multiscale modeling approaches to explore PHD–membrane interactions. Our results reveal that 1) the binding of PHD to PIP₂-containing membranes modulates the lipids toward fission-favoring conformations and softens the membrane, and 2) PHD associates with membrane in multiple orientations using variable loops as pivots. We identify a new loop (VL4), which acts as an auxiliary pivot and modulates the orientation flexibility of PHD on the membrane—a mechanism that we believe may be important for high-fidelity dynamin collar assembly. Together, these insights provide a molecular-level understanding of the catalytic role of PHD in dynamin-mediated membrane fission.

INTRODUCTION

Dynamin is a multidomain GTPase that self-assembles into a helical collar and catalyzes membrane fission, leading to the release of nascent clathrin-coated vesicles during endocytosis (Koenig et al., 1983; Van der Bliek et al., 1993; Faelber et al., 2011; Morlot and Roux, 2013; Dar and Pucadyil, 2017). The GTPase domain (G-domain), bundle-signaling element (BSE), and stalk domain are the three conserved domains in dynamin that are required to evoke stimulated GTPase activity upon self-assembly on the membrane (Chappie and Dyda, 2013). In addition to these domains, classical dynamins contain a proline-rich domain (PRD) that interacts with SH3 domain–containing partner proteins and a pleckstrin-homology domain (PHD) that binds to plasma membrane–localized lipid phosphatidylinositol-4,5-bisphosphate (PIP₂). GTP hydrolysis is proposed to orchestrate a series of conformational changes in the self-assembly to surmount the activation barrier to membrane fission (Chernomordik and Kozlov, 2003; Schneck et al., 2012).

Structurally, the ubiquitous dynamin1 PHD has a C-terminal α-helix and a core β-sandwich with variable loops between the β-strands that form the binding pocket for PIP₂. The crystal structure of dynamin1 PHD (PDB: 1DYN) suggests a β-sandwich structure with two β-sheets, one with four and the other with three β-strands, oriented in an antiparallel arrangement. The structure defines four loops referred to as variable loops (VLs) as shown in Figure 1. These loops significantly differ from each other in hydrophobicity and electrostatics. VL1 (⁵³¹IGIMKGG⁵³⁷) contains a hydrophobic stretch that inserts in the membrane and assists dynamin’s subcellular localization (Ramachandran and Schmid, 2008). VL3 (⁵⁹⁰NTEQRNVYKDY⁶⁰⁰) is highly polar and has also been shown to be important for membrane association (Liu et al., 2011; Francy et al., 2015). While the PHD helps classical dynamins to engage with the membrane (Okamoto et al., 1997; Ferguson and De Camilli, 2012), numerous lines of evidence suggest that it functions more than a generic membrane anchor (Klein et al., 1998; Achiriloaie et al., 1999; Vallis et al., 1999; Ramachandran et al., 2009; Mehrotra et al., 2014; Reubold et al., 2015; Terzi and Deserno, 2016; Dar and Pucadyil, 2017). Genetic neurological disorders such as centronuclear myopathies and Charcot–Marie–Tooth disease are linked to mutations in the PHD that map to regions distinct from those involved in membrane binding (Durieux et al., 2010; Kenniston and Lemmon, 2010; Haberlová et al., 2011). Cellular assays combined with biochemical and microscopic analysis of membrane fission with point mutants in the PHD of dynamin1 suggest that this domain might induce local membrane curvature by shallow insertion of one of its loops (Ramachandran et al., 2009) and that such point mutations alter the dynamics and orientation of the PHD on the membrane (Mehrotra et al., 2014). Experimentally guided modeling has shown that tilting of the PHD could be responsible for creating a low-energy pathway toward reaching the hemi-fission state (Shnyrova et al., 2013). GTP hydrolysis is required to initiate fission through constriction (Antonny et al., 2016), but whether this is adequate to achieve complete and leakage-free vesicle scission is still under debate (Shnyrova et al., 2013; Mattila et al., 2015). Recent models indicate that the GTPase-driven scaffold constriction brings the membrane in close proximity but not close enough to cross the energy barrier for fission and that stochastic fluctuations are responsible for the cross-over from the constricted stage to the hemi-fission state (Terzi and Deserno, 2016; McDargh and Deserno, 2018). Indeed, analysis of membrane fission at the single-event resolution indicates that replacement of the PHD-PIP₂ interaction with a generic lipid–protein interaction forms long-lived, highly constricted prefission intermediates on the membrane that results in dramatic dampening of fission kinetics (Dar and Pucadyil, 2017). Recent cryo electron microscopy (cryo-EM) data of the dynamin polymer assembled on tubular membranes reveal complex and variable geometries of the PHD (Shnyrova et al., 2013; Sundborger et al., 2014; Mattila et al., 2015; Kong et al., 2018). The variable PHD configurations may reflect an evolutionary requirement for generating membrane torque necessary for traversing a pathway whereby membrane constriction guarantees leakage-free fission as shown in some of the recent models (Pannuzzo et al., 2018).

FIGURE 1:

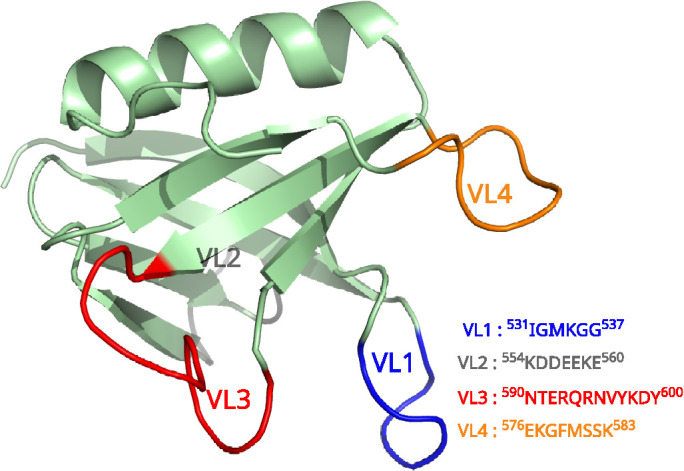
PHD and its variable loops.

Guided by these observations, and to circumvent the difficulty of observing short-lived transition states of PHD-PIP₂ interaction in an experimental scenario, we apply multiscale molecular simulations to study the membrane association behavior of dyn-PHD in great molecular detail. Undulation spectra extracted from Martini coarse-grained (CG) trajectories of large membrane systems (with and without PHD) were used to observe the effect on membrane physical properties. These methods also test the hypothesis of local curvature generation by the PHD. We then explore the conformational changes induced by PHD in lipids of the membrane using all-atom molecular dynamics (AAMD) simulations. Mixed-resolution highly mobile membrane-mimetic model (HMMM)-based MD simulations initiated from different orientations were used to explore possible membrane association pathways. Membrane association geometries were deciphered using data from both AAMD simulations and by free energy difference calculations from enhanced sampling methods such as metadynamics and umbrella sampling simulations. PHD is a ubiquitous membrane adaptor, and PHD–membrane interactions have been studied thoroughly for several proteins in great detail both in experiments and using molecular simulations (Ferguson et al., 1995; Klein et al., 1998; Lemmon and Ferguson, 2000; Lai et al., 2013; Srivastava and Voth, 2014; Jian et al., 2015; Vonkova et al., 2015; Yamamoto et al., 2016, 2020; Naughton et al., 2016, 2018; Chan et al., 2017; Pant and Tajkhorshid, 2020; Soubias et al., 2020). In our work, we also look at the membrane association mechanism and intricate binding geometries and interactions of dyn-PHD in light of other available studies and highlight the similarities and differences while connecting the PHD–membrane interactions to dynamin-assisted fission process (Achiriloaie et al., 1999; Lee et al., 1999; Ramachandran et al., 2009; Shnyrova et al., 2013; Mehrotra et al., 2014; Dar et al., 2015; Dar and Pucadyil, 2017). Together, our results indicate that the presence of the PHD causes significant changes in lipid conformations and the membrane-bending rigidity, thus providing mechanistic insights into its catalytic effect on membrane fission due to dynamin. These effects are managed by flexible pivoting of the previously described variable loop1 (VL1) and the yet-unexplored variable loop (VL4) in the PHD with the membrane.

RESULTS AND DISCUSSION

Significance

Dynamin, a large multidomain GTPase, remodels the membrane by self-assembling onto the neck of a budding vesicle and induces fission by its energy-driven conformational changes. In this work, we use multiscale molecular simulations to probe the role of dynamin’s PHD, which facilitates membrane interactions. Notably, PHD is dispensable for fission, as is the case with extant bacterial and mitochondrial dynamins. However, reconstitution experiments suggest that the functional role of PHD in neuronal membrane goes beyond that of an adaptor domain as it possibly “expedites” the fission reaction during synaptic vesicle recycling. We provide a MD picture of how PHDs make membranes more pliable for fission and suggest new insights into the molecular-level processes driving the expedited fission behavior.

Binding of the PHD renders the membrane pliable for fission

To determine the effect of the PHD on the mechanical properties of the membrane, we performed 4-μs-long CG simulations of a large lipid bilayer patch (∼625 nm²) using the Martini force field (Marrink et al., 2004). This bilayer is composed of 2048 lipids with DOPC:DOPS:PIP₂ in a 80:19:1 molar ratio. Fourteen CG PHD units were placed randomly onto one of the leaflets of the bilayer. The bending moduli calculated by fitting undulation spectra to regular Helfrich theory (see Figure 2) show that the presence of the PHDs reduces the bending modulus (BM) of the lipid bilayer. We notice that the BM (K_c) of the membrane with PHDs is ∼4.5 k_BT lower than that without PHDs. To gain insights into the molecular structures and changes related to the two-dimensional density structure factor of the membrane, we plotted the full height undulation spectra (see Supplemental Figure S1) with larger q-regimes (Brandt et al., 2011). We observed some differences between the two spectra in the intermediate q regime but observed no noticeable difference in in-plane molecular structure fluctuations in the larger q regime while interpreting and comparing the full spectra. Analyses of trajectories did not reveal any noticeable protrusion modes, which we had anticipated from the differences that we saw in the intermediate q-regimes.

FIGURE 2:

Height-height undulation spectra for the two Martini CG systems. Spectra (A) with 2048 lipids and (B) with membrane and 14 CG PHDs distributed randomly on the bilayer surface. The schematics of the system, rendered from a snapshot of the trajectory, are shown in the inset. The undulation spectra follow the standard Helfrich-type q⁴ scaling, and the effect of curvature on the BM is not significant. Full fluctuation spectra for CG systems comprising 2048 lipids with pure membrane (no PHD) and membrane with 14 PHD are shown in Supplemental Figure S1. Time-averaged mean curvature observed in (C) pure membrane and (D) membrane with PHDs. Time-averaged Gaussian curvature observed in (E) pure membrane and (F) membrane with PHDs.

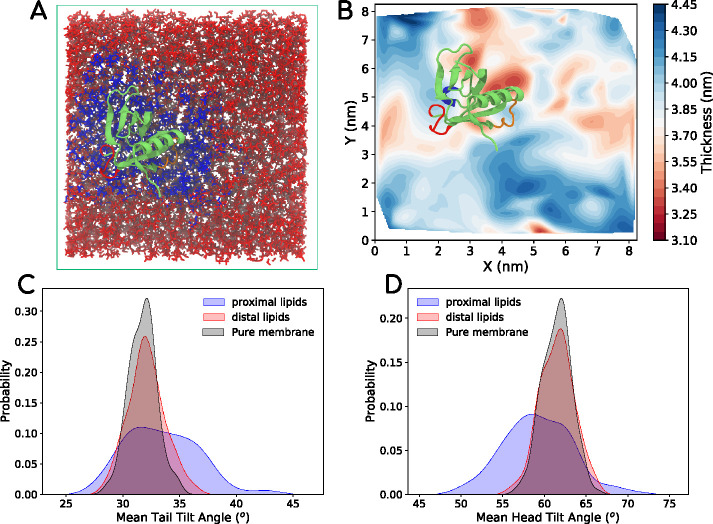
On the basis of our finding that the presence of the PHD lowers the BM of the membrane, we wanted to explore the molecular origin of decrease in BM. For this, we generated a microsecond-long atomistic trajectory of a single PHD on a lipid bilayer composed of DOPC:DOPS:PIP₂ (80:19:1) and observed the membrane thickness and lipid conformations (tilt and splay) of lipids proximal and distal to the PHD on the membrane. Figure 3A shows a snapshot of the bilayer-PHD system with the proximal and distal lipids marked in different colors. We define lipid splay as the distance between the terminal carbon atoms on each tail of the lipid. Lipid tail tilt is defined by the angle between the membrane normal and the vector formed by the glycerol carbon and the last tail atom on the chains. We report the average of the two values per lipid for tail tilt. Lipid head tilt is defined by the angle between the P-N vector (vector formed by phosphorus and nitrogen atom in the lipid) and the membrane normal. Figure 3B shows the variation of membrane thickness across the cross-section of the bilayer observed at the end of 500 ns (converged state). Remarkably, the PHD influences the underlying membrane by thinning it by as much as 0.4 nm (Figure 3B), which would have a bearing on the BM (Deserno, 2007). Similar analyses for different 250-ns-long time-averaged plots show that membrane thinning is tightly coupled to the location of the PHD (Supplemental Figure S2, top panel). The change in thickness comes due to changed molecular configurations of lipids proximal to the PHD. Indeed, the presence of the PHD leads to a positive lipid splay in proximal lipids (Agrawal et al., 2016) and is seen by measurements of the lipid tail (Figure 3C) and head (Figure 3D) tilt angles for a 25 ns time period. As seen in Figure 3, C and D, the presence of the PHD induces significant fluctuations in the tail and head tilt angles in lipids proximal to the PHD than in the distal lipids or in lipids in a membrane without the PHD. Snapshots of tilt and splay for a proximal and distal lipid are shown in Supplemental Figure S2 and highlight the extent to which the PHD influences local lipid dynamics. The ability of PHD to induce such noticeable changes in tilt fluctuations of lipids strongly suggests the possibility that its engagement with the membrane could prime proximal lipids to attain nonbilayer intermediates and thereby lower the energy barrier for fission (Shnyrova et al., 2013; Mattila et al., 2015; McDargh and Deserno, 2018; Agrawal and Ramachandran, 2019). Importantly, the changes seen in the tilt values and the higher populations of tilt angles deviating from the average emphasize the need to go beyond the simple Helfrich-like elastic sheet models of membranes, including augmented models such as the ones with undulation-curvature coupling (Bradley and Radhakrishnan, 2016), to understand the energetics of membrane remodeling in terms of finer molecular degrees of freedom such as lipid tilt and splay (Nagle, 2017; McDargh and Deserno, 2018).

FIGURE 3:

(A) Snapshot from an all-atom DOPC-DOPS-PIP₂ bilayer system with a single PHD (shown in light green) on the leaflet at the top. The lipids proximal to the protein are marked in blue. The distal lipids are marked in red. The lipids were tracked for 500 ns for the analysis. (B) Thickness profile of the bilayer with the PHD, showing thinner regions in red and thicker regions in blue. (C) Average tail angle distribution of lipids proximal to the protein (blue), distal to the protein (red), and in pure bilayer with no proteins (black). (D) Average head angle distribution of lipids. In Supplemental Figure S2, we provide some more data with thickness profiles of replicates and visuals of lipid conformations near and far away from the PHD.

Together these results confirm that PHDs soften the bilayer and possibly create favorable lipid configurations that induce or stabilize the nonbilayer intermediate topologies in the course of membrane fission. The implications of these molecular degrees of freedom in terms of the two paradigmatic models of membrane fission, namely the “constriction/ratchet model” (Leibler, 1986; Shlomovitz et al., 2011; McDargh and Deserno, 2018) and the “catalytic model” (Shnyrova et al., 2013; McDargh and Deserno, 2018) are discussed in detail later in the text.

In addition to bending modulus calculation, we performed local curvature calculations on CG lipid bilayer patch systems to observe spatial correlation between position of induction of curvatures and position of PH domains. The local curvatures observed in these membrane systems are quite dynamic in nature (see supporting data : mean-curvature.mp4 and gaussian-curvature.mp4). To observe curvatures that are persistent over time (and not simply thermal fluctuations), we performed time-averaging of mean (Figure 2, C and D) and Gaussian curvatures (Figure 2, E and F) observed at each point of the membrane surface. As seen in Figure 2D the lipid bilayer patch with PHDs does exhibit small scattered patches of both positive (green) and negative (purple) Gaussian curvatures (though small in magnitude) while pure membrane exhibits predominantly zero curvature (white color). In particular, there is one particular region on the membrane where a noticeable purple patch is seen and this corresponds to the region where a few PH domains are closely positioned. To some extent, this observation suggests that PH domains may be inducing a negative Gaussian curvature (saddle regions) on the membrane. To further test for curvature induction, we also created a hypothetical system where the PH domains were arranged in double collar – this was done to crudely model the scaffold and with an intention to accentuate the effect of PH Domain on curvature induction (see Figures R1-R4 in the supporting information).

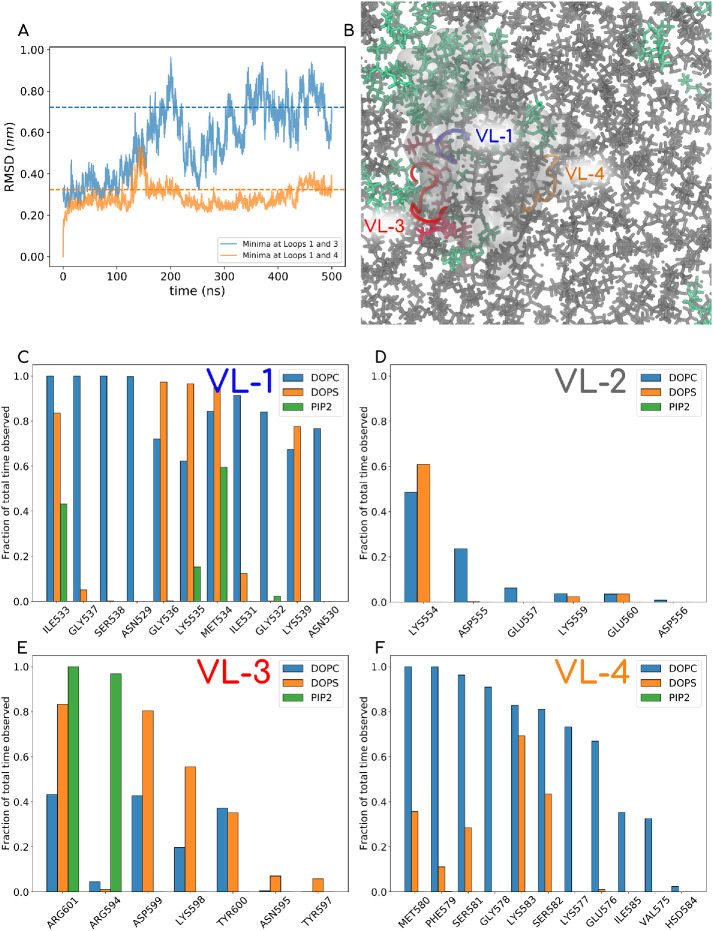
Dynamin PHD engages the VL4 loop as an auxiliary pivot that regulates its orientation flexibility

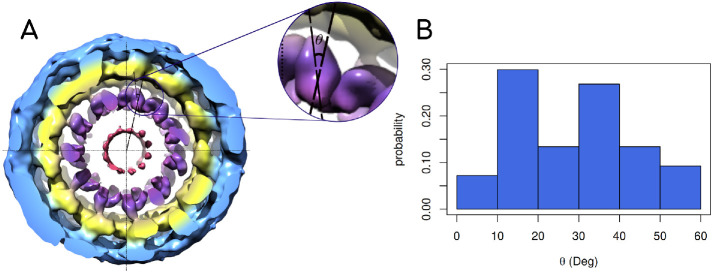
Recent cryo-EM reconstructions of the dynamin polymer assembled on a membrane report a super-constricted state at 10.1 Å resolution, which highlights localized conformational changes at the BSE and GTPase domains that drive membrane constriction on GTP hydrolysis (Sundborger et al., 2014; Kong et al., 2018; Dandey et al., 2020). We reconstructed these data and focused on the PHD orientation by taking slices across the collar, which provided us some interesting observations (Figure 4A). PHD orientation about a ring of the dynamin polymer was measured by plotting the distribution of the angle between the major inertial axis of each PHD and the vector that connects the center of the ring with the centroid of the PHD (Figure 4B; see inset in Figure 4A for a schematic of the angle measurement for a single slice). This analysis revealed that the membrane-bound PHDs adopt a wide range of orientations in the polymer. This is also apparent in other slices analyzed in the polymer (Supplemental Figure S3). The wide range of PHD orientations, even in the highly packed constricted state of the dynamin polymer, suggests that the PHD has an inherent ability to associate with the membrane in multiple orientations.

FIGURE 4:

(A) End view of the 3D density map of dynamin polymer assembled on the membrane. The radial densities colored in purple show the PHDs on the collar. The inset shows the angle that the end-to-end vector of a given PHD makes with the radial line passing through the centers of the tube and the given PHD. The density map is redrawn from the available cryo-EM density data by Jennifer Hinshaw (National Institute of Diabetes and Digestive and Kidney Diseases, NIH) and coworkers. (B) Probability distribution of angle described above in the cryo-EM map. The angle θ has a wide range for the constricted collar. In Supplemental Figure S3, we show reconstruction for six other slices.

To test this and to obtain molecular insights into the association between the PHD and the lipid bilayer, we carried out advanced mixed-resolution molecular simulations using the HMMM (Ohkubo et al., 2012; Vermaas and Tajkhorshid, 2014a; Baylon et al., 2016). This model utilizes a biphasic setup comprising lipids with short-chain fatty acyl chains (typically 3–5 carbon atoms long) organized around an organic solvent, 1,1-dichloro-ethane (DCLE), which mimics the hydrophobic core of the membrane. Many studies have shown remarkable success in probing membrane-protein interactions using HMMM model in MD simulations without compromising on the atomic details of the protein–lipid headgroup interface, because lipid diffusion in the bilayer is accelerated by an order of magnitude due to the absence of tail friction (Baylon et al., 2013; Blanchard et al., 2014; Vermaas and Tajkhorshid, 2014b; Pant and Tajkhorshid, 2020).We ran 12 different HMMM simulations with different initial orientations of the PHD on a bilayer composed of DOPC:DOPS:PIP₂ (80:19:1 mol%) and a DCLE hydrophobic core. Each system was run for at least 500 ns, with a total simulation time of ∼9.7 μs.

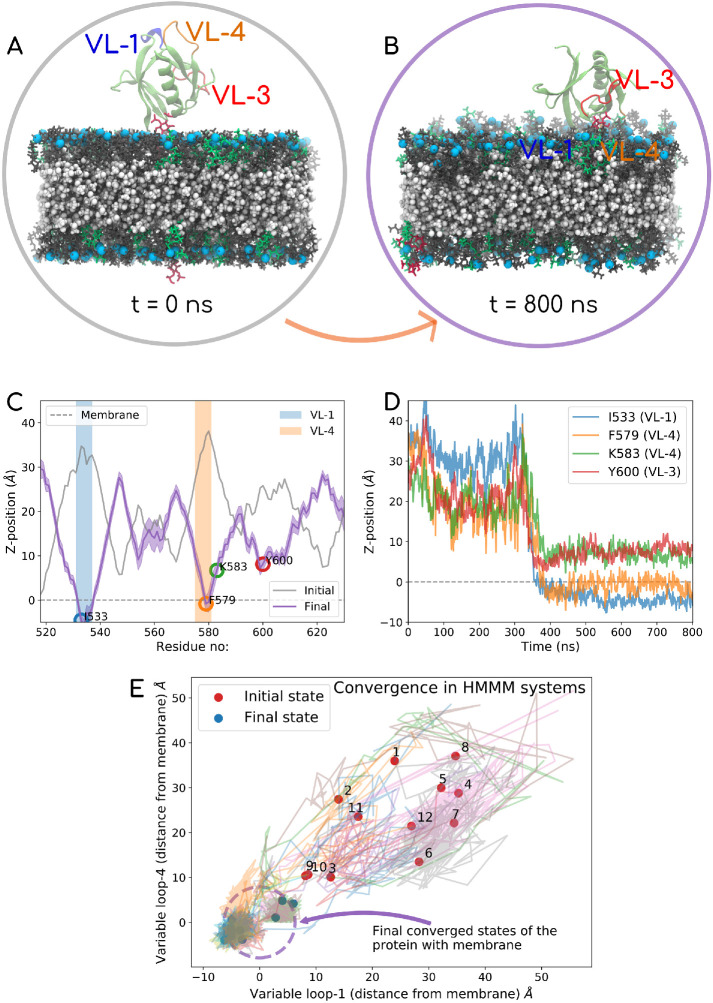
An important observation stands out from these simulations. In all our simulations, we consistently see that PHD associates with the membrane using both VL1 (⁵³¹IGIMKGG⁵³⁷) and VL4 (⁵⁷⁶EKGFMSSK⁵⁸³). VL3 (⁵⁹⁰NTEQRNVYKDY⁶⁰⁰) does not show direct membrane anchoring but is always proximal to the PIP₂ lipid headgroup that tends to “stick out” of the membrane plane. We explore this feature of VL3 more and put it in the context of existing literature (Liu et al., 2011; Mehrotra et al., 2014) when we discuss the binding geometries using the all-atom trajectories. In Figure 5 we have picked the extreme example from our HMMM runs where the initial PHD configuration is set up such that all the loops face away from the membrane (Figure 5A). The final configuration is shown in Figure 5B, where the VL1 and VL4 clearly partition into the membrane. Figure 5D shows the time evolution of residues on the various loops, and Figure 5C shows the initial and final z-distances for each residue with respect to the membrane phosphate plane. We have made a movie file for the full trajectory of this system, which is shared in Supplemental Movie-HMMM. The VL1, VL3, and VL4 loops are colored blue, red, and orange, respectively. The VL4 loop shows highly stable membrane association, and this observation is consistent across different starting configurations. In Figure 5E, we show the convergence data for each of the 12 systems by plotting the distances of the two loops from the membrane surface. Supplemental Figure S4 reports the initial and final membrane association profiles, in terms of z-distance of each residue away from the membrane plane for all 12 systems. The initial and the final orientations with respect to the membrane are also shown in insets of Supplemental Figure S4 for each of the 12 systems.

FIGURE 5:

Top panel shows the data for one of the 12 HMMM runs. In this case, the PHD is initially positioned such that all loops face away from the membrane. The PC, PS, and PIP₂ mimetic lipids are shown in gray, green, and red, respectively, and phosphorus is marked in light blue. DCLE is shown in white in the core of the bilayer. The VL1 of the PHD is shown in blue, VL3 in red, and VL4in orange color. The top panel shows the initial (A) and final (B) PHD configurations. (C) Initial and final z-distance of each of the residues averaged over the last 100 ns. (D) Time evolution of signature residues on different loops. The entire 800 ns trajectory data for this system are also reported in Supplemental Movie-HMMM). In the left panel, (E) shows the convergence data for all 12 HMMM systems, where the distance from the membrane surface for the VL1 loop (I533) on the x-axis and VL4 (F579) on the y-axis is tracked with time. Almost all systems converge to a configuration with VL1 and VL4 physically engaging with the membrane. Plot akin to one on the right panel is shown for all 12 systems in Supplemental Figure S4 (i–xii)

Movie S1.

Download video file ^{(80.3MB, mp4)}

All atom simulation data

Movie S2.

Download video file ^{(57.6MB, mp4)}

Mixed resolution movie file

Movie S3.

Download video file ^{(46.8MB, mp4)}

Gaussian Curvature movie file

Movie S4.

Download video file ^{(58.2MB, mp4)}

Mean Curvature movie file

Results on VL1 are consistent with previous studies indicating that it acts as a membrane anchor, and the I533A mutation on VL1 is known to destabilize this interaction and reduce the stability of the scaffold on the membrane in the wake of GTP hydrolysis (Klein et al., 1998; Achiriloaie et al., 1999; Lemmon and Ferguson, 2000; Bethoney et al., 2009; Ramachandran et al., 2009; Dar et al., 2015; Dar and Pucadyil, 2017). To gain further insights into how the I533A mutant affects the membrane association, we carried out AAMD simulations for wild-type (WT)-PHD and I533A-PHD on a bilayer composed of DOPC:DOPS:PIP₂ (80:19:1 mol%). Each system was run for at least 500 ns. Figure 6A shows the residue-wise z-distance for initial and final configurations for the WT system. Figure 6B shows the same data for the I533A system. To our surprise, the membrane association profile for the I533A did not show noticeable changes and the mutant does not seem to be membrane defective. We carried out similar AAMD runs on mutations on VL4 residues such as F579A and K583A (Figure 6, C and D), which also showed association behavior similar to that of WT. We anticipated these to be facile associations and carried out umbrella sampling calculations on the WT and various mutant systems to extract the binding free energy (ΔG) information. Figure 6E shows the membrane dissociation “potential of mean force” (PMF) profile for the WT and various mutant systems. As anticipated and reassuringly, there is a significant difference in membrane-binding free energies for the WT and I533A mutant system. This suggests that while the mutant I533A is nondefective with respect to membrane association, it binds superficially to the membrane and this explains the compromised assembly and reduced stability of the dynamin on the membrane.

FIGURE 6:

(A–D) Data for four of the AAMD simulation runs with respect to z-distance of each residue on the protein away from the membrane phosphate plane. The simulations were run for 500 ns each. The four systems are (A) WT, (B) I533A, (C) F579A, and (D) K583A. The gray curve on each figure indicates the initial configuration, and the blue curve is the final configuration averaged over the last 100 ns. Similar plots for K339A and Y600L mutant systems are shown in Supplemental Figure S7. (E) PMF profiles of the five systems obtained through umbrella sampling simulations. Right-most end of the graph denoted PHD in solution. The zero of the free energy difference plot is set at the phosphate plane of the membrane.

The analyses on F579A and K583A mutations shed some light on the role of VL4 as an auxiliary/secondary pivot. We chose to test the F579A mutation first because our HMMM simulations as well as our AAMD simulations consistently show that F579 has the deepest penetration for VL4. Interestingly, F579A hardly shows any change in binding free energies from the calculations done using umbrella sampling. K583A shows a minimal change of ∼2 kcal/mol in the dissociation ΔG values as compared with WT. It is clear that mutation on VL4 does not significantly alter the dissociation ΔG, so we checked whether these mutations had any effect on angular stability of the membrane-bound PHDs. To quantify the orientation flexibility of membrane-bound PHD, we looked at the angle that the PHD helix makes with the membrane normal θ (see inset of Figure 7A) and also the angle that it makes when projected to a reference axis on the membrane surface (φ), represented in the 360degree polar coordinate system. We compare the angles for WT data against I533A, F579A, and K583A (θ in Figure 7A and φ in Figure 7B). The distribution in WT is consistent with our cryo-EM reconstructions analysis (Sundborger et al., 2014; Kong et al., 2018) and further shows that the membrane-bound PHD is flexible in its orientation. However, VL4 mutations such as F579A and K583A show a significant increase in the range of angle distribution, while I533A shows hardly any change in the distributions. In our AAMD simulations and free energy calculations, we find that mutants have weaker membrane-binding free energy and many of them increase the orientation fluctuations of the PHD. We hypothesize that the mutation that makes the PHD highly labile (orientationally) adversely affects the collar assembly process, leading to compromised fission behavior. So even if, on the face value, the PHD is not membrane defective with VL4 mutants, the high orientation fluctuations are likely to affect the fission kinetics to a large extent. By attaching to the membrane using VL1 as the primary pivot and VL4 loop as the auxiliary pivot, the PHD stabilizes the dynamin on the membrane—in terms of both anchoring and orientation flexibility—thereby likely facilitating better assembly and collar formation. Incidentally, an artificially higher PIP₂ concentration on the membrane has a similar effect on rescuing the kinetics for the I533A mutation to some extent (Dar et al., 2015), which lends further credence to our theory. While a high PIP₂ concentration rescues the fission kinetics by increasing the “anchoring” binding energy, it will be interesting to check whether fission kinetics can be rescued for mutations that make the PHD unusually labile on the membrane. We carried out some tests toward that with double mutations as shown in Supplemental Figure S5.

FIGURE 7:

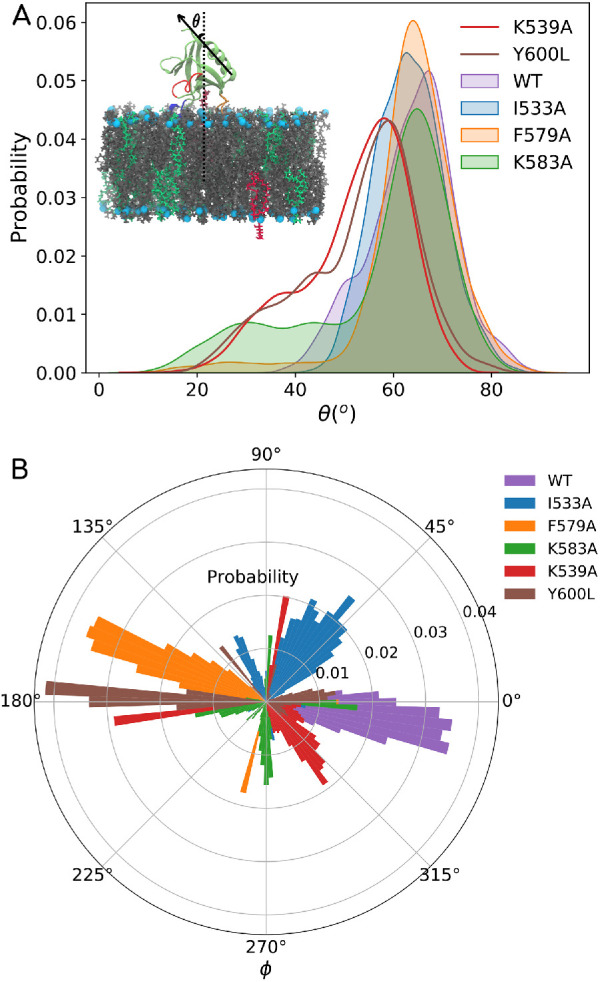
Data showing orientation distribution for PHD for WT and various mutant systems. (A) Inset in the top panel shows a schematic where θ is the angle that the helical axis makes with the membrane normal. θ angle distributions for the WT, I533A, F579A, K583A, Y600L, and K539A systems are shown in the top panel. (B) φ is the angle that the helical axis makes with a reference axis on the plane of the membrane and is shown in the bottom panel for all the WT and mutant systems.

Key residues stabilizing the PIP ₂-PHD binding are found in multiple VLs

The role of VL1 in dynamin-catalyzed vesicle scission is undisputed (Ramachandran et al., 2009; Shnyrova et al., 2013; Mehrotra et al., 2014; Dar et al., 2015; Dar and Pucadyil, 2017). Fission is shown to be impaired with VL1 mutants such as I533A and M534C that attenuate its hydrophobic character (Ramachandran and Schmid, 2008; Ramachandran et al., 2009). Several studies have also shown the importance of VL3 in stabilizing the membrane interaction of PHD (Lee et al., 1999; Vallis et al., 1999; Chappie et al., 2011; Liu et al., 2011; Mehrotra et al., 2014). Owing to its polar nature, VL3’s direct engagement with the hydrophobic core is thought to be unlikely and loss in function with mutations such as Y600L is primarily attributed to the overall instability of the dynamin polymer on the membrane surface (Mehrotra et al., 2014). Additionally, our work consistently shows that VL4 engages with the acyl-chain hydrocarbon core and likely acts as a secondary pivot or a “buoy” that stabilizes the protein on the surface. Cryo-EM maps of the dynamin polymer, reconstructed with different modeled orientations of the PHD, further reinforce the possibility of PHD associating with multiple orientation with the membrane (Chappie et al., 2011; Sundborger et al., 2014; Kong et al., 2018).

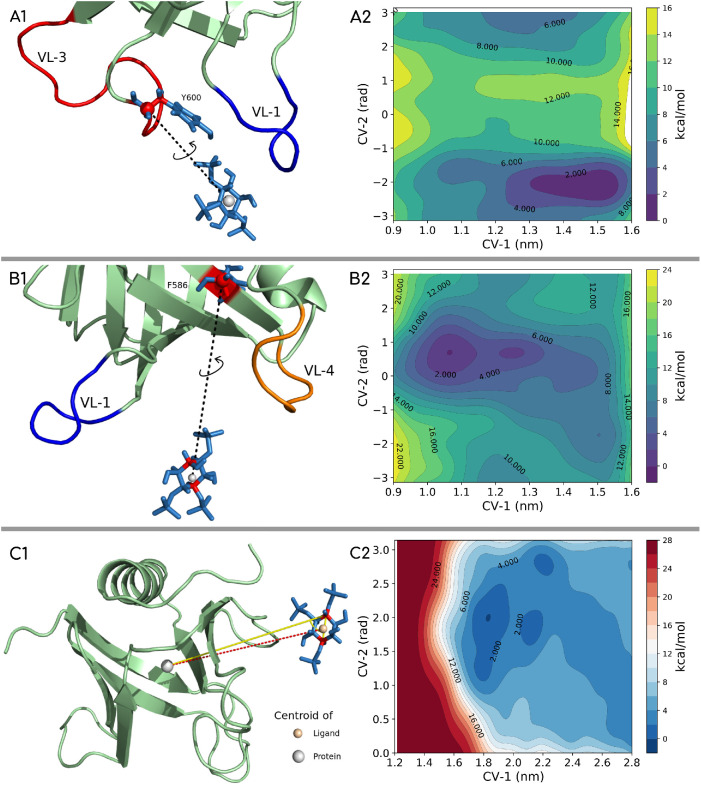
To test the multiple orientation and binding geometries and also to look more carefully into the molecular-scale features that possibly drive and stabilize these associations, we carried out well-tempered metadynamics (WT-MTD)-based enhanced-sampling simulations (Barducci et al., 2008; Bonomi et al., 2009; Bonomi and Parrinello, 2010; Dama et al., 2014) using a single PHD and head group mimic of the PI(4,5)P₂ (IP₃: inositol triphosphate). We set up three different systems for WT-MTD simulations: two systems where the distance collective variables (CVs) are chosen such that the variable loops are sampled preferentially and another system with no bias for any loop or pocket. CVs can be thought of as reaction coordinates or order parameters that can distinguish between different conformational states of the PIP₂-PHD complex in this work. The schematic of CV selection is shown in the left panel of Figure 8, and the corresponding free energy surface (FES) profiles are shown in the right panel. The details of CV definition are discussed in the Supplemental Information. The convergence plot for the three systems and the time evolution of distance in and out of the ligand from the domain’s pocket are shown in Supplemental Figure S6. To explore whether a variety of binding geometries exist, we considered the geometries in the range of ∼2 k_BT of the deepest minima. We observed a range of possible geometries suggesting degeneracy, which implies that PIP₂, or rather the IP₃ ligand, can bind with different sets of residues in the PHD. Results from IP₃-PHD simulations show that pockets formed by VL1-VL3 and VL1-VL4 are both available for binding the inositol head group.

FIGURE 8:

Well-tempered metadynamics setup with docking region for IP₃ (ligand) biased toward the VL1 and VL3 loop region (A1), toward the VL1 and VL4 loop region (B1), and with no bias toward any loop region (C1). The free energy landscapes for the three systems are shown in panels A2, B2, and C2, respectively. The lowest energy configurations are picked from the lowest basin and region free energy difference of <2k_BT from the minimum basin.

It should be noted that the WT-MTD runs were carried out with an isolated lipid head group (IP₃), and so we wanted to check how well the information from these runs would relate back to membrane interaction modes of the PHD. To address this issue as well as to gain further insights into the configurations of binding geometry of bilayer-bound PHD, we performed the following simulation. We extracted the coordinates of PHD-IP₃ from the deepest basins of free energy landscapes obtained from the WT-MTD runs. The first set of coordinates were obtained from WT-MTD data where the IP₃ was positioned in the pocket between the VL1 and VL4 loops. The other set of coordinates was taken from simulations where the IP₃ was positioned in the pocket between the VL1 and VL3 loops. The coordinates were superimposed onto the membrane bilayer (DOPC:DOPS:PIP₂ in 80:19:1 ratio), making sure that the orientation of PHD-IP₃ remained unchanged. This was done by aligning the IP₃ ligand with the head group of PIP₂, the membrane with only rotational and translational modes allowed during superimposition. The prescription is similar to what was done with the electron paramagnetic resonance-based structure of IP₃-PHD of GRP1 to simulate a bilayer-bound PHD (Chen et al., 2012; Lai et al., 2013). We then let the system evolve in an all-atom NPT ensemble simulation for 500 ns each. This allowed us to test the stability of the configurations obtained from IP₃-PHD WT-MTD runs in the presence of bilayer. We find that the simulation initiated from the orientation taken from minima obtained in the region of loops 1–3 is unstable compared with the orientation observed in the minima obtained from the loop 1–4 system. Please see Figure 9A, where the root-mean-square deviation (RMSD) is plotted keeping the first frame (configuration from converged WT-MTD runs) as the reference indicating that the VL1-VL4 basin configuration is robust. We chose this system for further analysis to look into residues that consistently engage with the acyl-chain hydrocarbon core as well as into residues that have nontransient interactions with PIP₂ lipid and explore whether any of the interactions localizes the anionic PS lipids and stabilizes the interactions further.

FIGURE 9:

(A) RMSD plot of AAMD runs for two systems, one started with PIP₂ docking derived from a metadynamics run with IP₃ ligand in VL1-VL3 and the other with IP₃ ligand in the VL1-VL4 pocket. The latter shows stable convergence and was chosen for 500 ns of the MD simulation, where we explored the lipid contacts of the PHD. (B) One of the last snapshots of the MD run (water and ions not shown). PC lipids are shown in gray, PS in green, and PIP₂ lipid in red. The PHD is shown in a transparent white isosurf representation, and VL1, VL3, and VL4 are shown in opaque blue, red, and orange, respectively. The full movie file of this trajectory is also reported in Supplemental Movie-AA. (C–F) Normalized contacts that different kinds of lipids make with residues on various loops.

In Figure 9B, we show a snapshot at the end of the 500 ns, which shows the lipid engagements of various loops. Contact analysis of our trajectories shows that lipid tail atoms consistently interact with residues I533 and M534 of VL1 (Figure 9C), indicating hydrophobic association of the VL1 loop. However, what we find very interesting is how the PHD is stabilized further using residues such as K535 and K359 that recruit PS lipids near the VL1. This is quite evident in the Supplemental Movie-AA. VL1 accesses the hydrophobic core in a nonspecific manner, but once the PS lipids and PIP₂ are recruited to the location, the I533 and M534 residue stabilize PS and PIP₂ in its place by making contact with its tail. It is also amply clear from our HMMM simulations (see Supplemental Movie-HMMM) and AAMD simulations (see Supplemental Movie-AA) that VL3 has vital interactions with PIP₂. HMMM runs show that the PIP₂ is locked to the binding pocket once it makes contact with the polar VL3. AAMD analyses also highlight how PIP₂ is localized without VL3 partitioning into the membrane. A plot of the z-distance of the C-alpha and z-distance of the terminal “hydroxyl oxygen” atom of Y600 as a function of time reveals nominal association with the membrane. While Y600L mutation is tried and tested for fission inhibition behavior, our results indicate R594 and R601 as critical residues on VL3 (Figure 9D) involved in interaction with PIP₂. This could be tested experimentally to provide further insights into dynamin’s membrane association mechanisms. While VL1 and VL3 loops have been studied in depth for more than a decade now (and VL2 is not important for membrane association but shows some role in PS recruitment; Figure 9E through K554), no study has so far looked into the role of VL4. A clinical observation of a large family of Charcot–Marie–Tooth patients with the Met580Thr mutation supports the importance of this loop (Haberlová et al., 2011). On the other hand, in a hydrogen/deuterium exchange(HDX)-mass spectroscopy–based study, Srinivasan et al. (2016), explored the accessibility of dynamin residues upon nucleotide and/or membrane binding. Unlike our findings, they did not see any detectable change in protection of VL4 associated peptides, which can be misinterpreted as an absence of membrane association for VL4. It should be noted that the membrane accessibility of a given residue was reported based on the difference in solvent exchange behaviors of the residue in the membrane-bound state of dynamin1 with that of its apo state (existing as a dimer or tetramer in solution). It is possible that VL4 residues may be inaccessible to solvent in the apo state owing to its existence as dimers/tetramers in solution. In that case, the membrane-bound state and the apo state of the residue will show no difference in solvent exchange, which may likely reconcile the inconsistency with our results that clearly shows that VL4 is membrane bound. From our analyses, we show that VL4 consistently partitions into the hydrophobic core of the membrane though the association seems facile given that we see only marginal loss in binding free energies with mutations on VL4 residues. However, mutations such as F579A and K583A have very noticeable effects on the orientation stability of the PHD on the membrane despite no visible loss in membrane partitioning. Figure 9D clearly shows the heavy contacts that F579 and M580 and other residues of VL4 make with the membrane. Our observations can inform experiments to test the role played by VL4 in terms of orientation stability of PHD.

Conclusions

The dynamin collar undergoes a series of segmental rearrangements while executing membrane fission. Each PHD must be capable of adapting to the progressively remodeled underlying membrane. Previous results from three-dimensional (3D) reconstructions of dynamin mutants trapped in a constricted state (Chappie et al., 2011; Sundborger et al., 2014; Kong et al., 2018) as well as data from biochemical and multiple fluorescence spectroscopic approaches (Mehrotra et al., 2014) suggest that the PHD can associate with the membrane in different orientations. Theoretical analyses of determinants that could lower the energy barrier for fission have invoked tilting of the PHD to conform with the evolving membrane curvature and thereby creating a low-energy pathway for fission (Shnyrova et al., 2013; Pannuzzo et al., 2018; Kadosh et al., 2019). Our multiscale simulations data validate these possibilities and provide molecular insights in terms of effects of PHD on membrane properties and lipid conformations and on the binding geometries and orientation stability of PHD on membrane, all of which may affect processes downstream of membrane binding.

We show that binding of the PHDs lowers the membrane-bending rigidity, indicating that molecular interactions at the membrane interface confer a change in the bending rigidity of the membrane. These changes are brought about by polar and charged residues at the membrane interface that locally reduce membrane thickness and increase chain flexibility. Recent evidence of the existence of nonbilayer configurations of lipids formed at the stalk and hemifission intermediates prompted us to go beyond models that assume the membrane as an elastic sheet capable of undergoing fission through curvature instability (Leibler, 1986; Kozlov, 2001; Kooijman et al., 2003; Liu et al., 2011; Frolov et al., 2015; Fuhrmans and Müller, 2015) and focus on the molecular degrees of freedom of constituent lipids. Thus, higher fluctuations in the lipid tilt and lipid tail splay may have a significant role in facilitating the membrane to stochastically cross-over to the nonbilayer intermediates once a threshold constriction of the lumen is reached. The formation of nonbilayer intermediates dictates that a physical coupling between the two leaflets of the bilayer is reduced (Shchelokovskyy et al., 2011). However, our analysis reveals no apparent change in the interdigitation between the two leaflets, and this could reflect the fact that our simulations are currently not designed to recapitulate dynamics of the constricted tubular intermediate seen during fission.

With growing structural, biochemical, and modeling evidence supporting the role for PHD–lipid interactions, it is important to put our results into the context of the two prevalent models for the dynamin-induced fission mechanism (Antonny et al., 2016). The mechanochemical (constriction/ratchet) model and the catalytic activities (constriction/stochastic–cross-over) model may not be mutually exclusive and could together constitute the underlying fission mechanism. This aspect is very elegantly presented in the contribution from Frolov and Bashkirov in a recently published topical review (Bassereau et al., 2018). In our work, through molecular-scale modeling we also try to clearly bring out the catalytic aspect of PHD, and our work provides molecular insights into how the various variable loops may mediate membrane association, assembly, membrane mechanical properties, and prefission lipid conformations. The role of membrane rigidity in dynamin-mediated fission is established firmly by experiments (Morlot et al., 2012; Pinot et al., 2014), and our data on the role of PHDs in inducing local curvatures and enhanced membrane fluctuations (reducing rigidity) lend further credence to the mechanism that proposes stochastic cross-over to fission once the constriction reaches a reversible hemifission state (Shnyrova et al., 2013; Mehrotra et al., 2014; Frolov et al., 2015; Mattila et al., 2015; Dar and Pucadyil, 2017; Zhang and Müller, 2017). The mechanochemical constrictase/ratchet model for fission (Chappie et al., 2010, 2011; Faelber et al., 2011; Ford et al., 2011; Reubold et al., 2015) treats dynamin as a pure GTP-driven motor protein that triggers sliding of the helical turn, leading to membrane constriction and eventual fission. The stalk domain in dynamin, which mediates dimerization/assembly as well the power-stroke sliding motion, is connected to the activity-providing GTPase on the one end and to the membrane-associating PHD on the other end. The x-ray diffraction–derived structural data on dynamin constructs (Chappie et al., 2011; Faelber et al., 2011; Reubold et al., 2015) provide a strong basis for the existence of the above-mentioned model. However, for the stalk domain in particular, which is central to this mechanism, the structural data do not reconcile with the later cryo-EM data (Sundborger et al., 2014; Kong et al., 2018). This inconsistency could be due to the possible conformational rearrangements in the stalk domain, particularly during the membrane-bound assembly process. If that is the case, for the stalk domain to function effectively in the proposed mechanism, the role of PHDs as a highly regulated flexible pivot further comes to the fore and may be used to further reconcile the two prevalent proposed mechanisms in the literature.

The PHD is a ubiquitous membrane-binding domain for many different proteins. Several studies have explored the molecular mechanism by which it associates with PIP₂/PIP₃ in the membrane (Lai et al., 2013; Srivastava and Voth, 2014; Jian et al., 2015; Vonkova et al., 2015; Naughton et al., 2016, 2018; Yamamoto et al., 2016; Chan et al., 2017; Pant and Tajkhorshid, 2020; Soubias et al., 2020). Analysis of inositol-bound PHD structures clearly reveals the presence of a highly basic region that favors binding to the highly anionic phosphoinositide lipids (Ferguson et al., 1995; Lemmon et al., 1995). Our results from AAMD, WT-MTD, and HMMM runs extend these models and provide molecular-level insights into dyn-PHD engagement with membrane. Our simulation studies show that membrane binding of dyn-PHD has features that are quite unique. In general, multiple binding site studies suggest a mechanism with canonical and atypical phosphoinositide-binding sites that allows efficient switching between active and inactive forms in proteins (Jian et al., 2015; Yamamoto et al., 2016, 2020; Soubias et al., 2020). There is an important difference between the degeneracy in binding sites in our work as compared with that observed in other systems including ASAP1-PHD. Residues from multiple variable loops engage with the same PIP₂ lipid in the case of dyn-PHD. The “catalytic” role of dyn-PHD is evident in our work due to its role in lowering the barrier to fission. Multiple binding loops around a PIP₂ may explain how the dyn-PHD is able to “dynamically” keep itself anchored to the membrane while undergoing very rapid shape changes in the midst of the fission process.

Despite the fact that all three VLs appear to engage with the membrane, albeit to different extents and through different modes, the degeneracy in orientations lends credence to the notion that unlike being rigidly clamped to the membrane, the PHDs are best represented as units that are flexible and “moored” to the membrane. VL1 acts as a primary anchor that dictates the binding affinity with the membrane, a feature driven by both hydrophobic interactions (I533A showing reduced dissociation free energy) and stabilization by recruitment of PS lipids at VL1 by residues such as K535 and K539 on the loop. Interestingly, residue K554 on VL2 seems to also favor PS lipid recruitment to the PHD, though VL2 is quite distant from the membrane surface. VL3, a highly polar loop, never partitions with the bilayer but is instrumental in localizing PIP₂. Given that the protruded head group of PIP₂ allows such interactions, it would be interesting to see how mutations on VL3 residues behave in membranes with different curvatures and anionic lipid composition. VL4 has a subtler role in dictating the orientation flexibility of dyn-PHD, and we provide some testable hypotheses toward that end. None of the experimental studies has probed the role of VL4 in PHD–membrane interaction, possibly because the center of the loop is rich in hydrophobic residues with distal lysines unlike VL1 and VL3 (Lemmon and Ferguson, 2000), where the positively charged residues are at the tip of the loop. Our study identifies this novel interaction between VL4 and the membrane and highlights its role as an auxiliary pivot providing orientation stability to the PHD—a feature that we believe is important for effective polymerization of the dynamin collar. Our findings with respect to both multiple binding sites (Jian et al., 2015; Soubias et al., 2020; Yamamoto et al., 2020) and multiple orientations (Shnyrova et al., 2013; Mehrotra et al., 2014) have to be reexamined in the light of the auxiliary pivot theory. Put together, our results indicate that the membrane binding and orientation stability is tightly regulated by concerted interactions among three different loops on the dyn-PHD, which acts as a flexible pivot and modulates effective and expedited fission.

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Complete descriptions of the all-atom simulation parameters, metadynamics simulation parameters, and umbrella sampling simulations as well as the details of Martini and HMMM CG modeling are provided below or are available in the Supplemental Information. Moreover, all input files, including starting coordinates of the various systems, required to run all the simulation jobs for all methods, areavailable on the Github platform (https://github.com/codesrivastavalab/dynPHD).

CG simulations

Two CG bilayer systems with and without dyn1-PHDs (randomly oriented) were generated using the Martini bilayer builder in the CHARMM-GUI online server (Jo et al., 2008). The lipid bilayer was composed of 2048 lipids with a composition of DOPC-DOPS-PIP₂ (80:19:1). These systems were simulated in the NPT (constant number of particles, pressure and temperature) ensemble using the MARTINI Polarizable force field (Version 2.2P) in GROMACS (Marrink et al., 2004, 2007; Monticelli et al., 2008). Both these systems were minimized using a steepest descent algorithm followed by an equilibration of 5–10 ns before proceeding to a 4 μs production run at 310 K temperature and 1 atm pressure. The temperature and pressure were maintained at 310 K and 1 atm using the V-rescale thermostat and Berendsen barostat (with semiisotropic coupling scheme), respectively. To understand the influence of dyn1-PHD on the mechanical properties of the lipid bilayer, we estimated the BM of the lipid bilayer with and without dyn1-PHDs. In this regard we adopted the reciprocal space-based method of Brandt et al. (2011) to obtain membrane undulation fluctuation spectra. The spectra so obtained were used to extract the BM using the Helfrich theory. To evaluate the mean and SD on the BM estimate, we performed the spectra evaluation on the full trajectory as well as on blocks of 1 μs of the full trajectory. The reported values were evaluated from the estimates from individual blocks. All the relevant data files, Python script, and c++ codes can be found at the Github location https://github.com/codesrivastavalab/dynPHD/.

Curvature analysis

Curvature analysis was performed on martini CG patches with and without PHDomains using the following protocol. The coordinates of phosphate head groups of lipids corresponding to one of the leaflets were extracted. A 2D Delaunay triangulation algorithm was then employed to generate a polygonal mesh of vertices from the coordinates of phosphate head groups. The surface, so generated, was used for evaluating the mean and gaussian curvature at various vertices of the mesh. These calculations were performed using Python scripts coupled with built-in subroutines from the VTK (Visualization ToolKit) library (Schroeder et al., 2004) which is used in Memsurfer to perform curvature calculations (Bhatia et al., 2019).The results were visualized using Paraview (Ahrens et al., 2005; Bethel et al., 2012) and its plugins.

HMMM simulations

HMMM simulations (Ohkubo et al., 2012; Vermaas and Tajkhorshid, 2014a) were performed using GROMACS with the CHARMM36 protein force field (Huang et al., 2017) and CHARMM36 phospholipid force field (Klauda et al., 2010) with a time step of 2 fs. We ran 12 different replicates with starkly different initial orientations of PHD, and each system was run for a minimum of 500 ns. The membrane was composed of a 80:19:1 mixture of DOPC, DOPS and POPI head groups (100 lipid molecules per leaflet). The core of the bilayer was made of DCLE molecules (∼1200). The bilayer–PHD systems were solvated and ionized with 150 mM NaCl using VMD (Visual Molecular Dynamics) (Humphrey et al., 1996). For each system, the following simulation protocol was used: the system was well equilibrated in both NVT (constant number of particles, volume and temperature) and NPT ensemble for 20 ns prior setting up for production run. Nonbonded forces were calculated with a 12 Å cutoff (10 Å: switching distance). Long-range electrostatic forces were calculated at every other time step using the particle mesh Ewald method (Essmann et al., 1995). The system is maintained at a temperature of 310 K and pressure of 1 atm using a Nose–Hoover thermostat and Parrinello–Rahman (with semi-isotropic coupling) barostat with time constants 1.0 and 5.0 ps^–1, respectively.

All-atom simulations

We performed a series of AAMD NPT-simulations on WT and mutant dyn-PHD with membrane using GROMACS (Table 1) to understand the dynamics and to obtain deeper molecular insights into the dyn1-PHD on the membrane surface. Each of these systems was energy minimized and equilibrated for 20 ns. Each system comprises PHD, ∼200 lipids, ∼23,000 water molecules, and 150 mM NaCl. The CHARMM36 force field (Klauda et al., 2010) was used for particle definitions. Analysis of thickness variation across the membrane surface and protein was carried out using Python-based FATSLiM (Buchoux, 2017). The lipid conformational analysis was carried out using an in-house VMD TCL script or the VMD membrane plug-in tool (Guixà-González et al., 2014).

TABLE 1:

WT and mutant PHDs used for all-atom membrane simulations with membrane composition of DOPC-DOPS-PIP₂ (80:19:1).

Membrane + PHD variant	Simulation time (ns)
Wild type	500
I533A	500
F579A	500
K539A	500
K583A	500
Y600L	500
I533A-F579A	500
F579K-K583A	500
F579A-S581K	500
K539A-K583A	500

Cryo-EM analysis

The cryo-EM map (Kong et al., 2018) for the constricted collar (K44A mutant) of dynamin (EMD-2701) was obtained from the EM databank (https://www.emdataresource.org/EMD-2701). The map was visualized using chimera (Pettersen et al., 2004) and was colored according to the cylinder radius. An in-house R code (R Core Team, 2020) was used to calculate the distribution of angles taken by PHDs in the cryo-EM map. Our code is available on the aforementioned Github repository.

Protein–ligand metadynamics

The structure of dyn1-PHD (protein) was obtained from the protein data bank (1DYN) (Ferguson et al., 1994). The force-field parameters of inositol triphosphate (ligand) corresponding to the CHARMM force field were generated using the Swissparam server (Zoete et al., 2011). The initial configurations of the protein–ligand system were constructed in cubic box using PYMOL (Schrödinger, 2015). The systems were then solvated with TIP3P water molecules and neutralized using 150 mM NaCl. All the systems were energy minimized and equilibrated to a temperature of 310 K and 1 atm pressure before proceeding to production runs. The velocity rescaling algorithm (Bussi et al., 2007) (time constant of 0.1 ps) and Parrinello–Rahman algorithm (Parrinello and Rahman, 1981) (time constant of 2 ps) were used to maintain temperature and pressure, respectively. Bond constraints were dealt using LINCS algorithm (Hess, 2008). The long-range electrostatic interactions were dealt using a particle mesh Ewald scheme with order 4 and a Fourier spacing of 0.16 while the short-range interactions were dealt using a Verlet scheme with a cutoff of 1.4 nm. All the simulations were performed in GROMACS (Abraham et al., 2015) patched with PLUMED-2.3.5 (Tribello et al., 2014). Short production runs of 10 ns were performed before proceeding for metadynamics runs. The details of different systems and the definitions of their respective CVs can be found in the Supplemental Information as well as in the input files shared on the Github repository.

Umbrella sampling simulations

The initial coordinates for setting up the umbrella sampling simulation were taken from the last frame of the corresponding PHD(WT/mutant)–lipid all-atom trajectory at the end of 500 ns runs. To get the umbrella locations, we placed PHD away from the membrane surface and saved the coordinates of the system at every 1 Å window up to a distance of 25 Å. The systems were then ionized and solvated for AAMD runs. The coordinates thus obtained were used as initial configurations for the 25 windows that constitute umbrella sampling simulations. Here, we chose the distance between the center of masses of the protein and the membrane to be restrained as the window centers (with restraint constant k = 1000 kJ/mol/nm²). Each window was simulated for 50 ns of the production run with the umbrella restraint turned on preceded by an equilibration run. The PMF profile was then calculated using gmx wham tool. The error along the PMF profile was obtained by performing a bootstrap analysis with 100 bootstraps. All profiles were shifted to maintain the PMF value at the membrane plane at 0 kcal/mol value for reference. The same protocol was used for generating the PMF profiles of all the systems of interest.

Abbreviations used:

AAMD

all-atom molecular dynamics

BM

bending modulus

CG

coarse-grained

CV

collective variable

DOPC

1,2-dioleoyl- sn-glycero-3-phosphocholine

DOPS

1,2-dioleoyl- sn-glycero-3-phospho- l-serine

HMMM

highly mobile membrane-mimetic model

PHD

pleckstrin homology domain

PIP ₂

phosphatidylinositol-4,5-bisphosphate

PMF

potential of mean force

VL

variable loop

WT-MTD

well-tempered metadynamics

WT

wild-type.