Figure 8. Probabilistic graphical model of the proposed forward model.

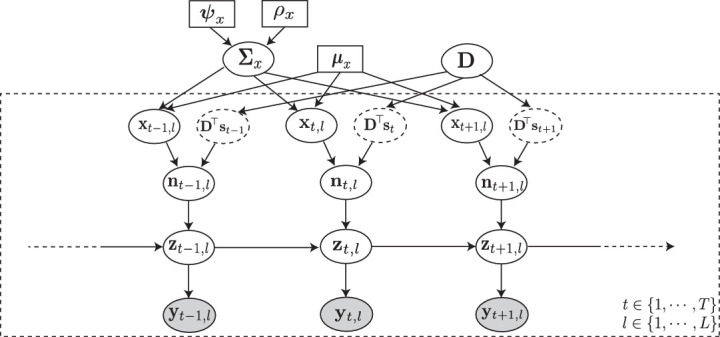
The fluorescence observations at the $t^{\mathrm{𝗍𝗁}}$ time frame and $l^{\mathrm{𝗍𝗁}}$ trial: ${\mathbf{𝐲}}_{t,l}$, are noisy surrogates of the intracellular calcium concentrations: ${\mathbf{𝐳}}_{t,l}$. The calcium concentration at time $t$ is a function of the spiking activity ${\mathbf{𝐧}}_{t,l}$, and the calcium activity at the previous time point ${\mathbf{𝐳}}_{t-1,l}$. The spiking activity is driven by two independent mechanisms: latent trial-dependent covariates ${\mathbf{𝐱}}_{t,l}$, and contributions from the known external stimulus ${\mathbf{𝐬}}_t$, which we model by ${\mathbf{𝐃}}^{\top }{\mathbf{𝐬}}_t$ (in which the receptive field $\mathbf{𝐃}$ is unknown). Then, we model ${\mathbf{𝐱}}_{t,l}$ as a Gaussian process with constant mean ${\mathit{𝝁}}_x$, and unknown covariance ${\mathbf{𝚺}}_x$. Finally, we assume the covariance ${\mathbf{𝚺}}_x$ to have an inverse Wishart prior distribution with hyper-parameters ${\displaystyle {\mathit{\psi }}_x}$ and ${\rho }_x$. Based on this forward model, the inverse problem amounts to recovering the signal and noise correlations by directly estimating ${\mathbf{𝚺}}_x$ and $\mathbf{𝐃}$ (top layer) from the fluorescence observations ${\left\{{\mathbf{𝐲}}_{t,l}\right\}}_{t=1,l=1}^{T,L}$ (bottom layer).